Estructura de banda electrónica

En física del estado sólido , la estructura de banda electrónica (o simplemente estructura de banda ) de un sólido describe el rango de niveles de energía que los electrones pueden tener dentro de él, así como los rangos de energía que pueden no tener (llamados intervalos de banda o bandas prohibidas ).

La teoría de bandas obtiene estas bandas y brechas de banda examinando las funciones de onda mecánicas cuánticas permitidas para un electrón en una red grande y periódica de átomos o moléculas. La teoría de bandas se ha utilizado con éxito para explicar muchas propiedades físicas de los sólidos, como la resistividad eléctrica y la absorción óptica , y constituye la base de la comprensión de todos los dispositivos de estado sólido (transistores, células solares, etc.).

¿Por qué se producen bandas y brechas de banda?

Animación de la formación de bandas y cómo los electrones las llenan en un metal y un aislante.

La formación de bandas electrónicas y brechas de banda se puede ilustrar con dos modelos complementarios para electrones en sólidos. ^[1]^{: 161} El primero es el modelo de electrones casi libres , en el que se supone que los electrones se mueven casi libremente dentro del material. En este modelo, los estados electrónicos se asemejan a ondas planas de electrones libres y solo se ven ligeramente perturbados por la red cristalina. Este modelo explica el origen de la relación de dispersión electrónica, pero la explicación de las brechas de banda es sutil en este modelo. ^[2]^{: 121}

El segundo modelo parte del límite opuesto, en el que los electrones están fuertemente ligados a átomos individuales. Los electrones de un solo átomo aislado ocupan orbitales atómicos con niveles de energía discretos . Si dos átomos se acercan lo suficiente como para que sus orbitales atómicos se superpongan, los electrones pueden hacer un túnel entre los átomos. Este túnel divide ( hibrida ) los orbitales atómicos en orbitales moleculares con diferentes energías. ^[2]^{: 117–122}

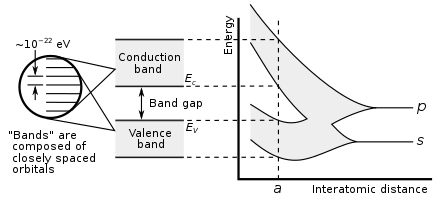
De manera similar, si una gran cantidad $N$ de átomos idénticos se juntan para formar un sólido, como una red cristalina , los orbitales atómicos de los átomos se superponen con los orbitales cercanos. ^[3] Cada nivel de energía discreto se divide en $N$ niveles, cada uno con una energía diferente. Dado que el número de átomos en una pieza macroscópica de sólido es un número muy grande ( $N$ ≈ 10 ²² ), el número de orbitales que se hibridan entre sí es muy grande. Por esta razón, los niveles adyacentes están muy espaciados en energía (del orden de10 ⁻²² eV ), ^[4]^[5]^[6] y pueden considerarse que forman un continuo, una banda de energía.

Esta formación de bandas es una característica principalmente de los electrones más externos ( electrones de valencia ) del átomo, que son los que participan en la unión química y la conductividad eléctrica . Los orbitales electrónicos internos no se superponen en un grado significativo, por lo que sus bandas son muy estrechas.

Los intervalos de banda son esencialmente rangos de energía sobrantes que no están cubiertos por ninguna banda, como resultado de los anchos finitos de las bandas de energía. Las bandas tienen diferentes anchos, que dependen del grado de superposición en los orbitales atómicos de los que surgen. Es posible que dos bandas adyacentes simplemente no sean lo suficientemente anchas para cubrir por completo el rango de energía. Por ejemplo, las bandas asociadas con los orbitales centrales (como los electrones 1s ) son extremadamente estrechas debido a la pequeña superposición entre átomos adyacentes. Como resultado, tiende a haber grandes intervalos de banda entre las bandas centrales. Las bandas más altas involucran orbitales comparativamente más grandes con más superposición, volviéndose progresivamente más anchas a energías más altas, de modo que no hay intervalos de banda a energías más altas.

Conceptos básicos

Supuestos y límites de la teoría de la estructura de bandas

La teoría de bandas es sólo una aproximación al estado cuántico de un sólido, que se aplica a los sólidos que constan de muchos átomos o moléculas idénticos unidos entre sí. Estos son los supuestos necesarios para que la teoría de bandas sea válida:

Sistema de tamaño infinito : para que las bandas sean continuas, el trozo de material debe estar formado por una gran cantidad de átomos. Dado que un trozo macroscópico de material contiene del orden de 10 ^{22 átomos, esto no supone una restricción importante; la teoría de bandas se aplica incluso a}transistores de tamaño microscópico en circuitos integrados . Con modificaciones, el concepto de estructura de bandas también se puede extender a sistemas que sólo son "grandes" en algunas dimensiones, como los sistemas electrónicos bidimensionales .
Sistema homogéneo : La estructura de bandas es una propiedad intrínseca de un material, que supone que el material es homogéneo. En la práctica, esto significa que la composición química del material debe ser uniforme en toda la pieza.
No interactividad : La estructura de bandas describe "estados de un solo electrón". La existencia de estos estados supone que los electrones se desplazan en un potencial estático sin interactuar dinámicamente con vibraciones reticulares , otros electrones, fotones , etc.

Las suposiciones anteriores no se cumplen en una serie de situaciones prácticas importantes, y el uso de la estructura de bandas requiere que se controlen de cerca las limitaciones de la teoría de bandas:

Inhomogeneidades e interfaces: Cerca de superficies, uniones y otras inhomogeneidades, la estructura de banda en masa se ve alterada. No solo hay alteraciones locales a pequeña escala (por ejemplo, estados de superficie o estados dopantes dentro del intervalo de banda), sino también desequilibrios de carga locales. Estos desequilibrios de carga tienen efectos electrostáticos que se extienden profundamente a semiconductores, aislantes y el vacío (ver dopaje , flexión de banda ).
En la misma línea, la mayoría de los efectos electrónicos ( capacidad , conductancia eléctrica , apantallamiento del campo eléctrico ) involucran la física de los electrones que pasan a través de superficies y/o cerca de interfaces. La descripción completa de estos efectos, en una imagen de la estructura de bandas, requiere al menos un modelo rudimentario de interacciones electrón-electrón (ver carga espacial , flexión de bandas ).
Sistemas pequeños: En el caso de sistemas que son pequeños en todas sus dimensiones (por ejemplo, una molécula pequeña o un punto cuántico ), no existe una estructura de banda continua. El cruce entre dimensiones pequeñas y grandes es el ámbito de la física mesoscópica .
Los materiales fuertemente correlacionados (por ejemplo, los aislantes de Mott ) simplemente no pueden entenderse en términos de estados de un solo electrón. Las estructuras de bandas electrónicas de estos materiales están mal definidas (o al menos, no están definidas de manera única) y pueden no brindar información útil sobre su estado físico.

Simetría cristalina y vectores de onda

Fig. 2. Diagrama de estructura de bandas para Si , Ge , GaAs e InAs generado con un modelo de enlace fuerte. Nótese que Si y Ge son materiales de banda prohibida indirecta, mientras que GaAs e InAs son directos.

Los cálculos de la estructura de bandas aprovechan la naturaleza periódica de una red cristalina, explotando su simetría. La ecuación de Schrödinger de un solo electrón se resuelve para un electrón en un potencial periódico de red, dando como soluciones los electrones de Bloch , donde $k$ se denomina vector de onda. Para cada valor de $k$ , existen múltiples soluciones a la ecuación de Schrödinger etiquetadas por $n$ , el índice de banda, que simplemente numera las bandas de energía. Cada uno de estos niveles de energía evoluciona suavemente con los cambios en $k$ , formando una banda suave de estados. Para cada banda podemos definir una función $E$ $n$ $($ $k$ $)$ , que es la relación de dispersión para los electrones en esa banda. $\psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} ),$

El vector de onda toma cualquier valor dentro de la zona de Brillouin , que es un poliedro en el espacio de vectores de onda ( red recíproca ) que está relacionado con la red del cristal. Los vectores de onda fuera de la zona de Brillouin simplemente corresponden a estados que son físicamente idénticos a aquellos estados dentro de la zona de Brillouin. A los puntos/líneas especiales de alta simetría en la zona de Brillouin se les asignan etiquetas como Γ, Δ, Λ, Σ (ver Figura 1).

Es difícil visualizar la forma de una banda como una función del vector de onda, ya que requeriría un gráfico en el espacio de cuatro dimensiones, $E$ vs. $k x$ , $k y$ , $k z$ . En la literatura científica es común ver gráficos de estructura de banda que muestran los valores de $E n (k)$ para valores de $k$ a lo largo de líneas rectas que conectan puntos de simetría, a menudo etiquetados como Δ, Λ, Σ o [100], [111] y [110] , respectivamente. ^[7]^[8] Otro método para visualizar la estructura de banda es trazar una isosuperficie de energía constante en el espacio del vector de onda, mostrando todos los estados con energía igual a un valor particular. La isosuperficie de los estados con energía igual al nivel de Fermi se conoce como superficie de Fermi .

Las bandas de energía prohibidas se pueden clasificar utilizando los vectores de onda de los estados que rodean la banda prohibida:

Banda prohibida directa : el estado de menor energía por encima de la banda prohibida tiene el mismo $k$ que el estado de mayor energía por debajo de la banda prohibida.
Banda prohibida indirecta : los estados más cercanos por encima y por debajo de la banda prohibida no tienen el mismo valor $k .$

Asimetría: Estructuras de bandas en sólidos no cristalinos

Aunque las estructuras de bandas electrónicas suelen asociarse a materiales cristalinos , los sólidos cuasicristalinos y amorfos también pueden presentar brechas de banda. Estas son algo más difíciles de estudiar teóricamente, ya que carecen de la simetría simple de un cristal y, por lo general, no es posible determinar una relación de dispersión precisa. Como resultado, prácticamente todo el trabajo teórico existente sobre la estructura de bandas electrónicas de los sólidos se ha centrado en materiales cristalinos.

Densidad de estados

La función de densidad de estados $g (E)$ se define como el número de estados electrónicos por unidad de volumen, por unidad de energía, para energías de electrones cercanas a $E$ .

La función de densidad de estados es importante para los cálculos de efectos basados en la teoría de bandas. En la regla de oro de Fermi , un cálculo para la tasa de absorción óptica , proporciona tanto el número de electrones excitables como el número de estados finales para un electrón. Aparece en los cálculos de conductividad eléctrica donde proporciona el número de estados móviles, y en el cálculo de las tasas de dispersión de electrones donde proporciona el número de estados finales después de la dispersión. ^{[ cita requerida ]}

Para energías dentro de un intervalo de banda, $g (E) = 0$ .

Relleno de bandas

En el equilibrio termodinámico , la probabilidad de que un estado de energía $E$ esté ocupado por un electrón viene dada por la distribución de Fermi-Dirac , una distribución termodinámica que tiene en cuenta el principio de exclusión de Pauli : donde: $f(E)={\frac {1}{1+e^{{(E-\mu )}/{k_{\text{B}}T}}}}$

$k B T$ es el producto de la constante de Boltzmann y la temperatura , y
$µ$ es el potencial químico total de los electrones, o nivel de Fermi (en física de semiconductores , esta cantidad se suele denotar $como E F$ ). El nivel de Fermi de un sólido está directamente relacionado con el voltaje en ese sólido, medido con un voltímetro. Convencionalmente, en los gráficos de estructura de bandas, el nivel de Fermi se toma como el cero de energía (una elección arbitraria).

La densidad de electrones en el material es simplemente la integral de la distribución de Fermi-Dirac por la densidad de estados: $N/V=\int _{-\infty }^{\infty }g(E)f(E)\,dE$

Aunque hay un número infinito de bandas y, por lo tanto, un número infinito de estados, solo hay un número finito de electrones para colocar en estas bandas. El valor preferido para el número de electrones es una consecuencia de la electrostática: aunque la superficie de un material puede cargarse, la masa interna de un material prefiere ser neutral en cuanto a carga. La condición de neutralidad de carga significa que $N / V$ debe coincidir con la densidad de protones en el material. Para que esto ocurra, el material se ajusta electrostáticamente, desplazando su estructura de bandas hacia arriba o hacia abajo en energía (desplazando así $g (E)$ ), hasta que está en el equilibrio correcto con respecto al nivel de Fermi.

Nombres de bandas cercanas al nivel de Fermi (banda de conducción, banda de valencia)

Un sólido tiene un número infinito de bandas permitidas, al igual que un átomo tiene infinitos niveles de energía. Sin embargo, la mayoría de las bandas simplemente tienen una energía demasiado alta y, por lo general, se descartan en circunstancias normales. ^[9] Por el contrario, existen bandas de energía muy baja asociadas con los orbitales centrales (como los electrones 1s ). Estas bandas centrales de baja energía también suelen descartarse, ya que permanecen llenas de electrones en todo momento y, por lo tanto, son inertes. ^[10] Asimismo, los materiales tienen varias brechas de banda a lo largo de su estructura de bandas.

Las bandas y los intervalos de banda más importantes (aquellos que son relevantes para la electrónica y la optoelectrónica) son aquellos con energías cercanas al nivel de Fermi. Las bandas y los intervalos de banda cercanos al nivel de Fermi reciben nombres especiales, según el material:

En un semiconductor o aislante de banda , el nivel de Fermi está rodeado por una brecha de banda, denominada banda prohibida (para distinguirla de las otras brechas de banda en la estructura de banda). La banda más cercana por encima de la brecha de banda se llama banda de conducción , y la banda más cercana por debajo de la brecha de banda se llama banda de valencia . El nombre "banda de valencia" fue acuñado por analogía con la química, ya que en semiconductores (y aislantes) la banda de valencia está formada por los orbitales de valencia .
En un metal o semimetal , el nivel de Fermi está dentro de una o más bandas permitidas. En los semimetales, las bandas suelen denominarse "banda de conducción" o "banda de valencia" según si el transporte de carga es más parecido al de los electrones o al de los huecos, por analogía con los semiconductores. Sin embargo, en muchos metales, las bandas no son ni parecidas a los electrones ni a los huecos, y a menudo se las llama simplemente "banda de valencia", ya que están formadas por orbitales de valencia. ^[11] Los huecos de banda en la estructura de bandas de un metal no son importantes para la física de baja energía, ya que están demasiado lejos del nivel de Fermi.

Teoría en cristales

El ansatz es el caso especial de las ondas electrónicas en una red cristalina periódica utilizando el teorema de Bloch tal como se trata de manera general en la teoría dinámica de la difracción . Cada cristal es una estructura periódica que puede caracterizarse por una red de Bravais , y para cada red de Bravais podemos determinar la red recíproca , que encapsula la periodicidad en un conjunto de tres vectores de red recíprocos $(b 1, b 2, b 3)$ . Ahora, cualquier potencial periódico $V (r)$ que comparte la misma periodicidad que la red directa puede expandirse como una serie de Fourier cuyos únicos componentes no nulos son aquellos asociados con los vectores de red recíprocos. Por lo tanto, la expansión puede escribirse como: donde $K$ $=$ $m$ $1$ $b$ $1$ $+$ $m$ $2$ $b$ $2$ $+$ $m$ $3$ $b$ $3$ para cualquier conjunto de números enteros $($ $m$ $1$ $,$ $m$ $2$ $,$ $m$ $3$ $)$ . $V(\mathbf {r} )=\sum _{\mathbf {K} }{V_{\mathbf {K} }e^{i\mathbf {K} \cdot \mathbf {r} }}$

A partir de esta teoría, se puede intentar predecir la estructura de bandas de un material particular, sin embargo la mayoría de los métodos ab initio para cálculos de estructura electrónica no logran predecir la banda prohibida observada.

Aproximación de electrones casi libres

En la aproximación del electrón casi libre, las interacciones entre electrones se ignoran por completo. Esta aproximación permite el uso del teorema de Bloch , que establece que los electrones en un potencial periódico tienen funciones de onda y energías que son periódicas en el vector de onda hasta un desfase constante entre vectores reticulares recíprocos vecinos . Las consecuencias de la periodicidad se describen matemáticamente mediante el teorema de Bloch, que establece que las funciones de onda de los estados propios tienen la forma donde la función de Bloch es periódica sobre la red cristalina, es decir, $\Psi _{n,\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n}(\mathbf {r} )$ $u_{n}(\mathbf {r} )$ $u_{n}(\mathbf {r} )=u_{n}(\mathbf {r} -\mathbf {R} ).$

Aquí el índice $n$ se refiere a la banda de energía $n , el vector de onda$ $k$ está relacionado con la dirección del movimiento del electrón, $r$ es la posición en el cristal y $R$ es la ubicación de un sitio atómico. ^[12]^{: 179}

El modelo NFE funciona particularmente bien en materiales como los metales, donde las distancias entre átomos vecinos son pequeñas. En tales materiales, la superposición de orbitales atómicos y potenciales en átomos vecinos es relativamente grande. En ese caso, la función de onda del electrón puede aproximarse mediante una onda plana (modificada). La estructura de bandas de un metal como el aluminio incluso se acerca a la aproximación de red vacía .

Modelo de encuadernación estrecha

El extremo opuesto a la aproximación de electrones casi libres supone que los electrones en el cristal se comportan de forma muy similar a un conjunto de átomos constituyentes. Este modelo de enlace estrecho supone que la solución a la ecuación de Schrödinger de un solo electrón independiente del tiempo se aproxima bien mediante una combinación lineal de orbitales atómicos . ^[12]^{: 245–248} donde los coeficientes se seleccionan para dar la mejor solución aproximada de esta forma. El índice $n$ se refiere a un nivel de energía atómica y $R$ se refiere a un sitio atómico. Un enfoque más preciso que utiliza esta idea emplea funciones de Wannier , definidas por: ^[12]^{: Eq. 42 p. 267}^[13] en la que es la parte periódica del teorema de Bloch y la integral es sobre la zona de Brillouin . Aquí el índice $n$ se refiere a la banda de energía $n$ -ésima en el cristal. Las funciones de Wannier se localizan cerca de los sitios atómicos, como los orbitales atómicos, pero al estar definidas en términos de funciones de Bloch se relacionan con precisión con soluciones basadas en el potencial del cristal. Las funciones de Wannier en diferentes sitios atómicos $R$ son ortogonales. 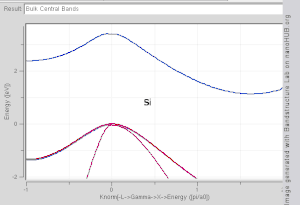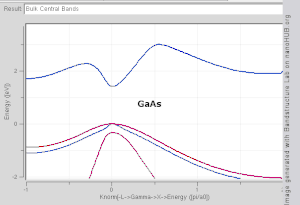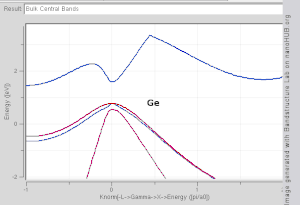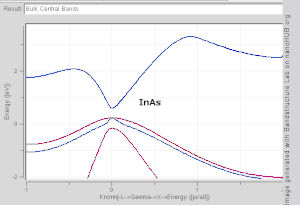Las funciones de Wannier se pueden utilizar para formar la solución de Schrödinger para la banda de energía $n -ésima como:$ $\Psi$ $\psi _{n}(\mathbf {r} )$ $\Psi (\mathbf {r} )=\sum _{n,\mathbf {R} }b_{n,\mathbf {R} }\psi _{n}(\mathbf {r} -\mathbf {R} ),$ $b_{n,\mathbf {R} }$ $a_{n}(\mathbf {r} -\mathbf {R} )={\frac {V_{C}}{(2\pi )^{3}}}\int _{\text{BZ}}d\mathbf {k} e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}u_{n\mathbf {k} };$ $u_{n\mathbf {k} }$ $\Psi _{n,\mathbf {k} }(\mathbf {r} )=\sum _{\mathbf {R} }e^{-i\mathbf {k} \cdot (\mathbf {R} -\mathbf {r} )}a_{n}(\mathbf {r} -\mathbf {R} ).$

El modelo TB funciona bien en materiales con una superposición limitada entre los orbitales atómicos y los potenciales de los átomos vecinos. Las estructuras de bandas de materiales como Si , GaAs , SiO ₂ y el diamante , por ejemplo, están bien descritas por los hamiltonianos TB sobre la base de los orbitales atómicos sp ³ . En los metales de transición, se utiliza un modelo TB-NFE mixto para describir la amplia banda de conducción NFE y las estrechas bandas d TB incrustadas. Las funciones radiales de la parte orbital atómica de las funciones de Wannier se calculan más fácilmente mediante el uso de métodos pseudopotenciales . Los cálculos de estructura de banda NFE, TB o combinados NFE-TB, ^[14] a veces ampliados con aproximaciones de función de onda basadas en métodos pseudopotenciales, se utilizan a menudo como un punto de partida económico para cálculos posteriores.

Modelo KKR

El método KKR, también llamado "teoría de dispersión múltiple" o método de la función de Green, encuentra los valores estacionarios de la matriz de transición inversa T en lugar del hamiltoniano. Korringa , Kohn y Rostocker sugirieron una implementación variacional, y a menudo se la conoce como el método de Korringa-Kohn-Rostoker . ^[15]^[16] Las características más importantes de la formulación de KKR o función de Green son (1) que separa los dos aspectos del problema: la estructura (posiciones de los átomos) de la dispersión (identidad química de los átomos); y (2) las funciones de Green proporcionan un enfoque natural para una descripción localizada de las propiedades electrónicas que se puede adaptar a aleaciones y otros sistemas desordenados. La forma más simple de esta aproximación centra esferas no superpuestas (conocidas como moldes para muffins ) en las posiciones atómicas. Dentro de estas regiones, el potencial experimentado por un electrón se aproxima a ser esféricamente simétrico alrededor del núcleo dado. En la región intersticial restante, el potencial apantallado se aproxima como una constante. Se garantiza la continuidad del potencial entre las esferas centradas en los átomos y la región intersticial.

Teoría funcional de la densidad

En la literatura de física reciente, una gran mayoría de las estructuras electrónicas y los gráficos de bandas se calculan utilizando la teoría funcional de la densidad (DFT), que no es un modelo sino más bien una teoría, es decir, una teoría microscópica de primeros principios de la física de la materia condensada que intenta abordar el problema de muchos cuerpos electrón-electrón mediante la introducción de un término de correlación de intercambio en el funcional de la densidad electrónica . En muchos casos, se ha descubierto que las bandas calculadas mediante DFT concuerdan con las bandas medidas experimentalmente, por ejemplo, mediante espectroscopia de fotoemisión con resolución angular (ARPES). En particular, la forma de la banda suele reproducirse bien mediante DFT. Pero también hay errores sistemáticos en las bandas de DFT cuando se comparan con los resultados experimentales. En particular, la DFT parece subestimar sistemáticamente en aproximadamente un 30-40% la brecha de banda en aislantes y semiconductores. ^[17]

Se cree comúnmente que la DFT es una teoría para predecir las propiedades del estado fundamental de un sistema únicamente (por ejemplo, la energía total , la estructura atómica , etc.), y que las propiedades del estado excitado no se pueden determinar mediante la DFT. Esto es un concepto erróneo. En principio, la DFT puede determinar cualquier propiedad (estado fundamental o estado excitado) de un sistema dado un funcional que mapea la densidad del estado fundamental a esa propiedad. Esta es la esencia del teorema de Hohenberg-Kohn. ^[18] En la práctica, sin embargo, no existe ningún funcional conocido que mapee la densidad del estado fundamental a las energías de excitación de los electrones dentro de un material. Por lo tanto, lo que en la literatura se cita como un diagrama de bandas de la DFT es una representación de las energías de Kohn-Sham de la DFT , es decir, las energías de un sistema ficticio que no interactúa, el sistema Kohn-Sham, que no tiene interpretación física alguna. La estructura electrónica de Kohn-Sham no debe confundirse con la estructura electrónica real de cuasipartículas de un sistema, y no existe un teorema de Koopmans válido para las energías de Kohn-Sham, como sí lo hay para las energías de Hartree-Fock, que puede considerarse verdaderamente como una aproximación para las energías de cuasipartículas. Por lo tanto, en principio, la DFT basada en Kohn-Sham no es una teoría de bandas, es decir, no es una teoría adecuada para calcular bandas y diagramas de bandas. En principio, la DFT dependiente del tiempo se puede utilizar para calcular la verdadera estructura de bandas, aunque en la práctica esto suele ser difícil. Un enfoque popular es el uso de funcionales híbridos , que incorporan una parte del intercambio exacto de Hartree-Fock; esto produce una mejora sustancial en las brechas de banda previstas de los semiconductores, pero es menos confiable para metales y materiales de brecha de banda ancha. ^[19]

Los métodos de función de Green y ladesde el principioAproximación de GW

Para calcular las bandas que incluyen los efectos de muchos cuerpos de la interacción electrón-electrón , se puede recurrir a los llamados métodos de la función de Green . De hecho, el conocimiento de la función de Green de un sistema proporciona tanto los observables de base (la energía total) como los del estado excitado del sistema. Los polos de la función de Green son las energías de las cuasipartículas, las bandas de un sólido. La función de Green se puede calcular resolviendo la ecuación de Dyson una vez que se conoce la autoenergía del sistema. Para sistemas reales como los sólidos, la autoenergía es una cantidad muy compleja y, por lo general, se necesitan aproximaciones para resolver el problema. Una de estas aproximaciones es la aproximación GW , llamada así por la forma matemática que toma la autoenergía como el producto Σ = GW de la función de Green G y la interacción filtrada dinámicamente W. Este enfoque es más pertinente cuando se aborda el cálculo de gráficos de bandas (y también de cantidades más allá, como la función espectral) y también se puede formular de una manera completamente ab initio . La aproximación GW parece proporcionar brechas de banda de aislantes y semiconductores de acuerdo con el experimento y, por lo tanto, corregir la subestimación sistemática de DFT.

Teoría del campo medio dinámico

Aunque la aproximación del electrón casi libre es capaz de describir muchas propiedades de las estructuras de bandas de electrones, una consecuencia de esta teoría es que predice el mismo número de electrones en cada celda unitaria. Si el número de electrones es impar, entonces esperaríamos que haya un electrón desapareado en cada celda unitaria y, por lo tanto, que la banda de valencia no esté completamente ocupada, lo que hace que el material sea un conductor. Sin embargo, los materiales como CoO que tienen un número impar de electrones por celda unitaria son aislantes, en conflicto directo con este resultado. Este tipo de material se conoce como aislante de Mott y requiere la inclusión de interacciones electrón-electrón detalladas (tratadas solo como un efecto promedio sobre el potencial cristalino en la teoría de bandas) para explicar la discrepancia. El modelo de Hubbard es una teoría aproximada que puede incluir estas interacciones. Puede tratarse de forma no perturbativa dentro de la llamada teoría del campo medio dinámico , que intenta salvar la brecha entre la aproximación del electrón casi libre y el límite atómico. Sin embargo, formalmente en este caso los estados no dejan de interactuar y el concepto de estructura de banda no es adecuado para describir estos casos.

Otros

El cálculo de estructuras de bandas es un tema importante en la física teórica del estado sólido . Además de los modelos mencionados anteriormente, otros modelos incluyen los siguientes:

Aproximación de red vacía : la "estructura de banda" de una región de espacio libre que se ha dividido en una red.
La teoría de perturbación k·p es una técnica que permite describir aproximadamente una estructura de bandas en términos de unos pocos parámetros. La técnica se utiliza habitualmente para semiconductores y los parámetros del modelo suelen determinarse experimentalmente.
El modelo de Kronig-Penney , un modelo de pozo rectangular unidimensional útil para ilustrar la formación de bandas. Si bien es simple, predice muchos fenómenos importantes, pero no es cuantitativo.
Modelo de Hubbard

La estructura de banda se ha generalizado a vectores de onda que son números complejos , dando como resultado lo que se denomina una estructura de banda compleja , que es de interés en superficies e interfaces.

Cada modelo describe muy bien algunos tipos de sólidos y mal otros. El modelo de electrones casi libres funciona bien para metales, pero mal para no metales. El modelo de enlace fuerte es extremadamente preciso para aislantes iónicos, como sales de haluro metálico (p. ej. NaCl ).

Diagramas de bandas

Para entender cómo cambia la estructura de bandas en relación con el nivel de Fermi en el espacio real, un gráfico de estructura de bandas se simplifica primero en forma de diagrama de bandas . En un diagrama de bandas, el eje vertical es la energía, mientras que el eje horizontal representa el espacio real. Las líneas horizontales representan los niveles de energía, mientras que los bloques representan las bandas de energía. Cuando las líneas horizontales en estos diagramas están inclinadas, la energía del nivel o banda cambia con la distancia. En forma de diagrama, esto representa la presencia de un campo eléctrico dentro del sistema cristalino. Los diagramas de bandas son útiles para relacionar las propiedades generales de la estructura de bandas de diferentes materiales entre sí cuando se colocan en contacto entre sí.

Véase también

Ingeniería de banda prohibida : el proceso de alterar la estructura de banda de un material
Felix Bloch – pionero en la teoría de la estructura de bandas
Alan Herries Wilson – pionero en la teoría de la estructura de bandas

Referencias

^ Simon, Steven H. (2013). Fundamentos del estado sólido de Oxford. Oxford: Oxford University Press. ISBN 978-0-19-150210-1.
^ de Girvin, Steven M.; Yang, Kun (2019). Física moderna de la materia condensada . Cambridge: Cambridge University Press. ISBN 978-1-107-13739-4.
^ Holgate, Sharon Ann (2009). Comprensión de la física del estado sólido. CRC Press. pp. 177–178. ISBN 978-1-4200-1232-3.
^ Halliday, David; Resnick, Robert; Walker, Jearl (2013). Fundamentos de física, versión ampliada, 10.ª edición. John Wiley and Sons. pág. 1254. ISBN 9781118230619.
^ Cai, Wenshan; Shalaev, Vladimir (2009). Metamateriales ópticos: fundamentos y aplicaciones. Springer Science and Business Media. pág. 12. ISBN 9781441911513.
^ Ibach, Harald; Lüth, Hans (2009). Física del estado sólido: Introducción a los principios de la ciencia de los materiales, 4.ª edición. Springer Science and Business Media. pág. 2. ISBN 9783540938040.
^ "Archivo NSM - Arseniuro de galio y aluminio (AlGaAs) - Estructura de bandas y concentración de portadores". www.ioffe.ru .
^ "Estructura de banda electrónica" (PDF) . www.springer.com . Springer. p. 24 . Consultado el 10 de noviembre de 2016 .
^ Las bandas de alta energía son importantes para la física de difracción de electrones , donde los electrones pueden inyectarse en un material a altas energías, véase Stern, R.; Perry, J.; Boudreaux, D. (1969). "Superficies de dispersión de difracción de electrones de baja energía y estructura de bandas en reflexiones mixtas tridimensionales de Laue y Bragg". Reseñas de Física Moderna . 41 (2): 275. Bibcode :1969RvMP...41..275S. doi :10.1103/RevModPhys.41.275..
^ Sin embargo, las bandas de baja energía son importantes en el efecto Auger .
^ En el cobre, por ejemplo, la masa efectiva es un tensor y también cambia de signo dependiendo del vector de onda, como se puede ver en el efecto De Haas-Van Alphen ; véase https://www.phys.ufl.edu/fermisurface/
^ abc Charles Kittel (1996). Introducción a la física del estado sólido (séptima edición). Nueva York: Wiley. ISBN 978-0-471-11181-8.
^ Daniel Charles Mattis (1994). El problema de los muchos cuerpos: enciclopedia de modelos resueltos con exactitud en una dimensión. World Scientific. pág. 340. ISBN 978-981-02-1476-0.
^ Walter Ashley Harrison (1989). Estructura electrónica y propiedades de los sólidos. Publicaciones de Dover. ISBN 978-0-486-66021-9.
^ Joginder Singh Galsin (2001). Dispersión de impurezas en aleaciones metálicas. Springer. Apéndice C. ISBN 978-0-306-46574-1.
^ Kuon Inoue, Kazuo Ohtaka (2004). Cristales fotónicos. Springer. pág. 66. ISBN 978-3-540-20559-3.
^ Assadi, M. Hussein. N.; Hanaor, Dorian AH (21 de junio de 2013). "Estudio teórico sobre la energética y el magnetismo del cobre en polimorfos de TiO _{2 ".}Journal of Applied Physics . 113 (23): 233913–233913–5. arXiv : 1304.1854 . Bibcode :2013JAP...113w3913A. doi :10.1063/1.4811539. ISSN 0021-8979. S2CID 94599250.
^ Hohenberg, P; Kohn, W. (noviembre de 1964). "Gas de electrones no homogéneo". Phys. Rev. 136 ( 3B): B864–B871. Código Bibliográfico :1964PhRv..136..864H. doi : 10.1103/PhysRev.136.B864 .
^ Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, IC; Angyán, JG (2006). "Funcionales de densidad híbridos seleccionados aplicados a sólidos". J Chem Phys . 124 (15): 154709. Bibcode :2006JChPh.124o4709P. doi :10.1063/1.2187006. PMID 16674253.

Lectura adicional

Ashcroft, Neil y N. David Mermin, Física del estado sólido , ISBN 0-03-083993-9
Harrison, Walter A., Estructura electrónica elemental , ISBN 981-238-708-0
Harrison, Walter A.; WA Benjamin Pseudopotenciales en la teoría de los metales , (Nueva York) 1966
Marder, Michael P., Física de la materia condensada , ISBN 0-471-17779-2
Martin, Richard, Estructura electrónica: teoría básica y métodos prácticos , ISBN 0-521-78285-6
Millman, Jacob; Arvin Gabriel, Microelectrónica , ISBN 0-07-463736-3 , Edición Tata McGraw-Hill.
Nemoshkalenko, VV, y NV Antonov, Métodos computacionales en física del estado sólido , ISBN 90-5699-094-2
Omar, M. Ali, Física elemental del estado sólido: principios y aplicaciones , ISBN 0-201-60733-6
Singh, Jasprit, Propiedades electrónicas y optoelectrónicas de estructuras semiconductoras, capítulos 2 y 3, ISBN 0-521-82379-X
Vasileska, Dragica , Tutorial sobre métodos de estructura de bandas (2008)