Mecánica de fracturas

Estudio de la propagación de grietas en materiales

Las cargas en la punta de una grieta se pueden reducir a una combinación de tres factores de intensidad de tensión independientes.

La mecánica de fracturas es el campo de la mecánica que se ocupa del estudio de la propagación de grietas en los materiales. Utiliza métodos de mecánica analítica de sólidos para calcular la fuerza impulsora de una grieta y métodos de mecánica experimental de sólidos para caracterizar la resistencia del material a la fractura .

En teoría, la tensión que se encuentra delante de la punta de una grieta afilada se vuelve infinita y no se puede utilizar para describir el estado alrededor de una grieta. La mecánica de fracturas se utiliza para caracterizar las cargas en una grieta, normalmente utilizando un único parámetro para describir el estado de carga completo en la punta de la grieta. Se han desarrollado varios parámetros diferentes. Cuando la zona plástica en la punta de la grieta es pequeña en relación con la longitud de la grieta, el estado de tensión en la punta de la grieta es el resultado de fuerzas elásticas dentro del material y se denomina mecánica de fractura elástica lineal ( LEFM ) y se puede caracterizar utilizando el factor de intensidad de tensión . Aunque la carga en una grieta puede ser arbitraria, en 1957 G. Irwin descubrió que cualquier estado podía reducirse a una combinación de tres factores de intensidad de tensión independientes: ${\displaystyle K}$

• Modo I – Modo de apertura (una tensión de tracción normal al plano de la grieta),
• Modo II – Modo deslizante (una tensión cortante que actúa paralela al plano de la grieta y perpendicular al frente de la grieta), y
• Modo III – Modo de desgarro (una tensión cortante que actúa paralela al plano de la grieta y paralela al frente de la grieta).

Cuando el tamaño de la zona plástica en la punta de la grieta es demasiado grande, se puede utilizar la mecánica de fractura elastoplástica con parámetros como la integral J o el desplazamiento de apertura de la punta de la grieta .

El parámetro de caracterización describe el estado de la punta de la grieta, que luego se puede relacionar con las condiciones experimentales para garantizar la similitud . El crecimiento de la grieta ocurre cuando los parámetros generalmente exceden ciertos valores críticos. La corrosión puede hacer que una grieta crezca lentamente cuando se excede el umbral de intensidad de la tensión de corrosión bajo tensión . De manera similar, pequeños defectos pueden provocar el crecimiento de la grieta cuando se someten a una carga cíclica. Conocida como fatiga , se encontró que para grietas largas, la tasa de crecimiento está regida en gran medida por el rango de la intensidad de la tensión experimentada por la grieta debido a la carga aplicada. La fractura rápida ocurrirá cuando la intensidad de la tensión exceda la tenacidad a la fractura del material. La predicción del crecimiento de la grieta es el núcleo de la disciplina de diseño mecánico de tolerancia al daño . ${\displaystyle \Delta K}$

Motivación

Los procesos de fabricación, procesamiento, mecanizado y conformado de materiales pueden introducir defectos en un componente mecánico terminado. Los defectos interiores y superficiales que surgen del proceso de fabricación se encuentran en todas las estructuras metálicas. No todos estos defectos son inestables en condiciones de servicio. La mecánica de fracturas es el análisis de los defectos para descubrir aquellos que son seguros (es decir, que no crecen) y aquellos que son propensos a propagarse como grietas y, por lo tanto, causar el fallo de la estructura defectuosa. A pesar de estos defectos inherentes, es posible lograr mediante el análisis de tolerancia al daño el funcionamiento seguro de una estructura. La mecánica de fracturas como tema de estudio crítico apenas existe desde hace un siglo y, por lo tanto, es relativamente nueva. ^{[1] [2]}

La mecánica de fracturas debería intentar proporcionar respuestas cuantitativas a las siguientes preguntas: ^[2]

1. ¿Cuál es la resistencia del componente en función del tamaño de la grieta?
2. ¿Qué tamaño de grieta se puede tolerar bajo carga de servicio, es decir, cuál es el tamaño de grieta máximo permitido?
3. ¿Cuánto tiempo tarda una grieta en crecer desde un tamaño inicial determinado, por ejemplo el tamaño de grieta mínimo detectable, hasta el tamaño de grieta máximo permitido?
4. ¿Cuál es la vida útil de una estructura cuando se supone que existe un cierto tamaño de defecto preexistente (por ejemplo, un defecto de fabricación)?
5. Durante el período disponible para la detección de grietas, ¿con qué frecuencia se debe inspeccionar la estructura para detectar grietas?

Mecánica de fractura elástica lineal

El criterio de Griffith

Una grieta (defecto) de Griffith de longitud está en el medio ^{[3] [4]} un material infinitamente grande ${\displaystyle a}$

La mecánica de fracturas fue desarrollada durante la Primera Guerra Mundial por el ingeniero aeronáutico inglés A. A. Griffith (de ahí el término grieta de Griffith ) para explicar la falla de materiales frágiles. ^[5] El trabajo de Griffith estuvo motivado por dos hechos contradictorios:

• La tensión necesaria para fracturar el vidrio a granel es de alrededor de 100 MPa (15.000 psi).
• La tensión teórica necesaria para romper los enlaces atómicos del vidrio es de aproximadamente 10.000 MPa (1.500.000 psi).

Se necesitaba una teoría para conciliar estas observaciones contradictorias. Además, los experimentos con fibras de vidrio que el propio Griffith llevó a cabo sugirieron que la tensión de fractura aumenta a medida que disminuye el diámetro de la fibra. Por lo tanto, la resistencia a la tracción uniaxial, que se había utilizado ampliamente para predecir la falla del material antes de Griffith, no podía ser una propiedad del material independiente de la muestra. Griffith sugirió que la baja resistencia a la fractura observada en los experimentos, así como la dependencia del tamaño de la resistencia, se debía a la presencia de fallas microscópicas en el material en masa.

Para verificar la hipótesis del defecto, Griffith introdujo un defecto artificial en sus muestras de vidrio experimentales. El defecto artificial tenía la forma de una grieta superficial mucho más grande que otros defectos en una muestra. Los experimentos demostraron que el producto de la raíz cuadrada de la longitud del defecto ( ) y la tensión en la fractura ( ) era casi constante, lo que se expresa mediante la ecuación: ${\displaystyle a}$ ${\displaystyle \sigma _{f}}$

${\displaystyle \sigma _{f}{\sqrt {a}}\approx C}$

Explicar esta relación en términos de la teoría de la elasticidad lineal es problemático. La teoría de la elasticidad lineal predice que la tensión (y, por lo tanto, la deformación) en la punta de una falla aguda en un material elástico lineal es infinita. Para evitar ese problema, Griffith desarrolló un enfoque termodinámico para explicar la relación que observó.

El crecimiento de una grieta, la extensión de las superficies a ambos lados de la grieta, requiere un aumento de la energía superficial . Griffith encontró una expresión para la constante en términos de la energía superficial de la grieta al resolver el problema de elasticidad de una grieta finita en una placa elástica. Brevemente, el enfoque fue: ${\displaystyle C}$

• Calcular la energía potencial almacenada en una muestra perfecta bajo una carga de tracción uniaxial.
• Fije el límite de modo que la carga aplicada no realice ningún trabajo y luego introduzca una grieta en la muestra. La grieta relaja la tensión y, por lo tanto, reduce la energía elástica cerca de las caras de la grieta. Por otro lado, la grieta aumenta la energía superficial total de la muestra.
• Calcular el cambio en la energía libre (energía superficial − energía elástica) en función de la longitud de la grieta. La falla ocurre cuando la energía libre alcanza un valor máximo en una longitud de grieta crítica, más allá de la cual la energía libre disminuye a medida que aumenta la longitud de la grieta, es decir, al provocar la fractura. Usando este procedimiento, Griffith descubrió que

${\displaystyle C={\sqrt {\cfrac {2E\gamma }{\pi }}}}$

donde es el módulo de Young del material y es la densidad de energía superficial del material. Suponiendo y se obtiene una excelente concordancia de la tensión de fractura predicha por Griffith con los resultados experimentales para el vidrio. ${\displaystyle E}$ ${\displaystyle \gamma }$ ${\displaystyle E=62\ {\text{GPa}}}$ ${\displaystyle \gamma =1\ {\text{J/m}}^{2}}$

Para el caso simple de una placa rectangular delgada con una grieta perpendicular a la carga, la tasa de liberación de energía, , se convierte en: ${\displaystyle G}$

${\displaystyle G={\frac {\pi \sigma ^{2}a}{E}}\,}$

donde es la tensión aplicada, es la mitad de la longitud de la grieta y es el módulo de Young , que para el caso de deformación plana debe dividirse por el factor de rigidez de la placa . La tasa de liberación de energía de deformación se puede entender físicamente como: la tasa a la que la energía es absorbida por el crecimiento de la grieta . ${\displaystyle \sigma }$ ${\displaystyle a}$ ${\displaystyle E}$ ${\displaystyle (1-\nu ^{2})}$

Sin embargo, también tenemos que:

${\displaystyle G_{c}={\frac {\pi \sigma _{f}^{2}a}{E}}\,}$

Si ≥ , este es el criterio por el cual la grieta comenzará a propagarse. ${\displaystyle G}$ ${\displaystyle G_{c}}$

Para materiales altamente deformados antes de la propagación de la grieta, la formulación de mecánica de fractura elástica lineal ya no es aplicable y es necesario un modelo adaptado para describir el campo de tensión y desplazamiento cerca de la punta de la grieta, como en la fractura de materiales blandos .

Modificación de Irwin

La zona plástica alrededor de la punta de una grieta en un material dúctil

El trabajo de Griffith fue en gran medida ignorado por la comunidad de ingeniería hasta principios de la década de 1950. Las razones para esto parecen ser (a) en los materiales estructurales reales, el nivel de energía necesario para causar una fractura es órdenes de magnitud mayor que la energía superficial correspondiente, y (b) en los materiales estructurales siempre hay algunas deformaciones inelásticas alrededor del frente de la grieta que harían que la suposición de un medio elástico lineal con tensiones infinitas en la punta de la grieta sea altamente irreal. ^[6]

La teoría de Griffith proporciona una excelente concordancia con los datos experimentales para materiales frágiles como el vidrio. Para materiales dúctiles como el acero , aunque la relación todavía se mantiene, la energía superficial ( γ ) predicha por la teoría de Griffith suele ser irrealmente alta. Un grupo que trabajaba bajo la dirección de GR Irwin ^[7] en el Laboratorio de Investigación Naval de los EE. UU. (NRL) durante la Segunda Guerra Mundial se dio cuenta de que la plasticidad debe desempeñar un papel importante en la fractura de materiales dúctiles. ${\displaystyle \sigma _{f}{\sqrt {a}}=C}$

En los materiales dúctiles (e incluso en los materiales que parecen frágiles ^[8] ), se desarrolla una zona plástica en la punta de la grieta. A medida que aumenta la carga aplicada , la zona plástica aumenta de tamaño hasta que la grieta crece y el material elásticamente deformado detrás de la punta de la grieta se descarga. El ciclo de carga y descarga plástica cerca de la punta de la grieta conduce a la disipación de energía en forma de calor . Por lo tanto, se debe agregar un término disipativo a la relación de balance de energía ideada por Griffith para materiales frágiles. En términos físicos, se necesita energía adicional para el crecimiento de la grieta en materiales dúctiles en comparación con materiales frágiles.

La estrategia de Irwin fue dividir la energía en dos partes:

• La energía de deformación elástica almacenada que se libera a medida que crece una grieta es la fuerza impulsora termodinámica de la fractura.
• La energía disipada, que incluye la disipación plástica y la energía superficial (y cualquier otra fuerza disipativa que pueda estar en juego). La energía disipada proporciona la resistencia termodinámica a la fractura.

Entonces la energía total es:

${\displaystyle G=2\gamma +G_{p}}$

donde es la energía superficial y es la disipación plástica (y la disipación de otras fuentes) por unidad de área de crecimiento de grietas. ${\displaystyle \gamma }$ ${\displaystyle G_{p}}$

La versión modificada del criterio de energía de Griffith puede entonces escribirse como

${\displaystyle \sigma _{f}{\sqrt {a}}={\sqrt {\cfrac {E~G}{\pi }}}.}$

Para materiales frágiles como el vidrio, predomina el término de energía superficial y . Para materiales dúctiles como el acero, predomina el término de disipación plástica y . Para polímeros cercanos a la temperatura de transición vítrea , tenemos valores intermedios de entre 2 y 1000 . ${\displaystyle G\approx 2\gamma =2\,\,{\text{J/m}}^{2}}$ ${\displaystyle G\approx G_{p}=1000\,\,{\text{J/m}}^{2}}$ ${\displaystyle G}$ ${\displaystyle {\text{J/m}}^{2}}$

Factor de intensidad del estrés

Otro logro significativo de Irwin y sus colegas fue encontrar un método para calcular la cantidad de energía disponible para la fractura en términos de los campos de tensión y desplazamiento asintóticos alrededor de un frente de grieta en un sólido elástico lineal. ^[7] Esta expresión asintótica para el campo de tensión en modo de carga I está relacionada con el siguiente factor de intensidad de tensión: ^[9] ${\displaystyle K_{I}}$

${\displaystyle \sigma _{ij}=\left({\cfrac {K_{I}}{\sqrt {2\pi r}}}\right)~f_{ij}(\theta )}$

donde son las tensiones de Cauchy , es la distancia desde la punta de la grieta, es el ángulo con respecto al plano de la grieta, y son funciones que dependen de la geometría de la grieta y de las condiciones de carga. Irwin llamó a la cantidad factor de intensidad de tensión. Dado que la cantidad es adimensional, el factor de intensidad de tensión se puede expresar en unidades de . ${\displaystyle \sigma _{ij}}$ ${\displaystyle r}$ ${\displaystyle \theta }$ ${\displaystyle f_{ij}}$ ${\displaystyle K}$ ${\displaystyle f_{ij}}$ ${\displaystyle {\text{MPa}}{\sqrt {\text{m}}}}$

La intensidad de la tensión sustituyó a la tasa de liberación de energía de deformación y un término llamado tenacidad a la fractura sustituyó a la energía de debilidad superficial. Ambos términos están simplemente relacionados con los términos de energía que utilizó Griffith:

${\displaystyle K_{I}=\sigma {\sqrt {\pi a}}\,}$

y

${\displaystyle K_{c}={\begin{cases}{\sqrt {EG_{c}}}&{\text{for plane stress}}\\\\{\sqrt {\cfrac {EG_{c}}{1-\nu ^{2}}}}&{\text{for plane strain}}\end{cases}}}$

donde es la intensidad del esfuerzo modal , la tenacidad a la fractura y es el coeficiente de Poisson. ${\displaystyle K_{I}}$ ${\displaystyle I}$ ${\displaystyle K_{c}}$ ${\displaystyle \nu }$

La fractura se produce cuando . Para el caso especial de la deformación por deformación plana, se convierte en y se considera una propiedad del material. El subíndice surge debido a las diferentes formas de cargar un material para permitir que se propague una grieta . Se refiere a la llamada carga "modal" en contraposición a la carga modal o : ${\displaystyle K_{I}\geq K_{c}}$ ${\displaystyle K_{c}}$ ${\displaystyle K_{Ic}}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle II}$ ${\displaystyle III}$

La expresión para será diferente para geometrías distintas a la placa infinita con grietas en el centro, como se analiza en el artículo sobre el factor de intensidad de tensión. En consecuencia, es necesario introducir un factor de corrección adimensional , , para caracterizar la geometría. Este factor de corrección, también denominado a menudo factor de forma geométrica , se da mediante series determinadas empíricamente y tiene en cuenta el tipo y la geometría de la grieta o entalla. Por lo tanto, tenemos: ${\displaystyle K_{I}}$ ${\displaystyle Y}$

${\displaystyle K_{I}=Y\sigma {\sqrt {\pi a}}\,}$

donde es una función de la longitud y el ancho de la grieta de la lámina dada, para una lámina de ancho finito que contiene una grieta a través del espesor de longitud , por: ${\displaystyle Y}$ ${\displaystyle W}$ ${\displaystyle 2a}$

${\displaystyle Y\left({\frac {a}{W}}\right)={\sqrt {\sec \left({\frac {\pi a}{W}}\right)}}\,}$

Liberación de energía de tensión

Irwin fue el primero en observar que si el tamaño de la zona plástica alrededor de una grieta es pequeño en comparación con el tamaño de la grieta, la energía requerida para hacer crecer la grieta no dependerá críticamente del estado de tensión (la zona plástica) en la punta de la grieta. ^[6] En otras palabras, se puede utilizar una solución puramente elástica para calcular la cantidad de energía disponible para la fractura.

La tasa de liberación de energía para el crecimiento de grietas o la tasa de liberación de energía de deformación se puede calcular entonces como el cambio en la energía de deformación elástica por unidad de área de crecimiento de grietas, es decir,

${\displaystyle G:=\left[{\cfrac {\partial U}{\partial a}}\right]_{P}=-\left[{\cfrac {\partial U}{\partial a}}\right]_{u}}$

donde U es la energía elástica del sistema y a es la longitud de la grieta. La carga P o el desplazamiento u son constantes al evaluar las expresiones anteriores.

Irwin demostró que para un modo de agrietamiento (modo de apertura), la tasa de liberación de energía de deformación y el factor de intensidad de tensión están relacionados por:

${\displaystyle G=G_{I}={\begin{cases}{\cfrac {K_{I}^{2}}{E}}&{\text{plane stress}}\\{\cfrac {(1-\nu ^{2})K_{I}^{2}}{E}}&{\text{plane strain}}\end{cases}}}$

donde E es el módulo de Young , ν es el coeficiente de Poisson y K _I es el factor de intensidad de tensión en el modo I. Irwin también demostró que la tasa de liberación de energía de deformación de una grieta plana en un cuerpo elástico lineal se puede expresar en términos de los factores de intensidad de tensión del modo I, modo II (modo de deslizamiento) y modo III (modo de desgarro) para las condiciones de carga más generales.

A continuación, Irwin adoptó la suposición adicional de que el tamaño y la forma de la zona de disipación de energía permanecen aproximadamente constantes durante la fractura frágil. Esta suposición sugiere que la energía necesaria para crear una superficie de fractura unitaria es una constante que depende únicamente del material. Esta nueva propiedad del material recibió el nombre de tenacidad a la fractura y se denominó G _Ic . Hoy en día, es el factor crítico de intensidad de tensión K _Ic , que se encuentra en la condición de deformación plana, el que se acepta como la propiedad definitoria en la mecánica de fractura elástica lineal.

Zona de plástico de la punta de la grieta

En teoría, la tensión en la punta de la grieta donde el radio es casi cero, tendería al infinito. Esto se consideraría una singularidad de tensión, lo cual no es posible en aplicaciones del mundo real. Por esta razón, en estudios numéricos en el campo de la mecánica de fracturas, a menudo es apropiado representar grietas como entalladuras con punta redondeada , con una región de concentración de tensión dependiente de la geometría que reemplaza la singularidad de la punta de la grieta. ^[9] En realidad, se ha encontrado que la concentración de tensión en la punta de una grieta dentro de materiales reales tiene un valor finito pero mayor que la tensión nominal aplicada a la muestra.

Sin embargo, debe haber algún tipo de mecanismo o propiedad del material que impida que una grieta de este tipo se propague espontáneamente. La suposición es que la deformación plástica en la punta de la grieta embota efectivamente la punta de la grieta. Esta deformación depende principalmente de la tensión aplicada en la dirección aplicable (en la mayoría de los casos, esta es la dirección y de un sistema de coordenadas cartesiano regular), la longitud de la grieta y la geometría de la muestra. ^[10] Para estimar cómo se extendía esta zona de deformación plástica desde la punta de la grieta, Irwin equiparó la resistencia a la fluencia del material a las tensiones de campo lejano de la dirección y a lo largo de la grieta (dirección x) y resolvió el radio efectivo. A partir de esta relación, y suponiendo que la grieta está cargada al factor de intensidad de tensión crítica, Irwin desarrolló la siguiente expresión para el radio idealizado de la zona de deformación plástica en la punta de la grieta:

${\displaystyle r_{p}={\frac {K_{C}^{2}}{2\pi \sigma _{Y}^{2}}}}$

Los modelos de materiales ideales han demostrado que esta zona de plasticidad está centrada en la punta de la grieta. ^[11] Esta ecuación proporciona el radio ideal aproximado de la deformación de la zona plástica más allá de la punta de la grieta, lo que es útil para muchos científicos estructurales porque da una buena estimación de cómo se comporta el material cuando se somete a tensión. En la ecuación anterior, los parámetros del factor de intensidad de tensión e indicador de tenacidad del material, , y la tensión de fluencia, , son importantes porque ilustran muchas cosas sobre el material y sus propiedades, así como sobre el tamaño de la zona plástica. Por ejemplo, si es alto, entonces se puede deducir que el material es tenaz, y si es bajo, uno sabe que el material es más dúctil. La relación de estos dos parámetros es importante para el radio de la zona plástica. Por ejemplo, si es pequeño, entonces la relación al cuadrado de a es grande, lo que resulta en un radio plástico mayor. Esto implica que el material puede deformarse plásticamente y, por lo tanto, es tenaz. ^[10] Esta estimación del tamaño de la zona plástica más allá de la punta de la grieta se puede utilizar luego para analizar con mayor precisión cómo se comportará un material en presencia de una grieta. ${\displaystyle K_{C}}$ ${\displaystyle \sigma _{Y}}$ ${\displaystyle K_{c}}$ ${\displaystyle \sigma _{Y}}$ ${\displaystyle \sigma _{Y}}$ ${\displaystyle K_{C}}$ ${\displaystyle \sigma _{Y}}$

El mismo proceso descrito anteriormente para una carga de un solo evento también se aplica a la carga cíclica. Si hay una grieta en una muestra que se somete a una carga cíclica, la muestra se deformará plásticamente en la punta de la grieta y retrasará el crecimiento de la grieta. En caso de una sobrecarga o excursión, este modelo cambia ligeramente para adaptarse al aumento repentino de la tensión con respecto a la que experimentó previamente el material. Con una carga suficientemente alta (sobrecarga), la grieta crece fuera de la zona plástica que la contenía y deja atrás el bolsillo de la deformación plástica original. Ahora, suponiendo que la tensión de sobrecarga no es lo suficientemente alta como para fracturar completamente la muestra, la grieta sufrirá una mayor deformación plástica alrededor de la nueva punta de la grieta, agrandando la zona de tensiones plásticas residuales. Este proceso endurece aún más y prolonga la vida del material porque la nueva zona plástica es más grande de lo que sería bajo las condiciones de tensión habituales. Esto permite que el material se someta a más ciclos de carga. Esta idea se puede ilustrar mejor con el gráfico del aluminio con una grieta central que sufre eventos de sobrecarga. ^[12]

Limitaciones

El SS Schenectady se partió en dos debido a una fractura frágil mientras estaba en el puerto, en 1943.

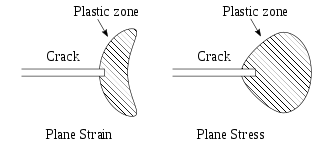
Pero surgió un problema para los investigadores del NRL porque los materiales navales, por ejemplo, las placas de acero para barcos, no son perfectamente elásticos, sino que sufren una deformación plástica significativa en la punta de una grieta. Un supuesto básico en la mecánica de fractura elástica lineal de Irwin es la fluencia a pequeña escala, la condición de que el tamaño de la zona plástica sea pequeño en comparación con la longitud de la grieta. Sin embargo, este supuesto es bastante restrictivo para ciertos tipos de fallas en aceros estructurales, aunque dichos aceros pueden ser propensos a la fractura frágil, lo que ha llevado a una serie de fallas catastróficas.

La mecánica de fractura elástica lineal tiene una utilidad práctica limitada para los aceros estructurales y las pruebas de tenacidad a la fractura pueden ser costosas.

Mecánica de fracturas elastoplásticas

Estabilizador vertical , que se desprendió del vuelo 587 de American Airlines , lo que provocó un accidente fatal

La mayoría de los materiales de ingeniería muestran un comportamiento elástico e inelástico no lineal en condiciones de funcionamiento que involucran grandes cargas. ^{[ cita requerida ]} En tales materiales, los supuestos de la mecánica de fractura elástica lineal pueden no ser válidos, es decir,

• La zona plástica en la punta de una grieta puede tener un tamaño del mismo orden de magnitud que el tamaño de la grieta.
• El tamaño y la forma de la zona plástica pueden cambiar a medida que aumenta la carga aplicada y también a medida que aumenta la longitud de la grieta.

Por lo tanto, se necesita una teoría más general del crecimiento de grietas para materiales elastoplásticos que pueda explicar:

• las condiciones locales para el crecimiento inicial de grietas, que incluyen la nucleación, el crecimiento y la coalescencia de huecos (descohesión) en la punta de una grieta.
• un criterio de balance energético global para un mayor crecimiento de grietas y fracturas inestables.

CTOD

Históricamente, el primer parámetro para la determinación de la tenacidad a la fractura en la región elasto-plástica era el desplazamiento de apertura de la punta de la grieta (CTOD) o “abertura en el ápice de la grieta” indicado. Este parámetro fue determinado por Wells durante los estudios de aceros estructurales, que debido a la alta tenacidad no podían caracterizarse con el modelo de mecánica de fractura elástica lineal. Observó que, antes de que ocurriera la fractura, las paredes de la grieta se iban desprendiendo ^{[ aclaración necesaria ]} y que la punta de la grieta, después de la fractura, variaba de aguda a redondeada debido a la deformación plástica. Además, el redondeo de la punta de la grieta era más pronunciado en aceros con tenacidad superior.

Existen varias definiciones alternativas de CTOD. En las dos definiciones más comunes, CTOD es el desplazamiento en la punta de la grieta original y la intersección de 90 grados. La última definición fue sugerida por Rice y se usa comúnmente para inferir CTOD en modelos de elementos finitos de este tipo. Tenga en cuenta que estas dos definiciones son equivalentes si la punta de la grieta se aplana en un semicírculo.

La mayoría de las mediciones de laboratorio de CTOD se han realizado en muestras con grietas en los bordes cargadas en flexión de tres puntos. Los primeros experimentos utilizaron un calibre plano en forma de paleta que se insertaba en la grieta; a medida que la grieta se abría, el calibre de paleta giraba y se enviaba una señal electrónica a un trazador xy. Sin embargo, este método era inexacto porque era difícil alcanzar la punta de la grieta con el calibre de paleta. Hoy en día, se mide el desplazamiento V en la boca de la grieta y el CTOD se infiere suponiendo que las mitades de la muestra son rígidas y giran alrededor de un punto de articulación (la punta de la grieta).

Curva R

Un primer intento en la dirección de la mecánica de fractura elastoplástica fue la curva de resistencia a la extensión de grietas de Irwin , la curva de resistencia al crecimiento de grietas o curva R. Esta curva reconoce el hecho de que la resistencia a la fractura aumenta con el aumento del tamaño de la grieta en materiales elastoplásticos. La curva R es un gráfico de la tasa de disipación de energía total en función del tamaño de la grieta y se puede utilizar para examinar los procesos de crecimiento lento y estable de grietas y fractura inestable. Sin embargo, la curva R no se utilizó ampliamente en aplicaciones hasta principios de la década de 1970. Las principales razones parecen ser que la curva R depende de la geometría de la muestra y la fuerza impulsora de la grieta puede ser difícil de calcular. ^[6]

J-integral

A mediados de la década de 1960, James R. Rice (en ese entonces en la Universidad Brown ) y GP Cherepanov desarrollaron de forma independiente una nueva medida de tenacidad para describir el caso en el que hay suficiente deformación en la punta de la grieta como para que la pieza ya no obedezca la aproximación elástica-lineal. El análisis de Rice, que supone una deformación elástica no lineal (o teoría de deformación monótona plástica ) por delante de la punta de la grieta, se designa como J-integral . ^[13] Este análisis se limita a situaciones en las que la deformación plástica en la punta de la grieta no se extiende hasta el borde más alejado de la pieza cargada. También exige que el comportamiento elástico no lineal asumido del material sea una aproximación razonable en forma y magnitud a la respuesta de carga del material real. El parámetro de falla elástica-plástica se designa J _Ic y se convierte convencionalmente a K _Ic utilizando la siguiente ecuación. Observe también que el enfoque de la J integral se reduce a la teoría de Griffith para el comportamiento elástico-lineal.

La definición matemática de la integral J es la siguiente:

${\displaystyle J=\int _{\Gamma }(w\,dy-T_{i}{\frac {\partial u_{i}}{\partial x}}\,ds)\quad {\text{with}}\quad w=\int _{0}^{\varepsilon _{ij}}\sigma _{ij}\,d\varepsilon _{ij}}$

dónde

${\displaystyle \Gamma }$es una trayectoria arbitraria en el sentido de las agujas del reloj alrededor del vértice de la grieta,

${\displaystyle w}$es la densidad de energía de tensión,

${\displaystyle T_{i}}$son los componentes de los vectores de tracción,

${\displaystyle u_{i}}$son los componentes de los vectores de desplazamiento,

${\displaystyle ds}$es una longitud incremental a lo largo de la ruta , y ${\displaystyle \Gamma }$

${\displaystyle \sigma _{ij}}$y son los tensores de tensión y deformación. ${\displaystyle \varepsilon _{ij}}$

Desde que los ingenieros se acostumbraron a utilizar K _Ic para caracterizar la tenacidad a la fractura, se ha utilizado una relación para reducir J _Ic a ella:

${\displaystyle K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,}$donde para tensión plana y para deformación plana. ${\displaystyle E^{*}=E}$ ${\displaystyle E^{*}={\frac {E}{1-\nu ^{2}}}}$

Modelo de zona cohesiva

Cuando una región significativa alrededor de la punta de una grieta ha sufrido una deformación plástica, se pueden utilizar otros métodos para determinar la posibilidad de una mayor extensión de la grieta y la dirección del crecimiento y ramificación de la grieta. Una técnica sencilla que se incorpora fácilmente a los cálculos numéricos es el método del modelo de zona cohesiva , que se basa en conceptos propuestos independientemente por Barenblatt ^[14] y Dugdale ^[15] a principios de los años 1960. La relación entre los modelos de Dugdale-Barenblatt y la teoría de Griffith fue discutida por primera vez por Willis en 1967. ^[16] La equivalencia de los dos métodos en el contexto de la fractura frágil fue demostrada por Rice en 1968. ^[13]

Tamaño del defecto de transición

Tensión de rotura en función del tamaño de la grieta

Sea un material con una resistencia a la fluencia y una tenacidad a la fractura en modo I . Según la mecánica de fracturas, el material fallará bajo tensión . Según la plasticidad, el material cederá cuando . Estas curvas se cruzan cuando . Este valor de se denomina tamaño de defecto de transición ., y depende de las propiedades del material de la estructura. Cuando , el fallo está regido por la fluencia plástica, y cuando el fallo está regido por la mecánica de fracturas. El valor de para aleaciones de ingeniería es de 100 mm y para cerámicas es de 0,001 mm. ^{[ cita requerida ]} Si suponemos que los procesos de fabricación pueden dar lugar a defectos del orden de micrómetros , entonces, se puede ver que las cerámicas tienen más probabilidades de fallar por fractura, mientras que las aleaciones de ingeniería fallarían por deformación plástica. ${\displaystyle \sigma _{Y}}$ ${\displaystyle K_{Ic}}$ ${\displaystyle \sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}}$ ${\displaystyle \sigma _{fail}=\sigma _{Y}}$ ${\displaystyle a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}}$ ${\displaystyle a}$ ${\displaystyle a_{t}}$ ${\displaystyle a<a_{t}}$ ${\displaystyle a>a_{t}}$ ${\displaystyle a_{t}}$

Análisis de fracturas de hormigón

El análisis de fracturas de hormigón es parte de la mecánica de fracturas que estudia la propagación de grietas y los modos de falla relacionados en el hormigón . ^[17] Como se usa ampliamente en la construcción, el análisis de fracturas y los modos de refuerzo son una parte importante del estudio del hormigón, y los diferentes hormigones se caracterizan en parte por sus propiedades de fractura. ^[18] Las fracturas comunes incluyen las fracturas en forma de cono que se forman alrededor de los anclajes bajo resistencia a la tracción.

Bažant (1983) propuso un modelo de banda de grietas para materiales como el hormigón cuya naturaleza homogénea cambia aleatoriamente en un cierto rango. ^[17] También observó que en el hormigón simple, el efecto del tamaño tiene una fuerte influencia en el factor de intensidad de tensión crítica , ^[19] y propuso la relación

${\displaystyle \sigma }$= / √(1+{ / }), ^{[19] [20]} ${\displaystyle \tau }$ ${\displaystyle d}$ ${\displaystyle \lambda }$ ${\displaystyle \delta }$

donde = factor de intensidad de tensión, = resistencia a la tracción, = tamaño de la muestra, = tamaño máximo del agregado, y = una constante empírica. ${\displaystyle \sigma }$ ${\displaystyle \tau }$ ${\displaystyle d}$ ${\displaystyle \delta }$ ${\displaystyle \lambda }$

Mecánica de fracturas atomísticas

La mecánica de fracturas atomísticas (AFM) es un campo relativamente nuevo que estudia el comportamiento y las propiedades de los materiales a escala atómica cuando se someten a fracturas. Integra conceptos de la mecánica de fracturas con simulaciones atomísticas para comprender cómo se inician las grietas, se propagan e interactúan con la microestructura de los materiales. Mediante el uso de técnicas como las simulaciones de dinámica molecular (MD), la AFM puede proporcionar información sobre los mecanismos fundamentales de la formación y el crecimiento de grietas, el papel de los enlaces atómicos y la influencia de los defectos y las impurezas del material en el comportamiento de las fracturas. ^[21]

Véase también

• AFGROW – Software de análisis de mecánica de fracturas y crecimiento de grietas por fatiga
• Falla del cono de hormigón  – Modo de falla de los anclajes en hormigón sometidos a fuerzas de tracción
• Degradación del hormigón  : Daño al hormigón que afecta a su resistencia mecánica y a su durabilidad.
• Terremoto  – Movimiento repentino de la corteza terrestre
• Fatiga  : inicio y propagación de grietas en un material debido a cargas cíclicas
• Falla (geología)  : Fractura o discontinuidad en la roca desplazada
• Teoría de fallas de materiales  : ciencia que predice si, cuándo y cómo un material determinado fallará bajo carga.
• Muesca (ingeniería)  : indentación producida externamente en un material plano
• Peridinámica , una formulación de la mecánica del medio continuo que está orientada a las deformaciones con discontinuidades, especialmente fracturas.
• Choque (mecánica)  : aceleración transitoria repentina
• Resistencia de materiales  – Comportamiento de objetos sólidos sometidos a tensiones y deformaciones
• Agrietamiento por corrosión bajo tensión  : crecimiento de grietas en un entorno corrosivo
• Mecánica de fracturas estructurales  – Campo de la ingeniería estructural

Referencias

1. TL Anderson (1995). Mecánica de fracturas: fundamentos y aplicaciones . CRC Press. ISBN 978-0849316562.
2. HL Ewalds; RJH Wanhill (1984). Mecánica de fracturas . Edward Arnold y Delftse Uitgevers Maatschappij. ISBN 978-0-7131-3515-2.
3. McMeeking, Robert M. (mayo de 2004). "La tasa de liberación de energía de una grieta de Griffith en un material piezoeléctrico". Mecánica de fracturas en ingeniería . 71 (7–8): 1149–1163. doi :10.1016/S0013-7944(03)00135-8. Archivado desde el original el 13 de febrero de 2022 . Consultado el 18 de diciembre de 2021 .
4. Lenci, Stefano (2001). "Análisis de una grieta en una interfaz débil". Revista Internacional de Fractura . 108 (3): 275–290. doi :10.1023/A:1011041409243. S2CID  115306909. Archivado desde el original el 2023-04-17 . Consultado el 2021-12-18 .
5. Griffith, AA (1921), "Los fenómenos de ruptura y flujo en sólidos", Philosophical Transactions of the Royal Society of London , 221 (582–593): 163–198, Bibcode :1921RSPTA.221..163G, doi : 10.1098/rsta.1921.0006.
6. E. Erdogan (2000) Mecánica de fracturas , Revista internacional de sólidos y estructuras, 37, págs. 171-183.
7. Irwin G (1957), Análisis de tensiones y deformaciones cerca del final de una grieta que atraviesa una placa , Journal of Applied Mechanics 24, 361–364.
8. Orowan, E., 1949. Fractura y resistencia de sólidos . Informes sobre el progreso en física XII, 185–232.
9. Liu, M.; et al. (2015). "Una solución semianalítica mejorada para el estrés en muescas de punta redonda" (PDF) . Ingeniería mecánica de fracturas . 149 : 134–143. doi :10.1016/j.engfracmech.2015.10.004. S2CID  51902898. Archivado (PDF) desde el original el 2018-07-13 . Consultado el 2017-11-01 .
10. Weisshaar, Terry (28 de julio de 2011). Estructuras aeroespaciales: una introducción a los problemas fundamentales . West Lafayette, IN: Universidad de Purdue.
11. "Tamaño de la zona plástica de la punta de la grieta". Manual para el diseño tolerante a daños . LexTech, Inc. Archivado desde el original el 21 de noviembre de 2016. Consultado el 20 de noviembre de 2016 .
12. "Retardo". Manual de diseño tolerante a daños . LexTech, Inc. Archivado desde el original el 21 de noviembre de 2016. Consultado el 20 de noviembre de 2016 .
13. Rice, JR (1968), "Una integral independiente de la trayectoria y el análisis aproximado de la concentración de la deformación por entallas y grietas" (PDF) , Journal of Applied Mechanics , 35 (2): 379–386, Bibcode :1968JAM....35..379R, CiteSeerX 10.1.1.1023.7604 , doi :10.1115/1.3601206, archivado (PDF) desde el original el 28-08-2008 , recuperado 31-05-2008 .
14. Barenblatt, GI (1962), "La teoría matemática de las grietas de equilibrio en fractura frágil" (PDF) , Advances in Applied Mechanics , 7 : 55–129, doi :10.1016/s0065-2156(08)70121-2, ISBN 9780120020072, archivado (PDF) del original el 17 de abril de 2023 , consultado el 8 de junio de 2022
15. Dugdale, DS (1960), "Fluidez de láminas de acero que contienen ranuras", Journal of the Mechanics and Physics of Solids , 8 (2): 100–104, Bibcode :1960JMPSo...8..100D, doi :10.1016/0022-5096(60)90013-2, S2CID  136484892
16. Willis, JR (1967), "Una comparación de los criterios de fractura de Griffith y Barenblatt", Journal of the Mechanics and Physics of Solids , 15 (3): 151–162, Bibcode :1967JMPSo..15..151W, doi :10.1016/0022-5096(67)90029-4.
17. "Mecánica de fracturas para hormigón estructural" (PDF) . Consultado el 13 de abril de 2013 .
18. Notas de la clase sobre mecánica de fracturas, por Victor E. Saouma
19. Bažant, ZP y Planas, J. (1998). Efecto de la fractura y el tamaño en el hormigón y otros materiales cuasi frágiles . CRC Press, Boca Raton, Florida
20. Bažant, ZP y Pang, S.-D. (2006) “Estadísticas basadas en la mecánica del riesgo de falla de estructuras cuasi frágiles y efecto del tamaño en los factores de seguridad”. Proc. Nat'l Acad. Sci., EE. UU. 103 (25), págs. 9434–9439
21. Modelado atomístico de fallas de materiales. doi :10.1007/978-0-387-76426-9.

Lectura adicional

• Buckley, CP "Falla de materiales", Notas de clase (2005), Universidad de Oxford .
• Davidge, RW, Comportamiento mecánico de la cerámica , Cambridge Solid State Science Series, (1979)
• Demaid, Adrian, Fail Safe , Universidad Abierta (2004)
• Green, D., Introducción a las propiedades mecánicas de la cerámica , Cambridge Solid State Science Series, Eds. Clarke, DR, Suresh, S., Ward, IM (1998)
• Tipper, Constance Fligg (1962). La historia de la fractura frágil. Cambridge UP
• Lawn, BR, Fractura de sólidos frágiles , Cambridge Solid State Science Series, 2.ª edición (1993)
• Farahmand, B., Bockrath, G. y Glassco, J. (1997) Mecánica de fatiga y fractura de piezas de alto riesgo, Chapman & Hall. ISBN 978-0-412-12991-9 . 
• Chen, X., Mai, Y.-W., Mecánica de fracturas de materiales electromagnéticos: teoría de campos no lineales y aplicaciones , Imperial College Press, (2012)
• AN Gent, WV Mars, En: James E. Mark, Burak Erman y Mike Roland, Editor(es), Capítulo 10 – Resistencia de los elastómeros, La ciencia y la tecnología del caucho , Cuarta edición, Academic Press, Boston, 2013, págs. 473–516, ISBN 9780123945846 , 10.1016/B978-0-12-394584-6.00010-8 
• Zehnder, Alan. Mecánica de fracturas , SpringerLink, (2012).

Enlaces externos

• Notas sobre mecánica de fracturas no lineales del profesor John Hutchinson, Universidad de Harvard
• Notas sobre fractura de películas delgadas y multicapas por el profesor John Hutchinson, Universidad de Harvard
• Mecánica de fracturas por Piet Schreurs, TU Eindhoven, Países Bajos