conjunto convexo

En geometría, conjunto cuya intersección con cada recta es un solo segmento de recta.

Ilustración de un conjunto convexo con forma de círculo deformado. El segmento de línea que une los puntos xey se encuentra completamente dentro del conjunto, ilustrado en verde. Como esto es cierto para cualquier ubicación potencial de dos puntos dentro del conjunto, el conjunto es convexo.

Ilustración de un conjunto no convexo. El segmento de línea que une los puntos x e y se extiende parcialmente fuera del conjunto, ilustrado en rojo, y la intersección del conjunto con la línea ocurre en dos lugares, ilustrado en negro.

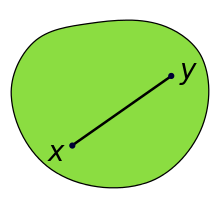
En geometría , un subconjunto de un espacio euclidiano , o más generalmente un espacio afín sobre los reales , es convexo si, dados dos puntos cualesquiera del subconjunto, el subconjunto contiene todo el segmento de recta que los une. De manera equivalente, un conjunto convexo o una región convexa es un subconjunto que intersecta cada línea en un solo segmento de línea (posiblemente vacío). ^{[1] [2] Por ejemplo, un} cubo sólido es un conjunto convexo, pero cualquier cosa que sea hueca o tenga una sangría, por ejemplo, una forma de media luna , no es convexa.

El límite de un conjunto convexo en el plano es siempre una curva convexa . La intersección de todos los conjuntos convexos que contienen un subconjunto dado A del espacio euclidiano se llama casco convexo de A. Es el conjunto convexo más pequeño que contiene A.

Una función convexa es una función de valor real definida en un intervalo con la propiedad de que su epígrafe (el conjunto de puntos sobre o encima de la gráfica de la función) es un conjunto convexo. La minimización convexa es un subcampo de optimización que estudia el problema de minimizar funciones convexas sobre conjuntos convexos. La rama de las matemáticas dedicada al estudio de las propiedades de conjuntos convexos y funciones convexas se denomina análisis convexo .

La noción de conjunto convexo se puede generalizar como se describe a continuación.

Definiciones

Una función es convexa si y sólo si su epígrafe , la región (en verde) encima de su gráfica (en azul), es un conjunto convexo.

Sea S un espacio vectorial o un espacio afín sobre los números reales o, más generalmente, sobre algún campo ordenado (esto incluye los espacios euclidianos, que son espacios afines). Un subconjunto C de S es convexo si , para todo x e y en C , el segmento de línea que conecta x e y está incluido en C.

Esto significa que la combinación afín (1 − t ) x + ty pertenece a C para todo x,y en C y t en el intervalo [0, 1] . Esto implica que la convexidad es invariante bajo transformaciones afines . Además, implica que un conjunto convexo en un espacio vectorial topológico real o complejo está conexo por caminos (y por lo tanto también conexo ).

Un conjunto C esestrictamente convexo si cada puntoen el segmento de línea que conectaxeydistintosde los puntos finales está dentro delinteriortopológicodeC. Un subconjunto convexo cerrado es estrictamente convexo si y sólo si cada uno de suspuntos límitees unpunto extremo. ^[3]

Un conjunto C es absolutamente convexo si es convexo y equilibrado .

Ejemplos

Los subconjuntos convexos de R (el conjunto de los números reales) son los intervalos y los puntos de R. Algunos ejemplos de subconjuntos convexos del plano euclidiano son los polígonos regulares sólidos , los triángulos sólidos y las intersecciones de triángulos sólidos. Algunos ejemplos de subconjuntos convexos de un espacio tridimensional euclidiano son los sólidos de Arquímedes y los sólidos platónicos . Los poliedros de Kepler-Poinsot son ejemplos de conjuntos no convexos.

Conjunto no convexo

Un conjunto que no es convexo se llama conjunto no convexo . Un polígono que no es un polígono convexo a veces se llama polígono cóncavo , ^[4] y algunas fuentes usan de manera más general el término conjunto cóncavo para referirse a un conjunto no convexo, ^[5] pero la mayoría de las autoridades prohíben este uso. ^{[6] [7]}

El complemento de un conjunto convexo, como el epígrafe de una función cóncava , a veces se denomina conjunto convexo inverso , especialmente en el contexto de la optimización matemática . ^[8]

Propiedades

Dados r puntos u ₁ , ..., u _r en un conjunto convexo S , y r números no negativos λ ₁ , ..., λ _r tales que λ ₁ + ... + λ _r = 1 , la combinación afín

$${\displaystyle \sum _{k=1}^{r}\lambda _{k}u_{k}}$$

S. r = 2

Tal combinación afín se llama combinación convexa de u ₁ , ..., u _r .

Intersecciones y uniones

La colección de subconjuntos convexos de un espacio vectorial, un espacio afín o un espacio euclidiano tiene las siguientes propiedades: ^{[9] [10]}

1. El conjunto vacío y todo el espacio son convexos.
2. La intersección de cualquier colección de conjuntos convexos es convexa.
3. La unión de una secuencia de conjuntos convexos es convexa, si forman una cadena no decreciente para su inclusión. Para esta propiedad, la restricción a cadenas es importante, ya que la unión de dos conjuntos convexos no tiene por qué ser convexa.

Conjuntos convexos cerrados

Los conjuntos convexos cerrados son conjuntos convexos que contienen todos sus puntos límite . Se pueden caracterizar como intersecciones de semiespacios cerrados (conjuntos de puntos en el espacio que se encuentran sobre y a un lado de un hiperplano ).

De lo que se acaba de decir, queda claro que tales intersecciones son convexas y también serán conjuntos cerrados. Para demostrar lo contrario, es decir, todo conjunto convexo cerrado puede representarse como tal intersección, se necesita el teorema del hiperplano de soporte en la forma de que para un conjunto convexo cerrado C dado y un punto P fuera de él, hay un semiespacio cerrado H que contiene C y no P . El teorema del hiperplano de apoyo es un caso especial del teorema de análisis funcional de Hahn-Banach .

Conjuntos convexos y rectángulos.

Sea C un cuerpo convexo en el plano (un conjunto convexo cuyo interior no está vacío). Podemos inscribir un rectángulo r en C tal que una copia homotética R de r esté circunscrita alrededor de C. La relación de homotecia positiva es como máximo 2 y: ^[11]

$${\displaystyle {\tfrac {1}{2}}\cdot \operatorname {Area} (R)\leq \operatorname {Area} (C)\leq 2\cdot \operatorname {Area} (r)}$$

Diagramas de Blaschke-Santaló

El conjunto de todos los cuerpos convexos planos se puede parametrizar en términos del diámetro del cuerpo convexo D , su radio interior r (el círculo más grande contenido en el cuerpo convexo) y su circunradio R (el círculo más pequeño que contiene el cuerpo convexo). De hecho, este conjunto puede describirse mediante el conjunto de desigualdades dado por ^{[12] [13]} ${\displaystyle {\mathcal {K}}^{2}}$

$${\displaystyle 2r\leq D\leq 2R}$$

$${\displaystyle R\leq {\frac {\sqrt {3}}{3}}D}$$

$${\displaystyle r+R\leq D}$$

$${\displaystyle D^{2}{\sqrt {4R^{2}-D^{2}}}\leq 2R(2R+{\sqrt {4R^{2}-D^{2}}})}$$

gR ²rRD​​RrDR^[13]

Diagrama de Blaschke-Santaló ( r , D , R ) para cuerpos planos convexos. denota el segmento de línea, el triángulo equilátero, el triángulo de Reuleaux y el círculo unitario. ${\displaystyle \mathbb {L} }$ ${\displaystyle \mathbb {I} _{\frac {\pi }{3}}}$ ${\displaystyle \mathbb {RT} }$ ${\displaystyle \mathbb {B} _{2}}$

Alternativamente, el conjunto también se puede parametrizar por su ancho (la distancia más pequeña entre dos hiperplanos de soporte paralelos diferentes), perímetro y área. ^{[12] [13]} ${\displaystyle {\mathcal {K}}^{2}}$

Otras propiedades

Sea X un espacio vectorial topológico y convexo. ${\displaystyle C\subseteq X}$

• ${\displaystyle \operatorname {Cl} C}$y ambos son convexos (es decir, el cierre y el interior de conjuntos convexos son convexos). ${\displaystyle \operatorname {Int} C}$
• Si y entonces (dónde ). ${\displaystyle a\in \operatorname {Int} C}$ ${\displaystyle b\in \operatorname {Cl} C}$ ${\displaystyle [a,b[\,\subseteq \operatorname {Int} C}$ ${\displaystyle [a,b[\,:=\left\{(1-r)a+rb:0\leq r<1\right\}}$
• Si entonces: ${\displaystyle \operatorname {Int} C\neq \emptyset }$
  • ${\displaystyle \operatorname {cl} \left(\operatorname {Int} C\right)=\operatorname {Cl} C}$, y
  • ${\displaystyle \operatorname {Int} C=\operatorname {Int} \left(\operatorname {Cl} C\right)=C^{i}}$, donde está el interior algebraico de C . ${\displaystyle C^{i}}$

Cascos convexos y sumas de Minkowski

Cascos convexos

Cada subconjunto A del espacio vectorial está contenido dentro de un conjunto convexo más pequeño (llamado casco convexo de A ), es decir, la intersección de todos los conjuntos convexos que contienen A. El operador de casco convexo Conv() tiene las propiedades características de un operador de casco :

• extenso : S  ⊆ Conv( S ) ,
• no decreciente : S  ⊆  T implica que Conv( S ) ⊆ Conv( T ) , y
• idempotente : Conv(Conv( S )) = Conv( S ) .

La operación de casco convexo es necesaria para que el conjunto de conjuntos convexos forme una red , en la que la operación " unir " es el casco convexo de la unión de dos conjuntos convexos.

$${\displaystyle \operatorname {Conv} (S)\vee \operatorname {Conv} (T)=\operatorname {Conv} (S\cup T)=\operatorname {Conv} {\bigl (}\operatorname {Conv} (S)\cup \operatorname {Conv} (T){\bigr )}.}$$

red

Adición de Minkowski

Suma de conjuntos de Minkowski . La suma de los cuadrados Q ₁ =[0,1] ² y Q ₂ =[1,2] ² es el cuadrado Q ₁ +Q ₂ =[1,3] ² .

En un espacio vectorial real, la suma de Minkowski de dos conjuntos (no vacíos), S ₁ y S ₂ , se define como el conjunto S ₁  +  S ₂ formado por la suma de vectores por elementos de los conjuntos de sumandos.

$${\displaystyle S_{1}+S_{2}=\{x_{1}+x_{2}:x_{1}\in S_{1},x_{2}\in S_{2}\}.}$$

suma de MinkowskiS _n

$${\displaystyle \sum _{n}S_{n}=\left\{\sum _{n}x_{n}:x_{n}\in S_{n}\right\}.}$$

Para la suma de Minkowski, el conjunto cero  {0} que contiene solo el vector cero  0 tiene especial importancia : para cada subconjunto S no vacío de un espacio vectorial

$${\displaystyle S+\{0\}=S;}$$

{0}elemento identidad^[14]

Cascos convexos de sumas de Minkowski

La suma de Minkowski se comporta bien con respecto a la operación de tomar cascos convexos, como lo muestra la siguiente proposición:

Sean S ₁ , S ₂ subconjuntos de un espacio vectorial real, la cáscara convexa de su suma de Minkowski es la suma de Minkowski de sus cáscaras convexas

$${\displaystyle \operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).}$$

Este resultado es válido de manera más general para cada colección finita de conjuntos no vacíos:

$${\displaystyle {\text{Conv}}\left(\sum _{n}S_{n}\right)=\sum _{n}{\text{Conv}}\left(S_{n}\right).}$$

En terminología matemática, las operaciones de suma de Minkowski y de formación de cascos convexos son operaciones de conmutación . ^{[15] [16]}

Sumas de Minkowski de conjuntos convexos

La suma de Minkowski de dos conjuntos convexos compactos es compacta. La suma de un conjunto convexo compacto y un conjunto convexo cerrado es cerrada. ^[17]

El siguiente famoso teorema, demostrado por Dieudonné en 1966, da una condición suficiente para que la diferencia de dos subconjuntos convexos cerrados sea cerrada. ^[18] Utiliza el concepto de cono de recesión de un subconjunto convexo no vacío S , definido como:

$${\displaystyle \operatorname {rec} S=\left\{x\in X\,:\,x+S\subseteq S\right\},}$$

cono convexoS ${\displaystyle 0\in X}$ ${\displaystyle S+\operatorname {rec} S=S}$ ${\displaystyle \operatorname {rec} S}$ ${\displaystyle s_{0}\in S}$

$${\displaystyle \operatorname {rec} S=\bigcap _{t>0}t(S-s_{0}).}$$

Teorema (Dieudonné). Sean A y B subconjuntos no vacíos, cerrados y convexos de un espacio vectorial topológico localmente convexo tal que sea un subespacio lineal. Si A o B son localmente compactos, entonces A  −  B es cerrado. ${\displaystyle \operatorname {rec} A\cap \operatorname {rec} B}$

Generalizaciones y extensiones de la convexidad.

La noción de convexidad en el espacio euclidiano puede generalizarse modificando la definición en unos u otros aspectos. Se utiliza el nombre común de "convexidad generalizada" porque los objetos resultantes conservan ciertas propiedades de los conjuntos convexos.

Conjuntos estrella-convexos (en forma de estrella)

Sea C un conjunto en un espacio vectorial real o complejo. C es estrella convexa ( en forma de estrella) si existe un x ₀ en C tal que el segmento de línea desde x ₀ hasta cualquier punto y en C esté contenido en C. Por lo tanto, un conjunto convexo no vacío siempre es convexo en estrella, pero un conjunto convexo en estrella no siempre es convexo.

Convexidad ortogonal

Un ejemplo de convexidad generalizada es la convexidad ortogonal . ^[19]

Un conjunto S en el espacio euclidiano se llama ortogonalmente convexo u ortoconvexo , si cualquier segmento paralelo a cualquiera de los ejes de coordenadas que conectan dos puntos de S se encuentra totalmente dentro de S. Es fácil demostrar que una intersección de cualquier colección de conjuntos ortoconvexos es ortoconvexa. Algunas otras propiedades de los conjuntos convexos también son válidas.

Geometría no euclidiana

La definición de conjunto convexo y casco convexo se extiende naturalmente a geometrías que no son euclidianas al definir un conjunto geodésicamente convexo como aquel que contiene las geodésicas que unen dos puntos cualesquiera del conjunto.

Topología de orden

La convexidad se puede extender para un conjunto X totalmente ordenado dotado de la topología de orden . ^[20]

Sea Y ⊆ X . El subespacio Y es un conjunto convexo si para cada par de puntos a , b en Y tal que a ≤ b , el intervalo [ a , b ] = { x ∈ X | a ≤ x ≤ b } está contenido en Y . Es decir, Y es convexo si y sólo si para todo a , b en Y , a ≤ b implica [ a , b ] ⊆ Y.

Un conjunto convexo no es conexo en general: un contraejemplo lo da el subespacio {1,2,3} en Z , que es a la vez convexo y no conexo.

Espacios de convexidad

La noción de convexidad puede generalizarse a otros objetos, si ciertas propiedades de la convexidad se seleccionan como axiomas .

Dado un conjunto X , una convexidad sobre X es una colección 𝒞 de subconjuntos de X que satisfacen los siguientes axiomas: ^{[9] [10] [21]}

1. El conjunto vacío y X están en 𝒞
2. La intersección de cualquier conjunto de 𝒞 está en 𝒞 .
3. La unión de una cadena (con respecto a la relación de inclusión ) de elementos de 𝒞 está en 𝒞 .

Los elementos de 𝒞 se llaman conjuntos convexos y el par ( X , 𝒞 ) se llama espacio de convexidad . Para la convexidad ordinaria, los dos primeros axiomas se cumplen y el tercero es trivial.

Para obtener una definición alternativa de convexidad abstracta, más adecuada para la geometría discreta , consulte las geometrías convexas asociadas con los antimatroides .

espacios convexos

La convexidad se puede generalizar como una estructura algebraica abstracta: un espacio es convexo si es posible tomar combinaciones convexas de puntos.

Ver también

• Conjunto absorbente
• Problemas algorítmicos en conjuntos convexos.
• Conjunto acotado (espacio vectorial topológico)
• Teorema del punto fijo de Brouwer
• Convexidad compleja
• casco convexo
• Serie convexa
• Espacio métrico convexo
• Teorema de Carathéodory (casco convexo)
• Teoría de Choquet
• teorema de helly
• Casco holomorfamente convexo
• Conjunto integralmente convexo
• elipsoide de juan
• Pseudoconvexidad
• teorema del radón
• Lema de Shapley-Folkman
• conjunto simétrico

Referencias

1. Morris, Carla C.; Stark, Robert M. (24 de agosto de 2015). Matemáticas finitas: modelos y aplicaciones. John Wiley e hijos. pag. 121.ISBN _ 9781119015383. Consultado el 5 de abril de 2017 .
2. Kjeldsen, Tinne Hoff. "Historia de la convexidad y la programación matemática" (PDF) . Actas del Congreso Internacional de Matemáticos (ICM 2010): 3233–3257. doi :10.1142/9789814324359_0187. Archivado desde el original (PDF) el 11 de agosto de 2017 . Consultado el 5 de abril de 2017 .
3. Halmos, Paul R. (8 de noviembre de 1982). Un libro de problemas espaciales de Hilbert . Textos de Posgrado en Matemáticas . vol. 19 (2ª ed.). Nueva York: Springer-Verlag . pag. 5.ISBN _ 978-0-387-90685-0. OCLC  8169781.
4. McConnell, Jeffrey J. (2006). Gráficos por computadora: la teoría a la práctica. pag. 130.ISBN _ 0-7637-2250-2..
5. Weisstein, Eric W. "Cóncavo". MundoMatemático .
6. Takayama, Akira (1994). Métodos analíticos en economía. Prensa de la Universidad de Michigan. pag. 54.ISBN _ 9780472081356. Una confusión que se ve a menudo es la de un "conjunto cóncavo". Las funciones cóncavas y convexas designan ciertas clases de funciones, no de conjuntos, mientras que un conjunto convexo designa una cierta clase de conjuntos, y no una clase de funciones. Un "conjunto cóncavo" confunde conjuntos con funciones.
7. Corbae, decano; Stinchcombe, Maxwell B.; Zeman, Juraj (2009). Introducción al análisis matemático para la teoría económica y la econometría. Prensa de la Universidad de Princeton. pag. 347.ISBN _ 9781400833085. No existe un conjunto cóncavo.
8. Meyer, Robert (1970). "La validez de una familia de métodos de optimización" (PDF) . Revista SIAM de Control y Optimización . 8 : 41–54. doi :10.1137/0308003. SEÑOR  0312915..
9. Soltan, Valeriu, Introducción a la teoría axiomática de la convexidad , Ştiinţa, Chişinău , 1984 (en ruso).
10. Cantante, Ivan (1997). Análisis convexo abstracto . Serie de monografías y textos avanzados de la Sociedad Canadiense de Matemáticas. Nueva York: John Wiley & Sons, Inc. págs. xxii+491. ISBN 0-471-16015-6. SEÑOR  1461544.
11. Lassak, M. (1993). "Aproximación de cuerpos convexos mediante rectángulos". Geometriae Dedicata . 47 : 111-117. doi :10.1007/BF01263495. S2CID  119508642.
12. Santaló, L. (1961). "Sobre los sistemas completos de desigualdades entre tres elementos de una figura convexa plana". Matemáticas Notae . 17 : 82-104.
13. Brandenberg, René; González Merino, Bernardo (2017). "Un diagrama tridimensional completo de Blaschke-Santaló". Desigualdades y aplicaciones matemáticas (2): 301–348. arXiv : 1404.6808 . doi : 10.7153/mia-20-22 . ISSN  1331-4343.
14. El conjunto vacío es importante en la suma de Minkowski, porque el conjunto vacío aniquila todos los demás subconjuntos: para cada subconjunto S de un espacio vectorial, su suma con el conjunto vacío es vacía :. ${\displaystyle S+\emptyset =\emptyset }$
15. Teorema 3 (páginas 562–563): Krein, M .; Šmulian, V. (1940). "En conjuntos regularmente convexos en el espacio conjugado con un espacio de Banach". Anales de Matemáticas . Segunda Serie. 41 (3): 556–583. doi :10.2307/1968735. JSTOR  1968735.
16. Para conocer la conmutatividad de la suma y convexificación de Minkowski , consulte el Teorema 1.1.2 (páginas 2-3) en Schneider; esta referencia analiza gran parte de la literatura sobre los cascos convexos de las sumas de Minkowski en su "Capítulo 3 Adición de Minkowski" (páginas 126-196): Schneider, Rolf (1993). Cuerpos convexos: la teoría de Brunn-Minkowski. Enciclopedia de matemáticas y sus aplicaciones. vol. 44. Cambridge: Prensa de la Universidad de Cambridge. págs. xiv+490. ISBN  0-521-35220-7. SEÑOR  1216521.
17. Lema 5.3: Aliprantis, CD; Frontera, KC (2006). Análisis dimensional infinito, una guía para el autoestopista . Berlín: Springer. ISBN 978-3-540-29587-7.
18. Zălinescu, C. (2002). Análisis convexo en espacios vectoriales generales . River Edge, Nueva Jersey: World Scientific Publishing Co., Inc. p. 7.ISBN _ 981-238-067-1. SEÑOR  1921556.
19. Rawlins GJE y Wood D, "Ortoconvexidad y sus generalizaciones", en: Morfología computacional , 137-152. Elsevier , 1988.
20. Munkres, James ; Topología , Prentice Hall; 2ª edición (28 de diciembre de 1999). ISBN 0-13-181629-2 . 
21. van De Vel, Marcel LJ (1993). Teoría de estructuras convexas . Biblioteca de Matemáticas de Holanda Septentrional. Ámsterdam: North-Holland Publishing Co. págs. xvi+540. ISBN 0-444-81505-8. SEÑOR  1234493.

enlaces externos

• "Subconjunto convexo". Enciclopedia de Matemáticas . Prensa EMS . 2001 [1994].
• Conferencias sobre conjuntos convexos, notas de Niels Lauritzen, en la Universidad de Aarhus , marzo de 2010.