Klaus Friedrich Roth FRS (29 de octubre de 1925 - 10 de noviembre de 2015) fue un matemático británico nacido en Alemania que ganó la Medalla Fields por demostrar el teorema de Roth sobre la aproximación diofántica de números algebraicos . También fue ganador de la Medalla De Morgan y la Medalla Sylvester , y miembro de la Royal Society .
Roth se mudó a Inglaterra cuando era niño en 1933 para escapar de los nazis y se educó en la Universidad de Cambridge y en el University College London , terminando su doctorado en 1950. Enseñó en el University College London hasta 1966, cuando ocupó una cátedra en el Imperial College. Londres . Se jubiló en 1988.
Más allá de su trabajo sobre la aproximación diofántica, Roth hizo importantes contribuciones a la teoría de conjuntos libres de progresión en combinatoria aritmética y a la teoría de las irregularidades de la distribución . También fue conocido por sus investigaciones sobre sumas de potencias , sobre el gran tamiz , sobre el problema del triángulo de Heilbronn y sobre el empaquetado de cuadrados en un cuadrado . Fue coautor del libro Secuencias sobre secuencias enteras .
Roth nació en una familia judía en Breslau , Prusia , el 29 de octubre de 1925. Sus padres se establecieron con él en Londres para escapar de la persecución nazi en 1933, y se crió y educó en el Reino Unido. [1] [2] Su padre, un abogado, había estado expuesto a gas venenoso durante la Primera Guerra Mundial y murió cuando Roth aún era joven. Roth se convirtió en alumno de la St Paul's School de Londres de 1939 a 1943, y con el resto de la escuela fue evacuado de Londres a Easthampstead Park durante el Blitz . En la escuela, era conocido por su habilidad tanto en ajedrez como en matemáticas. Intentó unirse al Cuerpo de Entrenamiento Aéreo , pero fue bloqueado durante algunos años por ser alemán y luego por carecer de la coordinación necesaria para ser piloto. [2]
Roth leyó matemáticas en Peterhouse, Cambridge , y jugó el primer tablero para el equipo de ajedrez de Cambridge, [2] terminando en 1945. [3] A pesar de su habilidad en matemáticas, sólo logró honores de tercera clase en los Tripos Matemáticos , debido a su pobre capacidad para tomar exámenes. Su tutor de Cambridge, John Charles Burkill , no apoyó que Roth continuara en matemáticas y le recomendó que aceptara "algún trabajo comercial con un sesgo estadístico". [2] En cambio, se convirtió brevemente en maestro de escuela en Gordonstoun , entre terminar en Cambridge y comenzar sus estudios de posgrado. [1] [2]
Por recomendación de Harold Davenport , fue aceptado en 1946 en un programa de maestría en matemáticas en el University College de Londres , donde trabajó bajo la supervisión de Theodor Estermann . [2] Completó una maestría allí en 1948 y un doctorado en 1950. [3] Su tesis fue Prueba de que casi todos los números enteros positivos son sumas de un cuadrado, un cubo positivo y una cuarta potencia . [4]
Al recibir su maestría en 1948, Roth se convirtió en profesor asistente en el University College de Londres y en 1950 fue ascendido a profesor. [5] Sus contribuciones más significativas, sobre la aproximación diofántica, las secuencias libres de progresión y la discrepancia, se publicaron a mediados de la década de 1950, y en 1958 recibió la Medalla Fields, el mayor honor de los matemáticos. [2] [6] Sin embargo, no fue hasta 1961 que fue ascendido a profesor titular. [1] Durante este período, continuó trabajando en estrecha colaboración con Harold Davenport. [2]
Se tomó unos años sabáticos en el Instituto Tecnológico de Massachusetts a mediados de los años 1950 y mediados de los 1960, y consideró seriamente migrar a los Estados Unidos. Walter Hayman y Patrick Linstead contrarrestaron esta posibilidad, que vieron como una amenaza para las matemáticas británicas, con una oferta de una cátedra de matemáticas puras en el Imperial College de Londres , y Roth aceptó la cátedra en 1966. [2] Mantuvo este puesto hasta que se hizo oficial jubilación en 1988. [1] Permaneció en el Imperial College como profesor visitante hasta 1996. [3]
Las conferencias de Roth solían ser muy claras, pero en ocasiones podían resultar erráticas. [2] El Proyecto de Genealogía de Matemáticas lo enumera como si tuviera sólo dos estudiantes de doctorado, [4] pero uno de ellos, William Chen, quien continuó el trabajo de Roth en la teoría de la discrepancia, se convirtió en miembro de la Sociedad Australiana de Matemáticas y jefe del departamento de matemáticas en Universidad Macquarie . [7]
En 1955, Roth se casó con Mélèk Khaïry, quien había llamado su atención cuando ella era estudiante en su primera conferencia; Khaïry era hija del senador egipcio Khaïry Pacha [1] [2] Llegó a trabajar para el departamento de psicología del University College de Londres, donde publicó una investigación sobre los efectos de las toxinas en ratas. [8] Tras la jubilación de Roth, se trasladaron a Inverness ; Roth dedicó una sala de su casa al baile latino, un interés compartido por ellos. [2] [9] Khaïry murió en 2002 y Roth murió en Inverness el 10 de noviembre de 2015 a la edad de 90 años. [1] [2] [3] No tuvieron hijos y Roth dedicó la mayor parte de su patrimonio, más un millón de libras, a dos organizaciones de salud "para ayudar a las personas mayores y enfermas que viven en la ciudad de Inverness". Envió la Medalla Fields con un legado más pequeño a Peterhouse. [10]
Roth era conocido como un solucionador de problemas en matemáticas, más que como un constructor de teorías. Harold Davenport escribe que la "moraleja del trabajo del Dr. Roth" es que "los grandes problemas no resueltos de las matemáticas aún pueden ceder ante un ataque directo, por difíciles y prohibitivos que parezcan y por mucho esfuerzo que ya se haya invertido en ellos". [6] Sus intereses de investigación abarcaron varios temas en teoría de números , teoría de discrepancia y teoría de secuencias enteras .
La materia de aproximación diofántica busca aproximaciones precisas de números irracionales mediante números racionales . La cuestión de con qué precisión se podían aproximar los números algebraicos se conoció como el problema de Thue-Siegel, después de los avances previos en esta cuestión realizados por Axel Thue y Carl Ludwig Siegel . La precisión de la aproximación se puede medir mediante el exponente de aproximación de un número , definido como el número más grande que tiene infinitas aproximaciones racionales . Si el exponente de aproximación es grande, entonces tiene aproximaciones más precisas que un número cuyo exponente es menor. El exponente de aproximación más pequeño posible es dos: incluso los números más difíciles de aproximar se pueden aproximar con el exponente dos usando fracciones continuas . [3] [6] Antes del trabajo de Roth, se creía que los números algebraicos podían tener un exponente de aproximación mayor, relacionado con el grado del polinomio que definía el número. [2]
En 1955, Roth publicó lo que hoy se conoce como teorema de Roth , zanjando por completo esta cuestión. Su teorema falsificó la supuesta conexión entre el exponente de aproximación y el grado, y demostró que, en términos del exponente de aproximación, los números algebraicos son los números irracionales que se aproximan con menor precisión. Más precisamente, demostró que para los números algebraicos irracionales, el exponente de aproximación es siempre exactamente dos. [3] En un estudio del trabajo de Roth presentado por Harold Davenport en el Congreso Internacional de Matemáticos en 1958, cuando Roth recibió la Medalla Fields, Davenport llamó a este resultado el "mayor logro" de Roth. [6]
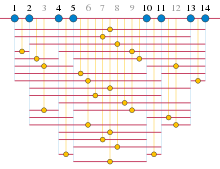
Otro resultado llamado " teorema de Roth ", de 1953, está en combinatoria aritmética y se refiere a secuencias de números enteros sin tres en progresión aritmética . Estas secuencias habían sido estudiadas en 1936 por Paul Erdős y Pál Turán , quienes conjeturaron que debían ser escasas. [11] [a] Sin embargo, en 1942, Raphaël Salem y Donald C. Spencer construyeron subconjuntos libres de progresión de números de a de tamaño proporcional a , para cada . [12]
Roth reivindicó a Erdős y Turán demostrando que no es posible que el tamaño de tal conjunto sea proporcional a : cada conjunto denso de números enteros contiene una progresión aritmética de tres términos. Su prueba utiliza técnicas de la teoría analítica de números , incluido el método del círculo de Hardy-Littlewood, para estimar el número de progresiones en una secuencia dada y mostrar que, cuando la secuencia es lo suficientemente densa, este número es distinto de cero. [2] [13]
Posteriormente, otros autores reforzaron la limitación de Roth sobre el tamaño de los conjuntos libres de progresión. [14] Un fortalecimiento en una dirección diferente, el teorema de Szemerédi , muestra que los conjuntos densos de números enteros contienen progresiones aritméticas arbitrariamente largas. [15]

Aunque el trabajo de Roth sobre la aproximación diofántica le valió el mayor reconocimiento, es su investigación sobre las irregularidades de la distribución de la que (según un obituario de William Chen y Bob Vaughan ) estaba más orgulloso. [2] Su artículo de 1954 sobre este tema sentó las bases de la teoría moderna de la discrepancia . Se trata de la ubicación de puntos en un cuadrado unitario de modo que, para cada rectángulo delimitado entre el origen y un punto del cuadrado, el área del rectángulo esté bien aproximada por el número de puntos que contiene. [2]
Roth midió esta aproximación mediante la diferencia al cuadrado entre el número de puntos y multiplicado por el área, y demostró que para un rectángulo elegido al azar el valor esperado de la diferencia al cuadrado es logarítmico en . Este resultado es el mejor posible y mejora significativamente un límite anterior sobre el mismo problema de Tatyana Pavlovna Ehrenfest . [16] A pesar del trabajo previo de Ehrenfest y Johannes van der Corput sobre el mismo problema, Roth era conocido por alardear de que este resultado "inició un tema". [2]
Algunos de los primeros trabajos de Roth incluyeron un artículo de 1949 sobre sumas de potencias , que muestra que casi todos los números enteros positivos pueden representarse como una suma de un cuadrado, un cubo y una cuarta potencia, y un artículo de 1951 sobre los espacios entre números libres de cuadrados , describe como "bastante sensacionalista" y "de considerable importancia", respectivamente, por Chen y Vaughan. [2] Su conferencia inaugural en el Imperial College se refirió al gran tamiz : delimitar el tamaño de conjuntos de números enteros a partir de los cuales se han prohibido muchas clases de congruencia de números módulo primos . [17] Roth había publicado previamente un artículo sobre este problema en 1965.

Otro de los intereses de Roth fue el problema del triángulo de Heilbronn , de colocar puntos en un cuadrado para evitar triángulos de área pequeña. Su artículo de 1951 sobre el problema fue el primero en demostrar un límite superior no trivial del área que se puede alcanzar. Finalmente publicó cuatro artículos sobre este problema, el último en 1976. [18] Roth también hizo avances significativos en el empaquetado de cuadrados en un cuadrado . Si los cuadrados unitarios se empaquetan en un cuadrado de la manera obvia, paralela al eje, entonces para valores de eso están justo por debajo de un número entero, casi el área puede dejarse sin cubrir. Después de que Paul Erdős y Ronald Graham demostraron que un embalaje inclinado más inteligente podría dejar un área significativamente más pequeña, [ 19] Roth y Bob Vaughan respondieron con un artículo de 1978 que demostraba el primer límite inferior no trivial del problema. Como mostraron, para algunos valores de , el área descubierta debe ser al menos proporcional a . [2] [20]
En 1966, Heini Halberstam y Roth publicaron su libro Sequences , sobre secuencias enteras . Inicialmente planeado para ser el primero de un conjunto de dos volúmenes, sus temas incluían las densidades de sumas de secuencias, límites en el número de representaciones de números enteros como sumas de miembros de secuencias, densidad de secuencias cuyas sumas representan todos los números enteros, teoría de tamices y el método probabilístico , y secuencias en las que ningún elemento es múltiplo de otro . [21] Se publicó una segunda edición en 1983. [22]

Roth ganó la Medalla Fields en 1958 por su trabajo sobre la aproximación diofántica. Fue el primer medallista de British Fields. [1] Fue elegido miembro de la Royal Society en 1960 y más tarde se convirtió en miembro honorario de la Royal Society de Edimburgo , miembro del University College London, miembro del Imperial College London y miembro honorario de Peterhouse. [1] Para él era motivo de diversión que su Medalla Fields, su elección a la Royal Society y su cátedra le llegaran en orden inverso a su prestigio. [2]
La Sociedad Matemática de Londres le otorgó a Roth la Medalla De Morgan en 1983. [3] En 1991, la Sociedad Real le otorgó su Medalla Sylvester "por sus numerosas contribuciones a la teoría de números y, en particular, su solución del famoso problema relativo a la aproximación de números algebraicos mediante racionales". ". [23]
En 2009, en honor al 80 cumpleaños de Roth, se publicó un festival de 32 ensayos sobre temas relacionados con la investigación de Roth, [24] y en 2017 los editores de la revista Mathematika dedicaron un número especial a Roth. [25] Después de la muerte de Roth, el Departamento de Matemáticas del Imperial College instituyó la Beca Roth en su honor. [26]
{{cite journal}}: Mantenimiento CS1: publicación periódica sin título ( enlace ){{cite journal}}: Mantenimiento CS1: publicación periódica sin título ( enlace ){{cite journal}}: Mantenimiento CS1: publicación periódica sin título ( enlace ){{cite journal}}: Mantenimiento CS1: publicación periódica sin título ( enlace )