
En teoría musical , una inversión es una reorganización de los elementos de arriba hacia abajo en un intervalo, un acorde, una melodía o un grupo de líneas contrapuntísticas de música. [2] En cada uno de estos casos, "inversión" tiene un significado distinto pero relacionado. El concepto de inversión también juega un papel importante en la teoría de conjuntos musicales .
Un intervalo se invierte subiendo o bajando cualquiera de las notas una o más octavas, de modo que la nota más alta se convierta en la nota más baja y viceversa. Por ejemplo, la inversión de un intervalo que consta de un do con un mi encima (el tercer compás siguiente) es un mi con un do encima; para calcularlo, se puede subir el do, bajar el mi o mover ambos.

Las tablas de la derecha muestran los cambios en la calidad y el número de intervalos bajo inversión. Así, los intervalos perfectos siguen siendo perfectos, los intervalos mayores se convierten en menores y viceversa, y los intervalos aumentados se reducen y viceversa. (Los intervalos doblemente disminuidos se convierten en intervalos doblemente aumentados y viceversa.)
Los números de intervalos tradicionales suman nueve: los segundos se convierten en séptimas y viceversa, los tercios en sextas y viceversa, y así sucesivamente. Así, una cuarta justa se convierte en una quinta justa, una cuarta aumentada en una quinta disminuida y un intervalo simple (es decir, uno que es más estrecho que una octava) y su inversión, cuando se suman, dan como resultado una octava. Véase también complemento (música) .

La inversión de un acorde describe la relación de sus notas más bajas con las demás notas del acorde. Por ejemplo, una tríada en do mayor contiene los tonos do, mi y sol; su inversión está determinada por cuál de estos tonos es la nota más baja (o nota grave ) del acorde.
El término inversión se suele utilizar para referirse a las distintas posibilidades, aunque también puede restringirse a aquellos acordes en los que la nota más baja no es también la fundamental del acorde. Los textos que siguen esta restricción pueden utilizar el término posición para referirse a todas las posibilidades como categoría.
Un acorde está en posición fundamental si su fundamental es la nota más baja. A veces, se lo conoce como el acorde padre de sus inversiones. Por ejemplo, la fundamental de una tríada en Do mayor es Do, por lo que una tríada en Do mayor estará en posición fundamental si Do es la nota más baja y su tercera y quinta (Mi y Sol, respectivamente) están por encima de ella o, en ocasiones, no suenan en absoluto.
Las siguientes tríadas en Do mayor están en posición fundamental , ya que la nota más baja es la fundamental. La reorganización de las notas por encima del bajo en diferentes octavas (aquí, la nota Mi) y la duplicación de notas (aquí, Sol) se conoce como sonorización : la primera sonorización es cerrada , mientras que la segunda es abierta .

En un acorde invertido, la nota fundamental no es la nota más baja. Las inversiones se numeran en el orden en que aparecen las notas más bajas en un acorde con posición fundamental cercana (de abajo hacia arriba).

Como se muestra arriba, una tríada en do mayor (o cualquier acorde con tres notas) tiene dos inversiones:
Los acordes con cuatro notas (como los acordes de séptima ) funcionan de manera similar, excepto que tienen tres inversiones, en lugar de solo dos. Las tres inversiones de un acorde de séptima dominante de sol son:
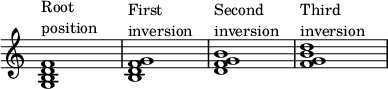
El bajo cifrado es una notación en la que las inversiones de acordes se indican con números arábigos (las cifras ) ya sea por encima o por debajo de las notas graves , lo que indica una progresión armónica . Cada número expresa el intervalo que resulta de las voces por encima de él (generalmente asumiendo la equivalencia de octava ). Por ejemplo, en la tríada de posición fundamental C–E–G, los intervalos por encima de la nota grave C son una tercera y una quinta, lo que da las cifras5
3Si esta tríada estuviera en primera inversión (por ejemplo, E–G–C), la figura6
3se aplicaría, debido a los intervalos de tercera y sexta que aparecen encima de la nota grave E.
Existen ciertas abreviaturas convencionales en el uso del bajo cifrado. Por ejemplo, las tríadas de posición fundamental aparecen sin símbolos (la5
3se entiende), y las tríadas de primera inversión se abrevian habitualmente como simplemente 6 , en lugar de6
3La tabla de la derecha muestra estas convenciones.
Los números de bajo cifrado expresan intervalos distintos en un acorde solo en relación con la nota grave. No hacen referencia a la tonalidad de la progresión (a diferencia del análisis armónico con números romanos ), no expresan intervalos entre pares de voces superiores en sí mismos (por ejemplo, en una tríada C-E-G, el bajo cifrado no indica la relación de intervalo entre E-G) y no expresan notas en voces superiores que duplican o están al unísono con la nota grave.
Sin embargo, las figuras se utilizan a menudo solas (sin el bajo) en la teoría musical simplemente para especificar la inversión de un acorde. Esta es la base de los términos dados anteriormente, como "6
4acorde " para una tríada de segunda inversión. De manera similar, en el análisis armónico el término I 6 se refiere a una tríada tónica en primera inversión.
Una notación para la inversión de acordes que se usa a menudo en la música popular es escribir el nombre de un acorde seguido de una barra inclinada y luego el nombre de la nota del bajo. [4] Esto se llama acorde de barra inclinada . Por ejemplo, un acorde de Do mayor en primera inversión (es decir, con Mi en el bajo) se notaría como "Do/Mi". Esta notación funciona incluso cuando una nota que no está presente en una tríada es el bajo; por ejemplo, F/G [5] es una forma de notar un enfoque particular para sonorizar un acorde Fadd 9 (G–F–A–C). Esto es bastante diferente de las notaciones analíticas de función ; por ejemplo, la notación "IV/V" representa la subdominante de la dominante .
Las letras minúsculas se pueden colocar después de un símbolo de acorde para indicar la posición fundamental o inversión. [6] [ página necesaria ] Por lo tanto, en la tonalidad de Do mayor, un acorde de Do mayor en primera inversión se puede notar como Ib , indicando el acorde I, primera inversión . (Con menos frecuencia, se nombra la raíz del acorde, seguida de una letra minúscula: Cb ). Si no se agrega ninguna letra, se asume que el acorde está en inversión fundamental, como si se hubiera insertado una a .
En el Tratado de armonía de Jean-Philippe Rameau (1722), los acordes en diferentes inversiones se consideran funcionalmente equivalentes y se le atribuye el mérito de ser la primera persona en reconocer su similitud subyacente. [7] [8] Los teóricos anteriores hablaban de diferentes intervalos utilizando descripciones alternativas, como la regola delle terze e seste ("regla de sextas y terceras"). Esto requería la resolución de consonancias imperfectas en perfectas y no propondría, por ejemplo, una semejanza entre6
4y5
3acordes.

En la inversión contrapuntística , dos melodías , que previamente se habían acompañado una a la otra, se acompañan de nuevo pero con la melodía que había estado en la voz aguda ahora en la grave, y viceversa. La acción de cambiar las voces se llama inversión textural . Esto se llama doble contrapunto cuando intervienen dos voces y triple contrapunto cuando intervienen tres. La inversión en el contrapunto invertible a dos voces también se conoce como rivolgimento . [9]
Los temas que pueden desarrollarse de esta manera sin violar las reglas del contrapunto se dicen que están en contrapunto invertible . El contrapunto invertible puede ocurrir en varios intervalos, generalmente en la octava , con menos frecuencia en la décima o duodécima . Para calcular el intervalo de inversión, [ aclaración necesaria ] suma los intervalos por los que se ha movido cada voz y resta uno. Por ejemplo: si el motivo A en la voz alta baja una sexta, y el motivo B en la voz baja sube una quinta, de tal manera que da como resultado que A y B hayan intercambiado registros, entonces los dos están en doble contrapunto en la décima (6 + 5 – 1 = 10).
En El arte de la fuga de J. S. Bach , el primer canon está en la octava, el segundo en la décima, el tercer canon en la duodécima y el cuarto canon en aumento y movimiento contrario. Se pueden encontrar otros ejemplos en las fugas en sol menor Archivado el 27 de marzo de 2010 en Wayback Machine y en si bemol mayor [películas Shockwave externas] de El clave bien temperado de J. S. Bach , libro 2, que contienen contrapunto invertible en la octava, la décima y la duodécima.
Por ejemplo, en el preludio para teclado en la bemol mayor de El clave bien temperado , Libro 1, de J. S. Bach, el siguiente pasaje, de los compases 9 al 18, incluye dos líneas, una en cada mano:

Cuando este pasaje regresa en los compases 25-35 se intercambian estos versos:

La Invención a tres voces en fa menor, BWV 795 de JS Bach implica la exploración de la combinación de tres temas. Dos de ellos se anuncian en los dos primeros compases. Una tercera idea los une en los compases 3 y 4. Cuando este pasaje se repite unos compases más adelante en los compases 7 a 9, las tres partes se intercambian:

La pieza continúa explorando cuatro de las seis posibles permutaciones de cómo estas tres líneas pueden combinarse en contrapunto.
Uno de los ejemplos más espectaculares de contrapunto invertible se da en el final de la Sinfonía Júpiter de Mozart . En él se escuchan nada menos que cinco temas juntos:

Todo el pasaje concluye la sinfonía con un destello de brillante composición orquestal. Según Tom Service :
La composición del final de la Sinfonía Júpiter por parte de Mozart es un palimpsesto de la historia de la música y de la suya propia. Como logro musical, su predecesor más obvio es en realidad el final fugado de su Cuarteto de cuerdas en sol mayor K. 387 , pero este final sinfónico supera incluso a esa pieza en su escala y ambición. Si la historia del primer movimiento de esa melodía operística es convertir la emoción instintiva en experiencia contrapuntística, el final hace exactamente lo contrario, transmutando las artes más complejas del oficio de composición en un sentimiento puro y estimulante. Sus modelos en Michael y Joseph Haydn son incuestionables, pero Mozart al mismo tiempo les rinde homenaje y los trasciende. Eso es lo que yo llamo verdadera originalidad. [10]


Una melodía se invierte dándole la vuelta, invirtiendo así su contorno . Por ejemplo, si la melodía original tiene una tercera mayor ascendente , la melodía invertida tiene una tercera mayor descendente (o, especialmente en la música tonal , quizás una tercera menor descendente ).
Según el Diccionario de música de Harvard , "los intervalos entre tonos sucesivos pueden permanecer exactos o, más a menudo en la música tonal, pueden ser equivalentes en la escala diatónica . Por lo tanto, do'–re–mi' puede convertirse en do'–si–la (donde el primer descenso es de un semitono en lugar de un tono entero) en lugar de do'–si ♭ –la ♭ ". [11] Además, la inversión puede comenzar en el mismo tono que la melodía original, pero no tiene por qué hacerlo, como lo ilustra el ejemplo de la derecha.
En la técnica dodecafónica , la inversión de una fila de tonos es una de sus cuatro permutaciones tradicionales (las otras son la forma principal , la retrógrada y la inversión retrógrada ). Estas cuatro permutaciones (etiquetadas como principal , retrógrada , inversión e inversión retrógrada ) para la fila de tonos utilizada en las Variaciones para orquesta, Op. 31, de Arnold Schoenberg se muestran a continuación.

En la teoría de conjuntos , la operación inversa a veces se designa como , donde significa "invertir" y significa "transponer por algún intervalo " medido en número de semitonos . Por lo tanto, la inversión es una combinación de una inversión seguida de una transposición . Para aplicar la operación de inversión , se resta la clase de tono , en notación entera , de 12 (por convención, la inversión es alrededor de la clase de tono 0). Luego aplicamos la operación de transposición sumando . Por ejemplo, para calcular , primero restamos 3 de 12 (dando 9) y luego sumamos 5 (dando 14, que es equivalente a 2). Por lo tanto, . [12] Para invertir un conjunto de tonos, simplemente invierte cada tono en el conjunto por turno. [13]
En teoría de conjuntos, la equivalencia inversional es el concepto de que los intervalos , acordes y otros conjuntos de tonos son iguales cuando se invierten. [ cita requerida ] Es similar a la equivalencia enarmónica , la equivalencia de octava e incluso la equivalencia transposicional . La equivalencia inversional se utiliza poco en la teoría tonal , aunque se supone que los conjuntos que se pueden invertir entre sí son remotamente comunes. Sin embargo, solo se supone que son idénticos o casi idénticos en la teoría de conjuntos musicales.
Se dice que los conjuntos son inversamente simétricos si se proyectan sobre sí mismos bajo inversión. El tono alrededor del cual se deben invertir los conjuntos se dice que es el eje de simetría (o centro). Un eje puede estar en un tono específico o a medio camino entre dos tonos (suponiendo que no se utilizan microtonos ). Por ejemplo, el conjunto C–E ♭ –E–F ♯ –G–B ♭ tiene un eje en F, y un eje, a un tritono de distancia, en B si el conjunto está listado como F ♯ –G–B ♭ –C–E ♭ –E. Como otro ejemplo, el conjunto C–E–F–F ♯ –G–B tiene un eje en la díada F/F ♯ y un eje en B/C si está listado como F ♯ –G–B–C–E–F. [14]





En la teoría del jazz , un eje tonal es el centro alrededor del cual se invierte una melodía. [15]
El "eje de altura" funciona en el contexto de la operación compuesta de inversión transposicional, donde la transposición se lleva a cabo después de la inversión. Sin embargo, a diferencia de la teoría de conjuntos, la transposición puede ser cromática o diatónica . Por lo tanto, si se invierte DAG (P5 arriba, M2 abajo) a DGA (P5 abajo, M2 arriba) el "eje de altura" es D. Sin embargo, si se invierte a CFG el eje de altura es G mientras que si el eje de altura es A, la melodía se invierte a EAB.
La notación de la posición de octava puede determinar cuántas líneas y espacios parecen compartir el eje. El eje de tonos de DAG y su inversión ADE parecen estar entre C/B ♮ o el tono único F.
La inversión de las partes en el contrapunto invertible a dos voces.