El método de Horner

Algoritmo para la evaluación de polinomios

En matemáticas y ciencias de la computación , el método de Horner (o esquema de Horner ) es un algoritmo para la evaluación de polinomios . Aunque lleva el nombre de William George Horner , este método es mucho más antiguo, ya que el propio Horner lo ha atribuido a Joseph-Louis Lagrange , y se remonta a muchos cientos de años atrás, a los matemáticos chinos y persas. ^[1] Después de la introducción de las computadoras, este algoritmo se volvió fundamental para calcular de manera eficiente con polinomios.

El algoritmo se basa en la regla de Horner , en la que un polinomio se escribe en forma anidada : $${\displaystyle {\begin{aligned}&a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\={}&a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}.\end{aligned}}}$$

Esto permite la evaluación de un polinomio de grado n con solo multiplicaciones y sumas. Esto es óptimo, ya que hay polinomios de grado n que no se pueden evaluar con menos operaciones aritméticas. ^[2] ${\displaystyle n}$ ${\displaystyle n}$

Alternativamente, el método de Horner yEl método de Horner-Ruffini también se refiere a un método para aproximar las raíces de polinomios, descrito por Horner en 1819. Es una variante delmétodo de Newton-Raphsonque se volvió más eficiente para el cálculo manual mediante la aplicación de la regla de Horner. Fue ampliamente utilizado hasta que las computadoras comenzaron a usarse de manera generalizada alrededor de 1970.

Evaluación de polinomios y división larga

Dado el polinomio donde son coeficientes constantes, el problema es evaluar el polinomio en un valor específico de $${\displaystyle p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},}$$ ${\displaystyle a_{0},\ldots ,a_{n}}$ ${\displaystyle x_{0}}$ ${\displaystyle x.}$

Para ello se define recursivamente una nueva secuencia de constantes de la siguiente manera:

Entonces el valor de es . ${\displaystyle b_{0}}$ ${\displaystyle p(x_{0})}$

Para ver por qué funciona esto, el polinomio se puede escribir en la forma $${\displaystyle p(x)=a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}\ .}$$

Así, sustituyendo iterativamente en la expresión, ${\displaystyle b_{i}}$ $${\displaystyle {\begin{aligned}p(x_{0})&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}(a_{n-1}+b_{n}x_{0})\cdots {\big )}{\Big )}\\&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}b_{n-1}{\big )}{\Big )}\\&~~\vdots \\&=a_{0}+x_{0}b_{1}\\&=b_{0}.\end{aligned}}}$$

Ahora bien, se puede demostrar que;

Esta expresión constituye la aplicación práctica de Horner, ya que ofrece una forma muy rápida de determinar el resultado de; donde (que es igual a ) es el resto de la división, como se demuestra con los ejemplos siguientes. Si es una raíz de , entonces (lo que significa que el resto es ), lo que significa que se puede factorizar como . $${\displaystyle p(x)/(x-x_{0})}$$ ${\displaystyle b_{0}}$ ${\displaystyle p(x_{0})}$ ${\displaystyle x_{0}}$ ${\displaystyle p(x)}$ ${\displaystyle b_{0}=0}$ ${\displaystyle 0}$ ${\displaystyle p(x)}$ ${\displaystyle x-x_{0}}$

Para encontrar los valores consecutivos, se comienza determinando , que es simplemente igual a . Luego se trabaja recursivamente utilizando la fórmula: hasta llegar a . ${\displaystyle b}$ ${\displaystyle b_{n}}$ ${\displaystyle a_{n}}$ $${\displaystyle b_{n-1}=a_{n-1}+b_{n}x_{0}}$$ ${\displaystyle b_{0}}$

Ejemplos

Evaluar para . ${\displaystyle f(x)=2x^{3}-6x^{2}+2x-1}$ ${\displaystyle x=3}$

Utilizamos la división sintética de la siguiente manera:

 x0 │x3x2x1x0​ ​​ ​​ ​​ ​​ 3 │ 2 −6 2 −1 │ 6 0 6 └──────────────────────── 2 0 2 5

Las entradas de la tercera fila son la suma de las de las dos primeras. Cada entrada de la segunda fila es el producto del valor x (3 en este ejemplo) con la entrada de la tercera fila inmediatamente a la izquierda. Las entradas en la primera fila son los coeficientes del polinomio que se evaluará. Entonces, el resto de la división por es ${\displaystyle f(x)}$ ${\displaystyle x-3}$5 .

Pero por el teorema del resto polinomial , sabemos que el resto es . Por lo tanto, . ${\displaystyle f(3)}$ ${\displaystyle f(3)=5}$

En este ejemplo, si podemos ver que , las entradas en la tercera fila. Por lo tanto, la división sintética (que en realidad fue inventada y publicada por Ruffini 10 años antes de la publicación de Horner) es más fácil de usar; se puede demostrar que es equivalente al método de Horner. ${\displaystyle a_{3}=2,a_{2}=-6,a_{1}=2,a_{0}=-1}$ ${\displaystyle b_{3}=2,b_{2}=0,b_{1}=2,b_{0}=5}$

Como consecuencia del teorema del resto polinómico, las entradas en la tercera fila son los coeficientes del polinomio de segundo grado, el cociente de al dividir por . El resto es ${\displaystyle f(x)}$ ${\displaystyle x-3}$5. Esto hace que el método de Horner sea útil para la división larga de polinomios .

Dividir por : ${\displaystyle x^{3}-6x^{2}+11x-6}$ ${\displaystyle x-2}$

2 │ 1 −6 11 −6 │ 2 −8 6 └──────────────────────── 1 −4 3 0

El cociente es . ${\displaystyle x^{2}-4x+3}$

Sea y . Dividamos utilizando el método de Horner. ${\displaystyle f_{1}(x)=4x^{4}-6x^{3}+3x-5}$ ${\displaystyle f_{2}(x)=2x-1}$ ${\displaystyle f_{1}(x)}$ ${\displaystyle f_{2}\,(x)}$

 0,5 │ 4 −6 0 3 −5 │ 2 −2 −1 1 └─────────────────────── 2 −2 −1 1 −4

La tercera fila es la suma de las dos primeras filas, dividida por2. Cada entrada en la segunda fila es el producto de1 con la entrada de la tercera fila a la izquierda. La respuesta es $${\displaystyle {\frac {f_{1}(x)}{f_{2}(x)}}=2x^{3}-2x^{2}-x+1-{\frac {4}{2x-1}}.}$$

Eficiencia

La evaluación mediante la forma monomial de un polinomio de grado requiere, como máximo, sumas y multiplicaciones, si las potencias se calculan mediante multiplicaciones repetidas y cada monomio se evalúa individualmente. El costo se puede reducir a sumas y multiplicaciones evaluando las potencias de por iteración. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle (n^{2}+n)/2}$ ${\displaystyle n}$ ${\displaystyle 2n-1}$ ${\displaystyle x}$

Si los datos numéricos se representan en términos de dígitos (o bits), entonces el algoritmo ingenuo también implica almacenar aproximadamente veces el número de bits de : el polinomio evaluado tiene una magnitud aproximada de , y uno también debe almacenarse a sí mismo. Por el contrario, el método de Horner requiere solo adiciones y multiplicaciones, y sus requisitos de almacenamiento son solo veces el número de bits de . Alternativamente, el método de Horner se puede calcular con multiplicaciones-sumas fusionadas . El método de Horner también se puede extender para evaluar las primeras derivadas del polinomio con adiciones y multiplicaciones. ^[3] ${\displaystyle 2n}$ ${\displaystyle x}$ ${\displaystyle x^{n}}$ ${\displaystyle x^{n}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle kn}$

El método de Horner es óptimo, en el sentido de que cualquier algoritmo para evaluar un polinomio arbitrario debe utilizar al menos tantas operaciones como sea necesario. Alexander Ostrowski demostró en 1954 que el número de adiciones necesarias es mínimo. ^[4] Victor Pan demostró en 1966 que el número de multiplicaciones es mínimo. ^[5] Sin embargo, cuando es una matriz, el método de Horner no es óptimo . ${\displaystyle x}$

Esto supone que el polinomio se evalúa en forma monomial y no se permite ningún preacondicionamiento de la representación, lo que tiene sentido si el polinomio se evalúa solo una vez. Sin embargo, si se permite el preacondicionamiento y el polinomio se evaluará muchas veces, entonces son posibles algoritmos más rápidos . Implican una transformación de la representación del polinomio. En general, un polinomio de grado 1 se puede evaluar utilizando solo ⌊ n /2 ⌋ +2 multiplicaciones y sumas. ^[6] ${\displaystyle n}$ ${\displaystyle n}$

Evaluación paralela

Una desventaja de la regla de Horner es que todas las operaciones dependen secuencialmente , por lo que no es posible aprovechar el paralelismo a nivel de instrucción en las computadoras modernas. En la mayoría de las aplicaciones donde importa la eficiencia de la evaluación de polinomios, se evalúan simultáneamente muchos polinomios de orden bajo (para cada píxel o polígono en gráficos de computadora, o para cada cuadrado de la cuadrícula en una simulación numérica), por lo que no es necesario encontrar paralelismo dentro de una sola evaluación de polinomios.

Sin embargo, si uno está evaluando un solo polinomio de orden muy alto, puede ser útil dividirlo de la siguiente manera: $${\displaystyle {\begin{aligned}p(x)&=\sum _{i=0}^{n}a_{i}x^{i}\\[1ex]&=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\[1ex]&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+\left(a_{1}x+a_{3}x^{3}+a_{5}x^{5}+\cdots \right)\\[1ex]&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+x\left(a_{1}+a_{3}x^{2}+a_{5}x^{4}+\cdots \right)\\[1ex]&=\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i}x^{2i}+x\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i+1}x^{2i}\\[1ex]&=p_{0}(x^{2})+xp_{1}(x^{2}).\end{aligned}}}$$

En términos más generales, la suma se puede dividir en k partes: donde las sumas internas se pueden evaluar utilizando instancias paralelas separadas del método de Horner. Esto requiere un poco más de operaciones que el método básico de Horner, pero permite la ejecución SIMD de k vías de la mayoría de ellas. Los compiladores modernos generalmente evalúan polinomios de esta manera cuando es ventajoso, aunque para cálculos de punto flotante esto requiere habilitar matemáticas reasociativas (inseguras) ^{[ cita requerida ]} . $${\displaystyle p(x)=\sum _{i=0}^{n}a_{i}x^{i}=\sum _{j=0}^{k-1}x^{j}\sum _{i=0}^{\lfloor n/k\rfloor }a_{ki+j}x^{ki}=\sum _{j=0}^{k-1}x^{j}p_{j}(x^{k})}$$

Aplicación a la multiplicación y división de coma flotante

El método de Horner es un método rápido y eficiente en el uso del código para la multiplicación y división de números binarios en un microcontrolador sin multiplicador de hardware . Uno de los números binarios que se van a multiplicar se representa como un polinomio trivial, donde (usando la notación anterior) , y . Luego, x (o x elevado a alguna potencia) se factoriza repetidamente. En este sistema de numeración binario (base 2), , por lo que las potencias de 2 se factorizan repetidamente. ${\displaystyle a_{i}=1}$ ${\displaystyle x=2}$ ${\displaystyle x=2}$

Ejemplo

Por ejemplo, para encontrar el producto de dos números (0,15625) y m : $${\displaystyle {\begin{aligned}(0.15625)m&=(0.00101_{b})m=\left(2^{-3}+2^{-5}\right)m=\left(2^{-3})m+(2^{-5}\right)m\\&=2^{-3}\left(m+\left(2^{-2}\right)m\right)=2^{-3}\left(m+2^{-2}(m)\right).\end{aligned}}}$$

Método

Para encontrar el producto de dos números binarios d y m :

1. Un registro que contiene el resultado intermedio se inicializa en d .
2. Comience con el bit menos significativo (más a la derecha) distinto de cero en m .
   2. Cuenta (hacia la izquierda) la cantidad de posiciones de bit hasta el siguiente bit más significativo distinto de cero. Si no hay bits más significativos, toma el valor de la posición de bit actual.
   3. Usando ese valor, realice una operación de desplazamiento a la izquierda por esa cantidad de bits en el registro que contiene el resultado intermedio.
3. Si se contaron todos los bits distintos de cero, el registro de resultado intermedio ahora contiene el resultado final. De lo contrario, agregue d al resultado intermedio y continúe en el paso 2 con el siguiente bit más significativo en m .

Derivación

En general, para un número binario con valores de bit ( ) el producto es En esta etapa del algoritmo, se requiere que se eliminen los términos con coeficientes de valor cero, de modo que solo se cuenten los coeficientes binarios iguales a uno, por lo que el problema de la multiplicación o división por cero no es un problema, a pesar de esta implicación en la ecuación factorizada: ${\displaystyle d_{3}d_{2}d_{1}d_{0}}$ $${\displaystyle (d_{3}2^{3}+d_{2}2^{2}+d_{1}2^{1}+d_{0}2^{0})m=d_{3}2^{3}m+d_{2}2^{2}m+d_{1}2^{1}m+d_{0}2^{0}m.}$$ $${\displaystyle =d_{0}\left(m+2{\frac {d_{1}}{d_{0}}}\left(m+2{\frac {d_{2}}{d_{1}}}\left(m+2{\frac {d_{3}}{d_{2}}}(m)\right)\right)\right).}$$

Todos los denominadores son iguales a uno (o el término está ausente), por lo que esto se reduce a o de manera equivalente (como es consistente con el "método" descrito anteriormente) $${\displaystyle =d_{0}(m+2{d_{1}}(m+2{d_{2}}(m+2{d_{3}}(m)))),}$$ $${\displaystyle =d_{3}(m+2^{-1}{d_{2}}(m+2^{-1}{d_{1}}(m+{d_{0}}(m)))).}$$

En matemáticas binarias (base 2), la multiplicación por una potencia de 2 es simplemente una operación de desplazamiento de registro . Por lo tanto, la multiplicación por 2 se calcula en base 2 mediante un desplazamiento aritmético . El factor (2 ⁻¹ ) es un desplazamiento aritmético a la derecha , un (0) no da como resultado ninguna operación (ya que 2 ^{0 = 1 es el} elemento de identidad multiplicativo ) y un (2 ¹ ) da como resultado un desplazamiento aritmético a la izquierda. El producto de la multiplicación ahora se puede calcular rápidamente utilizando solo operaciones de desplazamiento aritmético, suma y resta.

El método es particularmente rápido en procesadores que admiten una instrucción única de desplazamiento y adición-acumulación. En comparación con una biblioteca de punto flotante de C, el método de Horner sacrifica algo de precisión, sin embargo, nominalmente es 13 veces más rápido (16 veces más rápido cuando se utiliza la forma de " dígito con signo canónico " (CSD)) y utiliza solo el 20% del espacio de código. ^[7]

Otras aplicaciones

El método de Horner se puede utilizar para convertir entre diferentes sistemas numéricos posicionales (en cuyo caso x es la base del sistema numérico y los coeficientes a _i son los dígitos de la representación en base x de un número dado) y también se puede utilizar si x es una matriz , en cuyo caso la ganancia en eficiencia computacional es aún mayor. Sin embargo, para tales casos se conocen métodos más rápidos . ^[8]

Hallazgo de raíces polinómicas

Utilizando el algoritmo de división larga en combinación con el método de Newton , es posible aproximar las raíces reales de un polinomio. El algoritmo funciona de la siguiente manera. Dado un polinomio de grado cero, haga una estimación inicial tal que . Ahora repita los dos pasos siguientes: ${\displaystyle p_{n}(x)}$ ${\displaystyle n}$ ${\displaystyle z_{n}<z_{n-1}<\cdots <z_{1},}$ ${\displaystyle x_{0}}$ ${\displaystyle z_{1}<x_{0}}$

1. Utilizando el método de Newton , encuentre el cero más grande de usando la suposición . ${\displaystyle z_{1}}$ ${\displaystyle p_{n}(x)}$ ${\displaystyle x_{0}}$
2. Usando el método de Horner, divide para obtener . Regresa al paso 1 pero usa el polinomio y la estimación inicial . ${\displaystyle (x-z_{1})}$ ${\displaystyle p_{n-1}}$ ${\displaystyle p_{n-1}}$ ${\displaystyle z_{1}}$

Estos dos pasos se repiten hasta que se encuentran todos los ceros reales del polinomio. Si los ceros aproximados no son lo suficientemente precisos, los valores obtenidos se pueden utilizar como estimaciones iniciales para el método de Newton, pero utilizando el polinomio completo en lugar de los polinomios reducidos. ^[9]

Ejemplo

Cálculo de raíces polinómicas mediante el método de Horner

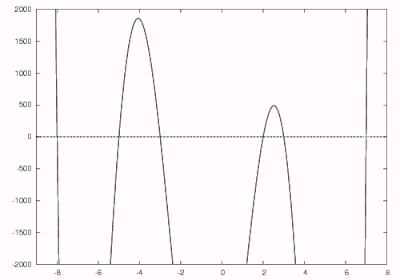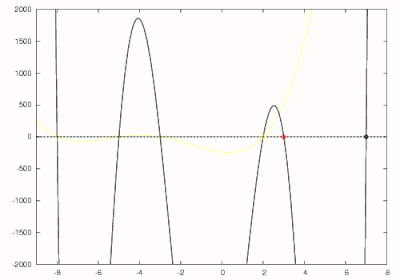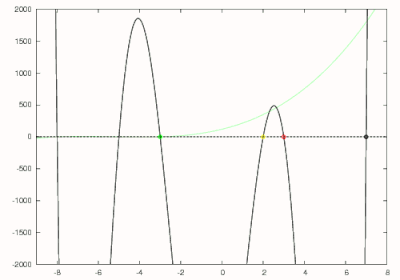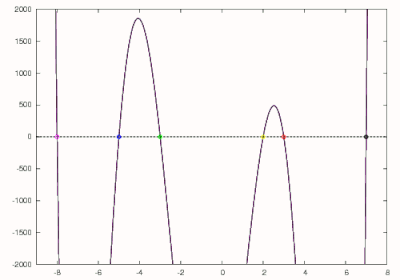
Considere el polinomio que se puede expandir a $${\displaystyle p_{6}(x)=(x+8)(x+5)(x+3)(x-2)(x-3)(x-7)}$$ $${\displaystyle p_{6}(x)=x^{6}+4x^{5}-72x^{4}-214x^{3}+1127x^{2}+1602x-5040.}$$

De lo anterior sabemos que la raíz más grande de este polinomio es 7, por lo que podemos hacer una estimación inicial de 8. Usando el método de Newton, el primer cero de 7 se encuentra como se muestra en negro en la figura de la derecha. Luego se divide por para obtener que se dibuja en rojo en la figura de la derecha. El método de Newton se usa para encontrar el cero más grande de este polinomio con una estimación inicial de 7. El cero más grande de este polinomio que corresponde al segundo cero más grande del polinomio original se encuentra en 3 y está rodeado en rojo. El polinomio de grado 5 ahora se divide por para obtener que se muestra en amarillo. El cero para este polinomio se encuentra en 2 nuevamente usando el método de Newton y está rodeado en amarillo. Ahora se usa el método de Horner para obtener que se muestra en verde y se encuentra que tiene un cero en −3. Este polinomio se reduce aún más a que se muestra en azul y produce un cero de −5. La raíz final del polinomio original se puede hallar utilizando el cero final como estimación inicial para el método de Newton o reduciendo y resolviendo la ecuación lineal . Como se puede observar, se hallaron las raíces esperadas de −8, −5, −3, 2, 3 y 7. ${\displaystyle p(x)}$ ${\displaystyle (x-7)}$ $${\displaystyle p_{5}(x)=x^{5}+11x^{4}+5x^{3}-179x^{2}-126x+720}$$ ${\displaystyle (x-3)}$ $${\displaystyle p_{4}(x)=x^{4}+14x^{3}+47x^{2}-38x-240}$$ $${\displaystyle p_{3}(x)=x^{3}+16x^{2}+79x+120}$$ $${\displaystyle p_{2}(x)=x^{2}+13x+40}$$ ${\displaystyle p_{2}(x)}$

Diferencia dividida de un polinomio

El método de Horner se puede modificar para calcular la diferencia dividida. Dado el polinomio (como antes), proceda de la siguiente manera ^[10] ${\displaystyle (p(y)-p(x))/(y-x).}$ $${\displaystyle p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},}$$ $${\displaystyle {\begin{aligned}b_{n}&=a_{n},&\quad d_{n}&=b_{n},\\b_{n-1}&=a_{n-1}+b_{n}x,&\quad d_{n-1}&=b_{n-1}+d_{n}y,\\&{}\ \ \vdots &\quad &{}\ \ \vdots \\b_{1}&=a_{1}+b_{2}x,&\quad d_{1}&=b_{1}+d_{2}y,\\b_{0}&=a_{0}+b_{1}x.\end{aligned}}}$$

Al finalizar, tenemos Este cálculo de la diferencia dividida está sujeto a un menor error de redondeo que evaluar y por separado, particularmente cuando . Sustituyendo en este método se obtiene , la derivada de . $${\displaystyle {\begin{aligned}p(x)&=b_{0},\\{\frac {p(y)-p(x)}{y-x}}&=d_{1},\\p(y)&=b_{0}+(y-x)d_{1}.\end{aligned}}}$$ ${\displaystyle p(x)}$ ${\displaystyle p(y)}$ ${\displaystyle x\approx y}$ ${\displaystyle y=x}$ ${\displaystyle d_{1}=p'(x)}$ ${\displaystyle p(x)}$

Historia

El algoritmo de Qin Jiushao para resolver la ecuación polinómica cuadrática da como resultado: x = 840 ^[11] ${\displaystyle -x^{4}+763200x^{2}-40642560000=0}$

El artículo de Horner, titulado "Un nuevo método para resolver ecuaciones numéricas de todos los órdenes, mediante aproximación continua", ^[12] fue leído ante la Royal Society de Londres, en su reunión del 1 de julio de 1819, con una secuela en 1823. ^[12] El artículo de Horner en la Parte II de Philosophical Transactions of the Royal Society of London de 1819 fue recibido calurosamente y expansivamente por un crítico ^{[ enlace muerto permanente ]} en el número de The Monthly Review: or, Literary Journal de abril de 1820; en comparación, un artículo técnico de Charles Babbage es rechazado bruscamente en esta reseña. La secuencia de reseñas en The Monthly Review de septiembre de 1821 concluye que Holdred fue la primera persona en descubrir una solución práctica directa y general de ecuaciones numéricas. Fuller ^[13] demostró que el método del artículo de Horner de 1819 difiere de lo que posteriormente se conoció como "método de Horner" y que, en consecuencia, la prioridad de este método debería recaer en Holdred (1820).

A diferencia de sus contemporáneos ingleses, Horner se basó en la literatura continental, en particular en la obra de Arbogast . También se sabe que Horner leyó atentamente el libro de álgebra de John Bonneycastle, aunque descuidó el trabajo de Paolo Ruffini .

Aunque a Horner se le atribuye haber hecho accesible y práctico el método, éste ya se conocía mucho antes que él. En orden cronológico inverso, el método de Horner ya se conocía por:

• Paolo Ruffini en 1809 (ver regla de Ruffini ) ^{[14] [15]}
• Isaac Newton en 1669 ^{[16] [17]}
• El matemático chino Zhu Shijie en el siglo XIV ^[15]
• El matemático chino Qin Jiushao en su Tratado matemático en nueve secciones del siglo XIII
• el matemático persa Sharaf al-Dīn al-Ṭūsī en el siglo XII (el primero en utilizar ese método en un caso general de ecuación cúbica) ^[18]
• El matemático chino Jia Xian en el siglo XI ( dinastía Song )
• Los nueve capítulos sobre el arte matemático , obra china de la dinastía Han (202 a. C. – 220 d. C.) editada por Liu Hui (hacia el siglo III a. C.). ^[19]

Qin Jiushao , en su Shu Shu Jiu Zhang ( Tratado matemático en nueve secciones ; 1247), presenta una serie de métodos de tipo Horner para resolver ecuaciones polinómicas, que se basaban en trabajos anteriores del matemático de la dinastía Song del siglo XI , Jia Xian ; por ejemplo, un método es específicamente adecuado para las biquinticas, de las que Qin da un ejemplo, de acuerdo con la costumbre china de entonces de los estudios de casos. Yoshio Mikami en Development of Mathematics in China and Japan (Leipzig 1913) escribió:

"... ¿Quién puede negar el hecho de que el ilustre proceso de Horner se utilizó en China al menos casi seis siglos antes que en Europa? ... Por supuesto, no tenemos la intención de atribuir la invención de Horner a un origen chino, pero el lapso de tiempo suficientemente largo hace que no sea del todo imposible que los europeos pudieran haber conocido el método chino de manera directa o indirecta". ^[20]

Ulrich Libbrecht concluyó: Es obvio que este procedimiento es una invención china... el método no era conocido en la India . Dijo que Fibonacci probablemente lo aprendió de los árabes, quienes tal vez lo tomaron prestado de los chinos. ^[21] La extracción de raíces cuadradas y cúbicas siguiendo líneas similares ya fue discutida por Liu Hui en conexión con los Problemas IV.16 y 22 en Jiu Zhang Suan Shu , mientras que Wang Xiaotong en el siglo VII supone que sus lectores pueden resolver ecuaciones cúbicas mediante un método de aproximación descrito en su libro Jigu Suanjing .

Véase también

• Algoritmo de Clenshaw para evaluar polinomios en forma de Chebyshev
• Algoritmo de De Boor para evaluar splines en forma B-spline
• Algoritmo de De Casteljau para evaluar polinomios en forma de Bézier
• Esquema de Estrin para facilitar la paralelización en arquitecturas informáticas modernas
• Método de Lill para aproximar raíces gráficamente
• Regla de Ruffini y división sintética para dividir un polinomio por un binomio de la forma x − r

Notas

1. 600 años antes, por el matemático chino Qin Jiushao y 700 años antes, por el matemático persa Sharaf al-Dīn al-Ṭūsī
2. Pan 1966
3. Pankiewicz 1968.
4. Ostrowski 1954.
5. Pan 1966.
6. Knuth 1997.
7. Kripasagar 2008, pág. 62.
8. Higham 2002, Sección 5.4.
9. Kress 1991, pág. 112.
10. Fateman y Kahan 2000
11. Libbrecht 2005, págs. 181-191.
12. Horner 1819.
13. Fuller 1999, págs. 29–51.
14. Cajori 1911.
15. O'Connor, John J.; Robertson, Edmund F. , "El método de Horner", Archivo de Historia de las Matemáticas MacTutor , Universidad de St Andrews
16. Análisis por serie Quantitatum, Fluctiones ac Differentias: Cum Enumeratione Linearum Tertii Ordinis, Londini. Ex Officina Pearsoniana. Año MDCCXI, pág. 10, 4º párrafo.
17. Documentos recopilados de Newton, edición de 1779, en una nota al pie, vol. I, pág. 270-271
18. Berggren 1990, págs. 304–309.
19. Temple 1986, pág. 142.
20. Mikami 1913, pág. 77
21. Libbrecht 2005, pág. 208.

Referencias

• Berggren, JL (1990). "Innovación y tradición en Muadalat de Sharaf al-Din al-Tusi". Revista de la Sociedad Oriental Americana . 110 (2): 304–309. doi :10.2307/604533. JSTOR  604533.
• Cajori, Florian (1911). «El método de aproximación de Horner anticipado por Ruffini». Boletín de la Sociedad Matemática Americana . 17 (8): 409–414. doi : 10.1090/s0002-9904-1911-02072-9 . Archivado desde el original el 4 de septiembre de 2017. Consultado el 4 de marzo de 2012 .Leído ante la Sección Suroeste de la Sociedad Matemática Americana el 26 de noviembre de 1910.
• Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein10.1016/0315-0860(81)90069-0, Clifford (2009). "Introducción a los algoritmos". Historia Matemática . 8 (3) (3ª ed.). Prensa del MIT: 277–318. doi : 10.1016/0315-0860(81)90069-0 .{{cite journal}}: CS1 maint: numeric names: authors list (link)
• Fateman, RJ ; Kahan, W. (2000). Improving exact integrals from symbolalgebra systems (PDF) (Informe). PAM. Universidad de California, Berkeley: Centro de Matemáticas Pura y Aplicada. Archivado desde el original (PDF) el 2017-08-14 . Consultado el 2018-05-17 .
• Fuller, AT (1999). "Horner versus Holdred: Un episodio en la historia del cálculo de raíces". Historia Mathematica . 26 : 29–51. doi : 10.1006/hmat.1998.2214 .
• Higham, Nicholas (2002). Precisión y estabilidad de algoritmos numéricos . SIAM. ISBN 978-0-89871-521-7.
• Holdred, T. (1820). Un nuevo método para resolver ecuaciones con facilidad y rapidez; por el cual se encuentra el valor verdadero de la cantidad desconocida sin reducción previa. Con un suplemento que contiene otros dos métodos para resolver ecuaciones, derivados del mismo principio (PDF) . Richard Watts. Archivado desde el original (PDF) el 2014-01-06 . Consultado el 2012-12-10 .

  El método de Holdred se encuentra en el suplemento que aparece después de la página 45 (que es la página 52 de la versión en pdf).

• Horner, William George (julio de 1819). "Un nuevo método para resolver ecuaciones numéricas de todos los órdenes, mediante aproximación continua". Philosophical Transactions . 109 . Royal Society of London: 308–335. doi :10.1098/rstl.1819.0023. JSTOR  107508. S2CID  186210512.

  Disponible directamente en línea a través del enlace, pero también reimpreso con evaluación en DE Smith: A Source Book in Mathematics , McGraw-Hill, 1929; reimpresión de Dover, 2 vols, 1959.

• Knuth, Donald (1997). El arte de la programación informática . Vol. 2: Algoritmos seminuméricos (3.ª ed.). Addison-Wesley. Págs. 486–488 en la sección 4.6.4. ISBN 978-0-201-89684-8.
• Kress, Rainer (1991). Análisis numérico . Springer.
• Kripasagar, Venkat (marzo de 2008). "Micromatemáticas eficientes: técnicas de multiplicación y división para microcontroladores". Revista Circuit Cellar (212).
• Libbrecht, Ulrich (2005). "Capítulo 13". Matemáticas chinas en el siglo XIII (2.ª ed.). Dover. ISBN 978-0-486-44619-6Archivado desde el original el 6 de junio de 2017. Consultado el 23 de agosto de 2016 .
• Mikami, Yoshio (1913). "Capítulo 11. Ch'in Chiu-Shao". El desarrollo de las matemáticas en China y Japón (1.ª ed.). Reimpresión de Chelsea Publishing Co., págs. 74-77.
• Ostrowski, Alexander M. (1954). "Sobre dos problemas de álgebra abstracta relacionados con la regla de Horner". Estudios de matemáticas y mecánica presentados a Richard von Mises . Academic Press. págs. 40–48. ISBN 978-1-4832-3272-0Archivado desde el original el 15 de abril de 2019. Consultado el 23 de agosto de 2016 .
• Pan, Y. Ja (1966). "Sobre los medios para calcular valores de polinomios". Russian Math. Surveys . 21 : 105–136. doi :10.1070/rm1966v021n01abeh004147. S2CID  250869179.
• Pankiewicz, W. (1968). "Algoritmo 337: cálculo de un polinomio y sus valores derivados mediante el esquema de Horner". Comunicaciones de la ACM . 11 (9). ACM: 633. doi : 10.1145/364063.364089 . S2CID  52859619.
• Spiegel, Murray R. (1956). Esquema de teoría y problemas de álgebra universitaria de Schaum . McGraw-Hill. ISBN 9780070602267.
• Temple, Robert (1986). El genio de China: 3.000 años de ciencia, descubrimiento e invención . Simon and Schuster. ISBN 978-0-671-62028-8.
• Whittaker, ET ; Robinson, G. (1924). El cálculo de las observaciones. Londres: Blackie.
• Wylie, Alexander (1897). "Apuntes sobre la ciencia de la aritmética china". Investigaciones chinas . Shanghái. págs. 159-194.{{cite book}}: CS1 maint: location missing publisher (link)

  Reimpreso de los números de The North China Herald (1852).

Enlaces externos

• "Esquema de Horner", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Qiu Jin-Shao, Shu Shu Jiu Zhang (Cong Shu Ji Cheng ed.)
• Para obtener más información sobre la aplicación de búsqueda de raíz, consulte [1] Archivado el 28 de septiembre de 2018 en Wayback Machine.