En matemáticas , el grupo ortogonal especial en tres dimensiones, también conocido como grupo de rotación SO(3) , es un ejemplo natural de variedad . Los diversos gráficos de SO(3) establecen sistemas de coordenadas rivales : en este caso, no se puede decir que exista un conjunto preferido de parámetros que describan una rotación. Hay tres grados de libertad , por lo que la dimensión de SO(3) es tres. En numerosas aplicaciones se utiliza uno u otro sistema de coordenadas, y surge la pregunta de cómo convertir de un sistema dado a otro.
En geometría, el grupo de rotación es el grupo de todas las rotaciones sobre el origen del espacio euclidiano tridimensional R 3 bajo la operación de composición . [1] Por definición, una rotación sobre el origen es una transformación lineal que preserva la longitud de los vectores (es una isometría ) y preserva la orientación (es decir, la lateralidad ) del espacio. Una transformación que preserva la longitud pero invierte la orientación se denomina rotación impropia . Cada rotación impropia del espacio euclidiano tridimensional es una rotación seguida de una reflexión en un plano que pasa por el origen.
La composición de dos rotaciones da como resultado otra rotación; cada rotación tiene una rotación inversa única; y la función identidad satisface la definición de rotación. Debido a las propiedades anteriores, el conjunto de todas las rotaciones es un grupo en composición. Además, el grupo de rotación tiene una estructura de variedad natural para la cual las operaciones del grupo son suaves ; por lo tanto, es de hecho un grupo de Lie . El grupo de rotación a menudo se denota SO(3) por las razones que se explican a continuación.
El espacio de rotaciones es isomorfo con el conjunto de operadores de rotación y el conjunto de matrices ortonormales con determinante +1. También está estrechamente relacionado ( doblemente cubierto ) con el conjunto de cuaterniones con su producto interno, así como con el conjunto de vectores de rotación (aunque aquí la relación es más difícil de describir, ver más abajo para más detalles), con una operación de composición interna diferente dada por el producto de sus matrices equivalentes.
La notación de vectores de rotación surge del teorema de rotación de Euler , que establece que cualquier rotación en tres dimensiones puede describirse mediante una rotación de un ángulo determinado sobre un eje. Teniendo esto en cuenta, podemos especificar el eje de una de estas rotaciones mediante dos ángulos y podemos utilizar el radio del vector para especificar el ángulo de rotación . Estos vectores representan una pelota en 3D con una topología inusual.
Esta esfera sólida 3D es equivalente a la superficie de un disco 4D, que también es una variedad 3D. Para realizar esta equivalencia, tendremos que definir cómo representaremos una rotación con esta superficie incrustada en 4D.
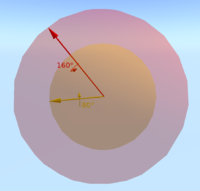
Es interesante considerar el espacio como la esfera tridimensional S 3 , el límite de un disco en el espacio euclidiano de cuatro dimensiones. Para ello, tendremos que definir cómo representamos una rotación con esta superficie incrustada en cuatro dimensiones.
La forma en que se puede utilizar el radio para especificar el ángulo de rotación no es sencilla. Se puede relacionar con círculos de latitud en una esfera con un polo norte definido y se explica de la siguiente manera:
Partiendo del polo norte de una esfera en el espacio tridimensional, especificamos el punto en el polo norte para representar la rotación identidad. En el caso de la rotación identidad, no se define ningún eje de rotación y el ángulo de rotación (cero) es irrelevante. Una rotación con su eje contenido en el plano xy y un ángulo de rotación muy pequeño se puede especificar mediante un corte a través de la esfera paralelo al plano xy y muy cerca del polo norte. El círculo definido por este corte será muy pequeño, correspondiente al pequeño ángulo de la rotación. A medida que los ángulos de rotación se hacen más grandes, el corte se mueve hacia el sur y los círculos se hacen más grandes hasta que se alcanza el ecuador de la esfera, que corresponderá a un ángulo de rotación de 180 grados. Continuando hacia el sur, los radios de los círculos ahora se hacen más pequeños (correspondientes al valor absoluto del ángulo de la rotación considerado como un número negativo). Finalmente, cuando se alcanza el polo sur, los círculos se encogen una vez más hasta la rotación identidad, que también se especifica como el punto en el polo sur. Observe que en esta visualización se pueden ver varias características de dichas rotaciones y sus representaciones.
El espacio de rotaciones es continuo, cada rotación tiene un vecindario de rotaciones que son casi iguales y este vecindario se vuelve plano a medida que se contrae.
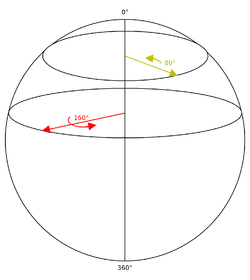
Además, cada rotación está representada en realidad por dos puntos antípodas en la esfera, que están en los extremos opuestos de una línea que pasa por el centro de la esfera. Esto refleja el hecho de que cada rotación puede representarse como una rotación sobre algún eje o, equivalentemente, como una rotación negativa sobre un eje que apunta en la dirección opuesta (una llamada doble cobertura ). La "latitud" de un círculo que representa un ángulo de rotación particular será la mitad del ángulo representado por esa rotación, ya que a medida que el punto se mueve del polo norte al polo sur, la latitud varía de cero a 180 grados, mientras que el ángulo de rotación varía de 0 a 360 grados . (la "longitud" de un punto representa entonces un eje de rotación particular). Nótese, sin embargo, que este conjunto de rotaciones no está cerrado bajo composición.
Dos rotaciones sucesivas con ejes en el plano xy no necesariamente darán como resultado una rotación cuyo eje se encuentre en el plano xy y, por lo tanto, no se puede representar como un punto en la esfera. Este no será el caso con una rotación general en el espacio tridimensional, que sí forma un conjunto cerrado bajo composición.
Esta visualización se puede extender a una rotación general en un espacio tridimensional. La rotación identidad es un punto, y un pequeño ángulo de rotación sobre algún eje se puede representar como un punto en una esfera con un radio pequeño. A medida que el ángulo de rotación crece, la esfera crece, hasta que el ángulo de rotación alcanza los 180 grados, momento en el que la esfera comienza a encogerse, convirtiéndose en un punto a medida que el ángulo se acerca a los 360 grados (o cero grados desde la dirección negativa). Este conjunto de esferas que se expanden y contraen representa una hiperesfera en un espacio tetradimensional (una 3-esfera).
Al igual que en el ejemplo más simple anterior, cada rotación representada como un punto en la hiperesfera se corresponde con su punto antípoda en esa hiperesfera. La "latitud" en la hiperesfera será la mitad del ángulo de rotación correspondiente, y la vecindad de cualquier punto se volverá "más plana" (es decir, estará representada por un espacio euclidiano tridimensional de puntos) a medida que la vecindad se encoge.
Este comportamiento se corresponde con el conjunto de cuaterniones unitarios : un cuaternión general representa un punto en un espacio de cuatro dimensiones, pero al restringirlo a una magnitud unitaria se obtiene un espacio tridimensional equivalente a la superficie de una hiperesfera. La magnitud del cuaternión unitario será la unidad, lo que corresponde a una hiperesfera de radio unitario.
La parte vectorial de un cuaternión unitario representa el radio de la 2-esfera correspondiente al eje de rotación, y su magnitud es el seno de la mitad del ángulo de rotación. Cada rotación está representada por dos cuaterniones unitarios de signo opuesto y, como en el espacio de rotaciones en tres dimensiones, el producto de cuaterniones de dos cuaterniones unitarios dará como resultado un cuaternión unitario. Además, el espacio de cuaterniones unitarios es "plano" en cualquier entorno infinitesimal de un cuaternión unitario dado.
Podemos parametrizar el espacio de rotaciones de varias maneras, pero siempre aparecerán degeneraciones. Por ejemplo, si utilizamos tres ángulos ( ángulos de Euler ), dicha parametrización se degenera en algunos puntos de la hiperesfera, lo que conduce al problema del bloqueo del cardán . Podemos evitarlo utilizando cuatro coordenadas euclidianas w , x , y , z , con w2 + x2 + y2 + z2 = 1 . El punto ( w , x , y , z ) representa una rotación alrededor del eje dirigido por el vector ( x , y , z ) por un ángulo
Este problema es similar a parametrizar la superficie bidimensional de una esfera con dos coordenadas, como latitud y longitud. La latitud y la longitud se comportan mal ( degeneran ) en los polos norte y sur, aunque los polos no son intrínsecamente diferentes de cualquier otro punto de la esfera. En los polos (latitudes +90° y −90°), la longitud deja de tener sentido. Se puede demostrar que ningún sistema de coordenadas de dos parámetros puede evitar tal degeneración.
Los posibles candidatos para parametrizaciones incluyen:
Existen problemas al utilizar estos como algo más que cartas locales, que tienen que ver con su naturaleza multivaluada y con las singularidades. Es decir, hay que tener cuidado sobre todo de trabajar sólo con difeomorfismos en la definición de carta . Problemas de este tipo son inevitables, ya que SO(3) es difeomorfo al espacio proyectivo real P 3 ( R ), que es un cociente de S 3 mediante la identificación de puntos antípodas, y las cartas intentan modelar una variedad utilizando R 3 .
Esto explica por qué, por ejemplo, los ángulos de Euler parecen dar una variable en el 3- toro y los cuaterniones unitarios en una 3-esfera . La unicidad de la representación por ángulos de Euler se rompe en algunos puntos (cf. bloqueo de cardán ), mientras que la representación de cuaterniones es siempre una doble cobertura , con q y − q dando la misma rotación.
Si usamos una matriz antisimétrica, cada matriz antisimétrica 3 × 3 está determinada por 3 parámetros, y por lo tanto, a primera vista, el espacio de parámetros es R 3 . Exponenciando tal matriz resulta en una matriz ortogonal 3 × 3 de determinante 1 – en otras palabras, una matriz de rotación, pero esta es una función de muchos a uno. Nótese que no es una función de recubrimiento – mientras que es un homeomorfismo local cerca del origen, no es una función de recubrimiento en rotaciones de 180 grados. Es posible restringir estas matrices a una bola alrededor del origen en R 3 de modo que las rotaciones no excedan los 180 grados, y esto será uno a uno, excepto para rotaciones de 180 grados, que corresponden al límite S 2 , y estos identifican puntos antípodas – este es el lugar geométrico de corte . La 3-bola con esta identificación del límite es P 3 ( R ). Una situación similar se aplica al aplicar una transformada de Cayley a la matriz antisimétrica.
El ángulo del eje da parámetros en S 2 × S 1 ; si reemplazamos el vector unitario por el eje de rotación real, de modo que n y − n den la misma línea de eje, el conjunto de ejes se convierte en P 2 ( R ), el plano proyectivo real . Pero como las rotaciones alrededor de n y − n están parametrizadas por valores opuestos de θ, el resultado es un fibrado S 1 sobre P 2 ( R ), que resulta ser P 3 ( R ).
Las transformaciones lineales fraccionarias utilizan cuatro parámetros complejos, a , b , c y d , con la condición de que ad − bc sea distinto de cero. Dado que multiplicar los cuatro parámetros por el mismo número complejo no cambia el parámetro, podemos insistir en que ad − bc = 1. Esto sugiere escribir ( a , b , c , d ) como una matriz compleja de 2 × 2 de determinante 1, es decir, como un elemento del grupo lineal especial SL(2, C ). Pero no todas esas matrices producen rotaciones: también se incluyen las funciones conformes en S 2 . Para obtener solo rotaciones insistimos en que d es el conjugado complejo de a , y c es el negativo del conjugado complejo de b . Entonces tenemos dos números complejos, a y b , sujetos a | a | 2 +| b | 2 = 1. Si escribimos a + bj , este es un cuaternión de longitud unitaria.
En última instancia, dado que R 3 no es P 3 ( R ), habrá un problema con cada uno de estos enfoques. En algunos casos, debemos recordar que ciertos valores de parámetros dan como resultado la misma rotación y, para eliminar este problema, se deben establecer límites, pero luego un camino a través de esta región en R 3 debe saltar repentinamente a una región diferente cuando cruza un límite. El bloqueo del cardán es un problema cuando la derivada de la función no es de rango completo, lo que ocurre con los ángulos de Euler y los ángulos de Tait-Bryan, pero no para las otras opciones. La representación del cuaternión no tiene ninguno de estos problemas (es una función dos a uno en todas partes), pero tiene 4 parámetros con una condición (longitud unitaria), lo que a veces hace que sea más difícil ver los tres grados de libertad disponibles.
Un área en la que estas consideraciones, de alguna forma, se vuelven inevitables, es la cinemática de un cuerpo rígido . Se puede tomar como definición la idea de una curva en el grupo euclidiano E (3) del espacio euclidiano tridimensional , comenzando en la identidad (posición inicial). El subgrupo de traslación T de E (3) es un subgrupo normal , con cociente SO(3) si observamos solo el subgrupo E + (3) de isometrías directas (lo cual es razonable en cinemática). La parte traslacional se puede desacoplar de la parte rotacional en la cinemática newtoniana estándar considerando el movimiento del centro de masa y las rotaciones del cuerpo rígido alrededor del centro de masa. Por lo tanto, cualquier movimiento del cuerpo rígido conduce directamente a SO(3), cuando factorizamos la parte traslacional.
Estas identificaciones ilustran que SO(3) está conectado , pero no simplemente conectado . En cuanto a esto último, en la bola con puntos de superficie antípoda identificados, considere la ruta que va desde el "polo norte" directamente a través del centro hasta el polo sur. Este es un bucle cerrado, ya que el polo norte y el polo sur están identificados. Este bucle no se puede encoger a un punto, ya que no importa cómo se deforme el bucle, el punto de inicio y el punto final deben permanecer antípoda, o de lo contrario el bucle se "abrirá". En términos de rotaciones, este bucle representa una secuencia continua de rotaciones sobre el eje z que comienzan y terminan en la rotación identidad (es decir, una serie de rotaciones a través de un ángulo φ donde φ va de 0 a 2π).
Sorprendentemente, si recorremos el camino dos veces, es decir, desde el polo norte hasta el polo sur y de vuelta al polo norte de modo que φ vaya de 0 a 4π, obtenemos un bucle cerrado que puede reducirse a un único punto: primero movemos los caminos de forma continua hasta la superficie de la pelota, conectando aún el polo norte con el polo sur dos veces. La segunda mitad del camino puede entonces reflejarse en el lado antípoda sin cambiar el camino en absoluto. Ahora tenemos un bucle cerrado normal en la superficie de la pelota, que conecta el polo norte consigo mismo a lo largo de un gran círculo. Este círculo puede reducirse al polo norte sin problemas. El truco de la placa balinesa y otros trucos similares lo demuestran de forma práctica.
El mismo argumento se puede realizar en general, y muestra que el grupo fundamental de SO(3) es un grupo cíclico de orden 2. En aplicaciones de física, la no trivialidad del grupo fundamental permite la existencia de objetos conocidos como espinores , y es una herramienta importante en el desarrollo del teorema de estadística de espín .
La cubierta universal de SO(3) es un grupo de Lie llamado Spin(3) . El grupo Spin(3) es isomorfo al grupo unitario especial SU(2); también es difeomorfo a la 3-esfera unitaria S 3 y puede entenderse como el grupo de cuaterniones unitarios (es decir, aquellos con valor absoluto 1). La conexión entre cuaterniones y rotaciones, comúnmente explotada en gráficos de computadora , se explica en cuaterniones y rotaciones espaciales . La función de S 3 sobre SO(3) que identifica puntos antípodas de S 3 es un homomorfismo sobreyectivo de grupos de Lie, con núcleo {±1}. Topológicamente, esta función es una función de cubierta dos a uno .