En geodesia , la figura de la Tierra es el tamaño y la forma que se utilizan para modelar el planeta Tierra . El tipo de figura depende de la aplicación, incluida la precisión necesaria para el modelo. Una Tierra esférica es una aproximación histórica bien conocida que resulta satisfactoria para la geografía , la astronomía y muchos otros propósitos. Se han desarrollado varios modelos con mayor precisión (incluido el elipsoide ) para que los sistemas de coordenadas puedan satisfacer las necesidades precisas de navegación , topografía , catastro , uso de la tierra y varias otras preocupaciones.
La superficie topográfica de la Tierra se manifiesta en su variedad de formas terrestres y zonas de agua. Esta superficie topográfica es, por lo general, objeto de interés para los topógrafos, hidrógrafos y geofísicos . Si bien es la superficie sobre la que se realizan las mediciones de la Tierra, su modelado matemático teniendo en cuenta las irregularidades sería extremadamente complicado.
El concepto pitagórico de una Tierra esférica ofrece una superficie simple que es fácil de manejar matemáticamente. Muchos cálculos astronómicos y de navegación utilizan una esfera para modelar la Tierra como una aproximación cercana. Sin embargo, se necesita una figura más precisa para medir distancias y áreas en la escala más allá de la puramente local. Se pueden hacer mejores aproximaciones modelando toda la superficie como un esferoide achatado , utilizando armónicos esféricos para aproximarse al geoide o modelando una región con un elipsoide de referencia de mejor ajuste .
Para los estudios de áreas pequeñas, es suficiente un modelo plano de la superficie de la Tierra, ya que la topografía local supera la curvatura. Los estudios de planetabla se realizan para áreas relativamente pequeñas sin tener en cuenta el tamaño y la forma de toda la Tierra. Un estudio de una ciudad, por ejemplo, podría realizarse de esta manera.

A finales del siglo XVII, se dedicó un esfuerzo serio a modelar la Tierra como un elipsoide, comenzando con la medición de un grado de arco a lo largo del meridiano de París por parte del astrónomo francés Jean Picard . Los mapas mejorados y la mejor medición de distancias y áreas de territorios nacionales motivaron estos primeros intentos. La instrumentación y las técnicas de topografía mejoraron a lo largo de los siglos siguientes. Los modelos para la figura de la Tierra mejoraron al mismo tiempo.
A mediados y finales del siglo XX, la investigación en el campo de las geociencias contribuyó a mejoras drásticas en la precisión de la figura de la Tierra. La principal utilidad de esta precisión mejorada fue proporcionar datos geográficos y gravitacionales para los sistemas de guía inercial de los misiles balísticos . Esta financiación también impulsó la expansión de las disciplinas geocientíficas, fomentando la creación y el crecimiento de varios departamentos de geociencias en muchas universidades. [1] Estos avances también beneficiaron a muchas actividades civiles, como el control de satélites meteorológicos y de comunicaciones y la localización por GPS , que serían imposibles sin modelos de alta precisión para la figura de la Tierra.
Los modelos para la figura de la Tierra varían en el modo en que se utilizan, en su complejidad y en la precisión con que representan el tamaño y la forma de la Tierra.
.JPG/440px-Horizon,_Valencia_(Spain).JPG)
El modelo más simple para la forma de toda la Tierra es una esfera. El radio de la Tierra es la distancia desde el centro de la Tierra hasta su superficie, aproximadamente 6.371 km (3.959 mi). Si bien el "radio" normalmente es una característica de las esferas perfectas, la Tierra se desvía de la forma esférica en solo un tercio de un porcentaje, lo suficientemente cerca como para tratarla como una esfera en muchos contextos y justificar el término "el radio de la Tierra".
El concepto de una Tierra esférica se remonta a alrededor del siglo VI a. C. , [2] pero siguió siendo un tema de especulación filosófica hasta el siglo III a . C. La primera estimación científica del radio de la Tierra fue dada por Eratóstenes alrededor del 240 a. C., con estimaciones de la precisión de la medición de Eratóstenes que oscilaban entre el -1 % y el 15 %.
La Tierra es aproximadamente esférica, por lo que no existe un valor único que sirva como su radio natural. Las distancias desde los puntos de la superficie hasta el centro varían de 6.353 km (3.948 mi) a 6.384 km (3.967 mi). Varias formas diferentes de modelar la Tierra como una esfera arrojan un radio medio de 6.371 km (3.959 mi). Independientemente del modelo, cualquier radio se encuentra entre el mínimo polar de aproximadamente 6.357 km (3.950 mi) y el máximo ecuatorial de aproximadamente 6.378 km (3.963 mi). La diferencia de 21 km (13 mi) corresponde a que el radio polar es aproximadamente un 0,3 % más corto que el radio ecuatorial.

Como teorizaron Isaac Newton y Christiaan Huygens , [3] : 4 la Tierra es aplanada en los polos y abultada en el ecuador . Por lo tanto, la geodesia representa la figura de la Tierra como un esferoide achatado . El esferoide achatado, o elipsoide achatado , es un elipsoide de revolución obtenido al rotar una elipse sobre su eje más corto. Es la forma geométrica regular que más se aproxima a la forma de la Tierra. Un esferoide que describe la figura de la Tierra u otro cuerpo celeste se llama elipsoide de referencia . El elipsoide de referencia para la Tierra se llama elipsoide de la Tierra .
Un elipsoide de revolución se define de forma única mediante dos magnitudes. En geodesia se utilizan varias convenciones para expresar las dos magnitudes, pero todas son equivalentes y convertibles entre sí:
La excentricidad y el aplanamiento son formas diferentes de expresar cuán aplastado está el elipsoide. Cuando el aplanamiento aparece como una de las cantidades definitorias en geodesia, generalmente se expresa por su recíproco. Por ejemplo, en el esferoide WGS 84 que utilizan los sistemas GPS actuales, el recíproco del aplanamiento se establece exactamente en 298,257 223 563 .
La diferencia entre una esfera y un elipsoide de referencia para la Tierra es pequeña, solo alrededor de una parte en 300. Históricamente, el aplanamiento se calculaba a partir de mediciones de pendiente . Hoy en día, se utilizan redes geodésicas y geodesia por satélite . En la práctica, se han desarrollado muchos elipsoides de referencia a lo largo de los siglos a partir de diferentes estudios. El valor de aplanamiento varía ligeramente de un elipsoide de referencia a otro, lo que refleja las condiciones locales y si el elipsoide de referencia está destinado a modelar toda la Tierra o solo una parte de ella.
Una esfera tiene un único radio de curvatura , que es simplemente el radio de la esfera. Las superficies más complejas tienen radios de curvatura que varían a lo largo de la superficie. El radio de curvatura describe el radio de la esfera que mejor se aproxima a la superficie en ese punto. Los elipsoides achatados tienen un radio de curvatura constante de este a oeste a lo largo de paralelos , si se dibuja una retícula en la superficie, pero una curvatura variable en cualquier otra dirección. Para un elipsoide achatado, el radio de curvatura polar es mayor que el ecuatorial.
porque el polo es aplanado: cuanto más plana sea la superficie, más grande debe ser la esfera para aproximarse a ella. Por el contrario, el radio de curvatura norte-sur del elipsoide en el ecuador es menor que el del polo.
donde es la distancia del centro del elipsoide al ecuador (semieje mayor), y es la distancia del centro al polo. (semieje menor)
La posibilidad de que el ecuador de la Tierra se caracterice mejor como una elipse en lugar de un círculo y, por lo tanto, que el elipsoide sea triaxial, ha sido un tema de investigación científica durante muchos años. [4] [5] Los avances tecnológicos modernos han proporcionado métodos nuevos y rápidos para la recopilación de datos y, desde el lanzamiento del Sputnik 1 , se han utilizado datos orbitales para investigar la teoría de la elipticidad. [3] Los resultados más recientes indican una diferencia de 70 m entre los dos ejes ecuatoriales de inercia mayor y menor, con el semidiámetro más grande apuntando a 15° de longitud oeste (y también a 180 grados de distancia). [6] [7]
Siguiendo el trabajo de Picard, el erudito italiano Giovanni Domenico Cassini descubrió que la longitud de un grado era aparentemente más corta al norte de París que al sur, lo que implicaba que la Tierra tenía forma de huevo . [3] : 4 En 1498, Cristóbal Colón sugirió dudosamente que la Tierra tenía forma de pera basándose en sus dispares lecturas móviles del ángulo de la Estrella del Norte , que interpretó incorrectamente como de movimiento diurno variable . [8]
La teoría de una Tierra ligeramente en forma de pera surgió cuando se recibieron datos del satélite artificial estadounidense Vanguard 1 en 1958. Se descubrió que variaba en su órbita periódica larga, y que el hemisferio sur exhibía una atracción gravitatoria mayor que el hemisferio norte. Esto indicó un aplanamiento en el Polo Sur y un abultamiento del mismo grado en el Polo Norte , con un aumento del nivel del mar de unos 9 m (30 pies) en este último. [9] [10] [3] : 9 Esta teoría implica que las latitudes medias del norte están ligeramente aplanadas y las latitudes medias del sur están abultadas correspondientemente. [3] : 9 Los factores potenciales involucrados en esta aberración incluyen las mareas y el movimiento subcortical (por ejemplo, la tectónica de placas ). [9] [10]
A John A. O'Keefe y sus coautores se les atribuye el descubrimiento de que la Tierra tenía un armónico esférico zonal de tercer grado significativo en su campo gravitatorio utilizando datos del satélite Vanguard 1. [11] Basándose en más datos de geodesia satelital , Desmond King-Hele refinó la estimación a una diferencia de 45 m (148 pies) entre los radios polares norte y sur, debido a un "tallo" de 19 m (62 pies) que se eleva en el Polo Norte y una depresión de 26 m (85 pies) en el Polo Sur. [12] [13] La asimetría polar es aproximadamente mil veces más pequeña que el aplanamiento de la Tierra e incluso más pequeña que su ondulación geoidal en algunas regiones. [14]

La geodesia moderna tiende a conservar el elipsoide de revolución como elipsoide de referencia y a tratar la triaxialidad y la forma de pera como parte de la figura del geoide : están representadas por los coeficientes armónicos esféricos y , respectivamente, correspondientes a los números de grado y orden 2,2 para la triaxialidad y 3,0 para la forma de pera.
Se ha dicho antes que las mediciones se realizan en la superficie aparente o topográfica de la Tierra y se acaba de explicar que los cálculos se realizan en un elipsoide. Hay otra superficie que interviene en la medición geodésica: el geoide. En la topografía geodésica, el cálculo de las coordenadas geodésicas de los puntos se realiza habitualmente en un elipsoide de referencia que se aproxima mucho al tamaño y la forma de la Tierra en el área de la topografía. Sin embargo, las mediciones reales realizadas en la superficie de la Tierra con ciertos instrumentos se refieren al geoide. El elipsoide es una superficie regular definida matemáticamente con dimensiones específicas. El geoide, por otro lado, coincide con la superficie a la que se conformarían los océanos en toda la Tierra si tuvieran libertad para ajustarse al efecto combinado de la atracción de la masa de la Tierra ( gravitación ) y la fuerza centrífuga de la rotación de la Tierra . Como resultado de la distribución desigual de la masa de la Tierra, la superficie geoidal es irregular y, dado que el elipsoide es una superficie regular, las separaciones entre ambos, denominadas ondulaciones geoidales , alturas geoidales o separaciones geoidales, también serán irregulares.
El geoide es una superficie a lo largo de la cual el potencial de gravedad es igual en todas partes y a la cual la dirección de la gravedad es siempre perpendicular. Esto último es particularmente importante porque los instrumentos ópticos que contienen dispositivos de nivelación de referencia de gravedad se utilizan comúnmente para realizar mediciones geodésicas. Cuando se ajusta correctamente, el eje vertical del instrumento coincide con la dirección de la gravedad y, por lo tanto, es perpendicular al geoide. El ángulo entre la plomada que es perpendicular al geoide (a veces llamada "la vertical") y la perpendicular al elipsoide (a veces llamada "la normal elipsoidal") se define como la desviación de la vertical . Tiene dos componentes: un componente este-oeste y un componente norte-sur. [3]
Son posibles aproximaciones locales más simples.
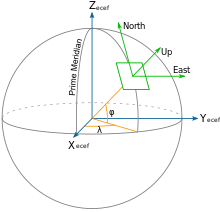
El plano tangente local es apropiado para el análisis en distancias pequeñas.

La mejor aproximación esférica local al elipsoide en la proximidad de un punto dado es la esfera osculadora de la Tierra . Su radio es igual al radio de curvatura gaussiano de la Tierra y su dirección radial coincide con la dirección normal geodésica . El centro de la esfera osculadora está desplazado del centro del elipsoide, pero está en el centro de curvatura para el punto dado en la superficie del elipsoide. Este concepto ayuda a la interpretación de las mediciones de refracción de ocultación de radio terrestres y planetarias y en algunas aplicaciones de navegación y vigilancia. [15] [16]
La determinación de la forma exacta de la Tierra no es sólo una tarea geométrica de la geodesia, sino que también tiene consideraciones geofísicas . Según los argumentos teóricos de Newton, Leonhard Euler y otros, un cuerpo que tenga una densidad uniforme de 5.515 kg/m 3 y que gire como la Tierra debería tener un aplanamiento de 1:229. Esto se puede concluir sin ninguna información sobre la composición del interior de la Tierra . [17] Sin embargo, el aplanamiento medido es de 1:298,25, que está más cerca de una esfera y es un argumento sólido de que el núcleo de la Tierra es extremadamente compacto. Por lo tanto, la densidad debe ser una función de la profundidad, que va desde 2.600 kg/m 3 en la superficie (densidad de la roca del granito , etc.), hasta 13.000 kg/m 3 dentro del núcleo interno. [18]
También tiene implicaciones para la exploración física del interior de la Tierra el campo gravitatorio , que es el efecto neto de la gravitación (debida a la atracción de masas) y la fuerza centrífuga (debida a la rotación). Se puede medir con mucha precisión en la superficie y de forma remota mediante satélites. La vertical verdadera generalmente no corresponde a la vertical teórica ( la desviación varía hasta 50") porque la topografía y todas las masas geológicas perturban el campo gravitatorio. Por lo tanto, la estructura bruta de la corteza y el manto de la Tierra se puede determinar mediante modelos geodésicos-geofísicos del subsuelo.
![]() Este artículo incorpora texto de esta fuente, que se encuentra en el dominio público : Defense Mapping Agency (1983). Geodesia para el profano (informe). Fuerza Aérea de los Estados Unidos.
Este artículo incorpora texto de esta fuente, que se encuentra en el dominio público : Defense Mapping Agency (1983). Geodesia para el profano (informe). Fuerza Aérea de los Estados Unidos.