Topología cociente
En matemáticas, la topología cociente consiste intuitivamente en crear una topología pegando ciertos puntos sobre otros, en un espacio dado, por medio de una relación de equivalencia bien definida.
El nuevo espacio así generado recibe el nombre de espacio cociente.
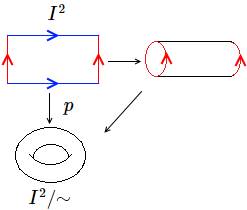
Ejemplos conocidos son el toro matemático o la banda de Möbius.
un espacio topológico y
: Los conjuntos abiertos que conforman la llamada topología cociente sobre
son los conjuntos de las clases de equivalencia cuyas uniones son conjuntos abiertos en
: Definición equivalente: sea la aplicación proyección
, se definen los abiertos de
Es decir, un conjunto de clases de equivalencia es abierto si los elementos que las forman son un conjunto abierto de la topología original.
por definición de topología cociente.
{\displaystyle p^{-1}(U_{i})\in {\mathcal {T}}_{X}\quad \forall i=1,\dots ,n}
por definición de topología cociente.
{\displaystyle \bigcap _{i=1}^{n}{p^{-1}(U_{i})}\in {\mathcal {T}}_{X}}
más fina que
, por definición, necesariamente tiene un abierto
, y esto contradice la definición de continuidad.
abierto y veamos que su antiimagen por
Esto es equivalente, por definición de topología cociente, a ver que
En los siguientes ejemplos los homeomorfismos se construyen primero deformando el espacio cociente sin tener en cuenta la relación de equivalencia (cortándola) y después pegando los trozos que estaban relacionados.
Es decir, estamos admitiendo que podemos construir un homeomorfismo entre dos espacios cociente a partir de uno entre los espacios originales siempre y cuando los elementos relacionados antes y después del homeomorfismo sean los mismos.
Este resultado, que justifica que las construcciones siguientes son correctas, se conoce como lema de cortar y pegar, y se demuestra a continuación Entonces, la aplicación
está bien definida y es un homeomorfismo.
es homeomorfismo y, en particular, exhaustiva,
f ( x ) = y
es inyectiva: Supongamos que
y veamos que
es continua por ser homeomorfismo y
por ser una proyección al cociente.
, pero por la segunda propiedad del apartado de propiedades esto quiere decir que
La demostración es la misma que