Sistema de referencia no inercial

En mecánica newtoniana, un sistema de referencia no inercial es un sistema de referencia en el que no se cumplen las leyes del movimiento de Newton cuando sólo se consideran las fuerzas reales (no ficticias).Dado un sistema de referencia inercial, un segundo sistema de referencia será no inercial cuando describa un movimiento acelerado con respecto al primero.La aceleración del sistema no inercial puede deberse a: Un ejemplo de sistema no inercial podría ser el correspondiente a un sistema de coordenadas "fijo en la Tierra", en el cual los movimientos de los cuerpos serían medidos respecto a puntos de la Tierra que estarían girando.Un observador situado en un sistema de referencia no inercial deberá recurrir a fuerzas ficticias (tales como la fuerza de Coriolis o la fuerza centrífuga) para poder explicar los movimientos con respecto a dicho sistema de referencia.Estas fuerzas no existen realmente, en el sentido de que no son causadas directamente por la interacción con otro objeto, pero deberán introducirse si se quiere explicar el fenómeno según las leyes de Newton.Siendo rigurosos podría argumentarse que los sistemas de referencia inerciales no existen, o al menos no en nuestro entorno, pues la Tierra gira sobre sí misma y también alrededor del Sol, y este a su vez lo hace respecto al centro de la Vía Láctea.Consideremos una plataforma giratoria dando vueltas con una velocidad angularUn observador situado en el sistema de referencia no inercial (O', x', y', z') percibe que los objetos tienden a dirigirse hacia el exterior de la plataforma, con dirección radial.Comprueba la tensión que adquiere la cuerda (T en la figura 2), y la justifica con la existencia de una fuerza con el mismo módulo que la tensión pero con dirección contraria, como la representada porSin embargo, para un observador situado en el sistema de referencia (O, x, y, z) la única fuerza que interviene en el movimiento del objeto situado sobre la plataforma es la tensión de la cuerda (supongamos que no existe rozamiento con la plataforma).Así, únicamente el observador situado en el sistema de referencia no inercial necesitará fuerzas ficticias para explicar el movimiento.) respecto a un sistema de referencia inercial (figura 3).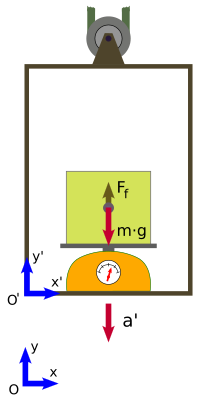Un observador situado en el interior del ascensor y sin referencias exteriores cree estar en un sistema inercial dentro del campo gravitatorio terrestre.y estudia el movimiento respecto a un sistema de referencia situado en el suelo del ascensor.Por tanto, la expresión para obtener el tiempo correcto sería: Sin embargo, un observador situado en el sistema de referencia inercial no tendrá que recurrir a ninguna fuerza ficticia para explicar el movimiento.También podríamos observar una violación de las leyes de Newton, si situáramos una masa conocida en una báscula fijada al suelo del ascensor.Es decir: Razonamientos similares pueden realizarse para el caso en el que el ascensor estuviera ascendiendo con una aceleraciónLa diferencia está en que la fuerza ficticia tendría dirección contraria (estaría dirigida hacia abajo).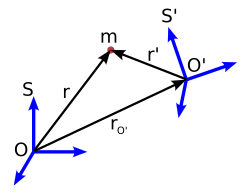Consideremos que S sea un sistema fijo y que S' sea un sistema de referencia no inercial con movimiento acelerado respecto al primero (translación y/o rotación).Se puede demostrar[1]​[2]​ que las derivadas temporales de un vector cualquieraSea un objeto de masa m, situado respecto a los sistemas de referencia S y S', según se muestra en la figura 6.Derivando la ecuación (2) respecto al tiempo y aplicando (1), obtenemos: (3)Volviendo a derivar y aplicando de nuevo la ecuación (1), obtenemos la expresión:con lo que la aceleración del objeto en el sistema de referencia no inercial será: (5)Y multiplicando por la masa se obtiene finalmente la segunda ley de Newton para el sistema de referencia no inercial: (6)Comparando las ecuaciones (6) y (7) se observa que para el caso del sistema referencia no inercial han aparecido cuatro términos, conocidos como fuerzas ficticias por no deberse a la interacción del objeto con otros cuerpos: 1: es una fuerza que solo estará presente en los sistemas con aceleración angular 4: es debida a la aceleración del origen de S' respecto a S. Los cuatro términos aparecen con signo negativo, y corresponden a aceleraciones sufridas por el sistema S', con centro en O', respecto al sistema inercial S, con centro en O, y cada uno de ellos compensa una forma de aceleración sufrida por el sistema S' respecto a S. Esto es, las fuerzas ficticias son la compensación de las fuerzas necesarias para que el sistema S' este acelerado respecto a S. La mecánica relativista considera sistemas mecánicos moviéndose en un espacio-tiempo plano o espacio de Minkowski.En dicha teoría cualquier sistema de coordenadas admisible es válido para representar el movimiento., donde: En un sistema de referencia inercial relativista, dado que