Ecuación de Arrhenius
La ecuación de Arrhenius es una expresión matemática que se utiliza para comprobar la dependencia de la constante de velocidad (o cinética) de una reacción química con respecto a la temperatura a la que se lleva a cabo esa reacción.
[1] La ecuación fue propuesta primeramente por el químico neerlandés J. H. van 't Hoff en 1884; cinco años después en 1889 el químico sueco Svante Arrhenius dio una justificación física y una interpretación para la ecuación.
Actualmente, es vista mejor como una relación empírica.
de reacciones químicas a la temperatura
(en temperatura absoluta, tales como kelvins o grados Rankine) y la energía de activación[3]
Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.
Cuando se grafica de la forma descrita anteriormente, el valor de la intersección en el eje y corresponderá a
, y la pendiente de la línea será igual a
representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.
: Arrhenius argumentó que para que los reactivos se transformen en productos, deben primero adquirir una mínima cantidad de energía, llamada la "energía de activación" Ea.
A una cierta temperatura absoluta T, la fracción de las moléculas que tiene una energía cinética mayor que Ea puede ser calculada a partir de la distribución de Maxwell-Boltzmann de la mecánica estadística, y resulta ser proporcional a
En esta teoría, se supone que las moléculas reaccionan si colisionan con una energía cinética relativa a lo largo de sus líneas de centro, que exceda Ea.
Esto toma varias formas, pero una de las más comunes es: A primera vista, esto luce como un exponencial multiplicado por un factor que es lineal en temperatura.
Sin embargo, se debe recordar que la energía libre es por sí misma una cantidad dependiente de la temperatura.
Cuando todos los detalles son considerados, se termina con una expresión que nuevamente toma la forma de la ecuación exponencial de Arrhenius multiplicada por una función de
) son determinadas experimentalmente, y representan parámetros macroscópicos específicos de la reacción que no están relacionados de manera simple a las energías umbrales y al éxito de las colisiones individuales a nivel molecular.
Considérese una colisión particular (una reacción elemental) entre las moléculas A y B.
El ángulo de colisión, la energía traslacional relativa, la energía (particularmente la vibracional) interna, todos esos factores determinarán la oportunidad de que la colisión produzca una molécula AB.
Para probar las velocidades de reacción a nivel molecular, los experimentos tienen que ser realizados bajo condiciones casi colisionales y este tópico es llamado en ocasiones dinámica de reacciones moleculares.
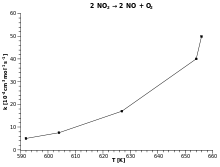
k respecto a T

ln(k) respecto a 1/T