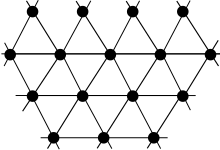
Gráfico de celosía

Este gráfico es todo aquel cuyo dibujo, incrustado en algún espacio euclídeo R n, forma un mosaico regular.

Esto implica que el grupo de transformaciones biyectivas que envía el gráfico a sí mismo es una celosía en el sentido teórico de grupo.

Normalmente, no se hace una distinción clara entre un gráfico de este tipo en el sentido más abstracto de la teoría de grafos y su dibujo en el espacio (a menudo el plano o el espacio 3D).

Este tipo de gráfico se puede llamar más brevemente simplemente una celosía, malla o cuadrícula.

Además, estos términos también se usan comúnmente para una sección finita del gráfico infinito, como en "una cuadrícula cuadrada de 8 × 8".

[1]​ Un tipo común de gráfico de celosía (conocido con diferentes nombres, como gráfico de cuadrícula cuadrada) es el gráfico cuyos vértices corresponden a los puntos en el plano con coordenadas enteras, las coordenadas x están en el rango 1, ..., n, Las coordenadas y están en el rango 1, ..., my dos vértices están conectados por un borde siempre que los puntos correspondientes están a la distancia 1.