Teorema de Bell
En cada intento, cada observador independientemente elige entre varios ajustes del detector y realiza una medida sobre la partícula (Nota: aunque la propiedad entrelazada utilizada aquí es el espín de la partícula, podría haber sido cualquier "estado cuántico" entrelazado que codifique exactamente un bit cuántico.)
De hecho, los resultados pueden explicarse añadiendo variables ocultas locales - cada par de partículas podría haberse enviado con instrucciones sobre cómo comportarse según se las mida en los dos ejes (si '+' o '−' para cada eje).
Pero (si se generan por igual todos las posibles combinaciones de + y −) cuando ellos midan sobre ejes perpendiculares verán correlación cero.
El teorema de Bell muestra que si las partículas se comportan como predice la mecánica cuántica, Alicia y Bob pueden puntuar más alto que la predicción clásica de variables ocultas de correlación +0.5; si los aparatos se rotan 45° entre sí, la mecánica cuántica predice que la puntuación esperada promedio será 0.71.
Todavía existen científicos que no están de acuerdo con estos hallazgos [3].
El teorema de Bell parece poner punto final a las esperanzas del realismo local para la MC.
Se necesitan experimentos para determinar cuál es correcto, pero llevó muchos años y muchos avances en la tecnología el poder realizarlos.
Estos resultados proveen evidencia empírica contra el realismo local y en favor de la MC.
En el experimento de Bell, Alicia puede elegir el ajuste del detector para medir o bien
Lo mismo es cierto si ambos espines son medidos en las direcciones B o C. Es seguro concluir que cualquier variable oculta que determinase las medidas de A, B y C en las dos partículas está correlacionada al 100% y puede utilizarse indistintamente en ambas.
Pero si A se mide en una partícula y C en la otra, los resultados están correlacionados solo en un 96%, lo que es una contradicción.
Adicionalmente a la desigualdad de Bell original,[2] la forma dada por John Clauser, Michael Horne, Abner Shimony and R. A. Holt,[3] (the CHSH form) es especialmente importante,[3] porque da límites clásicos a la correlación esperada para el experimiento anterior realizado por Alicia y Bob: donde C denota correlación.
Es fácil ver que esto es cierto en el caso más general: Para justificar el límite superior 2 afirmado en la última inecuación, sin pérdida de generalidad, podemos asumir que En ese caso Nota 2.
Fue entonces restringido (en muchos trabajos teóricos) a significar solo aquellos componentes que estuvieran asociados con la fuente.
Sin embargo, con la extensión probada en la Nota 1, la desigualdad de CHSH todavía se cumple incluso si los propios instrumentos contienen ellos mismos variables ocultas.
Ahora apliquemos el formalismo CHSH a las medidas que pueden ser realizadas por Alicia y Bob.
Los operadores que dan este valor máximo son siempre isomorfos a las matrices de Pauli.
Los tests experimentales pueden determinar si las desigualdades de Bell requeridas por el realismo local se mantienen bajo evidencia empírica.
[5] De los trece experimentos listados, solo dos alcanzaron resultados contradictorios con la mecánica cuántica; además, de acuerdo a la misma fuente, cuando se repitieron los experimentos, "las discrepancias con la MC no pudieron ser reproducidas".
Debemos recordar las palabras cautelosas de Albert Einstein[7] poco antes de morir: "Hoy en día cada Tom, Dick y Harry ('jeder Kerl' en el alemán original) piensa que sabe lo que es un fotón, pero está equivocado".
Se sigue que no todas las señales tienen la misma probabilidad de detección (Marshall y Santos 2002[5]).
Por ello, teniendo en cuenta esta baja eficiencia del detector, la predicción MC realmente cumplía la DBI.
Para llegar al diseño experimental donde la predicción de la MC viola la DBI necesitamos detectores cuya eficiencia exceda del 82% para estados singlete, pero tenemos tasas oscuras muy bajas y tiempos muertos y de resolución muy bajos.
2006[6]) por lo que el optimismo de Shimony en la Stanford Encyclopedia, mencionado en la sección precedente, parece exagerado.
Entonces, si se interpone un polarizador entre la cascada y el detector, la probabilidad de detección no puede aumentar.
Esto es quizá no sorprendente, puesto que es sabido que añadir ruido a los datos puede, en presencia de un umbral, ayudar a revelar señales ocultas (esta propiedad es conocida como resonancia estocástica [7]).
En esta controvertida aproximación, dos observadores distantes se dividen en superposiciones al medir un espín.
Las violaciones de las desigualdades de Bell ya no son contraintuitivas, pues no está claro qué copia del observador B verá a qué copia del observador A cuando comparen las medidas.
Esta establece que si el resultado de un experimento se observa siempre de forma definida, existe una cantidad que determina cuál hubiera sido la salida aunque no se realice el experimento.
Esta extraña no localidad fue originalmente un supuesto argumento de reductio ad absurdum, porque la interpretación estándar podría fácilmente eliminar la acción a distancia simplemente asignando a cada partícula estados de espín definidos.
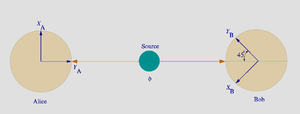

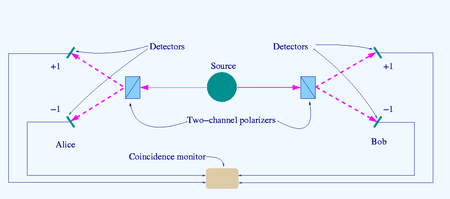
La fuente SOURCE produce pares de "fotones", enviados en direcciones opuestas. Cada fotón encuentra un polarizador de dos canales cuya orientación (a o b) pueda ser ajustada por el experimentador. Las señales emergentes de cada canal son detectadas y las coincidencias de cuatro tipos (++, −−, +− y −+) son contadas por el monitor de coincidencias.