Sección cónica

En matemática, y concretamente en geometría, se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono recto y un plano;[1]​ si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas elipse, parábola, hipérbola y circunferencia.Las secciones cónicas en el plano euclídeo tienen varias propiedades distintivas, muchas de las cuales pueden utilizarse como definiciones alternativas.Una de estas propiedades define una cónica no circular[2]​ como el conjunto de aquellos puntos cuyas distancias a algún punto en particular, llamado foco, y a alguna línea en particular, llamada directriz, están en una proporción fija, llamada excentricidad'.En el plano euclídeo, los tres tipos de secciones cónicas parecen bastante diferentes, pero comparten muchas propiedades.Al extender el plano euclídeo para incluir una recta en el infinito, obteniendo un plano proyectivo, la diferencia aparente desaparece: las ramas de una hipérbola se encuentran en dos puntos en el infinito, lo que la convierte en una única curva cerrada; y los dos extremos de una parábola se encuentran para convertirla en una curva cerrada tangente a la recta en el infinito.La primera definición conocida de sección cónica surge en la Antigua Grecia, cerca del año 340 a. 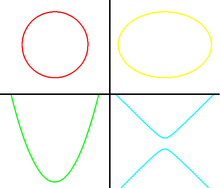C., (Menecmo) donde fueron definidas como secciones «de un cono circular recto».Las secciones cónicas se han estudiado durante miles de años y han proporcionado una rica fuente de resultados interesantes y bellos en geometría euclidiana.Hay tres tipos de cónicas: la elipse, la parábola y la hipérbola.Las elipses surgen cuando la intersección del cono y el plano es una curva cerrada.Si el plano de corte es paralelo a exactamente una recta generatriz del cono, entonces la cónica es no acotada y se denomina parábola.En el caso restante, la figura es una hipérbola: el plano interseca ambas mitades del cono, produciendo dos curvas separadas no acotadas.La excentricidad de una circunferencia se define como cero y su foco es el centro de la circunferencia, pero su directriz sólo puede tomarse como la recta al infinito en el plano proyectivo.[4]​.Una parábola también puede definirse en términos de su foco y su recta latus (paralela a la directriz y que pasa por el foco): es el lugar geométrico de los puntos cuya distancia al foco más o menos la distancia a la recta es igual a 2a; más si el punto está entre la directriz y la recta latus, menos en caso contrario.En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber: Si el plano pasa por el vértice del cono, se puede comprobar que: Se denomina ecuación general de segundo grado o ecuación cuadrática general en dos variablesdonde a, h, b, g, f, c son constantes reales, y al menos uno de los valores a, b, h es no nulo.La elipse, parábola, hipérbola son curvas de segundo grado por satisfacer ecuaciones de la forma (1), pero hay curvas de segundo grado que no son secciones cónicas, para el caso: dan un punto, una recta, dos rectas, ningún punto.A continuación se presentan los tres casos: parábola, elipse e hipérbola.La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante positiva.La elipse posee la ecuación ordinaria (con centro en el origen de coordenadas):La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante y menor que la distancia entre los focos.Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo.También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.[9]​[10]​ Su trabajo no sobrevivió, ni siquiera los nombres que utilizó para estas curvas, y solo se conoce a través de relatos secundarios.Se determinaban tres tipos de conos por sus ángulos de vértice (medidos por el doble del ángulo formado por la hipotenusa y el cateto sobre el que se giraba el triángulo rectángulo).[12]​ Se dice que Euclides (hacia el año 300 a. C.) escribió cuatro libros sobre cónicas, pero también se perdieron[28] Se sabe que Arquímedes (fallecido hacia el año 212 a. C.) estudió las cónicas, habiendo determinado el área limitada por una parábola y una cuerda en Cuadratura de la Parábola.Apolonio utilizó los nombres de «elipse», «parábola» e «hipérbola» para estas curvas, tomando prestada la terminología de los trabajos pitagóricos anteriores sobre áreas.[16]​ El matemático islámico Abū Sahl al-Qūhī describió por primera vez en el año 1000 un instrumento para dibujar secciones cónicas.Los persas encontraron aplicaciones de la teoría, sobre todo el matemático y poeta persa Omar Jayam,[19]​ que encontró un método geométrico para resolver ecuaciones cúbicas utilizando secciones cónicas.En particular, Pascal descubrió un teorema conocido como el hexagrammum mysticum del que se pueden deducir muchas otras propiedades de las cónicas.René Descartes y Pierre Fermat aplicaron su recién descubierta geometría analítica al estudio de las cónicas.