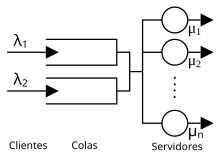
Teoría de colas
Esta teoría estudia factores como el tiempo de espera medio en las colas o la capacidad de trabajo del sistema sin que llegue a colapsar.
Se trata así de una teoría que encuentra aplicación en una amplia variedad de situaciones como negocios, comercio, industria, ingenierías, transporte y logística o telecomunicaciones.
Así, por ejemplo, los procesos enviados a un servidor en red forman colas de espera mientras no son atendidos; la información solicitada a un servidor Web a través de Internet puede recibirse con demora debido a la congestión en la red o en el servidor; en el caso de telefonía (fija o móvil), una llamada puede no ser realizada si alguna central está saturada (un mensaje típico en este caso es "por sobrecarga en red rogamos vuelva a llamar pasados unos minutos").
Estos clientes entran al sistema y se unen a la cola de espera.
Terminado el servicio, el cliente sale del sistema de colas.
En general, la cola de espera se forma (y crece) si durante un tiempo la demanda del servicio es mayor que la capacidad del sistema para suministrarlo.
Los clientes puede que esperen, aunque las instalaciones de servicio sean adecuadas, porque los clientes llegados anteriormente están siendo atendidos (como en el caso mencionado anteriormente).
Por ejemplo, si un usuario necesita un minuto para ser atendido pero los clientes llegan a una tasa mayor de un cliente por minuto, la cola crecerá indefinidamente.
En general, si un cliente llega al sistema y todos los recursos están ocupados, esperará en una cola, salvo que dicha cola esté llena y entonces será rechazado (es decir: no es admitido).
Se pueden identificar los siguientes elementos: David G. Kendall introdujo una notación de colas A/S/c en 1953[2] en la que A describe la distribución del tiempo entre llegada, S la distribución del tiempo de servicio y c el número de recursos disponibles.
Si es finito, el número máximo de clientes permitidos en el sistema está acotado, por lo que nuevas llegadas son rechazadas.
Si el tamaño de la población N es finito, esto supone que cuantos más usuarios se encuentren en el sistema, menos usuarios estarán generando peticiones.
(esto es, teniendo en cuenta únicamente los usuarios que son atendidos, y no los que son rechazados), la relación viene dada por Existe una "demostración gráfica"[6] del teorema, donde resulta destacable las pocas hipótesis de modelado necesarias (esto es: no es necesario suponer llegadas de Poisson, tiempos de servicio exponenciales, etc.).
siguen una distribución de Poisson, sólo hay un servidor y la capacidad del sistema es ilimitada.
En este caso, el número medio de usuarios en el sistema se puede obtener analizando el proceso de nacimiento y muerte resultante, y viene dado por:
Mientras que el número medio de usuarios en la cola viene dado por la expresión:
En este modelo, al igual que en caso anterior, la tasa de llegadas
siguen una distribución de Poisson, y hay un espacio infinito para esperar.
Sin embargo, ahora existen c (un número entero positivo) servidores idénticos en paralelo, y cualquiera de ellos puede atender las peticiones en cuando estén disponibles.
Y al igual que en el caso del M/M/1, únicamente puede analizarse el sistema si
, y que vendría a representar el número mínimo de servidores necesarios para atender la carga en el sistema.
siguen una distribución de Poisson, y existen c servidores idénticos en paralelo.
Dado que no hay cola de espera, cuando un usuario llega al sistema sólo caben dos opciones: si queda algún servidor disponible el usuario es inmediatamente atendido, mientras que si todos los c servidores están ocupado el usuario es rechazado.
Dicha probabilidad es la variable de rendimiento más importante y su expresión se conoce como Erlang-B:
Por ejemplo; los modelos matemáticos a menudo asumen el número de clientes, o la capacidad de la cola infinitos, cuando es evidente que deben estar limitados.
Las redes telefónicas se diseñan para acomodar la intensidad ofrecida del tráfico con solamente una pequeña pérdida.
Esto significa que si los niveles de la intensidad del tráfico exceden de la capacidad disponible, las llamadas del cliente se perderían.
Define la manera en que les servirán, la orden de las cuales se sirven, y la manera en la que los recursos se dividen entre los clientes.
En particular, el supuesto de tiempos entre llegadas exponenciales implica que las llegadas ocurren al azar (proceso de entrada de Poisson), lo cual es una aproximación razonable en muchas situaciones pero no cuando las llegadas están programadas o reguladas con todo cuidado.
Sin embargo, se han podido obtener algunos resultados útiles con algunos modelos.