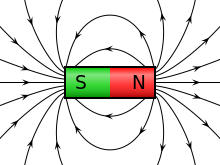
Gráficamente, se suelen representar mediante líneas o superficies de igual magnitud.Esta nueva propuesta se deslindaría formalmente de la física aristotélica.En Aristóteles el espacio (y parecidamente el tiempo) tendía a convertirse en "espacio-de-cada-cosa", es decir, en lugar (ocupado por la cosa).Sin embargo, para Newton, que es decir: a partir de la física clásica, el espacio toma estado de absoluto, o ab-solutum, es decir, desligado (ab) y suelto (solutum) de causas finales y eficientes, y expuesto a fuerzas.Al observar el movimiento de muchos cuerpos que interactúan entre sí, como los planetas en el Sistema Solar, lidiar con la fuerza entre cada par de cuerpos por separado se convierte rápidamente en un inconveniente computacional.En el siglo XVIII, se ideó una nueva cantidad para simplificar la contabilidad de todas estas fuerzas gravitatorias.[3] La naturaleza independiente del campo se hizo más evidente con el descubrimiento de James Clerk Maxwell de que las ondas en estos campos se propagaban a una velocidad finita.Al eliminar la necesidad de un medio de fondo, este desarrollo abrió el camino para que los físicos comenzaran a pensar en los campos como entidades verdaderamente independientes.En 1927, Paul Dirac usó el campo cuántico para explicar con éxito cómo la descomposición de un átomo a un estado cuántico más bajo condujo a la emisión espontánea de un fotón, el cuanto del campo electromagnético.Se dice que existe un campo asociado a una magnitud física, en una región del espacio, si se puede asignar un valor a dicha magnitud para todos los puntos de dicha región en cada instante.En contraste con la física aristotélica, la noción de campo nos permite reconocer a la potencia como algo real.La acción a distancia se explica, entonces, mediante efectos provocados por la entidad causante de la interacción, sobre el espacio mismo que la rodea, permitiendo asignar a dicho espacio propiedades medibles.Los campos más conocidos en física clásica son: Estos dos ejemplos anteriores son los casos de campos de fuerza elementales en física clásica.Matemáticamente si el sistema queda descrito por una serie de coordenadasTodos esos campos se relacionan mediante un sistema complejo de ecuaciones diferenciales en derivadas parciales, generalmente no lineales.
Representación gráfica de un campo magnético mediante
líneas de fuerza
equipotenciales
