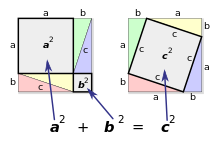
Belleza matemática

A veces son descritas como una forma de arte, o por lo menos, como una actividad creativa.

[4]​ Solamente Carl Friedrich Gauss publicó ocho demostraciones diferentes de este teorema.

[6]​ Otras dos singularidades geométricas aceptadas como de gran belleza desde la antigüedad, son los sólidos platónicos y la Flor de la Vida, que están íntimamente relacionados entre sí y con la proporción áurea.

[8]​ Johannes Kepler dijo al respecto que podía ser considerada «una preciosa joya».

Aunque es muy difícil tener un acuerdo universal entre qué resultados son profundos, algunos ejemplos pueden ser citados.

Un teorema trivial puede ser un resultado que derive en una manera obvia y sencilla a partir de otros resultados conocidos, o que se aplica solo a un conjunto particular de objetos.

Sin embargo, en ocasiones, el establecimiento de un teorema puede ser tan original que puede ser considerado como profundo, aunque su demostración sea obvia.

Cuando Erdos quería expresar una particular apreciación a una demostración, solía exclamar: «¡Ésta es del libro!».

Alain Badiou, filósofo del siglo veinte, dice que la ontología es matemáticas.