Modelo de quarks

Esquema de clasificación de los hadrones

Figura 1 : El nonnet de mesones pseudoescalares . Los miembros del "octeto" de mesones original se muestran en verde, el singlete en magenta. Aunque estos mesones ahora están agrupados en un nonnet, el nombre de Camino Óctuple deriva de los patrones de ocho para los mesones y bariones en el esquema de clasificación original.

En física de partículas , el modelo de quarks es un esquema de clasificación de los hadrones en términos de sus quarks de valencia (los quarks y antiquarks que dan lugar a los números cuánticos de los hadrones). El modelo de quarks es la base del "sabor SU(3)" , o el Camino Óctuple , el exitoso esquema de clasificación que organizó la gran cantidad de hadrones más ligeros que se descubrieron a partir de la década de 1950 y durante la de 1960. Recibió verificación experimental a partir de finales de la década de 1960 y es una clasificación válida y efectiva de ellos hasta la fecha. El modelo fue propuesto de forma independiente por los físicos Murray Gell-Mann ^[1] , quien los denominó "quarks" en un artículo conciso, y George Zweig ^[2] [ ^3], quien sugirió "ases" en un manuscrito más largo. André Petermann también abordó las ideas centrales de 1963 a 1965, sin tanta fundamentación cuantitativa. ^{[4] [5]} Hoy en día, el modelo ha sido absorbido esencialmente como un componente de la teoría cuántica de campos establecida de interacciones de partículas fuertes y electrodébiles, denominada Modelo Estándar .

Los hadrones no son realmente "elementales", y pueden considerarse como estados ligados de sus "quarks de valencia" y antiquarks, que dan lugar a los números cuánticos de los hadrones. Estos números cuánticos son etiquetas que identifican a los hadrones y son de dos tipos. Un conjunto proviene de la simetría de Poincaré : J ^PC , donde J , P y C representan el momento angular total , la simetría P y la simetría C , respectivamente.

El otro conjunto son los números cuánticos de sabor, como el isospín , la extrañeza , el encanto , etc. Las interacciones fuertes que unen a los quarks son insensibles a estos números cuánticos, por lo que la variación de ellos conduce a relaciones sistemáticas de masa y acoplamiento entre los hadrones en el mismo multiplete de sabor.

A todos los quarks se les asigna un número bariónico de ⁠1/3Los quarks up , charm y top tienen una carga eléctrica de +2/3⁠ , mientras que los quarks down , strange y bottom tienen una carga eléctrica de − ⁠1/3Los antiquarks tienen números cuánticos opuestos. Los quarks son de espín1/2⁠ partículas, y por tanto fermiones . Cada quark o antiquark obedece la fórmula de Gell-Mann–Nishijima individualmente, por lo que cualquier ensamblaje aditivo de ellos también lo hará.

Los mesones están formados por un par de quarks de valencia y antiquarks (por lo tanto, tienen un número bariónico de 0), mientras que los bariones están formados por tres quarks (por lo tanto, tienen un número bariónico de 1). Este artículo analiza el modelo de quarks para los sabores up, down y strange de quarks (que forman una simetría SU(3) de sabor aproximada ). Existen generalizaciones para un mayor número de sabores.

Historia

El desarrollo de esquemas de clasificación para los hadrones se convirtió en una cuestión oportuna después de que nuevas técnicas experimentales descubrieran tantos de ellos que quedó claro que no todos podían ser elementales. Estos descubrimientos llevaron a Wolfgang Pauli a exclamar: "Si hubiera previsto eso, me habría dedicado a la botánica". y Enrico Fermi a aconsejar a su alumno Leon Lederman : "Joven, si pudiera recordar los nombres de estas partículas, habría sido botánico". Estos nuevos esquemas le valieron premios Nobel a físicos de partículas experimentales, incluido Luis Álvarez , quien estuvo a la vanguardia de muchos de estos desarrollos. Construir hadrones como estados ligados de menos constituyentes organizaría así el "zoológico" en cuestión. Varias propuestas tempranas, como las de Enrico Fermi y Chen-Ning Yang (1949), y el modelo de Sakata (1956), terminaron cubriendo satisfactoriamente los mesones, pero fallaron con los bariones, y por lo tanto no pudieron explicar todos los datos.

La fórmula de Gell-Mann–Nishijima , desarrollada por Murray Gell-Mann y Kazuhiko Nishijima , condujo a la clasificación de la Vía Óctuple , inventada por Gell-Mann, con importantes contribuciones independientes de Yuval Ne'eman , en 1961. Los hadrones se organizaron en multipletes de representación SU(3), octetos y decupletes, de aproximadamente la misma masa, debido a las interacciones fuertes; y diferencias de masa más pequeñas vinculadas a los números cuánticos de sabor, invisibles para las interacciones fuertes. La fórmula de masa de Gell-Mann–Okubo sistematizó la cuantificación de estas pequeñas diferencias de masa entre los miembros de un multiplete hadrónico, controlado por la ruptura explícita de simetría de SU(3).

El giro-3/2⁠
Ohmio⁻
El barión , un miembro del decuplete del estado fundamental, fue una predicción crucial de esa clasificación. Después de que se descubriera en un experimento en el Laboratorio Nacional de Brookhaven , Gell-Mann recibió un premio Nobel de física por su trabajo sobre el Camino Óctuple, en 1969.

Finalmente, en 1964, Gell-Mann y George Zweig discernieron de forma independiente lo que codifica la imagen de la Vía Óctuple: postularon tres constituyentes fermiónicos elementales (los quarks " up ", " down " y " strange ") que no se observan y posiblemente no se puedan observar en forma libre. Las combinaciones simples de pares o tripletes de estos tres constituyentes y sus antipartículas subyacen y codifican elegantemente la clasificación de la Vía Óctuple, en una estructura económica y ajustada, lo que resulta en una mayor simplicidad. Las diferencias de masa hadrónica ahora se vincularon a las diferentes masas de los quarks constituyentes.

Se necesitaría alrededor de una década para que la naturaleza inesperada -y la realidad física- de estos quarks se apreciara más plenamente (véase Quarks ). Contrariamente a la intuición, nunca se los puede observar de forma aislada ( confinamiento de color ), sino que siempre se combinan con otros quarks para formar hadrones completos, que luego proporcionan amplia información indirecta sobre los propios quarks atrapados. Por el contrario, los quarks sirven en la definición de cromodinámica cuántica , la teoría fundamental que describe completamente las interacciones fuertes; y ahora se entiende que la Vía Óctuple es una consecuencia de la estructura de simetría de sabor de los tres más ligeros de ellos.

Mesones

Figura 2 : Los mesones pseudoescalares de espín 0 forman un noneto

Figura 3 : Los mesones vectoriales de espín 1 forman un noneto

La clasificación de la vía óctuple recibe su nombre del siguiente hecho: si tomamos tres sabores de quarks, entonces los quarks se encuentran en la representación fundamental 3 ( llamada triplete) del sabor SU(3) . Los antiquarks se encuentran en la representación conjugada compleja 3. Los nueve estados (nonet) formados a partir de un par se pueden descomponer en la representación trivial 1 (llamada singlete) y la representación adjunta 8 ( llamada octeto ) . La notación para esta descomposición es

${\displaystyle \mathbf {3} \otimes \mathbf {\overline {3}} =\mathbf {8} \oplus \mathbf {1} ~.}$

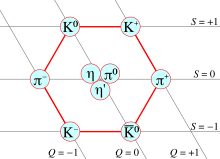
La figura 1 muestra la aplicación de esta descomposición a los mesones. Si la simetría de sabor fuera exacta (como en el límite en el que sólo operan las interacciones fuertes, pero las interacciones electrodébiles están nocionalmente desactivadas), entonces los nueve mesones tendrían la misma masa. Sin embargo, el contenido físico de la teoría completa ^{[ aclaración necesaria ]} incluye la consideración de la ruptura de simetría inducida por las diferencias de masa de los quarks y consideraciones de mezcla entre varios multipletes (como el octeto y el singlete).

NB Sin embargo, la división masiva entre los
η
y el
η′
es más grande de lo que el modelo de quarks puede admitir, y esto "
η
–
η′
El " rompecabezas " tiene su origen en peculiaridades topológicas del vacío de interacción fuerte, como las configuraciones instantáneas .

Los mesones son hadrones con número bariónico cero . Si el par quark-antiquark se encuentra en un estado de momento angular orbital L y tiene espín S , entonces

• | L − S | ≤ J ≤ L + S , donde S = 0 o 1,
• P = (−1) ^{L +1} , donde el 1 en el exponente surge de la paridad intrínseca del par quark-antiquark.
• C = (−1) ^{L + S} para los mesones que no tienen sabor . Los mesones con sabor tienen un valor indefinido de C.
• Para los estados isospín I = 1 y 0, se puede definir un nuevo número cuántico multiplicativo llamado G-paridad tal que G = (−1) ^{I + L + S} .

Si P = (−1) ^J , entonces se deduce que S = 1, por lo tanto PC = 1. Los estados con estos números cuánticos se denominan estados de paridad natural ; mientras que todos los demás números cuánticos se denominan exóticos (por ejemplo, el estado J ^PC = 0 ⁻⁻ ).

Bariones

Figura 4. La S = ⁠1/2Octeto bariónico en estado fundamental

Figura 5. La S = ⁠3/2 decuplete bariónico​

Dado que los quarks son fermiones , el teorema de estadística de espín implica que la función de onda de un barión debe ser antisimétrica bajo el intercambio de dos quarks cualesquiera. Esta función de onda antisimétrica se obtiene haciéndola completamente antisimétrica en color, discutida más adelante, y simétrica en sabor, espín y espacio juntos. Con tres sabores, la descomposición en sabor es El decuplete es simétrico en sabor, el singlete antisimétrico y los dos octetos tienen simetría mixta. Las partes de espacio y espín de los estados se fijan así una vez que se da el momento angular orbital. $${\displaystyle \mathbf {3} \otimes \mathbf {3} \otimes \mathbf {3} =\mathbf {10} _{S}\oplus \mathbf {8} _{M}\oplus \mathbf {8} _{M}\oplus \mathbf {1} _{A}~.}$$

A veces resulta útil pensar en los estados básicos de los quarks como los seis estados de tres sabores y dos espines por sabor. Esta simetría aproximada se denomina SU(6) de espín-sabor . En términos de esto, la descomposición es $${\displaystyle \mathbf {6} \otimes \mathbf {6} \otimes \mathbf {6} =\mathbf {56} _{S}\oplus \mathbf {70} _{M}\oplus \mathbf {70} _{M}\oplus \mathbf {20} _{A}~.}$$

Los 56 estados con combinación simétrica de espín y sabor se descomponen bajo el sabor SU(3) en donde el superíndice denota el espín, S , del barión. Dado que estos estados son simétricos en espín y sabor, también deberían ser simétricos en el espacio, una condición que se satisface fácilmente haciendo que el momento angular orbital sea L = 0 . Estos son los bariones del estado fundamental. $${\displaystyle \mathbf {56} =\mathbf {10} ^{\frac {3}{2}}\oplus \mathbf {8} ^{\frac {1}{2}}~,}$$

La S = ⁠1/2Los bariones octeto son los dos nucleones (
pag⁺
,
norte⁰
), las tres Sigmas (
Σ⁺
,
Σ⁰
,
Σ⁻
), los dos Xis (
Oh⁰
,
Oh⁻
), y la Lambda (
O⁰
). La S = ⁠3/2Los bariones decupletes son los cuatro deltas (
Δ⁺⁺
,
Δ⁺
,
Δ⁰
,
Δ⁻
), tres Sigmas (
Σ^∗+
,
Σ^∗0
,
Σ^∗−
), dos Xis (
Oh^∗0
,
Oh^∗−
), y el Omega (
Ohmio⁻
).

Por ejemplo, la función de onda del modelo de quarks constituyentes para el protón es $${\displaystyle |{\text{p}}_{\uparrow }\rangle ={\frac {1}{\sqrt {18}}}[2|{\text{u}}_{\uparrow }{\text{d}}_{\downarrow }{\text{u}}_{\uparrow }\rangle +2|{\text{u}}_{\uparrow }{\text{u}}_{\uparrow }{\text{d}}_{\downarrow }\rangle +2|{\text{d}}_{\downarrow }{\text{u}}_{\uparrow }{\text{u}}_{\uparrow }\rangle -|{\text{u}}_{\uparrow }{\text{u}}_{\downarrow }{\text{d}}_{\uparrow }\rangle -|{\text{u}}_{\uparrow }{\text{d}}_{\uparrow }{\text{u}}_{\downarrow }\rangle -|{\text{u}}_{\downarrow }{\text{d}}_{\uparrow }{\text{u}}_{\uparrow }\rangle -|{\text{d}}_{\uparrow }{\text{u}}_{\downarrow }{\text{u}}_{\uparrow }\rangle -|{\text{d}}_{\uparrow }{\text{u}}_{\uparrow }{\text{u}}_{\downarrow }\rangle -|{\text{u}}_{\downarrow }{\text{u}}_{\uparrow }{\text{d}}_{\uparrow }\rangle ]~.}$$

La mezcla de bariones, las divisiones de masa dentro y entre multipletes y los momentos magnéticos son algunas de las otras cantidades que el modelo predice con éxito.

El enfoque de la teoría de grupos descrito anteriormente supone que los quarks son ocho componentes de una única partícula, por lo que la antisimetrización se aplica a todos los quarks. Un enfoque más simple consiste en considerar los ocho quarks con sabor como ocho partículas separadas, distinguibles y no idénticas. En ese caso, la antisimetrización se aplica solo a dos quarks idénticos (como uu, por ejemplo). ^[6]

Luego, la función de onda del protón se puede escribir en una forma más simple:

${\displaystyle {\text{p}}\left({\frac {1}{2}},{\frac {1}{2}}\right)={\frac {{\text{u}}{\text{u}}{\text{d}}}{\sqrt {6}}}[2\uparrow \uparrow \downarrow -\uparrow \downarrow \uparrow -\downarrow \uparrow \uparrow ]}$

y el

${\displaystyle \Delta ^{+}\left({\frac {3}{3}},{\frac {3}{2}}\right)={\text{u}}{\text{u}}{\text{d}}[\uparrow \uparrow \uparrow ]~.}$

Si las interacciones quark-quark se limitan a interacciones de dos cuerpos, entonces se pueden derivar todas las predicciones exitosas del modelo de quarks, incluidas las reglas de suma para masas bariónicas y momentos magnéticos.

Descubrimiento del color

Los números cuánticos de color son las cargas características de la fuerza fuerte y no tienen ninguna relación con las interacciones electrodébiles. Se descubrieron como consecuencia de la clasificación del modelo de quarks, cuando se apreció que el espín S = ⁠3/2⁠ barión, el
Δ⁺⁺
, requería tres quarks up con espines paralelos y momento angular orbital nulo. Por lo tanto, no podía tener una función de onda antisimétrica (requerida por el principio de exclusión de Pauli ). Oscar Greenberg advirtió este problema en 1964, sugiriendo que los quarks deberían ser parafermiones . ^[7]

En cambio, seis meses después, Moo-Young Han y Yoichiro Nambu sugirieron la existencia de un grado de libertad oculto, al que denominaron grupo SU(3) (aunque más tarde lo llamaron "color"). Esto condujo a tres tripletes de quarks cuya función de onda era antisimétrica en el grado de libertad del color. El sabor y el color estaban entrelazados en ese modelo: no conmutaban. ^[8]

El concepto moderno de color que conmuta completamente con todas las demás cargas y proporciona la carga de fuerza fuerte fue articulado en 1973 por William Bardeen , Harald Fritzsch y Murray Gell-Mann . ^{[9] [10]}

Estados fuera del modelo de quarks

Si bien el modelo de quarks se puede derivar de la teoría de la cromodinámica cuántica , la estructura de los hadrones es más complicada de lo que permite este modelo. La función de onda mecánica cuántica completa de cualquier hadrón debe incluir pares de quarks virtuales, así como gluones virtuales , y permite una variedad de mezclas. Puede haber hadrones que se encuentren fuera del modelo de quarks. Entre estos se encuentran los "gluones" (que contienen solo gluones de valencia), los híbridos (que contienen quarks de valencia, así como gluones) y los hadrones exóticos (como los tetraquarks o pentaquarks ).

Véase también

• Partículas subatómicas
• Hadrones , bariones , mesones y quarks
• Hadrones exóticos : mesones exóticos y bariones exóticos
• Cromodinámica cuántica , sabor , el vacío QCD

Notas

1. Gell-Mann, M. (4 de enero de 1964). "Un modelo esquemático de bariones y mesones". Physics Letters . 8 (3): 214–215. Bibcode :1964PhL.....8..214G. doi :10.1016/S0031-9163(64)92001-3.
2. Zweig, G. (17 de enero de 1964). Un modelo SU(3) para la simetría de interacción fuerte y su ruptura (PDF) (Informe). Informe del CERN n.º 8182/TH.401.
3. Zweig, G. (1964). Un modelo SU(3) para la simetría de interacción fuerte y su ruptura: II (PDF) (Informe). Informe del CERN n.º 8419/TH.412.
4. Petermann, A. (1965). "Propriétés de l'étrangeté et une formule de masse pour les mésons vectoriels" [Propiedades de extrañeza y fórmula de masa para mesones vectoriales]. Física Nuclear . 63 (2): 349–352. arXiv : 1412.8681 . Código bibliográfico : 1965NucPh..63..349P. doi :10.1016/0029-5582(65)90348-2.
5. Petrov, Vladimir A. (23–27 de junio de 2014). Medio siglo con QUARKS . XXX Taller internacional sobre física de altas energías. Protvino , Óblast de Moscú , Rusia. arXiv : 1412.8681 .
6. Franklin, J. (1968). "Un modelo de bariones hecho de quarks con espín oculto". Physical Review . 172 (3): 1807–1817. Código Bibliográfico :1968PhRv..172.1807F. doi :10.1103/PhysRev.172.1807.
7. Greenberg, OW (1964). "Independencia de espín y espín unitario en un modelo de paraquark de bariones y mesones". Physical Review Letters . 13 (20): 598–602. Código Bibliográfico :1964PhRvL..13..598G. doi :10.1103/PhysRevLett.13.598.
8. Han, MY; Nambu, Y. (1965). "Modelo de tres tripletes con simetría doble SU(3)". Physical Review B . 139 (4B): 1006. Bibcode :1965PhRv..139.1006H. doi :10.1103/PhysRev.139.B1006.
9. Bardeen, W.; Fritzsch, H.; Gell-Mann, M. (1973). "Álgebra de corrientes de cono de luz, desintegración de π0 y aniquilación de e+ e−" . En Gatto, R. (ed.). Escala y simetría conforme en física de hadrones . John Wiley & Sons . pág. 139. arXiv : hep-ph/0211388 . Código Bibliográfico :2002hep.ph...11388B. ISBN. 0-471-29292-3.
10. Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. (1973). "Ventajas de la imagen de gluones en octeto de color". Physics Letters B . 47 (4): 365. Bibcode :1973PhLB...47..365F. CiteSeerX 10.1.1.453.4712 . doi :10.1016/0370-2693(73)90625-4. 

Referencias

• S. Eidelman et al. Particle Data Group (2004). "Revisión de la física de partículas" (PDF) . Physics Letters B . 592 (1–4): 1. arXiv : astro-ph/0406663 . Código Bibliográfico :2004PhLB..592....1P. doi :10.1016/j.physletb.2004.06.001. S2CID  118588567.
• Lichtenberg, DB (1970). Simetría unitaria y partículas elementales . Academic Press. ISBN 978-1483242729.
• Thomson, MA (2011), Notas de clase
• JJJ Kokkedee (1969). El modelo de los quarks . WA Benjamín . COMO EN  B001RAVDIA.