En geometría , un teseracto o 4-cubo es un hipercubo de cuatro dimensiones , análogo a un cuadrado bidimensional y a un cubo tridimensional . [1] Así como el perímetro del cuadrado consta de cuatro aristas y la superficie del cubo consta de seis caras cuadradas , la hipersuperficie del teseracto consta de ocho celdas cúbicas que se encuentran en ángulos rectos . El teseracto es uno de los seis 4 politopos regulares convexos .
El teseracto también se llama prisma cúbico , C 8 , octacorón (regular) o de 8 celdas . Es el politopo de medida de cuatro dimensiones , tomado como unidad de hipervolumen. [2] Coxeter lo denomina politopo γ 4 . [3] El término hipercubo sin una referencia de dimensión se trata con frecuencia como sinónimo de este politopo específico .
El Oxford English Dictionary remonta la palabra tesseract al libro de Charles Howard Hinton de 1888, A New Era of Thought . El término deriva del griego téssara ( τέσσαρα 'cuatro') y aktís ( ἀκτίς 'rayo'), refiriéndose a las cuatro aristas de cada vértice a otros vértices. Hinton originalmente deletreó la palabra como tessaract . [4]
Como politopo regular con tres cubos plegados alrededor de cada borde, tiene el símbolo de Schläfli {4,3,3} con simetría hiperoctaédrica de orden 384. Construido como un hiperprisma 4D hecho de dos cubos paralelos, puede denominarse Schläfli compuesto. símbolo {4,3} × { }, con orden de simetría 96. Como duoprisma 4-4 , un producto cartesiano de dos cuadrados , puede denominarse mediante un símbolo de Schläfli compuesto {4}×{4}, con orden de simetría 64 Como ortotopo , se puede representar mediante el símbolo de Schläfli compuesto { } × { } × { } × { } o { } 4 , con orden de simetría 16.
Dado que cada vértice de un teseracto es adyacente a cuatro aristas, la figura del vértice del teseracto es un tetraedro regular . El politopo dual del teseracto es el de 16 celdas con símbolo de Schläfli {3,3,4}, con el que se puede combinar para formar el compuesto de teseracto y 16 celdas .
Cada borde de un teseracto regular tiene la misma longitud. Esto es interesante cuando se utilizan teseractos como base para una topología de red para vincular múltiples procesadores en computación paralela : la distancia entre dos nodos es como máximo 4 y hay muchos caminos diferentes para permitir el equilibrio de peso.
Un teseracto está delimitado por ocho hiperplanos tridimensionales . Cada par de hiperplanos no paralelos se cruza para formar 24 caras cuadradas. Tres cubos y tres cuadrados se cruzan en cada arista. Hay cuatro cubos, seis cuadrados y cuatro aristas que se encuentran en cada vértice. En total, un teseracto consta de 8 cubos, 24 cuadrados, 32 aristas y 16 vértices.
Una unidad de teseracto tiene una longitud lateral de 1 y normalmente se toma como la unidad básica para el hipervolumen en un espacio de 4 dimensiones. La unidad teseracto en un sistema de coordenadas cartesiano para un espacio de 4 dimensiones tiene dos vértices opuestos en las coordenadas [0, 0, 0, 0] y [1, 1, 1, 1] , y otros vértices con coordenadas en todas las combinaciones posibles de 0. s y 1 s. Es el producto cartesiano del intervalo unitario cerrado [0, 1] en cada eje.
A veces un teseracto unitario está centrado en el origen, de modo que sus coordenadas son más simétricas. Este es el producto cartesiano del intervalo cerrado en cada eje.
Otro teseracto comúnmente conveniente es el producto cartesiano del intervalo cerrado [−1, 1] en cada eje, con vértices en las coordenadas (±1, ±1, ±1, ±1) . Este teseracto tiene una longitud de lado 2 y un hipervolumen 2 4 = 16 .
Al despliegue de un politopo se le llama red . Hay 261 redes distintas del teseracto. [5] Los despliegues del teseracto se pueden contar mapeando las redes en árboles emparejados (un árbol junto con una combinación perfecta en su complemento ).
.gif/1280px-From_Point_to_Tesseract_(Looped_Version).gif)
La construcción de hipercubos se puede imaginar de la siguiente manera:
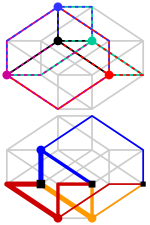
Las 8 celdas del teseracto pueden considerarse (de tres formas diferentes) como dos anillos entrelazados de cuatro cubos. [6]
El teseracto se puede descomponer en 4 politopos más pequeños. Es el casco convexo del compuesto de dos semiesseracts ( 16 celdas ). También se puede triangular en simples de 4 dimensiones ( 5 celdas irregulares ) que comparten sus vértices con el teseracto. Se sabe que existen92 487 256 tales triangulaciones [7] y que el menor número de símplices de 4 dimensiones en cualquiera de ellas es 16. [8]
La disección del teseracto en instancias de su simplex característico (un ortoesquema particular con diagrama de Coxeter
) es la construcción directa más básica posible del teseracto. La característica de 5 celdas del 4-cubo es una región fundamental del grupo de simetría definitorio del tesseract , el grupo que genera los politopos B 4 . El simplex característico del teseracto genera directamente el teseracto a través de las acciones del grupo, reflejándose en sus propias facetas delimitadoras (sus paredes de espejo ).
El radio de una hiperesfera circunscrita alrededor de un politopo regular es la distancia desde el centro del politopo a uno de los vértices, y para el teseracto este radio es igual a la longitud de su borde; el diámetro de la esfera, la longitud de la diagonal entre los vértices opuestos del teseracto, es el doble de la longitud del borde. Sólo unos pocos politopos uniformes tienen esta propiedad, incluido el teseracto de cuatro dimensiones y el de 24 celdas , el cuboctaedro tridimensional y el hexágono bidimensional . En particular, el teseracto es el único hipercubo (aparte de un punto de dimensión cero) que es radialmente equilátero . La diagonal más larga de vértice a vértice de un hipercubo de dimensiones unitarias es la que para el cuadrado es para el cubo y solo para el teseracto es la longitud de arista.
Un teseracto alineado con el eje inscrito en una esfera de 3 radios unitarios tiene vértices con coordenadas
Para un teseracto con longitud de lado s :
Esta matriz de configuración representa el teseracto. Las filas y columnas corresponden a vértices, aristas, caras y celdas. Los números diagonales dicen cuántos de cada elemento se encuentran en todo el teseracto. Los números no diagonales dicen cuántos elementos de la columna ocurren en o en el elemento de la fila. [9] Por ejemplo, el 2 en la primera columna de la segunda fila indica que hay 2 vértices en (es decir, en los extremos de) cada borde; el 4 en la segunda columna de la primera fila indica que 4 aristas se encuentran en cada vértice.
Es posible proyectar teseractos en espacios tridimensionales y bidimensionales, de manera similar a proyectar un cubo en un espacio bidimensional.
La proyección paralela de la primera celda del teseracto en el espacio tridimensional tiene una envoltura cúbica . Las celdas más cercanas y más alejadas se proyectan sobre el cubo, y las seis celdas restantes se proyectan sobre las seis caras cuadradas del cubo.
La proyección paralela del teseracto en el espacio tridimensional tiene una envoltura cúbica . Dos pares de celdas se proyectan hacia las mitades superior e inferior de esta envoltura, y las cuatro celdas restantes se proyectan hacia las caras laterales.
La proyección paralela de borde primero del teseracto en el espacio tridimensional tiene una envoltura en forma de prisma hexagonal . Seis celdas se proyectan sobre prismas rómbicos, que están dispuestos en el prisma hexagonal de una manera análoga a cómo las caras del cubo 3D se proyectan sobre seis rombos en una envoltura hexagonal bajo proyección de primer vértice. Las dos celdas restantes se proyectan sobre las bases del prisma.
La proyección paralela del primer vértice del teseracto en el espacio tridimensional tiene una envoltura dodecaédrica rómbica . Dos vértices del teseracto se proyectan hacia el origen. Hay exactamente dos formas de diseccionar un dodecaedro rómbico en cuatro romboedros congruentes , dando un total de ocho posibles romboedros, cada uno de los cuales es un cubo proyectado del teseracto. Esta proyección es también la de máximo volumen. Un conjunto de vectores de proyección es u = (1,1,−1,−1) , v = (−1,1,−1,1) , w = (1,−1,−1,1) .
El teseracto, como todos los hipercubos , tesela el espacio euclidiano . El panal teseractico autodual que consta de 4 teseractos alrededor de cada cara tiene el símbolo de Schläfli {4,3,3,4} . Por tanto, el teseracto tiene un ángulo diédrico de 90°. [10]
La simetría radial equilátera del teseracto convierte su teselación en la única red cúbica regular centrada en el cuerpo de esferas del mismo tamaño, en cualquier número de dimensiones.
El teseracto es el cuarto de una serie de hipercubos :
El teseracto (8 celdas) es el tercero de la secuencia de 6 4 politopos regulares convexos (en orden de tamaño y complejidad).
Como duoprisma uniforme , el teseracto existe en una secuencia de duoprismas uniformes : { p }×{4}.
El teseracto regular, junto con el de 16 celdas , existe en un conjunto de 15 4 politopos uniformes con la misma simetría . El teseracto {4,3,3} existe en una secuencia de 4 politopos y panales regulares , { p ,3,3} con figuras de vértices tetraédricos , {3,3}. El teseracto también está en una secuencia de 4 politopos regulares y panales , {4,3, p } con celdas cúbicas .
El politopo complejo regular 4 {4} 2 ,
, tiene una representación real como un teseracto o duoprisma 4-4 en un espacio de 4 dimensiones. 4 {4} 2 tiene 16 vértices y 8 4 aristas. Su simetría es 4 [4] 2 , orden 32. También tiene una construcción de simetría inferior,
, o 4 {}× 4 {}, con simetría 4 [2] 4 , orden 16. Esta es la simetría si los 4 bordes rojo y azul se consideran distintos. [11]
Desde su descubrimiento, los hipercubos de cuatro dimensiones han sido un tema popular en el arte, la arquitectura y la ciencia ficción. Ejemplos notables incluyen:
La palabra teseracto se adoptó más tarde para muchos otros usos en la cultura popular, incluso como recurso argumental en obras de ciencia ficción, a menudo con poca o ninguna conexión con el hipercubo de cuatro dimensiones; ver Tesseract (desambiguación) .
![{\displaystyle {\bigl [}{-{\tfrac {1}{2}}},{\tfrac {1}{2}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937dd70d7cd719d027e8e6f4d6f468ebe6e9dcb1)
