Teorema de Descartes

Ecuación para los radios de círculos tangentes

Círculos que se besan. Dados tres círculos tangentes entre sí ( negros ), en general hay dos posibles respuestas ( rojos ) en cuanto al radio que puede tener un cuarto círculo tangente.

En geometría , el teorema de Descartes establece que por cada cuatro círculos que se besan o que son tangentes entre sí , los radios de los círculos satisfacen una determinada ecuación cuadrática . Al resolver esta ecuación, se puede construir un cuarto círculo tangente a tres círculos dados que son tangentes entre sí. El teorema recibe su nombre de René Descartes , quien lo formuló en 1643.

El poema El beso de Frederick Soddy de 1936 resume con precisión el teorema en términos de las curvas (radios inversos con signo) de los cuatro círculos:

La suma de los cuadrados de las cuatro curvas
es la mitad del cuadrado de su suma ^[1]

Los casos especiales del teorema se aplican cuando uno o dos de los círculos se reemplazan por una línea recta (con curvatura cero) o cuando las curvas son números enteros o cuadrados . Una versión del teorema que utiliza números complejos permite calcular los centros de los círculos, y no solo sus radios. Con una definición apropiada de curvatura, el teorema también se aplica en geometría esférica y geometría hiperbólica . En dimensiones superiores, una ecuación cuadrática análoga se aplica a sistemas de esferas o hiperesferas tangentes por pares.

Historia

Los problemas geométricos que involucran círculos tangentes han sido considerados durante milenios. En la antigua Grecia del siglo III a. C., Apolonio de Perge dedicó un libro entero al tema, Ἐπαφαί [ Tangencias ]. Se ha perdido, y se conoce en gran parte a través de una descripción de su contenido por Pappus de Alejandría y a través de referencias fragmentarias a él en las matemáticas islámicas medievales . ^[2] Sin embargo, la geometría griega se centró en gran medida en la construcción con regla y compás . Por ejemplo, el problema de Apolonio , estrechamente relacionado con el teorema de Descartes, pide la construcción de un círculo tangente a tres círculos dados que no necesitan ser tangentes. ^[3] En cambio, el teorema de Descartes se formula utilizando relaciones algebraicas entre números que describen formas geométricas. Esto es característico de la geometría analítica , un campo iniciado por René Descartes y Pierre de Fermat en la primera mitad del siglo XVII. ^[4]

Descartes discutió brevemente el problema del círculo tangente en 1643, en dos cartas a la princesa Isabel del Palatinado . ^[5] Descartes inicialmente le planteó a la princesa el problema de Apolonio. Después de que los resultados parciales de Isabel revelaran que resolver el problema completo analíticamente sería demasiado tedioso, simplificó el problema al caso en el que los tres círculos dados son mutuamente tangentes, y al resolver este problema simplificado se le ocurrió la ecuación que describe la relación entre los radios, o curvaturas, de cuatro círculos tangentes por pares. Este resultado se conoció como el teorema de Descartes. ^{[6] [7]} Descartes no proporcionó el razonamiento a través del cual encontró esta relación. ^[8]

Las matemáticas japonesas frecuentemente se ocupaban de problemas que involucraban círculos y sus tangencias, ^[9] y el matemático japonés Yamaji Nushizumi formuló una forma del teorema del círculo de Descartes en 1751. Al igual que Descartes, lo expresó como una ecuación polinómica sobre los radios en lugar de sus curvaturas. ^{[10] [11]} El caso especial de este teorema para una línea recta y tres círculos fue registrado en una tablilla japonesa sangaku de 1824. ^[12]

El teorema de Descartes fue redescubierto en 1826 por Jakob Steiner , ^[13] en 1842 por Philip Beecroft, ^[14] y en 1936 por Frederick Soddy . Soddy eligió formatear su versión del teorema como un poema, The Kiss Precise , y lo publicó en Nature . Los círculos que se besan en este problema a veces se conocen como círculos de Soddy . Soddy también extendió el teorema a las esferas, ^[1] y en otro poema describió la cadena de seis esferas cada una tangente a sus vecinas y a tres esferas mutuamente tangentes dadas, una configuración ahora llamada hexlete de Soddy . ^{[15] [16]} Thorold Gosset y varios otros extendieron el teorema y el poema a dimensiones arbitrarias; la versión de Gosset se publicó al año siguiente. ^{[17] [18]} La generalización a veces se denomina teorema de Soddy-Gosset , ^[19] aunque tanto el hexlet como la versión tridimensional se conocían antes, en sangaku y en el trabajo de 1886 de Robert Lachlan. ^{[12] [20] [21]}

Se han publicado múltiples demostraciones del teorema. La demostración de Steiner utiliza cadenas de Pappus y el teorema de Viviani . Las demostraciones de Philip Beecroft y de HSM Coxeter implican cuatro círculos más, que pasan por ternas de tangencias de los tres círculos originales; Coxeter también proporcionó una demostración utilizando geometría inversa . Las demostraciones adicionales implican argumentos basados ​​en simetría, cálculos en álgebra exterior o manipulación algebraica de la fórmula de Heron (para la que véase § Círculos de Soddy de un triángulo). ^{[22] [23]} El resultado también se desprende de la observación de que el determinante de Cayley-Menger de los cuatro centros de círculos coplanares es cero. ^[24]

Declaración

Aquí, como los tres círculos son tangentes entre sí en el mismo punto, el teorema de Descartes no se aplica.

El teorema de Descartes se expresa más fácilmente en términos de las curvaturas de los círculos . ^[25] La curvatura con signo (o doblez ) de un círculo se define como , ${\displaystyle k=\pm 1/r}$ donde es su radio. Cuanto más grande sea un círculo, menor será la magnitud de su curvatura, y viceversa. El signo en (representado por el símbolo ) es positivo para un círculo que es tangente externamente a los otros círculos. Para un círculo tangente internamente que circunscribe a los otros círculos, el signo es negativo. Si una línea recta se considera un círculo degenerado con curvatura cero (y, por lo tanto, radio infinito), el teorema de Descartes también se aplica a una línea y tres círculos que son los tres mutuamente tangentes (véase Círculo generalizado ). ^[1] ${\displaystyle r}$ ${\displaystyle k=\pm 1/r}$ ${\displaystyle \pm }$

Para cuatro círculos que son tangentes entre sí en seis puntos distintos, con curvaturas para , el teorema de Descartes dice: ${\displaystyle k_{i}}$ ${\displaystyle i=1,\dots ,4}$

Si se considera que una de las cuatro curvaturas es una variable y el resto son constantes, se trata de una ecuación cuadrática . Para hallar el radio de un cuarto círculo tangente a tres círculos dados que se besan, la ecuación cuadrática se puede resolver como ^{[13] [26]}

El símbolo indica que, en general, esta ecuación tiene dos soluciones y cualquier triple de círculos tangentes tiene dos círculos tangentes (o líneas rectas degeneradas). Los criterios específicos del problema pueden favorecer una de estas dos soluciones sobre la otra en cualquier problema dado. ^[22] ${\displaystyle \pm }$

El teorema no se aplica a sistemas de círculos con más de dos círculos tangentes entre sí en el mismo punto. Requiere que los puntos de tangencia sean distintos. ^[8] Cuando más de dos círculos son tangentes en un único punto, puede haber infinitos círculos de este tipo, con curvaturas arbitrarias; véase lápiz de círculos . ^[27]

Localización de los centros del círculo

Para determinar completamente un círculo, no sólo se debe conocer su radio (o curvatura), sino también su centro. La ecuación pertinente se expresa con mayor claridad si las coordenadas cartesianas se interpretan como un número complejo . La ecuación entonces parece similar al teorema de Descartes y por lo tanto se llama teorema complejo de Descartes . Dados cuatro círculos con curvaturas y centros para , se cumple la siguiente igualdad además de la ecuación (1) : ${\displaystyle (x,y)}$ ${\displaystyle z=x+iy}$ ${\displaystyle k_{i}}$ ${\displaystyle z_{i}}$ ${\displaystyle i\in \{1,2,3,4\}}$

Una vez hallada la ecuación (2) , se puede proceder a calcular resolviendo la ecuación (3) como una ecuación cuadrática, obteniéndose una forma similar a la ecuación (2) : ${\displaystyle k_{4}}$ ${\displaystyle z_{4}}$

$${\displaystyle z_{4}={\frac {z_{1}k_{1}+z_{2}k_{2}+z_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}z_{1}z_{2}+k_{2}k_{3}z_{2}z_{3}+k_{1}k_{3}z_{1}z_{3}}}}{k_{4}}}.}$$

Nuevamente, en general, hay dos soluciones para ${\displaystyle z_{4}}$ que corresponden a las dos soluciones para . ${\displaystyle k_{4}}$ El signo más/menos en la fórmula anterior para ${\displaystyle z_{4}}$ no corresponde necesariamente al signo más/menos en la fórmula para . ^{[19] [28] [29]} ${\displaystyle k_{4}}$

Casos especiales

Tres círculos congruentes mutuamente tangentes de curvaturas k = 1/√3 son todos tangentes a dos círculos de curvaturas respectivas k = √3 ± 2 .

Tres círculos congruentes

Cuando tres de los cuatro círculos son congruentes, sus centros forman un triángulo equilátero, al igual que sus puntos de tangencia. Las dos posibilidades para un cuarto círculo tangente a los tres son concéntricas, y la ecuación (2) se reduce a ^[30]

$${\displaystyle k_{4}=(3\pm 2{\sqrt {3}})k_{1}.}$$

Una o más líneas rectas

El teorema de Descartes todavía se aplica cuando uno de los círculos se reemplaza por una línea recta de curvatura cero.

Si uno de los tres círculos se reemplaza por una línea recta tangente a los círculos restantes , entonces su curvatura es cero y se elimina de la ecuación (1). Por ejemplo, si , ${\displaystyle k_{3}=0}$ entonces la ecuación (1) se puede factorizar como ^[31]

$${\displaystyle {\begin{aligned}&{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}+{\sqrt {k_{4}}}{\bigr )}{\bigl (}{{\sqrt {k_{2}}}+{\sqrt {k_{4}}}-{\sqrt {k_{1}}}}{\bigr )}\\[3mu]&\quad {}\cdot {\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{4}}}-{\sqrt {k_{2}}}{\bigr )}{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}-{\sqrt {k_{4}}}{\bigr )}=0,\end{aligned}}}$$

y la ecuación (2) se simplifica a ^[32]

$${\displaystyle k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.}$$

Tomando la raíz cuadrada de ambos lados se llega a otra formulación alternativa de este caso (con ), ${\displaystyle k_{1}\geq k_{2}}$

$${\displaystyle {\sqrt {k_{4}}}={\sqrt {k_{1}}}\pm {\sqrt {k_{2}}},}$$

que ha sido descrito como "una especie de versión demente del teorema de Pitágoras ". ^[25]

Si se sustituyen dos círculos por líneas rectas, la tangencia entre los dos círculos sustituidos se convierte en un paralelismo entre sus dos líneas de sustitución. En este caso, con , ${\displaystyle k_{2}=k_{3}=0}$ la ecuación (2) se reduce a la trivialidad

$${\displaystyle \displaystyle k_{4}=k_{1}.}$$

Esto corresponde a la observación de que, para que las cuatro curvas permanezcan mutuamente tangentes, los otros dos círculos deben ser congruentes. ^{[19] [26]}

Curvaturas enteras

Una junta apolínea con curvaturas enteras, generada por cuatro círculos mutuamente tangentes con curvaturas −10 (el círculo exterior), 18, 23 y 27

Cuando cuatro círculos tangentes descritos por la ecuación (2) tienen curvaturas enteras, el cuarto círculo alternativo descrito por la segunda solución de la ecuación también debe tener una curvatura entera. Esto se debe a que ambas soluciones difieren de un entero por la raíz cuadrada de un entero, y por lo tanto, cualquiera de las soluciones solo puede ser un entero si esta raíz cuadrada, y por lo tanto la otra solución, también es un entero. Cada cuatro enteros que satisfacen la ecuación en el teorema de Descartes forman las curvaturas de cuatro círculos tangentes. ^[33] Los cuádruples enteros de este tipo también están estrechamente relacionados con los triángulos heronianos , triángulos con lados y área enteros. ^[34]

Partiendo de cuatro círculos tangentes entre sí, y reemplazando repetidamente uno de los cuatro por su solución alternativa ( salto de Vieta ), de todas las formas posibles, se llega a un sistema de infinitos círculos tangentes llamado junta apolínea . Cuando los cuatro círculos iniciales tienen curvaturas enteras, también las tiene cada reemplazo y, por lo tanto, todos los círculos de la junta tienen curvaturas enteras. Cuatro círculos tangentes cualesquiera con curvaturas enteras pertenecen exactamente a una de esas juntas, descrita de forma única por su raíz cuádruple de los cuatro círculos más grandes y las cuatro curvaturas más pequeñas. Esta raíz cuádruple se puede hallar, a partir de cualquier otra raíz cuádruple de la misma junta, reemplazando repetidamente el círculo más pequeño por uno más grande que resuelva la misma ecuación de Descartes, hasta que no sea posible tal reducción. ^[33]

Se dice que un cuádruple raíz es primitivo si no tiene divisor común no trivial . Todo cuádruple raíz primitivo se puede encontrar a partir de una factorización de una suma de dos cuadrados, , como el cuádruple . Para ser primitivo, debe satisfacer las condiciones adicionales , y . Las factorizaciones de sumas de dos cuadrados se pueden obtener utilizando el teorema de la suma de dos cuadrados . Cualquier otra junta apolínea entera se puede formar multiplicando un cuádruple raíz primitivo por un entero arbitrario, y cualquier cuádruple en una de estas juntas (es decir, cualquier solución entera a la ecuación de Descartes) se puede formar invirtiendo el proceso de reemplazo utilizado para encontrar el cuádruple raíz. Por ejemplo, la junta con cuádruple raíz , que se muestra en la figura, se genera de esta manera a partir de la suma factorizada de dos cuadrados . ^[33] ${\displaystyle n^{2}+m^{2}=de}$ ${\displaystyle (-n,\,d+n,\,e+n,\,d+e+n-2m)}$ ${\displaystyle \gcd(n,d,e)=1}$ ${\displaystyle -n\leq 0\leq 2m\leq d\leq e}$ ${\displaystyle (-10,18,23,27)}$ ${\displaystyle 10^{2}+2^{2}=8\cdot 13}$

Círculos de Ford

Círculos de Ford en el intervalo unitario

Los casos especiales de una línea recta y curvaturas enteras se combinan en los círculos de Ford . Estos son una familia infinita de círculos tangentes al eje y del sistema de coordenadas cartesianas en sus puntos racionales. Cada fracción (en términos mínimos) tiene un círculo tangente a la línea en el punto con curvatura . Tres de estas curvaturas, junto con la curvatura cero del eje, cumplen las condiciones del teorema de Descartes siempre que los denominadores de dos de las fracciones correspondientes sumen el denominador de la tercera. Los dos círculos de Ford para las fracciones y (ambos en términos mínimos) son tangentes cuando . Cuando son tangentes, forman un cuádruple de círculos tangentes con el eje y con el círculo por su mediante . ^[35] ${\displaystyle x}$ ${\displaystyle p/q}$ ${\displaystyle (p/q,0)}$ ${\displaystyle 2q^{2}}$ ${\displaystyle p/q}$ ${\displaystyle r/s}$ ${\displaystyle |ps-qr|=1}$ ${\displaystyle x}$ ${\displaystyle (p+r)/(q+s)}$

Los círculos de Ford pertenecen a una junta apolínea especial con raíz cuádruple , ${\displaystyle (0,0,1,1)}$ delimitada entre dos líneas paralelas, que pueden tomarse como el eje y la línea . Esta es la única junta apolínea que contiene una línea recta, y no está delimitada dentro de un círculo de curvatura negativa. Los círculos de Ford son los círculos en esta junta que son tangentes al eje y . ^[33] ${\displaystyle x}$ ${\displaystyle y=1}$ ${\displaystyle x}$

Progresión geométrica

Sucesión loxodrómica de círculos tangentes de Coxeter . Cada círculo está etiquetado con un entero i , su posición en la sucesión; tiene radio ρ ⁱ y curvatura ρ ⁻ⁱ .

Cuando se supone que los cuatro radios de los círculos del teorema de Descartes están en una progresión geométrica con razón , ${\displaystyle \rho }$ las curvaturas también están en la misma progresión (en sentido inverso). Al introducir esta razón en el teorema se obtiene la ecuación

$${\displaystyle 2(1+\rho ^{2}+\rho ^{4}+\rho ^{6})=(1+\rho +\rho ^{2}+\rho ^{3})^{2},}$$

que tiene sólo una solución real mayor que uno, la razón

$${\displaystyle \rho =\varphi +{\sqrt {\varphi }}\approx 2.89005\ ,}$$

donde es la proporción áurea . Si se continúa la misma progresión en ambas direcciones, cada cuatro números consecutivos describen círculos que obedecen al teorema de Descartes. La progresión geométrica de círculos de doble extremo resultante se puede organizar en un único patrón espiral de círculos tangentes , llamado secuencia loxodrómica de círculos tangentes de Coxeter . Fue descrita por primera vez, junto con construcciones análogas en dimensiones superiores, por HSM Coxeter en 1968. ^{[36] [37]} ${\displaystyle \varphi }$

Círculos de barro de un triángulo

Cualquier triángulo en el plano tiene tres círculos tangentes externamente centrados en sus vértices. Dejando ser los tres puntos, ser las longitudes de los lados opuestos, y ser el semiperímetro , estos tres círculos tienen radios . Por el teorema de Descartes, dos círculos más, a veces llamados círculos de Soddy , son tangentes a estos tres círculos. Están separados por el incírculo , uno interior a él y uno exterior. ^{[38] [39] [40]} El teorema de Descartes se puede utilizar para mostrar que la curvatura del círculo de Soddy interior es , donde es el área del triángulo, es su circunradio y es su inradio . El círculo de Soddy exterior tiene curvatura . ^[41] La curvatura interior es siempre positiva, pero la curvatura exterior puede ser positiva, negativa o cero. Los triángulos cuyo círculo exterior degenera en una línea recta con curvatura cero se han llamado "triángulos soddyianos". ^[41] ${\displaystyle A,B,C}$ ${\displaystyle a,b,c}$ ${\textstyle s={\tfrac {1}{2}}(a+b+c)}$ ${\displaystyle s-a,s-b,s-c}$ ${\textstyle (4R+r+2s)/\Delta }$ ${\displaystyle \Delta }$ ${\displaystyle R}$ ${\displaystyle r}$ ${\textstyle (4R+r-2s)/\Delta }$

Cuatro triángulos con vértices en los centros de los círculos de Soddy

Una de las muchas demostraciones del teorema de Descartes se basa en esta conexión con la geometría de triángulos y en la fórmula de Herón para el área de un triángulo en función de las longitudes de sus lados. Si tres círculos son tangentes externamente, con radios , entonces sus centros forman los vértices de un triángulo con longitudes de lados y semiperímetro. Según la fórmula de Herón, este triángulo tiene área ${\displaystyle r_{1},r_{2},r_{3},}$ ${\displaystyle P_{1},P_{2},P_{3}}$ ${\displaystyle r_{1}+r_{2},}$ ${\displaystyle r_{1}+r_{3},}$ ${\displaystyle r_{2}+r_{3},}$ ${\displaystyle r_{1}+r_{2}+r_{3}.}$ ${\displaystyle \triangle P_{1}P_{2}P_{3}}$

$${\displaystyle {\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}.}$$

Consideremos ahora el círculo interior de Soddy cuyo radio está centrado en el punto interior del triángulo. El triángulo se puede dividir en tres triángulos más pequeños y cuyas áreas se pueden obtener sustituyendo uno de los otros radios en la fórmula del área anterior. El área del primer triángulo es igual a la suma de estas tres áreas: ${\displaystyle r_{4},}$ ${\displaystyle P_{4}}$ ${\displaystyle \triangle P_{1}P_{2}P_{3}}$ ${\displaystyle \triangle P_{1}P_{2}P_{4},}$ ${\displaystyle \triangle P_{4}P_{2}P_{3},}$ ${\displaystyle \triangle P_{1}P_{4}P_{3},}$ ${\displaystyle r_{4}}$

$${\displaystyle {\begin{aligned}{\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}={}&{\sqrt {r_{1}r_{2}r_{4}(r_{1}+r_{2}+r_{4})}}+{}\\&{\sqrt {r_{1}r_{3}r_{4}(r_{1}+r_{3}+r_{4})}}+{}\\&{\sqrt {r_{2}r_{3}r_{4}(r_{2}+r_{3}+r_{4})}}.\end{aligned}}}$$

Una manipulación algebraica cuidadosa muestra que esta fórmula es equivalente a la ecuación (1) , el teorema de Descartes. ^[22]

Aquí el centro exterior de Soddy se encuentra fuera del triángulo.

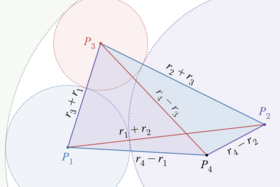
Este análisis cubre todos los casos en los que cuatro círculos son tangentes externamente; uno es siempre el círculo Soddy interior de los otros tres. Los casos en los que uno de los círculos es tangente internamente a los otros tres y forma su círculo Soddy exterior son similares. Nuevamente los cuatro centros forman cuatro triángulos, pero (siendo el centro del círculo Soddy exterior) los lados del triángulo que tienen longitudes que son diferencias de radios, y no sumas. pueden estar dentro o fuera del triángulo formado por los otros tres centros; cuando está dentro, el área de este triángulo es igual a la suma de las otras tres áreas de los triángulos, como se indicó anteriormente. Cuando está fuera, el cuadrilátero formado por los cuatro centros puede subdividirse por una diagonal en dos triángulos, de dos maneras diferentes, dando una igualdad entre la suma de las áreas de dos triángulos y la suma de las áreas de los otros dos triángulos. En todos los casos, la ecuación del área se reduce al teorema de Descartes. Este método no se aplica directamente a los casos en los que uno de los círculos degenera en una línea, pero estos pueden manejarse como un caso límite de círculos. ^[22] ${\displaystyle P_{1},P_{2},P_{3},P_{4}}$ ${\displaystyle P_{4}}$ ${\displaystyle P_{4}}$ ${\displaystyle r_{4}-r_{1},}$ ${\displaystyle r_{4}-r_{1},}$ ${\displaystyle r_{4}-r_{3},}$ ${\displaystyle P_{4}}$

Generalizaciones

Configuraciones arbitrarias de cuatro círculos

El teorema de Descartes se puede expresar como una ecuación matricial y luego generalizarse a otras configuraciones de cuatro círculos orientados modificando la matriz. Sea un vector columna de las cuatro curvaturas de los círculos y sea una matriz simétrica cuyos coeficientes representan la orientación relativa entre los círculos orientados i y j en su punto de intersección: ${\displaystyle \mathbf {k} }$ ${\displaystyle \mathbf {Q} }$ ${\displaystyle q_{i,j}}$ $${\displaystyle \mathbf {Q} ={\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}},\qquad \mathbf {Q} ^{-1}={\frac {1}{4}}{\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}}.}$$

Luego la ecuación (1) puede reescribirse como la ecuación matricial ^{[19] [42]}

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0.}$$

Como generalización del teorema de Descartes, una matriz simétrica modificada puede representar cualquier configuración deseada de cuatro círculos reemplazando cada coeficiente con la inclinación entre dos círculos, definida como ${\displaystyle \mathbf {Q} }$ ${\displaystyle q_{i,j}}$

$${\displaystyle q_{i,j}={\frac {r_{i}^{2}+r_{j}^{2}-d_{i,j}^{2}}{2r_{i}r_{j}}},}$$

donde son los radios respectivos de los círculos, y es la distancia euclidiana entre sus centros. ^{[43] [44] [45]} Cuando los círculos se intersecan, , el coseno del ángulo de intersección entre los círculos. La inclinación, a veces llamada distancia inversa , es cuando los círculos son tangentes y están orientados de la misma manera en su punto de tangencia, cuando los dos círculos son tangentes y están orientados de manera opuesta en el punto de tangencia, para círculos ortogonales , fuera del intervalo para círculos que no se intersecan, y en el límite cuando un círculo degenera en un punto. ^{[42] [37]} ${\displaystyle r_{i},r_{j}}$ ${\displaystyle d_{i,j}}$ ${\displaystyle q_{i,j}=\cos(\theta _{i,j})}$ ${\displaystyle 1}$ ${\displaystyle -1}$ ${\displaystyle 0}$ ${\displaystyle [-1,1]}$ ${\displaystyle \infty }$

La ecuación se satisface para cualquier configuración arbitraria de cuatro círculos en el plano, siempre que se cuente con la matriz apropiada de inclinaciones por pares. ^[42] ${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0}$ ${\displaystyle \mathbf {Q} }$

Geometría esférica e hiperbólica

Un caso especial del teorema de Descartes sobre la esfera tiene tres círculos de radio 60° ( k = 1/√3 , en azul) para los cuales ambos círculos que tocan a los tres (en verde) tienen el mismo radio ( 30° , k = √3 ).

El teorema de Descartes se generaliza a círculos grandes o pequeños mutuamente tangentes en geometría esférica si la curvatura del círculo ésimo se define como la curvatura geodésica del círculo relativa a la esfera, que es igual a la cotangente del radio intrínseco orientado. Entonces: ^{[19] [44]} ${\displaystyle j}$ ${\textstyle k_{j}=\cot \rho _{j},}$ ${\displaystyle \rho _{j}.}$

$${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})+4.}$$

Resolviendo una de las curvaturas en términos de las otras tres,

$${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}-1}}.}$$

Como ecuación matricial,

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =-1.}$$

La cantidad es el "diámetro estereográfico" de un círculo pequeño. Se trata de la longitud euclidiana del diámetro en el plano proyectado estereográficamente cuando algún punto del círculo se proyecta hacia el origen. Para un círculo máximo, dicha proyección estereográfica es una línea recta que pasa por el origen, por lo que . ^[46] ${\displaystyle 1/k_{j}=\tan \rho _{j}}$ ${\displaystyle k_{j}=0}$

Cuatro círculos generalizados a través del origen del modelo del disco de Poincaré del plano hiperbólico: círculo (azul), horociclo (rojo), hiperciclo (violeta) y geodésico (verde). El límite de los puntos ideales se representa con un trazo discontinuo y la región sombreada está fuera del plano.

De la misma manera, el teorema se generaliza a círculos mutuamente tangentes en geometría hiperbólica si la curvatura del ciclo n se define como la curvatura geodésica del círculo relativa al plano hiperbólico, la cotangente hiperbólica del radio intrínseco orientado . Entonces: ^{[19] [44]} ${\displaystyle j}$ ${\textstyle k_{j}=\coth \rho _{j},}$ ${\displaystyle \rho _{j}.}$

$${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})-4.}$$

Resolviendo una de las curvaturas en términos de las otras tres,

$${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}+1}}.}$$

Como ecuación matricial,

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =1.}$$

Esta fórmula también es válida para configuraciones mutuamente tangentes en geometría hiperbólica, incluidos hiperciclos y horociclos , si es la curvatura geodésica del ciclo con respecto al plano hiperbólico, el recíproco del diámetro estereográfico del ciclo. Este es el diámetro bajo proyección estereográfica (el modelo de disco de Poincaré ) cuando un punto final del diámetro se proyecta al origen. ^[47] Los hiperciclos no tienen un centro bien definido o un radio intrínseco y los horociclos tienen un punto ideal para un centro y un radio intrínseco infinito, pero para un círculo hiperbólico, para un horociclo, para un hiperciclo y para una geodésica . ^[48] ${\displaystyle k_{j}}$ ${\displaystyle |k_{j}|>1}$ ${\displaystyle |k_{j}|=1}$ ${\displaystyle |k_{j}|<1}$ ${\displaystyle k_{j}=0}$

Dimensiones superiores

Hexlet de Soddy . Cualquier par de esferas verdes adyacentes junto con las dos esferas rojas y la esfera gris exterior satisfacen el caso tridimensional del teorema de Descartes.

En el espacio euclidiano de dimensión 1 , el número máximo de hiperesferas mutuamente tangentes es . Por ejemplo, en el espacio tridimensional, cinco esferas pueden ser mutuamente tangentes. Las curvaturas de las hiperesferas satisfacen ${\displaystyle n}$ ${\displaystyle n+2}$

$${\displaystyle {\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=n\,\sum _{i=1}^{n+2}k_{i}^{2}}$$

con el caso correspondiente a un hiperplano plano, generalizando la versión bidimensional del teorema. ^{[19] [44]} Aunque no existe un análogo tridimensional de los números complejos, la relación entre las posiciones de los centros se puede reexpresar como una ecuación matricial , que también se generaliza a dimensiones. ^[19] ${\displaystyle k_{i}=0}$ ${\displaystyle n}$

En tres dimensiones, supongamos que se fijan tres esferas mutuamente tangentes y se da una cuarta esfera, tangente a las tres esferas fijas. La versión tridimensional del teorema de Descartes se puede aplicar para encontrar una esfera tangente a y a las esferas fijas, y luego se puede aplicar de nuevo para encontrar una nueva esfera tangente a y a las esferas fijas, y así sucesivamente. El resultado es una secuencia cíclica de seis esferas, cada una tangente a sus vecinas en la secuencia y a las tres esferas fijas, una configuración llamada hexlete de Soddy , después del descubrimiento de Soddy y su publicación en forma de otro poema en 1936. ^{[15] [16]} ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{3}}$ ${\displaystyle S_{2}}$

Las configuraciones de dimensiones superiores de hiperesferas mutuamente tangentes en geometría esférica o hiperbólica, con curvaturas definidas como anteriormente, satisfacen

$${\displaystyle {\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=nC+n\,\sum _{i=1}^{n+2}k_{i}^{2},}$$

donde en geometría esférica y en geometría hiperbólica. ^{[44] [19]} ${\displaystyle C=2}$ ${\displaystyle C=-2}$

Véase también

• Empaquetado circular en un círculo
• Identidad de cuatro cuadrados de Euler
• Círculos de Malfatti

Referencias

1. Soddy, F. (junio de 1936), "El beso preciso", Nature , 137 (3477): 1021, Bibcode :1936Natur.137.1021S, doi : 10.1038/1371021a0 , S2CID  6012051
2. Hogendijk, Jan P. (1986), "Huellas árabes de las obras perdidas de Apolonio", Archivo de Historia de las Ciencias Exactas , 35 (3): 187–253, doi :10.1007/BF00357307, JSTOR  41133783, MR  0851067, S2CID  121613986
3. Court, Nathan Altshiller (octubre de 1961), "El problema de Apolonio", The Mathematics Teacher , 54 (6): 444–452, doi :10.5951/MT.54.6.0444, JSTOR  27956431
4. Boyer, Carl B. (2004) [1956], "Capítulo 5: Fermat y Descartes", Historia de la geometría analítica , Dover Publications, págs. 74-102, ISBN 978-0-486-43832-0
5. Descartes, René (1901), Adán, Charles; Tannery, Paul (eds.), Oeuvres de Descartes (en francés), vol. 4: Correspondencia Juillet 1643 – Abril 1647, París: Léopold Cerf, "325. Descartes a Elisabeth", págs. 37–42; "328. Descartes a Isabel", págs. 45-50
   Bos, Erik-Jan (2010), "La princesa Isabel de Bohemia y las cartas de Descartes (1650-1665)", Historia Mathematica , 37 (3): 485-502, doi : 10.1016/j.hm.2009.11.004
6. Shapiro, Lisa (2007), La correspondencia entre la princesa Isabel de Bohemia y René Descartes , La otra voz en la Europa moderna temprana, University of Chicago Press, pp. 37–39, 73–77, ISBN 978-0-226-20444-4
7. Mackenzie, Dana (marzo-abril de 2023), "La princesa y el filósofo", American Scientist , vol. 111, núm. 2, págs. 80-84, ProQuest  2779946948
8. Coxeter, HSM (enero de 1968), "El problema de Apolonio", The American Mathematical Monthly , 75 (1): 5–15, doi :10.1080/00029890.1968.11970941, JSTOR  2315097
9. Yanagihara, K. (1913), "Sobre algunas proposiciones geométricas en Wasan, la matemática nativa japonesa", Tohoku Mathematical Journal , 3 : 87–95, JFM  44.0052.02
10. Michiwaki, Yoshimasa (2008), "Geometría en las matemáticas japonesas", en Selin, Helaine (ed.), Enciclopedia de la historia de la ciencia, la tecnología y la medicina en culturas no occidentales , Springer Netherlands, págs. 1018-1019, doi :10.1007/978-1-4020-4425-0_9133, ISBN 978-1-4020-4559-2
11. Takinami, Susumu; Michiwaki, Yoshimasa (1984), "Sobre el teorema del círculo de Descartes" (PDF) , Journal for History of Mathematics , 1 (1), Sociedad Coreana de Historia de las Matemáticas: 1–8
12. Rothman, Tony ; Fugakawa, Hidetoshi (mayo de 1998), "Geometría del templo japonés", Scientific American , 278 (5): 84–91, Bibcode :1998SciAm.278e..84R, doi :10.1038/scientificamerican0598-84, JSTOR  26057787; ver ilustración superior, pág. 86. Otra tablilla de 1822 (centro, pág. 88) se refiere al hexlet de Soddy , una configuración de esferas tangentes tridimensionales.
13. Steiner, Jakob (enero de 1826), "Fortsetzung der geometrischen Betrachtungen (Heft 2, S. 161)", Journal für die reine und angewandte Mathematik , 1826 (1), págs. 252–288, fig. 2–25 taf. III, doi :10.1515/crll.1826.1.252, S2CID  121590578
14. Beecroft, Philip (1842), "Propiedades de los círculos en contacto mutuo", Diario de damas y caballeros (139): 91–96
15. Soddy, Frederick (diciembre de 1936), "El hexlet", Nature , 138 (3501): 958, Bibcode :1936Natur.138..958S, doi : 10.1038/138958a0 , S2CID  28170211
16. Barnes, John (2012), "El hexlet de Soddy", Gems of Geometry (2.ª ed.), Heidelberg: Springer, págs. 173-177, doi :10.1007/978-3-642-30964-9, ISBN 978-3-642-30963-2, Sr.  2963305
17. Gardner, Martin (mayo de 1968), "Juegos matemáticos: círculos y esferas, y cómo se besan y se empaquetan", Scientific American , 218 (5): 130–139, doi :10.1038/scientificamerican0568-130, JSTOR  24926234
18. "El beso preciso", Nature , 139 (3506): 62, enero de 1937, Bibcode :1937Natur.139Q..62., doi : 10.1038/139062a0
19. Lagarias, Jeffrey C. ; Mallows, Colin L. ; Wilks, Allan R. (2002), "Más allá del teorema del círculo de Descartes", The American Mathematical Monthly , 109 (4): 338–361, arXiv : math/0101066 , doi :10.2307/2695498, JSTOR  2695498, MR  1903421
20. Hidetoshi, Fukagawa; Kazunori, Horibe (2014), "Sangaku: matemáticas y arte japoneses en los siglos XVIII, XIX y XX", en Greenfield, Gary; Hart, George; Sarhangi, Reza (eds.), Bridges Seoul Conference Proceedings , Tessellations Publishing, págs. 111-118
21. Lachlan, R. (1886), "Sobre sistemas de círculos y esferas", Philosophical Transactions of the Royal Society of London , 177 : 481–625, JSTOR  109492; ver "Esferas en contacto entre sí", págs. 585-587
22. Levrie, Paul (2019), "Una prueba sencilla del teorema del círculo de Descartes", The Mathematical Intelligencer , 41 (3): 24–27, doi :10.1007/s00283-019-09883-x, hdl : 10067/1621880151162165141 , MR  3995314, S2CID  253818666
23. Pedoe, Daniel (1967), "Sobre un teorema en geometría", The American Mathematical Monthly , 74 (6): 627–640, doi :10.2307/2314247, JSTOR  2314247, MR  0215169
24. Bradford, Alden (2023), "Una prueba aún más sencilla del teorema del círculo de Descartes", The Mathematical Intelligencer , 45 (3): 263–265, arXiv : 2211.05539 , doi :10.1007/s00283-022-10234-6, MR  4645170
25. Mackenzie, Dana (enero-febrero de 2010), "A tisket, a tasket, an Apollonian gasket", Computing Science, American Scientist , vol. 98, no. 1, pp. 10-14, JSTOR  27859441, Todos estos recíprocos parecen un poco extravagantes, por lo que la fórmula suele simplificarse escribiéndola en términos de las curvaturas o las curvaturas de los círculos.
26. Wilker, JB (1969), "Cuatro pruebas de una generalización del teorema del círculo de Descartes", The American Mathematical Monthly , 76 (3): 278–282, doi :10.2307/2316373, JSTOR  2316373, MR  0246207
27. Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016), "El lápiz parabólico: un elemento de línea común", El universo de las cónicas , Springer, pág. 327, doi :10.1007/978-3-662-45450-3, ISBN 978-3-662-45449-7
28. Northshield, Sam (2014), "Teorema del círculo complejo de Descartes", The American Mathematical Monthly , 121 (10): 927–931, doi :10.4169/amer.math.monthly.121.10.927, hdl : 1951/69912 , JSTOR  10.4169/amer.math.monthly.121.10.927, MR  3295667, S2CID  16335704
29. Tupan, Alexandru (2022), "Sobre el teorema del círculo complejo de Descartes", The American Mathematical Monthly , 129 (9): 876–879, doi :10.1080/00029890.2022.2104084, MR  4499753, S2CID  251417228
30. Este es un caso especial de una fórmula para los radios de círculos en una cadena de Steiner con círculos internos y externos concéntricos, dada por Sheydvasser, Arseniy (2023), "3.1 Porismo de Steiner y 3.6 Porismo de Steiner revisitado", Transformaciones fraccionarias lineales , Textos de pregrado en matemáticas, Springer International Publishing, págs. 75–81, 99–101, doi :10.1007/978-3-031-25002-6, ISBN 978-3-031-25001-9, Número de identificación del sujeto  258177153
31. Hajja, Mowaffaq (2009), "93.33 sobre un bocado de Ross Honsberger", The Mathematical Gazette , 93 (527): 309–312, JSTOR  40378744
32. Dergiades, Nikolaos (2007), "Los círculos de Soddy" (PDF) , Forum Geometricorum , 7 : 191–197, MR  2373402
33. Graham, Ronald L. ; Lagarias, Jeffrey C. ; Mallows, Colin L. ; Wilks, Allan R.; Yan, Catherine H. (2003), "Empaquetamientos de círculos apolíneos: teoría de números", Journal of Number Theory , 100 (1): 1–45, arXiv : math/0009113 , doi :10.1016/S0022-314X(03)00015-5, MR  1971245, S2CID  16607718
34. Bradley, Christopher J. (marzo de 2003), "Triángulos de garza y ​​círculos en contacto", The Mathematical Gazette , 87 (508): 36–41, doi :10.1017/s0025557200172080, JSTOR  3620562, S2CID  125024700
35. McGonagle, Annmarie; Northshield, Sam (2014), "Una nueva parametrización de los círculos de Ford", Pi Mu Epsilon Journal , 13 (10): 637–643, JSTOR  24345283, MR  3235834
36. Coxeter, HSM (1968), "Secuencias loxodrómicas de esferas tangentes", Aequationes Mathematicae , 1 (1–2): 104–121, doi :10.1007/BF01817563, MR  0235456, S2CID  119897862
37. Weiss, Asia (1981), "Sobre las secuencias loxodrómicas de esferas tangentes de Coxeter" , en Davis, Chandler; Grünbaum, Branko; Sherk, FA (eds.), La vena geométrica: la Festschrift de Coxeter , Springer, págs. 241–250, doi :10.1007/978-1-4612-5648-9_16, ISBN 978-1-4612-5650-2
38. Lemoine, Émile (1891), "Sur les Triangles orthologiques et sur divers sujets de la géométrie du Triangle" [Sobre triángulos ortológicos y diversos temas de geometría de triángulos], Compte rendu de la 19me session de l'association française pour l' avance de las ciencias, pt. 2 , Congrès de Limoges 1890 (en francés), París: Secrétariat de l'association, págs. 111-146, especialmente §4 "Sur les junctions deux a deux des coniques qui ont pour foyers-deux sommets d'un Triangle et passent par le troisième" [Sobre las intersecciones en pares de las cónicas que tienen como focos dos vértices de un triángulo y pasan por el tercero], págs. 128-144
39. Veldkamp, ​​GR (1985), "El punto isoperimétrico y el punto o puntos de desvío igual en un triángulo", The American Mathematical Monthly , 92 (8): 546–558, doi :10.1080/00029890.1985.11971677, JSTOR  2323159
40. Garcia, Ronaldo; Reznik, Dan; Moses, Peter; Gheorghe, Liliana (2022), "Tríadas de cónicas asociadas a un triángulo", KoG (26), Sociedad Croata de Geometría y Gráficos: 16–32, arXiv : 2112.15232 , doi :10.31896/k.26.2, S2CID  245634505
41. Jackson, Frank M. (2013), "Triángulos soddyianos" (PDF) , Forum Geometricorum , 13 : 1–6
42. Kocik, Jerzy (2007), Un teorema sobre configuraciones circulares , arXiv : 0706.0372
    Kocik, Jerzy (2010), "Ventana dorada" (PDF) , Mathematics Magazine , 83 (5): 384–390, JSTOR  10.4169/002557010x529815, doi :10.4169/002557010x529815

    Kocik, Jerzy (2019), Prueba de la fórmula del círculo de Descartes y su generalización aclarada , arXiv : 1910.09174

43. Coolidge, Julian Lowell (1916), "X. El círculo orientado", Tratado sobre el círculo y la esfera , Clarendon, págs. 351-407, véase también pág. 109, pág. 408
44. Mauldon, JG (1962), "Conjuntos de esferas igualmente inclinadas", Revista canadiense de matemáticas , 14 : 509–516, doi : 10.4153/CJM-1962-042-6
45. Rigby, JF (1981), "La geometría de los ciclos y la inversión generalizada de Laguerre" , en Davis, Chandler; Grünbaum, Branko; Sherk, FA (eds.), The Geometric Vein: The Coxeter Festschrift , Springer, págs. 355–378, doi :10.1007/978-1-4612-5648-9_26, ISBN 978-1-4612-5650-2
46. Se puede encontrar una definición de distancia estereográfica en Li, Hongbo; Hestenes, David; Rockwood, Alyn (2001), "Geometría conforme esférica con álgebra geométrica" ​​(PDF) , Computación geométrica con álgebras de Clifford , Springer, págs. 61–75, CiteSeerX 10.1.1.412.4949 , doi :10.1007/978-3-662-04621-0_3, ISBN  978-3-642-07442-4
47. Este concepto de distancia fue llamado "distancia pseudocordal" para el disco unitario complejo como modelo para el plano hiperbólico por Carathéodory, Constantin (1954) [1950], "§§1.3.86–88 Chordal and Pseudo-chordal Distance", Theory of Functions of a Complex Variable , vol. I, traducido por Steinhardt, Fritz, Chelsea, pp. 81–86, MR  0060009
48. Eriksson, Nicholas; Lagarias, Jeffrey C. (2007), "Empaquetamientos de círculos apolíneos: teoría de números II. Empaquetamientos esféricos e hiperbólicos", The Ramanujan Journal , 14 (3): 437–469, arXiv : math/0403296 , doi :10.1007/s11139-007-9052-6, S2CID  14024662