
La mecánica molecular utiliza la mecánica clásica para modelar sistemas moleculares . Se supone que la aproximación de Born-Oppenheimer es válida y la energía potencial de todos los sistemas se calcula como una función de las coordenadas nucleares utilizando campos de fuerza . La mecánica molecular se puede utilizar para estudiar sistemas de moléculas que varían en tamaño y complejidad desde pequeños a grandes sistemas biológicos o conjuntos de materiales con muchos miles a millones de átomos.
Los métodos de mecánica molecular totalmente atomísticos tienen las siguientes propiedades:
Existen variantes de este tema. Por ejemplo, muchas simulaciones han utilizado históricamente una representación de átomos unidos en la que cada grupo metilo terminal o unidad de metileno intermedia se consideraba una partícula, y los sistemas proteicos grandes se simulan comúnmente utilizando un modelo de microesferas que asigna de dos a cuatro partículas por aminoácido .
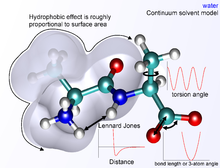
La siguiente abstracción funcional, denominada función potencial interatómica o campo de fuerza en química, calcula la energía potencial del sistema molecular (E) en una conformación dada como una suma de términos de energía individuales.
donde los componentes de las contribuciones covalentes y no covalentes se dan mediante las siguientes sumas:
La forma funcional exacta de la función potencial , o campo de fuerza, depende del programa de simulación particular que se utilice. Generalmente, los términos de enlace y ángulo se modelan como potenciales armónicos centrados alrededor de valores de longitud de enlace de equilibrio derivados de experimentos o cálculos teóricos de la estructura electrónica realizados con software que realiza cálculos de tipo ab-initio como Gaussian . Para una reproducción precisa de los espectros vibracionales, se puede utilizar el potencial de Morse en su lugar, con un costo computacional. Los términos diedros o torsionales suelen tener múltiples mínimos y, por lo tanto, no se pueden modelar como osciladores armónicos, aunque su forma funcional específica varía con la implementación. Esta clase de términos puede incluir términos diedros impropios , que funcionan como factores de corrección para desviaciones fuera del plano (por ejemplo, se pueden utilizar para mantener los anillos de benceno planos o corregir la geometría y la quiralidad de los átomos tetraédricos en una representación de átomos unidos).
Los términos no enlazados son mucho más costosos computacionalmente para calcular en su totalidad, ya que un átomo típico está enlazado a solo unos pocos de sus vecinos, pero interactúa con todos los demás átomos de la molécula. Afortunadamente, el término de van der Waals cae rápidamente. Normalmente se modela utilizando un potencial de Lennard-Jones 6-12 , lo que significa que las fuerzas de atracción caen con la distancia como r −6 y las fuerzas de repulsión como r −12 , donde r representa la distancia entre dos átomos. Sin embargo, la parte repulsiva r −12 no es física, porque la repulsión aumenta exponencialmente. La descripción de las fuerzas de van der Waals por el potencial de Lennard-Jones 6-12 introduce imprecisiones, que se vuelven significativas en distancias cortas. [1] Generalmente se utiliza un radio de corte para acelerar el cálculo de modo que los pares de átomos cuyas distancias sean mayores que el corte tengan una energía de interacción de van der Waals de cero.
Los términos electrostáticos son notoriamente difíciles de calcular bien porque no caen rápidamente con la distancia, y las interacciones electrostáticas de largo alcance son a menudo características importantes del sistema en estudio (especialmente para las proteínas ). La forma funcional básica es el potencial de Coulomb , que solo cae como r −1 . Se utilizan diversos métodos para abordar este problema, siendo el más simple un radio de corte similar al utilizado para los términos de van der Waals. Sin embargo, esto introduce una discontinuidad aguda entre los átomos dentro y fuera del radio. Las funciones de conmutación o escala que modulan la energía electrostática aparente son métodos algo más precisos que multiplican la energía calculada por un factor de escala que varía suavemente de 0 a 1 en los radios de corte externo e interno. Otros métodos más sofisticados pero computacionalmente intensivos son el algoritmo de malla de partículas Ewald (PME) y el algoritmo multipolar .
Además de la forma funcional de cada término de energía, se debe asignar una función de energía útil a los parámetros de las constantes de fuerza, los multiplicadores de van der Waals y otros términos constantes. Estos términos, junto con los valores de enlace, ángulo y diedro de equilibrio, los valores de carga parcial, las masas y radios atómicos y las definiciones de la función de energía, se denominan colectivamente campo de fuerza . La parametrización se realiza normalmente mediante el acuerdo con los valores experimentales y los resultados de los cálculos teóricos. El campo de fuerza de Norman L. Allinger en la última versión de MM4 calcula para los hidrocarburos calores de formación con un error RMS de 0,35 kcal/mol, espectros vibracionales con un error RMS de 24 cm −1 , barreras rotacionales con un error RMS de 2,2°, longitudes de enlace C−C dentro de 0,004 Å y ángulos C−C−C dentro de 1°. [2] Las versiones posteriores de MM4 cubren también compuestos con heteroátomos como las aminas alifáticas. [3]
Cada campo de fuerza está parametrizado para ser internamente consistente, pero los parámetros generalmente no son transferibles de un campo de fuerza a otro.
El principal uso de la mecánica molecular se encuentra en el campo de la dinámica molecular . Esta utiliza el campo de fuerza para calcular las fuerzas que actúan sobre cada partícula y un integrador adecuado para modelar la dinámica de las partículas y predecir trayectorias. Con un muestreo suficiente y sujeto a la hipótesis ergódica , las trayectorias de la dinámica molecular se pueden utilizar para estimar parámetros termodinámicos de un sistema o investigar propiedades cinéticas, como las velocidades y mecanismos de reacción.
La mecánica molecular también se utiliza en la mecánica cuántica y la mecánica molecular , lo que permite el estudio de las proteínas y la cinética enzimática. El sistema se divide en dos regiones: una de las cuales se trata con mecánica cuántica (QM), lo que permite la ruptura y formación de enlaces, y el resto de la proteína se modela utilizando mecánica molecular (MM). La MM por sí sola no permite el estudio de los mecanismos de las enzimas, algo que sí permite la mecánica cuántica. La QM también produce un cálculo energético más exacto del sistema, aunque es mucho más costoso computacionalmente.
Otra aplicación de la mecánica molecular es la minimización de energía, en la que el campo de fuerza se utiliza como criterio de optimización . Este método utiliza un algoritmo apropiado (por ejemplo, el descenso más pronunciado ) para encontrar la estructura molecular de un mínimo de energía local. Estos mínimos corresponden a los confórmeros estables de la molécula (en el campo de fuerza elegido) y el movimiento molecular se puede modelar como vibraciones alrededor e interconversiones entre estos confórmeros estables. Por lo tanto, es común encontrar métodos de minimización de energía local combinados con optimización de energía global, para encontrar el mínimo de energía global (y otros estados de baja energía). A temperatura finita, la molécula pasa la mayor parte de su tiempo en estos estados bajos, que dominan así las propiedades moleculares. La optimización global se puede lograr utilizando recocido simulado , el algoritmo Metropolis y otros métodos de Monte Carlo , o utilizando diferentes métodos deterministas de optimización discreta o continua. Si bien el campo de fuerza representa solo el componente entálpico de la energía libre (y solo este componente se incluye durante la minimización de energía), es posible incluir el componente entrópico mediante el uso de métodos adicionales, como el análisis de modo normal .
Las funciones de energía potencial de la mecánica molecular se han utilizado para calcular constantes de enlace, [4] [5] [6] [7] [8] cinéticas de plegamiento de proteínas, [9] equilibrios de protonación, [10] coordenadas del sitio activo , [6] [11] y para diseñar sitios de enlace . [12]
En mecánica molecular, existen varias formas de definir el entorno que rodea a una molécula o moléculas de interés. Un sistema se puede simular en vacío (denominado simulación en fase gaseosa) sin entorno circundante, pero esto suele ser indeseable porque introduce artefactos en la geometría molecular, especialmente en moléculas cargadas. Las cargas superficiales que normalmente interactuarían con las moléculas de disolvente interactúan entre sí, lo que produce conformaciones moleculares que es poco probable que estén presentes en cualquier otro entorno. La forma más precisa de solvatar un sistema es colocar moléculas de agua explícitas en el cuadro de simulación con las moléculas de interés y tratar las moléculas de agua como partículas interactuantes como las de las otras moléculas. Existe una variedad de modelos de agua con niveles crecientes de complejidad, que representan el agua como una esfera dura simple (un modelo de átomo unido), como tres partículas separadas con un ángulo de enlace fijo, o incluso como cuatro o cinco centros de interacción separados para dar cuenta de los electrones desapareados en el átomo de oxígeno. A medida que los modelos de agua se vuelven más complejos, las simulaciones relacionadas se vuelven más intensivas en términos computacionales. Se ha encontrado un método de compromiso en la solvatación implícita , que reemplaza las moléculas de agua representadas explícitamente con una expresión matemática que reproduce el comportamiento promedio de las moléculas de agua (u otros solventes como los lípidos). Este método es útil para evitar artefactos que surgen de las simulaciones de vacío y reproduce bien las propiedades del solvente en masa, pero no puede reproducir situaciones en las que las moléculas de agua individuales crean interacciones específicas con un soluto que no están bien capturadas por el modelo del solvente, como las moléculas de agua que son parte de la red de enlaces de hidrógeno dentro de una proteína. [13]
Esta es una lista limitada; hay muchos más paquetes disponibles.