.jpg/440px-Tondo_e_quadro_(Bianco,_1436).jpg)
La regla de marteloio es una técnica medieval de cálculo de navegación que utiliza la dirección de la brújula , la distancia y una sencilla tabla trigonométrica conocida como toleta de marteloio . La regla decía a los marineros cómo trazar la travesía entre dos cursos de navegación diferentes mediante la resolución de triángulos con la ayuda de la Toleta y la aritmética básica .
Aquellos que no se sientan cómodos manipulando números podrían recurrir al tondo e quadro visual (círculo y cuadrado) y lograr su respuesta con divisores . La regla de marteloio fue utilizada habitualmente por los navegantes del Mediterráneo durante los siglos XIV y XV, antes del desarrollo de la navegación astronómica .
La etimología proviene de la lengua veneciana . En su atlas de 1436, el capitán y cartógrafo veneciano Andrea Bianco introdujo una tabla de números a la que llamó toleta de marteloio ("tabla de marteloio"), y el método para utilizarla como raxon de marteloio ("razón de marteloio").
El significado de marteloio en sí es incierto. La hipótesis más aceptada, planteada por primera vez por AE Nordenskiöld , es que marteloio se relaciona con " martillo " ("martelo" en veneciano), en referencia al pequeño martillo que se utilizaba para golpear la campana de a bordo del barco para marcar el paso del tiempo. . [1] Se ha sugerido que el sufijo - oio implica que marteloio no significaba exactamente el martillo en sí ni el martillador, sino más bien "el martillazo", con la intención de indicar "el martillazo, el estruendo, el ruido" del cambio de mirar cada cuatro horas. Como había muchos marineros en cubierta durante un cambio de guardia, sería un momento oportuno para que el práctico del barco ordenara un cambio de rumbo (si fuera necesario). [2]
Las hipótesis alternativas (no tan aceptadas) son que "marteloio" es una corrupción de mari logio (que significa "dominio del mar"), [3] o de mare tela (que significa "red marítima"), [4] o que deriva del griego homartologium ( όμαρτόλογίον , que significa "pieza complementaria"), [5] o del griego imeralogium ( ήμερόλογίον , que significa "cálculo diario") [6] o que podría ser del francés del norte matelot , que a su vez proviene del bretón martolod (que significa "marineros"). [7]
.jpg/440px-Medieval_ship_and_compass_(Mandeville).jpg)
La "regla de marteloio" se utilizó en la navegación europea en la Edad Media , sobre todo en el mar Mediterráneo entre los siglos XIV y XVI, aunque puede tener raíces más antiguas. Era una parte integral de la navegación mediante "brújula y carta", antes de la llegada de las coordenadas geográficas y el desarrollo de la navegación celeste en Europa. [8]
La navegación medieval se basaba en dos parámetros: dirección y distancia. A bordo de un barco, la dirección se determinaba mediante la brújula del marinero (que surgió alrededor de 13:00). [9] La distancia se medía a estima ( es decir , distancia = velocidad × tiempo), donde el tiempo se medía con un reloj de media arena y las lecturas de velocidad se tomaban con algún tipo de registro de chip (el método arcaico, utilizado en los siglos XIV y XV, implicaba arrojar un trozo de madera o un pecio por la borda; la tripulación entonaba un canto rítmico para marcar el tiempo que tardaba la astilla en flotar a lo largo del barco). [10]

Trazar un rumbo requería conocer la dirección de la brújula y la distancia entre el punto A y el punto B. Los navegantes adquirían el conocimiento de la ubicación de los puertos entre sí gracias a su larga experiencia en el mar. Esta información en ocasiones era recogida y anotada en un manual de piloto, conocido como portulano ("libro de puerto", en italiano, equivalente al griego periplus , al portugués roteiro y al inglés rutter ). Estos manuales se utilizaron para construir una clase de mapas náuticos conocidos como cartas portulanas . Las cartas portulanas comenzaron a producirse en Génova a finales del siglo XIII y pronto se extendieron a Venecia y Mallorca . Las cartas portulanas no estaban cuadriculadas por líneas de longitud y latitud, sino más bien por una red de líneas de rumbo de brújula , lo que daba a los navegantes una idea sólo de la distancia y dirección entre lugares.

Mediante un manual o una carta portulana, un navegante podría ver inmediatamente que, por ejemplo, Pisa se encontraba a 85 millas al sureste ("Scirocco" en la nomenclatura tradicional de la rosa de los vientos ) de Génova , por lo que un barco que partiera de Génova a Pisa simplemente mantenga ese rumbo durante esa distancia. Sin embargo, la mayoría de los cursos de vela no eran tan buenos. Un marinero que quisiera navegar de Mallorca a Nápoles podría saber que esta última se encontraba a unas 600 millas hacia el este ("Levante"), pero la isla de Cerdeña se encuentra en el camino, por lo que el rumbo del barco debe cambiarse a lo largo de la ruta. Es más fácil decirlo que hacerlo, ya que las coordenadas geográficas no existían durante esta época. La única forma de determinar la posición exacta del barco en el mar sería calcularla mediante el rumbo anterior y la distancia recorrida. [11]
Las islas eran un obstáculo predecible: sortear Cerdeña sería simplemente cuestión de navegar hacia el sureste durante una distancia determinada y luego cambiar el rumbo hacia el noreste ("Greco") durante el resto. Más problemático es si el barco se desviara de su ruta prevista por vientos irregulares o tuviera que virar , cambiando de rumbo repetidamente. ¿Cómo vuelve a su curso previsto? Aquí es donde entró en juego el gobierno de marteloio.
El gobierno de marteloio abordó el problema del cambio de rumbo en el mar. Más específicamente, ayudó al navegante a trazar la travesía de un curso de navegación a otro. [12] Por ejemplo, supongamos que un barco navegase de Córcega a Génova , en dirección norte ("Tramontana") durante unas 130 millas. Pero los vientos no cooperaron y el barco se vio obligado a navegar hacia el noroeste ("Maestro") durante unas 70 millas. ¿Cómo regresa a su ruta original? Reestablecer su rumbo hacia el noreste ("Greco") parece bastante sensato, pero ¿cuánto tiempo debería navegar con ese rumbo? ¿Cómo sabría un navegante cuándo el barco había alcanzado su antigua ruta y debía girar nuevamente hacia el norte? ¿Cómo evitar sobrepasar o no alcanzar el rumbo anterior?

Este es un problema matemático de resolución de un triángulo . Si un navegante sabe cuánto tiempo ha navegado el barco con un rumbo erróneo, puede calcular su distancia actual desde su rumbo previsto y estimar cuánto tiempo debe navegar de regreso con un nuevo rumbo hasta que recupere su rumbo anterior. En el ejemplo de Córcega a Génova, hay un triángulo implícito ACD , con un lado dado ( AC = 70 millas en el rumbo real NW), un ángulo de 45° en A (ángulo de diferencia entre el rumbo real NW y el rumbo previsto N) y otro ángulo de 90° en C (ángulo de diferencia entre el rumbo real NO y el rumbo de regreso NE). El desafío para el navegante es encontrar cuánto tiempo debe navegar en el rumbo de regreso NE (la longitud del lado CD , lo que se llama ritorno ) y cuánto ha avanzado en el rumbo previsto cuando se endereza (la longitud de la hipotenusa AD , o lo que se llama avanzo total ).
Esto es trigonometría elemental , resolviendo dos lados dado un lado (70) y dos ángulos (45° y 90°). Esto se hace rápidamente aplicando la ley de los senos :
arrojando las soluciones ritorno = 70 millas y avanzo total = 98,99 millas. Esto significa que si el barco se orienta al NE desde su posición actual ( C ), alcanzará su rumbo original previsto después de 70 millas de navegación con rumbo NE. Cuando llegue a su punto de unión ( D ), habrá recorrido 98,99 millas de su rumbo original previsto. Allí podrá enderezar su rumbo N y navegar las 30 millas restantes aproximadamente hasta Génova.
Desafortunadamente, los marineros medievales con los niveles educativos rudimentarios de los siglos XIV y XV probablemente no conocían la Ley de Senos ni la manipulaban con facilidad. [13] Como resultado, los navegantes medievales necesitaban un método de cálculo más simple y accesible.
El erudito-clérigo Ramon Llull de Mallorca , fue el primer escritor en hacer referencia a una regla para resolver el problema transversal de la navegación. En su Arbor Scientiae (1295), en el apartado de cuestiones de geometría, Llul escribe:
¿Cómo miden los marineros las millas en el mar ( miliaria in mari )? Los navegantes consideran los cuatro vientos generales, es decir el este, el oeste, el norte y el sur, y también otros cuatro vientos que se encuentran entre ellos, grec (NE), exaloch (SE), lebeg (SW) y maestre (NW). Y miran atentamente el centro del círculo en el que los vientos (rumbos) se encuentran en ángulos; consideran cuando un barco viaja con el viento del este ( levante ) a 100 millas del centro, cuántas millas recorrería con el viento del sureste ( exaloch ); y para 200 millas, duplican el número multiplicando y luego saben cuántas millas hay desde el final de cada 100 millas en dirección este hasta el punto correspondiente en dirección sureste. Y para ello tienen este instrumento [¿una tabla matemática?] y una carta, un cuaderno de ruta, una aguja y la estrella polar." [14]
Lo que Llull parece estar tratando de explicar es que un barco que realmente navega hacia el E, pero con la intención de navegar hacia el SE, puede calcular qué parte de su distancia prevista hacia el sureste ya ha recorrido: lo que los italianos llamaban " avanzar ", pero Lull parece estar tratando de explicar. llamar a la " miliaria in mari ". Llull no explica exactamente cómo, sino que se refiere sólo a un "instrumento", presumiblemente una especie de tabla trigonométrica. Lull implica que los navegantes pueden calcular la miliaria en el rumbo previsto multiplicando la distancia realmente navegada en el rumbo erróneo por el coseno del ángulo entre las dos rutas. [15]

donde θ es el ángulo de diferencia entre las dos rutas.
Usando el ejemplo de Lull, un barco que pretendía navegar hacia el sureste ("Exaloch" en catalán significa "Scirocco") pero en cambio se vio obligado a navegar hacia el este ("Levante"), entonces el ángulo de diferencia es θ = 45°. Después de 100 millas por la ruta errónea, la miliaria en la ruta prevista es 100 × cos 45° = 70,71. Duplicar la navegación en la ruta errónea a 200 millas duplicará la miliaria en la ruta prevista a 141,42 millas (= 200 cos 45°).
(Diagramáticamente, la miliaria in mari de Lull se mide construyendo un triángulo rectángulo pasando una cuerda desde la distancia navegada en el rumbo real hasta el rumbo previsto, encontrándose este último en un ángulo de 90°).
Llull es un poco más explícito en su Ars magna generalis et ultima (escrito hacia 1305). [16] Invirtiendo su ejemplo, con un barco que en realidad navega hacia el sudeste pero tiene la intención de navegar hacia el este, Llull señala que por cada cuatro millas en dirección sureste, "gana tres millas" (2,83 en realidad) en la ruta prevista hacia el este. Así, señala Lull, el barco "pierde 25 millas" (29 en realidad) de su rumbo previsto por cada 100 millas que navega en el rumbo actual.
Nótese que en sus pasajes, Ramon Lull no recomienda la regla, sino que la informa, insinuando que esta regla ya era conocida y utilizada por los marineros contemporáneos en la práctica. [17] Esto quizás no sea sorprendente: aunque la trigonometría estaba apenas en su infancia en la Europa cristiana, las tablas de senos y cosenos ya eran conocidas en las matemáticas árabes . [18] El Reino de Mallorca , bajo dominio musulmán hasta la década de 1230, siguió siendo un centro multicultural en la época de Lull, con florecientes comunidades judías , muchas de las cuales incursionaban en las matemáticas y la astronomía, y cuyos marinos tenían amplios contactos a través del Mar Mediterráneo. [19] No es improbable que los navegantes mallorquines tuvieran a mano algún tipo de tabla trigonométrica. Sin embargo, el contenido exacto y la disposición de esta tabla implícita por Ramon Llull en 1295 son inciertos.
.jpg/440px-Toleta_de_marteloio_(Bianco,_1436).jpg)
Vemos por primera vez la tabla trigonométrica de un marinero más de un siglo después de Llull. En el primer folio de su atlas portulano de 1436 , el capitán veneciano Andrea Bianco explica, en el raxon de marteloio , cómo calcular la travesía y recuperar el rumbo. Presenta una tabla trigonométrica simple a la que llama toleta de marteloio y recomienda que los marineros se la memoricen. [20]
La toleta de marteloio queda redactada de la siguiente manera: [21]
Los números en la Toleta se pueden aproximar mediante las fórmulas modernas: [22]
donde q = número de cuartos de viento (ángulo de diferencia expresado en número de cuartos de viento). Los números funcionan con cuartos de viento establecidos en intervalos de 11,25°, o 11°15', la definición habitual de un cuarto de viento.
La Toleta es una tabla sencilla con varias columnas de números. En la primera columna está el ángulo de diferencia entre el rumbo real y el previsto, expresado en número de cuartos de viento . Una vez que se determina esa diferencia, la segunda columna da el Alargar (el "Ampliación", la distancia actual a la que se encuentra el barco desde el rumbo previsto) mientras que la tercera columna le dice el Avanzar (el "Avance", cuánta distancia hay en el rumbo previsto). El recorrido ya se ha recorrido navegando con el rumbo actual (lo que equivale a la miliaria di mari de Ramon Llull ). Los números de Alargar y Avanzar se muestran en la tabla del Bianco para 100 millas de navegación en el rumbo actual.

Ejemplo : supongamos que un barco pretende navegar hacia el este ("Levante") desde el punto A al punto B. Pero supongamos que los vientos lo obligan a navegar en rumbo sureste por este (SEbE, "Quarto di Scirocco verso Levante"). El sureste por este está a tres cuartos de viento (o 33,75°) del este (en una brújula de 32 puntos , en el orden de los cuartos de viento del este, 1 cuarto es de este a sur, 2 cuartos son de este-sureste) , 3 cuartos es de sureste a este). Eso significa que el navegante deberá consultar la tercera fila, q = 3, de la toleta.
Supongamos que el barco navegó 100 millas con rumbo SE por E. Para verificar su distancia del rumbo previsto hacia el este, el navegante leerá la entrada correspondiente en la columna de alargar e inmediatamente verá que está a 55 millas del rumbo previsto. La columna de avance le informa que habiendo navegado 100 millas en el rumbo actual SEbE, ha recorrido 83 millas del rumbo E previsto.
El siguiente paso es determinar cómo regresar al rumbo previsto. Siguiendo con el ejemplo, para volver al rumbo previsto hacia el este, nuestro marinero tiene que reorientar el rumbo del barco en dirección noreste. Pero hay varios ángulos hacia el noreste: NbE, NNE, NE, ENE, etc. El navegante puede elegir el rumbo: si regresa en un ángulo cerrado (por ejemplo, de norte a este), regresará al rumbo previsto más rápido que en un ángulo cerrado. gradiente más suave (por ejemplo, de este a norte). Cualquiera que sea el ángulo que elija, debe deducir exactamente cuánto tiempo debe navegar en ese rumbo para alcanzar su antiguo rumbo. Si navega demasiado tiempo, corre el riesgo de pasarse.

Calcular el rumbo de regreso es para lo que sirven las últimas tres columnas de la toleta. En la cuarta columna, los ángulos de retorno se expresan como cuartos del rumbo previsto ( no del rumbo actual). En nuestro ejemplo, el marinero tenía la intención de ir hacia el este, pero ha estado navegando de sureste a este durante 100 millas. Dados los vientos, decide que lo mejor es volver al rumbo original reorientando el barco al este-noreste (ENE, "Greco-Levante"). El ENE está dos cuartos de viento por encima del rumbo previsto , Este, por lo que ahora mira la segunda fila ("cuartos = 2") en la cuarta columna de la tabla.
La quinta columna es el ritorno , la distancia que debe recorrer en el ángulo de retorno elegido para recuperar el rumbo original. Dado que ha elegido regresar en rumbo ENE (q = 2), entonces debe leer la segunda fila de la columna de ritorno , que muestra el número 26. Esto representa el número requerido de millas que debe viajar en rumbo ENE por cada 10 millas. se desvió. Recuerde, su alargar (distancia del rumbo previsto) fue de 55 millas. Entonces, para regresar a su rumbo previsto debe recorrer 5,5 × 26 = 143 millas en el ENE. En otras palabras, necesita mantener su rumbo ENE durante 143 millas; una vez recorrida esa distancia, debe enderezar su barco hacia el este y volverá exactamente al rumbo previsto.
La sexta y última columna ( avanzo di ritorno ) indica la longitud del rumbo previsto que ha cumplido en su viaje de regreso. Esto también se expresa en términos de alargar 10 millas. Su alargar fue 55, y su ángulo de retorno fue ENE (por lo tanto q = 2), eso significa que su avanzo di ritorno es 5,5 × 24 = 132. En otras palabras, si todo va bien y nuestro marinero mantiene su rumbo ENE durante 143 millas ( ritorno ), luego, durante ese regreso, habrá cubierto 132 millas adicionales en su rumbo previsto hacia el este ( avanzo di ritorno ).
Finalmente, para calcular la distancia total recorrida (avanzo total) en dirección este durante toda su aventura, debe sumar el avanzar durante la desviación (83 millas) más el avanzo di ritorno (132 millas). Así, en total, ha recorrido 83 + 132 = 215 millas en el recorrido previsto. Al medir esa distancia en el mapa desde el punto de partida ( A ), el navegante puede determinar su posición actual exacta.
Este es el uso más sencillo de la toleta de marteloio. Es, en esencia, una tabla trigonométrica. Sin embargo, no aborda el problema transversal de una sola vez, como la Ley de los Senos, sino que divide el problema en dos triángulos rectángulos que procede a resolver sucesivamente. La trigonometría moderna prescindiría del paso de calcular el alargar y calcularía el ritorno directamente, pero para eso es necesario estar armado con una tabla de senos completa . La toleta es una tabla bastante sencilla, fácil de consultar y realizar cálculos, y lo suficientemente compacta para ser memorizada por los navegantes (como recomienda Bianco).
La toleta de marteloio se expresa con bonitos números redondos, 100 y 10. Pero, en la práctica, un barco normalmente no navegaría 100 millas antes de intentar regresar, sino alguna otra distancia, digamos 65 millas. Calcular esto es un problema simple de resolución de razones . Por ejemplo, si el barco había navegado 65 millas de sureste a este, entonces calcular el alargar del rumbo previsto hacia el este es simplemente una cuestión de resolver lo siguiente para x :
donde 55 es el alargar por 100 millas (como se indica en la segunda columna de la tabla en q = 3). Esto se hace fácilmente mediante la simple " Regla de Tres ", un método de multiplicación cruzada, que utiliza tres números para resolver el cuarto mediante multiplicación y división sucesivas:
Entonces, navegar 65 millas por el SE por E implica alargar = x = 35,75 millas. El avanzar, etc. se puede calcular de manera análoga.
Si bien la "regla de tres" ya se conocía en el siglo XIV, la habilidad para ejecutar la multiplicación y la división podía resultar difícil de alcanzar para los marineros medievales procedentes de una sociedad mayoritariamente analfabeta. Sin embargo, no era inaccesible. Como insta Andrea Bianco, los navegantes deben "saber multiplicar bien y dividir bien" ("saver ben moltiplichar e ben partir") [23] Es aquí donde vemos la importante interfaz entre el comercio y la navegación. Las matemáticas del comercio ( números arábigos , multiplicación, división, fracciones , las herramientas necesarias para calcular las compras y ventas de bienes y otras transacciones comerciales) eran esencialmente las mismas que las matemáticas de la navegación. [24] Y este tipo de matemáticas se enseñaba en las escuelas de ábaco que se establecieron en el siglo XIII en los centros comerciales del norte de Italia para formar a los hijos de los comerciantes, la misma clase de la que procedían los navegantes italianos. Como señala el historiador EGR Taylor, "los marineros fueron el primer grupo profesional en utilizar las matemáticas en su trabajo diario" [25]
.jpg/440px-Tondo_e_quadro_(basic_features).jpg)
Para aquellos preocupados por el elevado arte de manipular números, había una alternativa. Este fue el recurso visual conocido como "círculo y cuadrado" ( tondo e quadro ), también proporcionado por Andrea Bianco en su atlas de 1436. [26]
El círculo era una rosa de los vientos de 32 vientos (o conjunto de líneas de rumbo). El círculo estaba inscrito con una cuadrícula de 8 × 8.
La rosa de los vientos en el centro puede pasarse por alto; de hecho, el círculo en sí puede ignorarse, ya que parece no tener otro propósito que la construcción de los rayos que atraviesan la cuadrícula. [27] La rosa de interés está en la esquina superior izquierda de la cuadrícula. Desde esa esquina, emanan una serie de líneas de rumbo de brújula . En su tondo e quadro original de 1436 , Bianco tiene dieciséis rayos emanantes, es decir, Bianco incluye medio cuarto de viento u octavo viento ( otava ), de modo que los rayos que emanan están a intervalos de 5,625 grados. Otras construcciones del círculo y el cuadrado, por ejemplo el Atlas Cornaro , utilizan sólo ocho rayos que emanan a una distancia de un cuarto de viento (11,25 grados). Visualmente, estos rayos replican el cuarto inferior derecho de una rosa de los vientos de 32 vientos : Este (0q), E por S (1q), ESE (2q), SE por E (3q), SE (4q), SE por S ( 5q), SSE (6q), S por E (7q) y Sur (8q).

Encima de la cuadrícula hay una escala de barra de distancia , con muescas con subunidades. Hay dos conjuntos de números en la escala, uno para medir cada cuadrado de cuadrícula por 20 millas, otro para medir cada cuadrado de cuadrícula por 100 millas (ver diagrama). [28] La barra superior es la escala de 20 m por cuadrado, y cada punto negro indica una milla. La barra inferior es la escala de 100 m por cuadrado, donde la longitud de un cuadrado unitario se divide en dos subcuadrados iguales de 50 m, y un conjunto de puntos y líneas rojas lo dividen en longitudes de 10 millas. Entonces, dependiendo de la escala que se elija, la longitud del lado de toda la cuadrícula (ocho cuadrados) podría medirse hasta 160 millas (usando la escala de 20 m por cuadrado) o hasta 800 millas (usando la escala de 100 m por cuadrado). -escala cuadrada).
.jpg/440px-Tondo_e_quadro_detail_(Bianco,_1436).jpg)
El querubín con los divisores sugiere cómo se supone que un navegante debe usar la cuadrícula para calcular alargar y avanzar mediante medición visual en lugar de manipular números.
.jpg/440px-Tondo_e_quadro_(calculation).jpg)
Ejemplo : supongamos que el barco ha viajado 120 millas con dos cuartos de viento por debajo del rumbo previsto (por ejemplo, viajó al ESE, cuando el rumbo previsto es Este). Utilizando los divisores y la escala de 20 m, el navegante puede medir 120 millas con sus divisores. Luego, colocando un extremo en la esquina superior izquierda ( A ), coloca los divisores a lo largo del rayo ESE (= dos cuartos de viento debajo del rayo Este, o la parte superior horizontal de la cuadrícula) y marca el punto (punto B en el diagrama). ). Luego , usando una regla , dibuja una línea hasta el rayo Este y marca el punto correspondiente C.
Es fácil ver inmediatamente que se ha creado un triángulo rectángulo ABC . La longitud BC es el alargar (distancia desde el rumbo previsto), que se puede medir como 46 millas (esto se puede ver visualmente como dos cuadrados más un bit, es decir, 20 m + 20 m y un bit que se puede evaluar como 6 m por utilizando los divisores y la báscula de barra de 20 m). La longitud AC es el avance (distancia compensada), que es 111 millas; visualmente, cinco cuadrados y un poco, o (20 × 5) + 11, medido nuevamente con divisores y escala.
Así es como el "círculo y cuadrado" evita manipular los números mediante la multiplicación y la división o la regla de tres. El navegante puede evaluar el avance y alargar visualmente, únicamente mediante medición.
Este método se puede utilizar para cualquier rumbo y desviación previstos, ya que el único propósito es resolver el triángulo mediante divisores y escala. por ejemplo, utilizando nuestro primer ejemplo de Córcega a Génova, donde el rumbo previsto era Norte pero el barco en realidad navegaba Noroeste, el navegante colocaría los divisores a una longitud de 70 millas y los colocaría a lo largo del cuarto cuarto de viento (= rayo SE en el tondo e quadro , ya que el NO está a cuatro cuartos de viento del Norte). Calcularía alargar y avanzar exactamente de la misma manera: dibujaría una línea hasta la parte superior horizontal de la cuadrícula, mediría los cuadrados, etc.
El dispositivo tondo e quadro es muy similar al cuadrante sinusoidal árabe ( Rubul mujayyab ), con los rayos de las esquinas replicando el papel de la plomada ajustable . [29]
Si bien la toleta de marteloio (y su contraparte visual, el tondo e quadro ) están diseñadas para la tarea explícita de recuperar un rumbo previsto, se pueden usar de más maneras, para muchas clases de problemas de navegación, por ejemplo, trazar un rumbo con múltiples -cambios de rodamientos, etc. [30]
Una de las aplicaciones interesantes de la regla de marteloio es la triangulación , por ejemplo, determinando la distancia del barco desde un punto de referencia en la costa. (Este fue el último ejercicio intentado en el cuaderno del navegante veneciano Miguel de Rodas, que replicamos aquí.) [31]
Ejemplo : supongamos que un barco que navega al NO ("Maestro") ve un punto de referencia hacia el oeste ("Ponente") una noche, pero se desconoce la distancia. Supongamos que el barco continúa navegando en la ruta NO durante la noche y a la mañana siguiente, 40 millas más tarde, nota que el punto de referencia ahora está al oeste-suroeste (WSW, "Ponente-Libeccio") de su posición actual. Encontrar la distancia entre el punto de referencia y el barco es solo una aplicación de la regla de marteloio.

Para resolver el problema, comience desde la posición nocturna ( A en el mapa) y trate la distancia entre el barco y el punto de referencia (longitud AB ) como el rumbo previsto y la ruta real del barco (NW) como una desviación. Calcular la distancia del punto de referencia desde la posición del barco en la mañana ( C ) es cuestión de tratar la distancia BC como el ritorno calculado. Como necesitamos saber el alargar para calcular el ritorno, este es un procedimiento de dos pasos.
Primero, observe que el NO está cuatro cuartos de viento por encima del W, por lo que mirando hacia arriba en la toleta , en la fila q = 4, el alargar es 71 millas por cada 100 millas en el rumbo NO. Pero el barco solo navegó 40 millas durante la noche, por lo que tenemos que resolver la razón 71/100 = x /40, que por la regla de tres significa x = alargar = 28,4 millas. En otras palabras, al navegar durante la noche al NO por 40 millas de A a C, el barco ahora está a 28,4 millas de su rumbo "previsto" hacia el oeste.
Ahora el ritorno. El punto de referencia, como se señaló, está al WSW de la posición matutina del barco ( C ). Entonces, para "regresar" al punto de referencia, el barco debe cambiar su rumbo de su rumbo NO actual a un rumbo WSW, es decir, 6 cuartos de viento por debajo del NO. Sin embargo, la toleta especifica los cuartos de viento en términos de la dirección "pretendida" (en este caso, Oeste), y el WSW son dos cuartos de viento por debajo del Oeste, por lo que debemos observar la fila q = 2. Esto significa que el ritorno es de 26 millas por cada 10 millas alargar. Como el alargar es 28,4, eso significa que el ritorno es 26 × 2,84 = 73,84. Y ahí lo tenemos. El punto de referencia está a 73,84 millas de la posición matutina del barco.
(Para completar la historia, es posible que deseemos averiguar la distancia a la que se encontraba ese punto de referencia la noche anterior (es decir, desde el punto A hasta el punto de referencia B). Eso es simplemente cuestión de sumar avanzar y avanzo in ritorno. Los cálculos rápidos muestran el avance (@ q = 4, para 40 millas) es 28,4 millas (= 71 × 40/100) y el avanzo di ritorno (@ q = 2 para 28,4 millas alargar), es 2,84 × 24 = 68,16 Entonces total avanzo = 28,4 +. 68,16 = 96,56 millas. Esa era la distancia entre el punto de referencia y el barco la noche anterior).
La regla de marteloio también puede utilizarse con el avance como objetivo, por ejemplo, supongamos que un barco parte con la intención de encontrar la Línea Tordesillas , el meridiano legalmente fijado en un tratado de 1494 a 370 leguas al oeste de Cabo Verde . El barco no necesitaba partir de Cabo Verde y navegar constantemente con rumbo Oeste para encontrarlo. Más bien, puede navegar con un rumbo más conveniente (por ejemplo, SO) y tratar al Oeste como un rumbo "previsto". Así, utilizando la regla marteloio, puede seguir navegando hasta que el avance en el rumbo "previsto" Oeste alcance las 370 leguas.
De hecho, ni siquiera necesita salir de Cabo Verde, sino que puede partir de otro lugar, digamos, Sevilla , y utilizar la distancia y el rumbo conocidos de Cabo Verde (es decir, Sevilla) y la regla de marteloio para calcular cuándo finalmente ha llegado. Llegamos al meridiano de Tordesillas. Esto requiere un par de pasos. Supongamos que Cabo Verde ( B en el mapa) está a 400 leguas al suroeste de Sevilla ( A en el mapa), pero el barco pretende ir directamente al Oeste desde Sevilla para llegar al meridiano de Tordesillas en mar abierto. ¿Cuánto tiempo necesita navegar?

La forma de resolver esto mediante la regla de marteloio es plantear el problema a la inversa: tratar al oeste como el rumbo previsto y al suroeste como el rumbo real. El SW está cuatro cuartos de viento por debajo del W, por lo que mirando hacia arriba en la toleta q = 4, el avance es 71 por cada 100 millas navegadas. Entonces, si un barco navegó 400 leguas en el rumbo SO "real" hacia Cabo Verde, lograría un avance de 284 leguas (= 71 × 4) en el rumbo "previsto" hacia el Oeste. Por supuesto, el barco en realidad no navega hacia el SO hacia Cabo Verde, sino hacia el O hacia mar abierto. En otras palabras, cuando el barco zarpa hacia el Oeste desde Sevilla, sabe que necesita navegar 284 leguas hacia el Oeste antes de llegar al meridiano implícito de Cabo Verde (punto C en el mapa), y sólo debe empezar a contar las 370 leguas hacia el Oeste. Línea Tordesillas a partir de entonces. Es decir, necesita navegar un total de 284 + 370 = 654 leguas al Oeste de Sevilla para llegar a la línea de Tordesillas (punto D del mapa).
Si bien este ejemplo particular muestra la flexibilidad de la regla de marteloio, también muestra uno de sus principales inconvenientes: el resultado ignora por completo la curvatura de la Tierra , es decir, el hecho de que las líneas de los meridianos de longitud convergen en el Polo Norte y, por lo tanto, se estrechan en latitudes más altas. Contra lo que sugiere el marteloio, 370 leguas al oeste de Cabo Verde no están en el mismo meridiano de longitud que 654 leguas al oeste de Sevilla. Debido a que Sevilla está muy al norte de Cabo Verde, los meridianos están agrupados más juntos en la latitud de Sevilla que en la latitud de Cabo Verde. De hecho, un barco que navegue al oeste de Sevilla llegará al verdadero meridiano de Tordesillas (punto T del mapa) mucho antes de navegar 654 leguas (punto D ).
La regla de marteloio hace que los marineros tracen rutas dibujando triángulos planos en una carta, como si la superficie del mundo fuera plana. Si bien esto podría ser bastante práctico para navegar confinado a las latitudes compactas del Mar Mediterráneo , es bastante engañoso a mayor escala.
A finales del siglo XV y XVI, la mejora de la astronomía náutica y la introducción de paralelos de latitud permitieron a los navegantes determinar su posición en el mar mediante lecturas celestes, en lugar de depender de la estimación de la distancia navegada. [32] El sucesor del gobierno de marteloio fue el "Regimiento de las Ligas" ( regimiento das léguas ), que fue utilizado por los navegantes portugueses que navegaban en el Océano Atlántico. O, para utilizar el término introducido por William Bourne (1571), la "Regla para elevar o colocar un título", también conocida como "Tabla de ligas" o "Regla para elevar el polo". [33] Fue escrito por primera vez en el manual de navegación portugués Regimento do astrolabio e do quadrante (publicado en Lisboa c. 1509, pero escrito c. 1480) [34] Fue popularizado por Martín Cortés de Albacar en su Breve compendio la de 1551. esfera y del arte de navegar .
El "Regimiento de las Ligas" no es muy diferente del gobierno de marteloio. El Regimiento de las Ligas siempre considera el rumbo oeste-este como el "rumbo previsto" y mide las desviaciones establecidas del mismo. Más específicamente, la tabla de clasificación considera un valor fijo de alargar – fijado en 1 grado de latitud (o, en las mediciones de la época, 17,5 leguas (portuguesas) , o equivalentemente 70 millas (italianas) ). [35] Luego proporciona para cada cuarto de viento diferente de la dirección de navegación (siempre designado como cuartos de distancia del eje norte-sur, en lugar de lejos del rumbo previsto), el relevar y el afastar . El relevar es el número de leguas del rumbo real que debe navegar un barco para recorrer el grado de latitud preestablecido (17,5 leguas de alargar del paralelo inicial). El afastar es simplemente el correspondiente avanzar en dirección oeste-este.
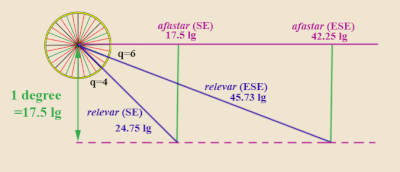
Ejemplo : supongamos que un barco zarpa con rumbo este-sureste (ESE). Es decir, seis cuartos de viento por encima del Sur (recuerde: a diferencia del marteloio, el Regimiento de las Ligas siempre mide cuartos de viento lejos del meridiano norte-sur). Mirando cualquier regimiento de la tabla de ligas (por ejemplo, Martín Cortés de Albacar , 1551), [36] para q = 6, la tabla da el relevar como 45 11 ⁄ 15 leguas y el afastar como 42 1 ⁄ 4 leguas. Esto significa que un barco que navegue por el rumbo ESE tendrá que navegar 45,73 leguas para recorrer un grado de latitud (17,5 leguas de alargar del rumbo este, para usar la lengua marteloio), y el correspondiente afastar ( avance en términos marteloio) serán 42,25 leguas.
Si, en cambio, el barco hubiera zarpado con rumbo SE, es decir cuatro cuartos de viento sobre el Sur, los valores correspondientes de la tabla del Regimiento de Ligas en q = 4 son relevar = 24 3 ⁄ 4 y afastar = 17 1 ⁄ 2 .
Observe que el rumbo SE alcanza el alargar 1 grado más rápido (es decir, un relevar más pequeño ) que el rumbo ESE, y tendrá menos afastar (más cerca del meridiano N-S).
Matemáticamente,
donde θ = 11,25 × número de cuartos de viento alejados del eje norte-sur.
A pesar de la diferencia de terminología, en particular el uso de grados de latitud, la regla de marteloio y el Regimiento de las Ligas son muy similares: ambos tratan de resolver triángulos en una carta plana. La ventaja del regimiento sobre el marteloio es la introducción de paralelos de latitud en la tabla, de modo que la posición puede comprobarse mediante observación astronómica (vía cuadrante , astrolabio , etc.), y no tener que depender totalmente de las estimaciones de distancia y de los marineros. dirección.
Con el regimiento, las coordenadas geográficas también se pueden utilizar para guiar la navegación. Por ejemplo, la búsqueda de la línea de Todesillas (meridiano a 370 leguas al oeste de Cabo Verde) se simplifica mucho con referencia a una latitud precisa. Por ejemplo, supongamos que dos barcos salen de Cabo Verde (17° N), uno con rumbo oeste por norte (WbN, es decir, un cuarto por encima del oeste, o q = 7 desde el eje norte), y el otro con rumbo oeste-noroeste. (WNW, dos cuartos arriba del oeste, o q = 6 desde el eje Norte). Utilizando el Regimiento de las Ligas, es posible calcular las latitudes precisas en las que cruzarán el meridiano de Tordesillas; basta con dividir 370 leguas al oeste por el afastar implícito en las diferentes direcciones. El barco WbN alcanzará el meridiano cuando alcance la latitud 21° 21' N, mientras que el barco WNW lo alcanzará cuando alcance la latitud 29° N. [37] Entonces, en lugar de contar leguas con lecturas de reloj de arena y velocidad, los barcos pueden simplemente mantener el rumbo y realizar observaciones astronómicas periódicas para evaluar su latitud.
La toleta de marteloio es ancestral de la moderna "mesa transversal" utilizada en la navegación más moderna. [38] En la nomenclatura moderna, la travesía es el "camino torcido que hace un barco cuando navega en varias direcciones sucesivas" y resolver la travesía es "el método de encontrar un solo rumbo y distancia que llevaría a un barco al mismo lugar como dos o más cursos y distancias". [39] En lenguaje marteloio, al "resolver la travesía", la información conocida que se da es el "rumbo real" y el "ritorno", mientras que las incógnitas son el "rumbo previsto" y el "avanzo total".
Las tablas de recorrido utilizan tres valores para cada uno de los segmentos del rumbo torcido: la distancia (Dist.), la diferencia de latitud (D.Lat., movimiento a lo largo del eje N-S) y la salida (Dep., movimiento a lo largo del eje E-W). , los dos últimos calculados mediante las fórmulas:
donde θ es la diferencia angular del rumbo desde el eje N–S si los valores de θ son inferiores a 45°; Sin embargo, si el ángulo excede los 45°, entonces θ se expresa como el ángulo de diferencia desde el eje E-O, y las fórmulas se invierten, es decir, la fórmula de Diferencia de Latitud se convierte en la Salida, y la fórmula de Salida es la Diferencia de Latitud). O, aún más simplemente, calcule θ como el ángulo de diferencia desde el viento principal más cercano (N, S, E, W), ejecute las fórmulas y luego coloque el número mayor en la columna apropiada (D.Lat. o Dep.) .
Para cada segmento de rumbo, el navegador inserta el trío relevante (Dist., D.Lat., Dep.) y puede calcular el rumbo implícito desde el principio hasta el punto final y la distancia cumplida en ese rumbo. Luego combina, mediante suma y resta, todas las diferencias de latitud y salida, para obtener la diferencia general de latitud y salida, y la convierte nuevamente en rumbo y distancia generales corregidos. [40]
Dejando a un lado las sugerentes observaciones de Ramon Llull de 1295, la primera referencia conocida a marteloio data de 1390, en el inventario de la finca de la madre de un tal Oberto Foglieto de Génova, donde una entrada dice unum martelogium....item carta una pro navegando . [41] La primera aparición y explicación clara es el atlas de 1436 del capitán veneciano Andrea Bianco . Desde entonces se han encontrado otros manuscritos antiguos que relacionan el gobierno de marteloio, entre ellos: [42]
.jpg/440px-Toleta_de_marteloio_(Cornaro_Atlas).jpg)