La ruptura espontánea de simetría es un proceso espontáneo de ruptura de simetría , por el cual un sistema físico en un estado simétrico termina espontáneamente en un estado asimétrico. [1] [2] [3] En particular, puede describir sistemas donde las ecuaciones de movimiento o el lagrangiano obedecen a simetrías, pero las soluciones de vacío de menor energía no exhiben esa misma simetría . Cuando el sistema pasa a una de esas soluciones de vacío, la simetría se rompe para las perturbaciones alrededor de ese vacío aunque el lagrangiano entero retiene esa simetría.
La ruptura espontánea de la simetría no puede ocurrir en la mecánica cuántica que describe sistemas de dimensión finita, debido al teorema de Stone-von Neumann (que establece la unicidad de las relaciones de conmutación de Heisenberg en dimensiones finitas). Por lo tanto, la ruptura espontánea de la simetría solo puede observarse en teorías de dimensión infinita, como las teorías cuánticas de campos .
Por definición, la ruptura espontánea de la simetría requiere la existencia de leyes físicas que sean invariantes ante una transformación de simetría (como la traslación o la rotación), de modo que cualquier par de resultados que difiera solo en esa transformación tenga la misma distribución de probabilidad. Por ejemplo, si las mediciones de un observable en dos posiciones diferentes tienen la misma distribución de probabilidad, el observable tiene simetría traslacional.
La ruptura espontánea de la simetría ocurre cuando esta relación se rompe, mientras que las leyes físicas subyacentes permanecen simétricas.
Por el contrario, en la ruptura explícita de la simetría , si se consideran dos resultados, las distribuciones de probabilidad de un par de resultados pueden ser diferentes. Por ejemplo, en un campo eléctrico, las fuerzas sobre una partícula cargada son diferentes en distintas direcciones, por lo que la simetría rotacional se rompe explícitamente por el campo eléctrico que no tiene esta simetría.
Las fases de la materia, como los cristales, los imanes y los superconductores convencionales, así como las transiciones de fase simples , pueden describirse mediante la ruptura espontánea de la simetría. Entre las excepciones notables se incluyen las fases topológicas de la materia, como el efecto Hall cuántico fraccionario .
Por lo general, cuando se produce una ruptura espontánea de la simetría, las propiedades observables del sistema cambian de múltiples maneras. Por ejemplo, se espera que la densidad, la compresibilidad, el coeficiente de expansión térmica y el calor específico cambien cuando un líquido se convierte en sólido.
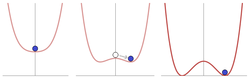
Consideremos una cúpula simétrica hacia arriba con un canal que rodea la base. Si se coloca una pelota en la cúspide de la cúpula, el sistema es simétrico con respecto a una rotación alrededor del eje central. Pero la pelota puede romper espontáneamente esta simetría al rodar por la cúpula hacia el canal, un punto de menor energía. Después, la pelota se detiene en algún punto fijo del perímetro. La cúpula y la pelota conservan su simetría individual, pero el sistema no. [4]
En el modelo relativista idealizado más simple, la simetría rota espontáneamente se resume a través de una teoría de campo escalar ilustrativa . El lagrangiano relevante de un campo escalar , que esencialmente dicta cómo se comporta un sistema, se puede dividir en términos cinéticos y potenciales.
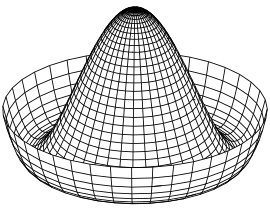
Es en este término potencial donde se produce la ruptura de simetría. En el gráfico de la izquierda se ilustra un ejemplo de potencial, creado por Jeffrey Goldstone [5] .
Este potencial tiene un número infinito de mínimos posibles (estados de vacío) dados por
para cualquier θ real entre 0 y 2 π . El sistema también tiene un estado de vacío inestable correspondiente a Φ = 0 . Este estado tiene una simetría U(1) . Sin embargo, una vez que el sistema cae en un estado de vacío estable específico (que equivale a una elección de θ ), esta simetría parecerá perderse o "romperse espontáneamente".
De hecho, cualquier otra elección de θ tendría exactamente la misma energía, y las ecuaciones definitorias respetan la simetría, pero el estado fundamental (vacío) de la teoría rompe la simetría, lo que implica la existencia de un bosón de Nambu-Goldstone sin masa , el modo que gira alrededor del círculo en el mínimo de este potencial, e indica que hay algún recuerdo de la simetría original en el lagrangiano. [6] [7]
En física de partículas , las partículas portadoras de fuerza se especifican normalmente mediante ecuaciones de campo con simetría de calibre ; sus ecuaciones predicen que ciertas mediciones serán las mismas en cualquier punto del campo. Por ejemplo, las ecuaciones de campo podrían predecir que la masa de dos quarks es constante. Resolver las ecuaciones para encontrar la masa de cada quark podría dar dos soluciones. En una solución, el quark A es más pesado que el quark B. En la segunda solución, el quark B es más pesado que el quark A en la misma cantidad . La simetría de las ecuaciones no se refleja en las soluciones individuales, pero sí en el rango de soluciones.
Una medición real refleja solo una solución, lo que representa una ruptura en la simetría de la teoría subyacente. "Oculto" es un término mejor que "roto", porque la simetría siempre está presente en estas ecuaciones. Este fenómeno se llama ruptura espontánea de simetría (SSB) porque nada (que sepamos) rompe la simetría en las ecuaciones. [8] : 194–195 Por la naturaleza de la ruptura espontánea de simetría, diferentes porciones del Universo primitivo romperían la simetría en diferentes direcciones, lo que llevaría a defectos topológicos , como paredes de dominio bidimensionales , cuerdas cósmicas unidimensionales , monopolos de dimensión cero y/o texturas , dependiendo del grupo de homotopía relevante y la dinámica de la teoría. Por ejemplo, la ruptura de la simetría de Higgs puede haber creado cuerdas cósmicas primordiales como subproducto. La ruptura hipotética de la simetría GUT produce genéricamente monopolos , lo que crea dificultades para GUT a menos que los monopolos (junto con cualquier pared del dominio GUT) sean expulsados de nuestro Universo observable a través de la inflación cósmica . [9]
La ruptura de la simetría quiral es un ejemplo de ruptura espontánea de la simetría que afecta a la simetría quiral de las interacciones fuertes en la física de partículas. Es una propiedad de la cromodinámica cuántica , la teoría cuántica de campos que describe estas interacciones, y es responsable de la mayor parte de la masa (más del 99 %) de los nucleones y, por lo tanto, de toda la materia común, ya que convierte quarks muy ligeros ligados en constituyentes 100 veces más pesados de los bariones . Los bosones de Nambu-Goldstone aproximados en este proceso de ruptura espontánea de la simetría son los piones , cuya masa es un orden de magnitud más ligera que la masa de los nucleones. Sirvió como prototipo e ingrediente significativo del mecanismo de Higgs que subyace a la ruptura de la simetría electrodébil.
Las fuerzas fuerte, débil y electromagnética pueden entenderse como derivadas de simetrías de calibre , lo que es una redundancia en la descripción de la simetría. El mecanismo de Higgs , la ruptura espontánea de la simetría de las simetrías de calibre, es un componente importante para entender la superconductividad de los metales y el origen de las masas de las partículas en el modelo estándar de la física de partículas. El término "ruptura espontánea de la simetría" es un nombre inapropiado aquí, ya que el teorema de Elitzur establece que las simetrías de calibre locales nunca pueden romperse espontáneamente. Más bien, después de la fijación de calibre, la simetría global (o redundancia) puede romperse de una manera formalmente similar a la ruptura espontánea de la simetría. Una consecuencia importante de la distinción entre simetrías verdaderas y simetrías de calibre es que las Nambu-Goldstone sin masa resultantes de la ruptura espontánea de una simetría de calibre se absorben en la descripción del campo vectorial de calibre, lo que proporciona modos de campo vectorial masivos, como el modo de plasma en un superconductor o el modo de Higgs observado en la física de partículas.
En el modelo estándar de física de partículas, la ruptura espontánea de la simetría de calibración SU(2) × U(1) asociada con la fuerza electrodébil genera masas para varias partículas y separa las fuerzas electromagnética y débil. Los bosones W y Z son las partículas elementales que median la interacción débil , mientras que el fotón media la interacción electromagnética . A energías mucho mayores que 100 GeV, todas estas partículas se comportan de manera similar. La teoría de Weinberg-Salam predice que, a energías más bajas, esta simetría se rompe de modo que emergen el fotón y los bosones masivos W y Z. [10] Además, los fermiones desarrollan masa de manera consistente.
Sin la ruptura espontánea de la simetría, el Modelo Estándar de interacciones entre partículas elementales requiere la existencia de un cierto número de partículas. Sin embargo, se podría predecir que algunas partículas (los bosones W y Z ) carecerían de masa, cuando en realidad se observa que sí la tienen. Para superar esto, la ruptura espontánea de la simetría se ve aumentada por el mecanismo de Higgs para otorgar masa a estas partículas. También sugiere la presencia de una nueva partícula, el bosón de Higgs , detectado en 2012.
La superconductividad de los metales es un análogo de la materia condensada del fenómeno de Higgs, en el que un condensado de pares de electrones de Cooper rompe espontáneamente la simetría de calibre U(1) asociada con la luz y el electromagnetismo.
La ruptura de simetría dinámica (DSB) es una forma especial de ruptura de simetría espontánea en la que el estado fundamental del sistema tiene propiedades de simetría reducidas en comparación con su descripción teórica (es decir, lagrangiana ).
La ruptura dinámica de una simetría global es una ruptura espontánea de la simetría, que no ocurre en el nivel del árbol (clásico) (es decir, en el nivel de la acción pura), sino debido a correcciones cuánticas (es decir, en el nivel de la acción efectiva ).
La ruptura dinámica de una simetría de norma es más sutil. En la ruptura espontánea convencional de la simetría de norma, existe una partícula de Higgs inestable en la teoría, que lleva al vacío a una fase de ruptura de simetría (es decir, interacciones electrodébiles ). Sin embargo, en la ruptura dinámica de la simetría de norma, no opera ninguna partícula de Higgs inestable en la teoría, sino que los estados ligados del propio sistema proporcionan los campos inestables que generan la transición de fase. Por ejemplo, Bardeen, Hill y Lindner publicaron un artículo que intenta reemplazar el mecanismo de Higgs convencional en el modelo estándar por un DSB que es impulsado por un estado ligado de quarks top-antitop. (Estos modelos, en los que una partícula compuesta desempeña el papel del bosón de Higgs, a menudo se denominan "modelos de Higgs compuestos"). [11] La ruptura dinámica de las simetrías de calibre se debe a menudo a la creación de un condensado fermiónico , por ejemplo, el condensado de quarks , que está conectado a la ruptura dinámica de la simetría quiral en la cromodinámica cuántica . La superconductividad convencional es el ejemplo paradigmático desde el lado de la materia condensada, donde las atracciones mediadas por fonones llevan a los electrones a unirse en pares y luego condensarse, rompiendo así la simetría de calibre electromagnética.
La mayoría de las fases de la materia pueden entenderse a través de la lente de la ruptura espontánea de la simetría. Por ejemplo, los cristales son conjuntos periódicos de átomos que no son invariantes bajo todas las traslaciones (solo bajo un pequeño subconjunto de traslaciones por un vector reticular). Los imanes tienen polos norte y sur que están orientados en una dirección específica, rompiendo la simetría rotacional . Además de estos ejemplos, hay toda una serie de otras fases de la materia que rompen la simetría, incluidas las fases nemáticas de los cristales líquidos , las ondas de densidad de carga y espín, los superfluidos y muchas otras.
Existen varios ejemplos conocidos de materia que no pueden describirse mediante la ruptura espontánea de la simetría, entre ellos: fases de materia ordenadas topológicamente, como los líquidos Hall cuánticos fraccionarios y los líquidos de espín . Estos estados no rompen ninguna simetría, sino que son fases distintas de la materia. A diferencia del caso de la ruptura espontánea de la simetría, no existe un marco general para describir dichos estados. [12]
El ferroimán es el sistema canónico que rompe espontáneamente la simetría continua de los espines por debajo de la temperatura de Curie y en h = 0 , donde h es el campo magnético externo. Por debajo de la temperatura de Curie , la energía del sistema es invariante bajo la inversión de la magnetización m ( x ) tal que m ( x ) = − m (− x ) . La simetría se rompe espontáneamente cuando h → 0 cuando el hamiltoniano se vuelve invariante bajo la transformación de inversión, pero el valor esperado no es invariante.
Las fases de la materia que rompen espontáneamente la simetría se caracterizan por un parámetro de orden que describe la cantidad que rompe la simetría considerada. Por ejemplo, en un imán, el parámetro de orden es la magnetización local.
La ruptura espontánea de una simetría continua está acompañada inevitablemente por modos Nambu-Goldstone sin gapless (lo que significa que estos modos no requieren ningún gasto de energía para excitarse) asociados con fluctuaciones lentas y de longitud de onda larga del parámetro de orden. Por ejemplo, los modos vibracionales en un cristal, conocidos como fonones, están asociados con fluctuaciones lentas de densidad de los átomos del cristal. El modo Goldstone asociado para los imanes son ondas oscilantes de espín conocidas como ondas de espín. Para los estados de ruptura de simetría, cuyo parámetro de orden no es una cantidad conservada, los modos Nambu-Goldstone normalmente no tienen masa y se propagan a una velocidad constante.
Un teorema importante, debido a Mermin y Wagner, establece que, a temperatura finita, las fluctuaciones activadas térmicamente de los modos Nambu-Goldstone destruyen el orden de largo alcance y evitan la ruptura espontánea de la simetría en sistemas unidimensionales y bidimensionales. De manera similar, las fluctuaciones cuánticas del parámetro de orden evitan la mayoría de los tipos de ruptura continua de la simetría en sistemas unidimensionales incluso a temperatura cero. (Una excepción importante son los ferroimanes, cuyo parámetro de orden, la magnetización, es una cantidad exactamente conservada y no tiene fluctuaciones cuánticas).
Se ha demostrado que otros sistemas de interacción de largo alcance, como las superficies curvas cilíndricas que interactúan a través del potencial de Coulomb o el potencial de Yukawa , rompen las simetrías traslacionales y rotacionales. [13] Se demostró que, en presencia de un hamiltoniano simétrico y en el límite del volumen infinito, el sistema adopta espontáneamente una configuración quiral, es decir, rompe la simetría del plano especular .
Para que se produzca una ruptura espontánea de la simetría, debe existir un sistema en el que existan varios resultados igualmente probables. Por lo tanto, el sistema en su conjunto es simétrico con respecto a estos resultados. Sin embargo, si se toma una muestra del sistema (es decir, si se utiliza o interactúa con él de algún modo), debe producirse un resultado específico. Aunque el sistema en su conjunto es simétrico, nunca se encuentra con esta simetría, sino solo en un estado asimétrico específico. Por lo tanto, se dice que la simetría se rompe espontáneamente en esa teoría. Sin embargo, el hecho de que cada resultado sea igualmente probable es un reflejo de la simetría subyacente, que a menudo se denomina "simetría oculta", y tiene consecuencias formales cruciales. (Véase el artículo sobre el bosón de Goldstone .)
Cuando una teoría es simétrica con respecto a un grupo de simetría , pero requiere que un elemento del grupo sea distinto, entonces se ha producido una ruptura espontánea de la simetría. La teoría no debe dictar qué miembro es distinto, solo que uno lo es . A partir de este punto, la teoría puede tratarse como si este elemento fuera realmente distinto, con la condición de que cualquier resultado que se encuentre de esta manera debe ser resimetrizado, tomando el promedio de cada uno de los elementos del grupo como distinto.
El concepto crucial en las teorías de la física es el parámetro de orden . Si hay un campo (a menudo un campo de fondo) que adquiere un valor esperado (no necesariamente un valor esperado de vacío ) que no es invariante bajo la simetría en cuestión, decimos que el sistema está en la fase ordenada y la simetría se rompe espontáneamente. Esto se debe a que otros subsistemas interactúan con el parámetro de orden, que especifica un "marco de referencia" contra el cual medirse. En ese caso, el estado de vacío no obedece a la simetría inicial (que lo mantendría invariante, en el modo de Wigner realizado linealmente en el que sería un singlete), y, en cambio, cambia bajo la simetría (oculta), ahora implementada en el modo de Nambu-Goldstone (no lineal) . Normalmente, en ausencia del mecanismo de Higgs, surgen bosones de Goldstone sin masa.
El grupo de simetría puede ser discreto, como el grupo espacial de un cristal, o continuo (por ejemplo, un grupo de Lie ), como la simetría rotacional del espacio. Sin embargo, si el sistema contiene solo una única dimensión espacial, entonces solo las simetrías discretas pueden romperse en un estado de vacío de la teoría cuántica completa , aunque una solución clásica puede romper una simetría continua.
El 7 de octubre de 2008, la Real Academia Sueca de Ciencias otorgó el Premio Nobel de Física 2008 a tres científicos por su trabajo en la ruptura de simetría en física subatómica. Yoichiro Nambu , de la Universidad de Chicago , ganó la mitad del premio por el descubrimiento del mecanismo de ruptura espontánea de simetría en el contexto de las interacciones fuertes, específicamente la ruptura de simetría quiral . Los físicos Makoto Kobayashi y Toshihide Maskawa , de la Universidad de Kioto , compartieron la otra mitad del premio por descubrir el origen de la ruptura explícita de la simetría CP en las interacciones débiles. [14] Este origen depende en última instancia del mecanismo de Higgs, pero, hasta ahora entendido como una característica "justo así" de los acoplamientos de Higgs, no un fenómeno de simetría rota espontáneamente.