
La polarización (también llamada polarización de onda ) es una propiedad delas ondas transversalesque especifica la orientación geométrica de lasoscilaciones.[1][2][3][4][5] En una onda transversal, la dirección de la oscilación es perpendicular a la dirección de movimiento de la onda.[4] Un ejemplo simple de una onda transversal polarizada son las vibraciones que viajan a lo largo de una cuerda tensa(ver imagen), por ejemplo, en un instrumento musical como unacuerda de guitarra. Dependiendo de cómo se toque la cuerda, las vibraciones pueden ser en dirección vertical, horizontal o en cualquier ángulo perpendicular a la cuerda. Por el contrario, enlas ondas longitudinales, comolas ondas sonorasen un líquido o gas, el desplazamiento de las partículas en la oscilación siempre está en la dirección de propagación, por lo que estas ondas no presentan polarización. Las ondas transversales que presentan polarización incluyenondas electromagnéticascomode luzyradio,ondas gravitacionales,[6]y ondas sonoras transversales (ondas de corte) en sólidos.
Una onda electromagnética, como la luz, consta de un campo eléctrico oscilante acoplado y un campo magnético que siempre son perpendiculares entre sí; por convención, la "polarización" de las ondas electromagnéticas se refiere a la dirección del campo eléctrico. En la polarización lineal , los campos oscilan en una sola dirección. En la polarización circular o elíptica , los campos giran a una velocidad constante en un plano a medida que la onda viaja, ya sea en la dirección de la derecha o de la izquierda.
La luz u otra radiación electromagnética de muchas fuentes, como el sol, las llamas y las lámparas incandescentes , consiste en trenes de ondas cortas con una mezcla igual de polarizaciones; esto se llama luz no polarizada . La luz polarizada se puede producir al pasar luz no polarizada a través de un polarizador , que permite que pasen ondas de una sola polarización. Los materiales ópticos más comunes no afectan la polarización de la luz, pero algunos materiales (los que presentan birrefringencia , dicroísmo o actividad óptica ) afectan a la luz de manera diferente según su polarización. Algunos de estos se utilizan para hacer filtros polarizadores. La luz también se polariza parcialmente cuando se refleja en un ángulo desde una superficie.
Según la mecánica cuántica , las ondas electromagnéticas también pueden verse como corrientes de partículas llamadas fotones . Cuando se ven de esta manera, la polarización de una onda electromagnética está determinada por una propiedad mecánica cuántica de los fotones llamada su espín . [7] [8] Un fotón tiene uno de dos espines posibles: puede girar en sentido de la mano derecha o en sentido de la mano izquierda sobre su dirección de viaje. Las ondas electromagnéticas polarizadas circularmente están compuestas de fotones con un solo tipo de espín, ya sea derecho o izquierdo. Las ondas polarizadas linealmente consisten en fotones que están en una superposición de estados polarizados circularmente derecho e izquierdo, con amplitud y fases iguales sincronizadas para dar oscilación en un plano. [8]
La polarización es un parámetro importante en áreas científicas que tratan con ondas transversales, como la óptica , la sismología , la radio y las microondas . Se ven especialmente afectadas por tecnologías como los láseres , las telecomunicaciones inalámbricas y por fibra óptica y el radar .
La mayoría de las fuentes de luz se clasifican como incoherentes y no polarizadas (o solo "parcialmente polarizadas") porque consisten en una mezcla aleatoria de ondas que tienen diferentes características espaciales, frecuencias (longitudes de onda), fases y estados de polarización. Sin embargo, para comprender las ondas electromagnéticas y la polarización en particular, es más fácil considerar simplemente las ondas planas coherentes ; estas son ondas sinusoidales de una dirección particular (o vector de onda ), frecuencia, fase y estado de polarización. La caracterización de un sistema óptico en relación con una onda plana con esos parámetros dados se puede utilizar para predecir su respuesta a un caso más general, ya que una onda con cualquier estructura espacial especificada se puede descomponer en una combinación de ondas planas (su llamado espectro angular ). Los estados incoherentes se pueden modelar estocásticamente como una combinación ponderada de tales ondas no correlacionadas con alguna distribución de frecuencias (su espectro ), fases y polarizaciones.
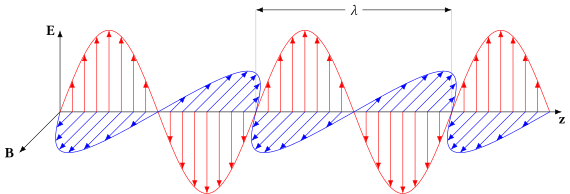
Las ondas electromagnéticas (como la luz), que se propagan en el espacio libre o en otro medio isótropo homogéneo no atenuante , se describen correctamente como ondas transversales , lo que significa que el vector de campo eléctrico E y el campo magnético H de una onda plana están cada uno en alguna dirección perpendicular a (o "transversal" a) la dirección de propagación de la onda; E y H también son perpendiculares entre sí. Por convención, la dirección de "polarización" de una onda electromagnética está dada por su vector de campo eléctrico. Considerando una onda plana monocromática de frecuencia óptica f (la luz de longitud de onda de vacío λ tiene una frecuencia de f = c/λ donde c es la velocidad de la luz), tomemos la dirección de propagación como el eje z . Al ser una onda transversal, los campos E y H deben contener componentes solo en las direcciones x e y , mientras que E z = H z = 0. Usando la notación compleja (o fasorial ), los campos eléctricos y magnéticos físicos instantáneos están dados por las partes reales de las cantidades complejas que ocurren en las siguientes ecuaciones. Como función del tiempo t y la posición espacial z (ya que para una onda plana en la dirección + z los campos no tienen dependencia de x o y ) estos campos complejos pueden escribirse como: y donde λ = λ 0 / n es la longitud de onda en el medio (cuyo índice de refracción es n ) y T = 1/ f es el período de la onda. Aquí e x , e y , h x y h y son números complejos. En la segunda forma más compacta, como se expresan habitualmente estas ecuaciones, estos factores se describen utilizando el número de onda k = 2π n / λ 0 y la frecuencia angular (o "frecuencia en radianes") ω = 2π f . En una formulación más general con propagación no restringida a la +z dirección, entonces la dependencia espacial kz se reemplaza por k → ∙ r → donde k → se llama vector de onda , cuya magnitud es el número de onda.
Por lo tanto, los vectores principales e y h contienen cada uno hasta dos componentes distintos de cero (complejos) que describen la amplitud y la fase de los componentes de polarización x e y de la onda (de nuevo, no puede haber ningún componente de polarización z para una onda transversal en la dirección + z ). Para un medio dado con una impedancia característica η , h está relacionada con e por:
En un dieléctrico, η es real y tiene el valor η 0 / n , donde n es el índice de refracción y η 0 es la impedancia del espacio libre . La impedancia será compleja en un medio conductor. Nótese que, dada esa relación, el producto escalar de E y H debe ser cero: lo que indica que estos vectores son ortogonales (forman ángulos rectos entre sí), como se esperaba.
Conociendo la dirección de propagación ( + z en este caso) y η , se puede especificar la onda en términos de sólo e x y e y que describen el campo eléctrico. El vector que contiene e x y e y (pero sin el componente z que es necesariamente cero para una onda transversal) se conoce como un vector de Jones . Además de especificar el estado de polarización de la onda, un vector de Jones general también especifica la magnitud y fase generales de esa onda. Específicamente, la intensidad de la onda de luz es proporcional a la suma de las magnitudes al cuadrado de los dos componentes del campo eléctrico:
Sin embargo, el estado de polarización de la onda depende únicamente de la relación (compleja) entre e y y e x . Por lo tanto, consideremos ondas cuyo | e x | 2 + | e y | 2 = 1 ; esto corresponde a una intensidad de aproximadamente0,001 33 W /m 2 en el espacio libre (donde η = η 0 ). Y como la fase absoluta de una onda no es importante al analizar su estado de polarización, estipulemos que la fase de e x es cero; en otras palabras, e x es un número real mientras que e y puede ser complejo. Con estas restricciones, e x y e y pueden representarse de la siguiente manera: donde el estado de polarización ahora está completamente parametrizado por el valor de Q (tal que −1 < Q < 1 ) y la fase relativa ϕ .
Además de las ondas transversales, existen muchos movimientos ondulatorios en los que la oscilación no se limita a direcciones perpendiculares a la dirección de propagación. Estos casos quedan fuera del alcance del presente artículo, que se centra en las ondas transversales (como la mayoría de las ondas electromagnéticas en medios masivos), pero conviene tener en cuenta los casos en los que la polarización de una onda coherente no se puede describir simplemente utilizando un vector de Jones, como acabamos de hacer.
Considerando solamente las ondas electromagnéticas, notamos que la discusión precedente se aplica estrictamente a ondas planas en un medio isótropo homogéneo no atenuante, mientras que en un medio anisotrópico (tal como cristales birrefringentes como se discute más adelante) el campo eléctrico o magnético puede tener componentes longitudinales así como transversales. En esos casos el desplazamiento eléctrico D y la densidad de flujo magnético B [ aclaración necesaria ] todavía obedecen a la geometría anterior pero debido a la anisotropía en la susceptibilidad eléctrica (o en la permeabilidad magnética ), ahora dada por un tensor , la dirección de E (o H ) puede diferir de la de D (o B ). Incluso en medios isótropos, las llamadas ondas no homogéneas pueden ser lanzadas a un medio cuyo índice de refracción tiene una parte imaginaria significativa (o " coeficiente de extinción ") tal como metales; [ aclaración necesaria ] estos campos tampoco son estrictamente transversales. [9] : 179–184 [10] : 51–52 Las ondas superficiales o las ondas que se propagan en una guía de ondas (como una fibra óptica ) generalmente no son ondas transversales, sino que podrían describirse como un modo transversal eléctrico o magnético , o un modo híbrido.
Incluso en el espacio libre, se pueden generar componentes de campo longitudinales en regiones focales, donde la aproximación de onda plana se rompe. Un ejemplo extremo es la luz polarizada radial o tangencialmente, en cuyo foco el campo eléctrico o magnético respectivamente es completamente longitudinal (a lo largo de la dirección de propagación). [11]
En el caso de las ondas longitudinales, como las ondas sonoras en fluidos , la dirección de oscilación es, por definición, la dirección de propagación, por lo que normalmente ni siquiera se menciona la cuestión de la polarización. Por otro lado, las ondas sonoras en un sólido a granel pueden ser tanto transversales como longitudinales, lo que da un total de tres componentes de polarización. En este caso, la polarización transversal está asociada a la dirección de la tensión de corte y al desplazamiento en direcciones perpendiculares a la dirección de propagación, mientras que la polarización longitudinal describe la compresión del sólido y la vibración a lo largo de la dirección de propagación. La propagación diferencial de las polarizaciones transversal y longitudinal es importante en sismología .

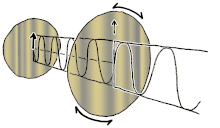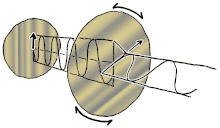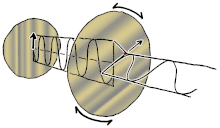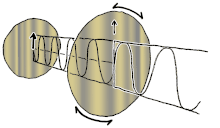
La polarización se puede definir en términos de estados de polarización pura con solo una onda sinusoidal coherente en una frecuencia óptica. El vector en el diagrama adyacente podría describir la oscilación del campo eléctrico emitido por un láser monomodo (cuya frecuencia de oscilación sería típicamente10 15 veces más rápido). El campo oscila en el plano xy , a lo largo de la página, con la onda propagándose en la dirección z , perpendicular a la página. Los primeros dos diagramas a continuación trazan el vector de campo eléctrico durante un ciclo completo para polarización lineal en dos orientaciones diferentes; cada una de ellas se considera un estado de polarización (SOP) distinto. La polarización lineal a 45° también se puede ver como la suma de una onda polarizada linealmente horizontalmente (como en la figura más a la izquierda) y una onda polarizada verticalmente de la misma amplitud en la misma fase .
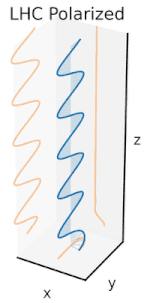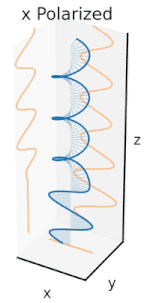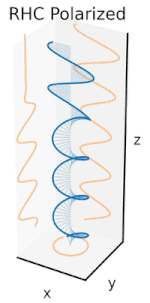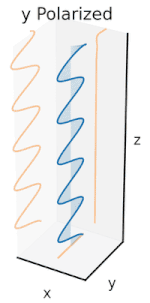
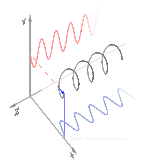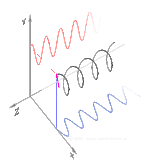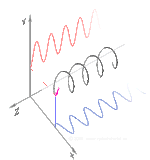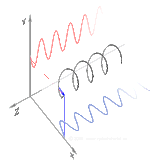
Ahora bien, si se introdujera un cambio de fase entre esos componentes de polarización horizontal y vertical, se obtendría generalmente una polarización elíptica [12], como se muestra en la tercera figura. Cuando el cambio de fase es exactamente de ±90° y las amplitudes son las mismas, se produce una polarización circular (figuras cuarta y quinta). La polarización circular se puede crear enviando luz polarizada linealmente a través de una placa de cuarto de onda orientada a 45° con respecto a la polarización lineal para crear dos componentes de la misma amplitud con el cambio de fase requerido. La superposición de los componentes originales y desfasados provoca un vector de campo eléctrico giratorio, que se muestra en la animación de la derecha. Nótese que la polarización circular o elíptica puede implicar una rotación del campo en el sentido de las agujas del reloj o en el sentido contrario, dependiendo de las fases relativas de los componentes. Estas corresponden a estados de polarización distintos, como las dos polarizaciones circulares que se muestran arriba.
La orientación de los ejes x e y utilizados en esta descripción es arbitraria. La elección de dicho sistema de coordenadas y la visualización de la elipse de polarización en términos de los componentes de polarización x e y corresponden a la definición del vector de Jones (abajo) en términos de esas polarizaciones de base . Los ejes se seleccionan para adaptarse a un problema particular, como por ejemplo, que x esté en el plano de incidencia. Dado que existen coeficientes de reflexión separados para las polarizaciones lineales en y ortogonales al plano de incidencia ( polarizaciones p y s , véase abajo), esa elección simplifica enormemente el cálculo de la reflexión de una onda desde una superficie.
Cualquier par de estados de polarización ortogonales pueden utilizarse como funciones base, no solo polarizaciones lineales. Por ejemplo, la elección de polarizaciones circulares derecha e izquierda como funciones base simplifica la solución de problemas que involucran birrefringencia circular (actividad óptica) o dicroísmo circular.

Para una onda monocromática puramente polarizada, el vector de campo eléctrico a lo largo de un ciclo de oscilación traza una elipse. Entonces, se puede describir un estado de polarización en relación con los parámetros geométricos de la elipse y su "lateralidad", es decir, si la rotación alrededor de la elipse es en el sentido de las agujas del reloj o en el sentido contrario. Una parametrización de la figura elíptica especifica el ángulo de orientación ψ , definido como el ángulo entre el eje mayor de la elipse y el eje x [13] junto con la elipticidad ε = a/b , la relación entre el eje mayor y el eje menor de la elipse. [14] [15] [16] (también conocida como relación axial ). El parámetro de elipticidad es una parametrización alternativa de la excentricidad de una elipse o el ángulo de elipticidad , como se muestra en la figura. [13] El ángulo χ también es significativo porque la latitud (ángulo desde el ecuador) del estado de polarización representado en la esfera de Poincaré (ver más abajo) es igual a ±2 χ . Los casos especiales de polarización lineal y circular corresponden a una elipticidad ε de infinito y unidad (o χ de cero y 45°) respectivamente.
La amplitud y la fase de las oscilaciones en dos componentes del vector de campo eléctrico en el plano de polarización también proporcionan información completa sobre un estado completamente polarizado. Esta representación se utilizó anteriormente para mostrar cómo son posibles diferentes estados de polarización. La información de amplitud y fase se puede representar convenientemente como un vector complejo bidimensional (el vector de Jones ):
Aquí, un 1 y un 2 denotan la amplitud de la onda en los dos componentes del vector de campo eléctrico, mientras que θ 1 y θ 2 representan las fases. El producto de un vector de Jones con un número complejo de módulo unitario da un vector de Jones diferente que representa la misma elipse y, por lo tanto, el mismo estado de polarización. El campo eléctrico físico, como parte real del vector de Jones, se alteraría, pero el estado de polarización en sí es independiente de la fase absoluta . Los vectores base utilizados para representar el vector de Jones no necesitan representar estados de polarización lineal (es decir, ser reales ). En general, se pueden utilizar dos estados ortogonales cualesquiera, donde un par de vectores ortogonales se define formalmente como uno que tiene un producto interno cero . Una opción común son las polarizaciones circulares izquierda y derecha, por ejemplo, para modelar la diferente propagación de ondas en dos de estos componentes en medios circularmente birrefringentes (ver más abajo) o trayectorias de señal de detectores coherentes sensibles a la polarización circular.
Independientemente de si el estado de polarización se representa mediante parámetros geométricos o vectores de Jones, en la parametrización está implícita la orientación del sistema de coordenadas. Esto permite un grado de libertad, a saber, la rotación sobre la dirección de propagación. Cuando se considera la luz que se propaga en paralelo a la superficie de la Tierra, a menudo se utilizan los términos polarización "horizontal" y "vertical", asociándose la primera al primer componente del vector de Jones, o ángulo acimutal cero. Por otro lado, en astronomía se suele utilizar el sistema de coordenadas ecuatorial , correspondiendo el acimut cero (o ángulo de posición, como se le llama más comúnmente en astronomía para evitar confusiones con el sistema de coordenadas horizontales ) al norte exacto.
Otro sistema de coordenadas que se utiliza con frecuencia se relaciona con el plano de incidencia . Este es el plano formado por la dirección de propagación entrante y el vector perpendicular al plano de una interfaz, en otras palabras, el plano en el que viaja el rayo antes y después de la reflexión o refracción. El componente del campo eléctrico paralelo a este plano se denomina p-like (paralelo) y el componente perpendicular a este plano se denomina s-like (de senkrecht , 'perpendicular' en alemán). La luz polarizada con su campo eléctrico a lo largo del plano de incidencia se denota p-polarizada , mientras que la luz cuyo campo eléctrico es normal al plano de incidencia se llama s-polarizada . La p -polarización se conoce comúnmente como transversal-magnética (TM), y también se ha denominado pi-polarizada o π -polarizada , o polarizada en el plano tangencial . La s -polarización también se llama transversal-eléctrica (TE), así como sigma-polarizada o σ-polarizada , o polarizada en el plano sagital .
El grado de polarización ( DOP ) es una cantidad que se utiliza para describir la parte de una onda electromagnética que está polarizada. El DOP se puede calcular a partir de los parámetros de Stokes . Una onda perfectamente polarizada tiene un DOP del 100%, mientras que una onda no polarizada tiene un DOP del 0%. Una onda que está parcialmente polarizada y, por lo tanto, se puede representar mediante una superposición de un componente polarizado y uno no polarizado, tendrá un DOP entre 0 y 100%. El DOP se calcula como la fracción de la potencia total que transporta el componente polarizado de la onda.
La DOP se puede utilizar para mapear el campo de deformación en materiales al considerar la DOP de la fotoluminiscencia . La polarización de la fotoluminiscencia está relacionada con la deformación en un material a través del tensor de fotoelasticidad del material dado .
La DOP también se visualiza utilizando la representación de la esfera de Poincaré de un haz polarizado. En esta representación, la DOP es igual a la longitud del vector medida desde el centro de la esfera.
La luz no polarizada es luz con una polarización aleatoria que varía con el tiempo . La luz natural, como la mayoría de las demás fuentes comunes de luz visible, es producida independientemente por una gran cantidad de átomos o moléculas cuyas emisiones no están correlacionadas .
La luz no polarizada se puede producir a partir de la combinación incoherente de luz polarizada linealmente vertical y horizontal, o luz polarizada circularmente dextrógira y levógira . [17] Por el contrario, los dos estados polarizados linealmente constituyentes de la luz no polarizada no pueden formar un patrón de interferencia , incluso si se rotan para alinearse ( tercera ley de Fresnel-Arago ). [18]
Un despolarizador actúa sobre un haz polarizado para crear uno en el que la polarización varía tan rápidamente a lo largo del haz que puede ignorarse en las aplicaciones previstas. Por el contrario, un polarizador actúa sobre un haz no polarizado o un haz polarizado arbitrariamente para crear uno polarizado.
La luz no polarizada puede describirse como una mezcla de dos corrientes independientes polarizadas de forma opuesta, cada una con la mitad de intensidad. [19] [20] Se dice que la luz está parcialmente polarizada cuando hay más potencia en una de estas corrientes que en la otra. En cualquier longitud de onda particular, la luz parcialmente polarizada puede describirse estadísticamente como la superposición de un componente completamente no polarizado y uno completamente polarizado. [21] : 346–347 [22] : 330 Se puede describir entonces la luz en términos del grado de polarización y los parámetros del componente polarizado. Ese componente polarizado puede describirse en términos de un vector de Jones o una elipse de polarización. Sin embargo, para describir también el grado de polarización, normalmente se emplean los parámetros de Stokes para especificar un estado de polarización parcial. [21] : 351, 374–375En el vacío , las componentes del campo eléctrico se propagan a la velocidad de la luz , de modo que la fase de la onda varía en el espacio y en el tiempo mientras que el estado de polarización no lo hace. Es decir, el vector de campo eléctrico e de una onda plana en la dirección + z es:
donde k es el número de onda . Como se señaló anteriormente, el campo eléctrico instantáneo es la parte real del producto del vector de Jones por el factor de fase . Cuando una onda electromagnética interactúa con la materia, su propagación se altera de acuerdo con el índice de refracción (complejo) del material . Cuando la parte real o imaginaria de ese índice de refracción depende del estado de polarización de una onda, propiedades conocidas como birrefringencia y dicroísmo de polarización (o diatenuación ) respectivamente, entonces el estado de polarización de una onda generalmente se alterará.
En tales medios, una onda electromagnética con cualquier estado de polarización dado puede descomponerse en dos componentes polarizados ortogonalmente que encuentran constantes de propagación diferentes . El efecto de la propagación a lo largo de una trayectoria dada sobre esos dos componentes se caracteriza más fácilmente en forma de una ecuación compleja. Matriz de transformación 2 × 2 J conocida como matriz de Jones :
La matriz de Jones debida al paso a través de un material transparente depende de la distancia de propagación así como de la birrefringencia. La birrefringencia (así como el índice de refracción promedio) generalmente será dispersiva , es decir, variará en función de la frecuencia óptica (longitud de onda). Sin embargo, en el caso de materiales no birrefringentes, laLa matriz de Jones 2 × 2 es la matriz identidad (multiplicada por un factor de fase escalar y un factor de atenuación), lo que implica que no hay cambios en la polarización durante la propagación.
Para los efectos de propagación en dos modos ortogonales, la matriz de Jones se puede escribir como
donde g 1 y g 2 son números complejos que describen el retardo de fase y posiblemente la atenuación de amplitud debido a la propagación en cada uno de los dos modos propios de polarización . T es una matriz unitaria que representa un cambio de base de estos modos de propagación al sistema lineal utilizado para los vectores de Jones; en el caso de birrefringencia o diatenuación lineal, los modos son en sí mismos estados de polarización lineal, por lo que T y T −1 se pueden omitir si los ejes de coordenadas se han elegido adecuadamente.
En una sustancia birrefringente , las ondas electromagnéticas de diferentes polarizaciones viajan a diferentes velocidades ( velocidades de fase ). Como resultado, cuando las ondas no polarizadas viajan a través de una placa de material birrefringente, un componente de polarización tiene una longitud de onda más corta que el otro, lo que resulta en una diferencia de fase entre los componentes que aumenta cuanto más viajan las ondas a través del material. La matriz de Jones es una matriz unitaria : | g 1 | = | g 2 | = 1 . Los medios denominados diatenuantes (o dicroicos en el sentido de polarización), en los que solo las amplitudes de las dos polarizaciones se ven afectadas de manera diferencial, pueden describirse utilizando una matriz hermítica (generalmente multiplicada por un factor de fase común). De hecho, dado que cualquier matriz puede escribirse como el producto de matrices hermíticas unitarias y positivas, la propagación de la luz a través de cualquier secuencia de componentes ópticos dependientes de la polarización puede escribirse como el producto de estos dos tipos básicos de transformaciones.

En los medios birrefringentes no hay atenuación, pero los dos modos acumulan un retardo de fase diferencial. Las manifestaciones bien conocidas de la birrefringencia lineal (es decir, en las que las polarizaciones de base son polarizaciones lineales ortogonales) aparecen en las placas de ondas ópticas /retardadores y en muchos cristales. Si la luz polarizada linealmente pasa a través de un material birrefringente, su estado de polarización generalmente cambiará, a menos que su dirección de polarización sea idéntica a una de esas polarizaciones de base. Dado que el cambio de fase, y por lo tanto el cambio en el estado de polarización, generalmente depende de la longitud de onda, dichos objetos vistos bajo luz blanca entre dos polarizadores pueden dar lugar a efectos coloridos, como se ve en la fotografía adjunta.
La birrefringencia circular también se denomina actividad óptica , especialmente en fluidos quirales , o rotación de Faraday , cuando se debe a la presencia de un campo magnético a lo largo de la dirección de propagación. Cuando la luz polarizada linealmente pasa a través de un objeto de este tipo, saldrá todavía polarizada linealmente, pero con el eje de polarización rotado. Una combinación de birrefringencia lineal y circular tendrá como polarizaciones de base dos polarizaciones elípticas ortogonales; sin embargo, el término "birrefringencia elíptica" rara vez se utiliza.
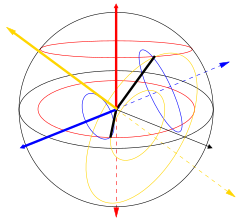
Se puede visualizar el caso de birrefringencia lineal (con dos modos de propagación lineal ortogonales) con una onda entrante polarizada linealmente en un ángulo de 45° con respecto a esos modos. A medida que comienza a acumularse una fase diferencial, la polarización se vuelve elíptica, cambiando eventualmente a polarización puramente circular (diferencia de fase de 90°), luego a polarización elíptica y finalmente a polarización lineal (fase de 180°) perpendicular a la polarización original, luego a circular nuevamente (fase de 270°), luego a elíptica con el ángulo de acimut original y finalmente de regreso al estado de polarización lineal original (fase de 360°) donde el ciclo comienza de nuevo. En general, la situación es más complicada y se puede caracterizar como una rotación en la esfera de Poincaré sobre el eje definido por los modos de propagación. En la figura de la izquierda se muestran ejemplos de birrefringencia lineal (azul), circular (roja) y elíptica (amarilla) . La intensidad total y el grado de polarización no se ven afectados. Si la longitud del camino en el medio birrefringente es suficiente, los dos componentes de polarización de un haz colimado (o rayo ) pueden salir del material con un desfase posicional, aunque sus direcciones de propagación finales sean las mismas (suponiendo que la cara de entrada y la cara de salida sean paralelas). Esto se observa comúnmente utilizando cristales de calcita , que presentan al observador dos imágenes ligeramente desfasadas, en polarizaciones opuestas, de un objeto detrás del cristal. Fue este efecto el que proporcionó el primer descubrimiento de la polarización, por Erasmus Bartholinus en 1669.
Los medios en los que se reduce preferentemente la transmisión de un modo de polarización se denominan dicroicos o diatenuantes . Al igual que la birrefringencia, la diatenuación puede darse con respecto a los modos de polarización lineal (en un cristal) o a los modos de polarización circular (normalmente en un líquido).
Los dispositivos que bloquean casi toda la radiación en un modo se conocen como filtros polarizadores o simplemente " polarizadores ". Esto corresponde a g 2 = 0 en la representación anterior de la matriz de Jones. La salida de un polarizador ideal es un estado de polarización específico (normalmente polarización lineal) con una amplitud igual a la amplitud original de la onda de entrada en ese modo de polarización. La potencia en el otro modo de polarización se elimina. Por tanto, si la luz no polarizada pasa a través de un polarizador ideal (donde g 1 = 1 y g 2 = 0 ) se conserva exactamente la mitad de su potencia inicial. Los polarizadores prácticos, especialmente los polarizadores de láminas económicos, tienen una pérdida adicional de modo que g 1 < 1 . Sin embargo, en muchos casos la cifra de mérito más relevante es el grado de polarización del polarizador o la relación de extinción , que implican una comparación de g 1 con g 2 . Dado que los vectores de Jones se refieren a las amplitudes de las ondas (en lugar de a la intensidad ), cuando se iluminan con luz no polarizada, la potencia restante en la polarización no deseada será ( g 2 / g 1 ) 2 de la potencia en la polarización deseada.
Además de la birrefringencia y el dicroísmo en medios extendidos, los efectos de polarización descriptibles mediante matrices de Jones también pueden ocurrir en la interfaz (reflectiva) entre dos materiales de diferente índice de refracción . Estos efectos se tratan mediante las ecuaciones de Fresnel . Parte de la onda se transmite y parte se refleja; para un material dado, esas proporciones (y también la fase de reflexión) dependen del ángulo de incidencia y son diferentes para las polarizaciones s y p . Por lo tanto, el estado de polarización de la luz reflejada (incluso si inicialmente no está polarizada) generalmente cambia.

Toda luz que incida sobre una superficie con un ángulo de incidencia especial conocido como ángulo de Brewster , donde el coeficiente de reflexión de la polarización p es cero, se reflejará y solo quedará la polarización s . Este principio se emplea en el denominado "polarizador de pila de placas" (véase la figura), en el que parte de la polarización s se elimina por reflexión en cada superficie del ángulo de Brewster, dejando solo la polarización p después de la transmisión a través de muchas de esas superficies. El coeficiente de reflexión generalmente menor de la polarización p también es la base de las gafas de sol polarizadas ; al bloquear la polarización s (horizontal), se elimina la mayor parte del deslumbramiento debido al reflejo de una calle mojada, por ejemplo. [23] : 348–350
En el caso especial e importante de la reflexión con incidencia normal (que no involucra materiales anisotrópicos) no hay polarización s o p particular . Tanto los componentes de polarización x como y se reflejan de manera idéntica y, por lo tanto, la polarización de la onda reflejada es idéntica a la de la onda incidente. Sin embargo, en el caso de polarización circular (o elíptica), la lateralidad del estado de polarización se invierte, ya que por convención esto se especifica en relación con la dirección de propagación. La rotación circular del campo eléctrico alrededor de los ejes xy llamada "diestra" para una onda en la dirección + z es "levógira" para una onda en la dirección − z . Pero en el caso general de reflexión con un ángulo de incidencia distinto de cero, no se puede hacer tal generalización. Por ejemplo, la luz polarizada circularmente a la derecha reflejada desde una superficie dieléctrica en un ángulo rasante, seguirá siendo polarizada a la derecha (pero elípticamente). La luz polarizada lineal reflejada desde un metal con una incidencia no normal generalmente se volverá polarizada elípticamente. Estos casos se manejan utilizando vectores de Jones sobre los que actúan los diferentes coeficientes de Fresnel para los componentes de polarización s y p .
Algunas técnicas de medición óptica se basan en la polarización. En muchas otras técnicas ópticas la polarización es crucial o al menos debe tenerse en cuenta y controlarse; los ejemplos son demasiado numerosos para mencionarlos.

En ingeniería , el fenómeno de la birrefringencia inducida por tensión permite observar fácilmente las tensiones en los materiales transparentes. Como se señaló anteriormente y se ve en la fotografía adjunta, la cromaticidad de la birrefringencia generalmente crea patrones de colores cuando se observa entre dos polarizadores. A medida que se aplican fuerzas externas, se observa la tensión interna inducida en el material. Además, la birrefringencia se observa con frecuencia debido a tensiones "congeladas" en el momento de la fabricación. Esto se observa famosamente en la cinta de celofán , cuya birrefringencia se debe al estiramiento del material durante el proceso de fabricación.
La elipsometría es una técnica potente para medir las propiedades ópticas de una superficie uniforme. Implica medir el estado de polarización de la luz tras la reflexión especular de dicha superficie. Esto se hace normalmente en función del ángulo de incidencia o de la longitud de onda (o de ambos). Dado que la elipsometría se basa en la reflexión, no es necesario que la muestra sea transparente a la luz ni que su parte posterior sea accesible.
La elipsometría se puede utilizar para modelar el índice de refracción (complejo) de una superficie de un material a granel. También es muy útil para determinar los parámetros de una o más capas de película delgada depositadas sobre un sustrato. Debido a sus propiedades de reflexión , no solo se puede predecir la magnitud de los componentes de polarización p y s , sino también sus cambios de fase relativos tras la reflexión, en comparación con las mediciones realizadas con un elipsómetro. Un elipsómetro normal no mide el coeficiente de reflexión real (que requiere una cuidadosa calibración fotométrica del haz de iluminación), sino la relación de las reflexiones p y s , así como el cambio de la elipticidad de polarización (de ahí el nombre) inducido tras la reflexión por la superficie que se está estudiando. Además de su uso en ciencia e investigación, los elipsómetros se utilizan in situ para controlar los procesos de producción, por ejemplo. [24] : 585ff [25] : 632

La propiedad de la birrefringencia (lineal) está muy extendida en los minerales cristalinos y, de hecho, fue fundamental en el descubrimiento inicial de la polarización. En mineralogía , esta propiedad se explota con frecuencia utilizando microscopios de polarización con el fin de identificar minerales. Véase mineralogía óptica para más detalles. [26] : 163–164
Las ondas sonoras en materiales sólidos presentan polarización. La propagación diferencial de las tres polarizaciones a través de la tierra es crucial en el campo de la sismología . Las ondas sísmicas polarizadas horizontal y verticalmente ( ondas transversales ) se denominan SH y SV, mientras que las ondas con polarización longitudinal ( ondas compresivas ) se denominan ondas P. [27] : 48–50 [28] : 56–57
De manera similar, los microscopios de polarización se pueden utilizar para ayudar en la detección de materia extraña en cortes de tejido biológico si es birrefringente; las autopsias a menudo mencionan (la falta o presencia de) "restos extraños polarizables". [29]
Hemos visto (arriba) que la birrefringencia de un tipo de cristal es útil para identificarlo, y por lo tanto la detección de la birrefringencia lineal es especialmente útil en geología y mineralogía . La luz polarizada linealmente generalmente tiene su estado de polarización alterado al transmitirse a través de dicho cristal, lo que hace que se destaque cuando se ve entre dos polarizadores cruzados, como se ve en la fotografía de arriba. Del mismo modo, en química, la rotación de los ejes de polarización en una solución líquida puede ser una medida útil. En un líquido, la birrefringencia lineal es imposible, pero puede haber birrefringencia circular cuando una molécula quiral está en solución. Cuando los enantiómeros diestros y zurdos de dicha molécula están presentes en cantidades iguales (una llamada mezcla racémica ), entonces sus efectos se cancelan. Sin embargo, cuando sólo hay uno (o una preponderancia de uno), como es más frecuente en el caso de las moléculas orgánicas , se observa una birrefringencia circular neta (o actividad óptica ), que revela la magnitud de ese desequilibrio (o la concentración de la propia molécula, cuando se puede suponer que sólo está presente un enantiómero). Esto se mide utilizando un polarímetro en el que se hace pasar luz polarizada a través de un tubo del líquido, en cuyo extremo hay otro polarizador que se gira para anular la transmisión de luz a través de él. [23] : 360–365 [30]
En muchas áreas de la astronomía , el estudio de la radiación electromagnética polarizada del espacio exterior es de gran importancia. Aunque no suele ser un factor en la radiación térmica de las estrellas , la polarización también está presente en la radiación de fuentes astronómicas coherentes (por ejemplo, máseres de hidroxilo o metanol ), y fuentes incoherentes como los grandes lóbulos de radio en galaxias activas, y la radiación de radio de púlsares (que puede, se especula, a veces ser coherente), y también se impone a la luz de las estrellas por la dispersión del polvo interestelar . Además de proporcionar información sobre las fuentes de radiación y dispersión, la polarización también investiga el campo magnético interestelar a través de la rotación de Faraday . [31] : 119, 124 [32] : 336–337 La polarización del fondo cósmico de microondas se está utilizando para estudiar la física del universo muy temprano. [33] [34] La radiación de sincrotrón está inherentemente polarizada. Se ha sugerido que fuentes astronómicas causaron la quiralidad de las moléculas biológicas en la Tierra, [35] pero la selección de quiralidad en cristales inorgánicos se ha propuesto como una teoría alternativa. [36]


La luz no polarizada, después de ser reflejada por una superficie especular (brillante), generalmente obtiene un cierto grado de polarización. Este fenómeno fue observado a principios del siglo XIX por el matemático Étienne-Louis Malus , de quien toma su nombre la ley de Malus . Las gafas de sol polarizadas aprovechan este efecto para reducir el deslumbramiento causado por los reflejos de las superficies horizontales, en particular la carretera que tenemos por delante vista desde un ángulo rasante.
Los usuarios de gafas de sol polarizadas observarán ocasionalmente efectos de polarización involuntarios, como efectos de birrefringencia dependientes del color, por ejemplo, en vidrio templado (por ejemplo, ventanas de automóviles) o artículos hechos de plásticos transparentes , junto con la polarización natural por reflexión o dispersión. La luz polarizada de los monitores LCD (ver a continuación) es extremadamente visible cuando se usan estos.

La polarización se observa en la luz del cielo , ya que se debe a la luz solar dispersada por los aerosoles a medida que pasa a través de la atmósfera terrestre . La luz dispersa produce el brillo y el color en los cielos despejados. Esta polarización parcial de la luz dispersa se puede utilizar para oscurecer el cielo en fotografías, lo que aumenta el contraste. Este efecto se observa con mayor intensidad en los puntos del cielo que forman un ángulo de 90° con el Sol. Los filtros polarizadores utilizan estos efectos para optimizar los resultados de las fotografías de escenas en las que interviene la reflexión o la dispersión por parte del cielo. [23] : 346–347 [37] : 495–499

La polarización del cielo se ha utilizado para la orientación en la navegación. La brújula celeste Pfund se utilizó en la década de 1950 para navegar cerca de los polos del campo magnético de la Tierra cuando ni el sol ni las estrellas eran visibles (por ejemplo, bajo nubes diurnas o al anochecer ). Se ha sugerido, de forma controvertida, que los vikingos explotaron un dispositivo similar (la " piedra solar ") en sus extensas expediciones a través del Atlántico Norte en los siglos IX-XI, antes de la llegada de la brújula magnética de Asia a Europa en el siglo XII. Relacionado con la brújula celeste está el " reloj polar ", inventado por Charles Wheatstone a finales del siglo XIX. [38] : 67–69
El principio de la tecnología de pantalla de cristal líquido (LCD) se basa en la rotación del eje de polarización lineal por parte de la matriz de cristal líquido. La luz de la luz de fondo (o la capa reflectante posterior, en dispositivos que no incluyen o requieren una luz de fondo) pasa primero a través de una lámina polarizadora lineal. Esa luz polarizada pasa a través de la capa de cristal líquido real que puede estar organizada en píxeles (para un televisor o un monitor de computadora) o en otro formato, como una pantalla de siete segmentos o una con símbolos personalizados para un producto en particular. La capa de cristal líquido se produce con una quiralidad constante dextrógira (o levógira), que consiste esencialmente en pequeñas hélices . Esto causa birrefringencia circular y está diseñada para que haya una rotación de 90 grados del estado de polarización lineal. Sin embargo, cuando se aplica un voltaje a través de una celda, las moléculas se enderezan, disminuyendo o perdiendo totalmente la birrefringencia circular. En el lado de visualización de la pantalla hay otra lámina polarizadora lineal, generalmente orientada a 90 grados de la que está detrás de la capa activa. Por lo tanto, cuando se elimina la birrefringencia circular mediante la aplicación de un voltaje suficiente, la polarización de la luz transmitida permanece en ángulo recto con el polarizador frontal y el píxel aparece oscuro. Sin embargo, sin voltaje, la rotación de 90 grados de la polarización hace que coincida exactamente con el eje del polarizador frontal, lo que permite el paso de la luz. Los voltajes intermedios crean una rotación intermedia del eje de polarización y el píxel tiene una intensidad intermedia. Las pantallas basadas en este principio están muy extendidas y ahora se utilizan en la gran mayoría de televisores, monitores de ordenador y proyectores de vídeo, lo que hace que la tecnología CRT anterior quede esencialmente obsoleta. El uso de la polarización en el funcionamiento de las pantallas LCD es inmediatamente evidente para alguien que lleva gafas de sol polarizadas, lo que a menudo hace que la pantalla sea ilegible.
En un sentido totalmente diferente, la codificación por polarización se ha convertido en el método principal (pero no único) para entregar imágenes separadas al ojo izquierdo y derecho en las pantallas estereoscópicas utilizadas para películas en 3D . Esto implica imágenes separadas destinadas a cada ojo, ya sea proyectadas desde dos proyectores diferentes con filtros polarizadores orientados ortogonalmente o, más típicamente, desde un solo proyector con polarización multiplexada en el tiempo (un dispositivo de polarización alternante rápido para fotogramas sucesivos). Las gafas 3D polarizadas con filtros polarizadores adecuados garantizan que cada ojo reciba solo la imagen deseada. Históricamente, estos sistemas usaban codificación por polarización lineal porque era económica y ofrecía una buena separación. Sin embargo, la polarización circular hace que la separación de las dos imágenes sea insensible a la inclinación de la cabeza, y se usa ampliamente en la exhibición de películas en 3D en la actualidad, como el sistema de RealD . Proyectar tales imágenes requiere pantallas que mantengan la polarización de la luz proyectada cuando se ve reflejada (como las pantallas plateadas ); una pantalla de proyección blanca difusa normal causa la despolarización de las imágenes proyectadas, lo que la hace inadecuada para esta aplicación.
Aunque ya están obsoletas, las pantallas de ordenador CRT sufrían de reflejos en la envoltura de cristal, lo que provocaba deslumbramiento por las luces de la habitación y, en consecuencia, un contraste deficiente. Se emplearon varias soluciones antirreflejos para mejorar este problema. Una solución utilizó el principio de reflexión de la luz polarizada circularmente. Un filtro polarizador circular delante de la pantalla permite la transmisión (por ejemplo) solo de luz de la habitación polarizada circularmente hacia la derecha. Ahora, la luz polarizada circularmente hacia la derecha (según la convención utilizada) tiene su dirección de campo eléctrico (y magnético) girando en el sentido de las agujas del reloj mientras se propaga en la dirección +z. Tras la reflexión, el campo sigue teniendo la misma dirección de rotación, pero ahora la propagación es en la dirección -z, lo que hace que la onda reflejada esté polarizada circularmente hacia la izquierda . Con el filtro de polarización circular hacia la derecha colocado delante del cristal reflectante, la luz no deseada reflejada desde el cristal estará en el mismo estado de polarización que bloquea ese filtro, lo que elimina el problema de la reflexión. La inversión de la polarización circular en la reflexión y la eliminación de los reflejos de esta manera se pueden observar fácilmente mirándose en un espejo mientras se usan anteojos para películas en 3D que emplean polarización circular izquierda y derecha en las dos lentes. Al cerrar un ojo, el otro ojo verá un reflejo en el que no se puede ver a sí mismo; esa lente aparece negra. Sin embargo, la otra lente (del ojo cerrado) tendrá la polarización circular correcta, lo que permitirá que el ojo cerrado pueda ver fácilmente el ojo abierto.
Todas las antenas de radio (y microondas) utilizadas para transmitir o recibir están intrínsecamente polarizadas. Transmiten en (o reciben señales de) una polarización particular, siendo totalmente insensibles a la polarización opuesta; en ciertos casos, esa polarización es una función de la dirección. La mayoría de las antenas están nominalmente polarizadas linealmente, pero la polarización elíptica y circular es una posibilidad. En el caso de la polarización lineal, es posible el mismo tipo de filtrado que el descrito anteriormente. En el caso de la polarización elíptica (la polarización circular es en realidad solo un tipo de polarización elíptica donde la longitud de ambos factores de elasticidad es la misma), filtrar un solo ángulo (por ejemplo, 90°) prácticamente no tendrá impacto, ya que la onda en cualquier momento puede estar en cualquiera de los 360 grados.
La gran mayoría de las antenas están polarizadas linealmente. De hecho, se puede demostrar a partir de consideraciones de simetría que una antena que se encuentra completamente en un plano que también incluye al observador, solo puede tener su polarización en la dirección de ese plano. Esto se aplica a muchos casos, lo que permite inferir fácilmente la polarización de dicha antena en una dirección de propagación deseada. Por lo tanto, una antena Yagi o log-periódica típica en un tejado con conductores horizontales, vista desde una segunda estación hacia el horizonte, está necesariamente polarizada horizontalmente. Pero una " antena de látigo " vertical o una torre de transmisión de AM utilizada como elemento de antena (de nuevo, para observadores desplazados horizontalmente de ella) transmitirá en polarización vertical. Una antena de torniquete con sus cuatro brazos en el plano horizontal, del mismo modo transmite radiación polarizada horizontalmente hacia el horizonte. Sin embargo, cuando esa misma antena de torniquete se utiliza en el "modo axial" (hacia arriba, para la misma estructura orientada horizontalmente), su radiación está polarizada circularmente. En elevaciones intermedias está polarizada elípticamente.
La polarización es importante en las comunicaciones por radio porque, por ejemplo, si se intenta utilizar una antena polarizada horizontalmente para recibir una transmisión polarizada verticalmente, la intensidad de la señal se reducirá sustancialmente (o, en condiciones muy controladas, se reducirá a cero). Este principio se utiliza en la televisión por satélite para duplicar la capacidad del canal en una banda de frecuencia fija. El mismo canal de frecuencia se puede utilizar para dos señales transmitidas en polarizaciones opuestas. Al ajustar la antena receptora para una u otra polarización, se puede seleccionar cualquiera de las dos señales sin interferencias de la otra.
Especialmente debido a la presencia del suelo , existen algunas diferencias en la propagación (y también en las reflexiones responsables de las imágenes fantasma de TV ) entre las polarizaciones horizontal y vertical. La radiodifusión AM y FM suele utilizar polarización vertical, mientras que la televisión utiliza polarización horizontal. En las frecuencias bajas, especialmente, se evita la polarización horizontal. Esto se debe a que la fase de una onda polarizada horizontalmente se invierte al reflejarse en el suelo. Una estación distante en la dirección horizontal recibirá tanto la onda directa como la reflejada, que tienden a cancelarse entre sí. Este problema se evita con la polarización vertical. La polarización también es importante en la transmisión de pulsos de radar y la recepción de reflexiones de radar por la misma antena o una diferente. Por ejemplo, la retrodispersión de pulsos de radar por gotas de lluvia se puede evitar utilizando polarización circular. Así como la reflexión especular de la luz polarizada circularmente invierte la lateralidad de la polarización, como se explicó anteriormente, el mismo principio se aplica a la dispersión por objetos mucho más pequeños que una longitud de onda, como las gotas de lluvia. Por otra parte, la reflexión de esa onda por un objeto metálico irregular (como un avión) normalmente introducirá un cambio en la polarización y la recepción (parcial) de la onda de retorno por la misma antena.
El efecto de los electrones libres en la ionosfera , en conjunción con el campo magnético de la Tierra , causa la rotación de Faraday , una especie de birrefringencia circular. Este es el mismo mecanismo que puede rotar el eje de polarización lineal por electrones en el espacio interestelar como se menciona a continuación. La magnitud de la rotación de Faraday causada por un plasma de este tipo se exagera mucho en frecuencias más bajas, por lo que en las frecuencias de microondas más altas utilizadas por los satélites el efecto es mínimo. Sin embargo, las transmisiones de onda media o corta recibidas después de la refracción por la ionosfera se ven fuertemente afectadas. Dado que la trayectoria de una onda a través de la ionosfera y el vector del campo magnético de la Tierra a lo largo de dicha trayectoria son bastante impredecibles, una onda transmitida con polarización vertical (u horizontal) generalmente tendrá una polarización resultante en una orientación arbitraria en el receptor.

Muchos animales son capaces de percibir algunos de los componentes de la polarización de la luz, por ejemplo, la luz polarizada horizontalmente lineal. Esto se utiliza generalmente para fines de navegación, ya que la polarización lineal de la luz del cielo siempre es perpendicular a la dirección del sol. Esta capacidad es muy común entre los insectos , incluidas las abejas , que utilizan esta información para orientar sus danzas comunicativas . [38] : 102–103 La sensibilidad a la polarización también se ha observado en especies de pulpos , calamares , sepias y camarones mantis . [38] : 111–112 En el último caso, una especie mide los seis componentes ortogonales de la polarización y se cree que tiene una visión de polarización óptima. [39] Los patrones de piel de colores vivos y rápidamente cambiantes de las sepias, utilizados para la comunicación, también incorporan patrones de polarización, y se sabe que los camarones mantis tienen tejido reflectante selectivo de polarización. Se creía que las palomas percibían la polarización del cielo , lo que se suponía que era una de sus ayudas para orientarse , pero las investigaciones indican que se trata de un mito popular. [40]
El ojo humano desnudo es débilmente sensible a la polarización, sin necesidad de filtros intermedios. La luz polarizada crea un patrón muy tenue cerca del centro del campo visual, llamado pincel de Haidinger . Este patrón es muy difícil de ver, pero con la práctica se puede aprender a detectar la luz polarizada a simple vista. [38] : 118
Es bien sabido que la radiación electromagnética tiene un cierto momento lineal en la dirección de propagación. Además, sin embargo, la luz tiene un cierto momento angular si está polarizada circularmente (o parcialmente). En comparación con frecuencias más bajas, como las microondas, la cantidad de momento angular en la luz , incluso de polarización circular pura, en comparación con el momento lineal de la misma onda (o presión de radiación ) es muy pequeña y difícil incluso de medir. Sin embargo, se utilizó en un experimento para lograr velocidades de hasta 600 millones de revoluciones por minuto. [41] [42]
Física cuántica
Óptica
{{cite book}}: CS1 maint: postscript (link)