El modelo de cielo de Rayleigh describe el patrón de polarización observado en el cielo diurno . Dentro de la atmósfera, la dispersión de luz de Rayleigh por las moléculas de aire , agua, polvo y aerosoles hace que la luz del cielo tenga un patrón de polarización definido. Los mismos procesos de dispersión elástica hacen que el cielo sea azul . La polarización se caracteriza en cada longitud de onda por su grado de polarización y orientación (el ángulo del vector e o ángulo de dispersión).
El patrón de polarización del cielo depende de la posición celestial del Sol . Si bien toda la luz dispersa está polarizada hasta cierto punto, la luz está altamente polarizada en un ángulo de dispersión de 90° desde la fuente de luz. En la mayoría de los casos, la fuente de luz es el Sol, pero la Luna también crea el mismo patrón. El grado de polarización primero aumenta con el aumento de la distancia al Sol y luego disminuye a medida que se aleja del Sol. Por lo tanto, el grado máximo de polarización se produce en una banda circular a 90° del Sol. En esta banda, normalmente se alcanzan grados de polarización cercanos al 80%.

Cuando el Sol se encuentra en el cenit , la banda de polarización máxima envuelve el horizonte . La luz del cielo está polarizada horizontalmente a lo largo del horizonte. Durante el crepúsculo , ya sea en el equinoccio de primavera o de otoño , la banda de polarización máxima está definida por el plano norte-cenit-sur, o meridiano . En particular, la polarización es vertical en el horizonte en el norte y el sur, donde el meridiano se encuentra con el horizonte. La polarización en el crepúsculo de un equinoccio está representada por la figura de la derecha. La banda roja representa el círculo en el plano norte-cenit-sur donde el cielo está altamente polarizado. Las direcciones cardinales (N, E, S, O) se muestran a las 12 en punto, las 9 en punto, las 6 en punto y las 3 en punto (en sentido antihorario alrededor de la esfera celeste , ya que el observador está mirando hacia el cielo).
Tenga en cuenta que, dado que el patrón de polarización depende del Sol, no solo cambia a lo largo del día sino también a lo largo del año. Cuando el Sol se pone hacia el Sur, en el invierno del hemisferio norte, el plano Norte-Cenit-Sur está desfasado, y el Norte "efectivo" en realidad se encuentra algo más hacia el Oeste. Por lo tanto, si el Sol se pone en un acimut de 255° (15° al Sur del Oeste), el patrón de polarización alcanzará su máximo a lo largo del horizonte en un acimut de 345° (15° al Oeste del Norte) y 165° (15° al Este del Sur).
Durante un mismo día, el patrón rota con la posición cambiante del sol. Al anochecer, normalmente aparece unos 45 minutos antes del amanecer local y desaparece 45 minutos después del atardecer local. Una vez establecido, es muy estable y solo muestra cambios en su rotación. Se puede ver fácilmente cualquier día con gafas de sol polarizadas.
Muchos animales utilizan los patrones de polarización del cielo al anochecer y durante el día como herramienta de navegación . Dado que están determinados únicamente por la posición del Sol, se utilizan fácilmente como brújula para la orientación animal. Al orientarse con respecto a los patrones de polarización, los animales pueden localizar el Sol y, de este modo, determinar los puntos cardinales.

La geometría de la polarización del cielo se puede representar mediante un triángulo celeste basado en el Sol, el cenit y la orientación observada (o el punto de dispersión). En el modelo, γ es la distancia angular entre la orientación observada y el Sol, Θ s es la distancia cenital solar (90° – altitud solar), Θ es la distancia angular entre la orientación observada y el cenit (90° – altitud observada), Φ es el ángulo entre la dirección cenital y la dirección solar en la orientación observada, y ψ es el ángulo entre la dirección solar y la orientación observada en el cenit.
De esta forma, el triángulo esférico se define no sólo por los tres puntos situados en el Sol, el cenit y el punto observado, sino por los tres ángulos interiores y las tres distancias angulares. En una cuadrícula altitud - acimut , la distancia angular entre el punto observado y el Sol y la distancia angular entre el punto observado y el cenit cambian, mientras que la distancia angular entre el Sol y el cenit permanece constante en un punto del tiempo.

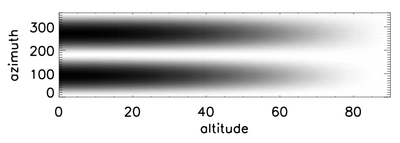
La figura de la izquierda muestra las dos distancias angulares cambiantes tal como se representan en una cuadrícula de altitud-acimut (con la altitud ubicada en el eje x y el acimut ubicado en el eje y). El gráfico superior representa la distancia angular cambiante entre la orientación observada y el Sol, que es opuesta al ángulo interior ubicado en el cenit (o el ángulo de dispersión). Cuando el Sol está ubicado en el cenit, esta distancia es mayor a lo largo del horizonte en todas las direcciones cardinales. Luego disminuye con el aumento de la altitud a medida que se acerca al cenit. Al anochecer, el Sol se pone en el oeste. Por lo tanto, la distancia es mayor cuando se mira directamente lejos del Sol a lo largo del horizonte en el este, y menor a lo largo del horizonte en el oeste.
El gráfico inferior de la figura de la izquierda representa la distancia angular desde el punto de observación hasta el cenit, que es opuesta al ángulo interior situado en el Sol. A diferencia de la distancia entre el punto de observación y el Sol, esta distancia es independiente del acimut, es decir, la dirección cardinal. Es simplemente máxima a lo largo del horizonte a bajas altitudes y disminuye linealmente con el aumento de la altitud.

La figura de la derecha representa las tres distancias angulares. La de la izquierda representa el ángulo en la orientación observada entre la dirección cenital y la dirección solar. Por lo tanto, esto depende en gran medida del cambio de dirección solar a medida que se percibe el Sol en movimiento a través del cielo. La del medio representa el ángulo en el Sol entre la dirección cenital y la orientación. De nuevo, esto depende en gran medida del cambio de orientación. Esto es simétrico entre los hemisferios norte y sur. La de la derecha representa el ángulo en el cenit entre la dirección solar y la orientación. Por lo tanto, gira alrededor de la esfera celeste.
El modelo de cielo de Rayleigh predice el grado de polarización del cielo como:

Como ejemplo sencillo, se puede representar gráficamente el grado de polarización en el horizonte. Como se ve en la figura de la derecha, es alto en el norte (0° y 360°) y en el sur (180°). Luego se asemeja a una función coseno y disminuye hacia el este y el oeste, llegando a cero en estas direcciones cardinales.
El grado de polarización se entiende fácilmente cuando se representa en una cuadrícula de altitud-acimut como se muestra a continuación. A medida que el sol se pone hacia el oeste, el grado máximo de polarización se puede ver en el plano Norte-Cenit-Sur. A lo largo del horizonte, a una altitud de 0° es más alto en el Norte y el Sur, y más bajo en el Este y el Oeste. Luego, a medida que aumenta la altitud acercándose al cenit (o el plano de máxima polarización), la polarización permanece alta en el Norte y el Sur y aumenta hasta que vuelve a ser máxima a 90° en el Este y el Oeste, donde se encuentra en el cenit y dentro del plano de polarización.

Haga clic en la imagen adyacente para ver una animación que representa el grado de polarización tal como se muestra en la esfera celeste. El negro representa las áreas donde el grado de polarización es cero, mientras que el rojo representa las áreas donde el grado de polarización es mucho mayor. Es aproximadamente el 80%, que es un máximo realista para el cielo despejado de Rayleigh durante el día. El video comienza cuando el sol está ligeramente por encima del horizonte y en un acimut de 120°. El cielo está altamente polarizado en el plano efectivo Norte-Cenit-Sur. Esto está ligeramente desfasado porque el acimut del sol no es el Este. El sol se mueve a través del cielo con claros patrones de polarización circular a su alrededor. Cuando el sol está ubicado en el cenit, la polarización es independiente del acimut y disminuye con la altitud ascendente (a medida que se acerca al sol). El patrón continúa a medida que el sol se acerca al horizonte una vez más para la puesta del sol. El video termina con el sol debajo del horizonte.

El plano de dispersión es el plano que pasa por el Sol, el observador y el punto observado (o punto de dispersión). El ángulo de dispersión, γ, es la distancia angular entre el Sol y el punto observado. La ecuación para el ángulo de dispersión se deriva de la ley de los cosenos del triángulo esférico (consulte la figura anterior en la sección de geometría). Viene dada por:
En la ecuación anterior, ψ s y θ s son respectivamente el ángulo acimutal y cenital del Sol, y ψ y θ son respectivamente el ángulo acimutal y cenital del punto observado.
Esta ecuación se rompe en el cenit, donde la distancia angular entre la orientación observada y el cenit, θ s, es 0. Aquí la orientación de la polarización se define como la diferencia de acimut entre la orientación observada y el acimut solar.
El ángulo de polarización (o ángulo de polarización) se define como el ángulo relativo entre un vector tangente al meridiano del punto observado y un ángulo perpendicular al plano de dispersión.
Los ángulos de polarización muestran un cambio regular en el ángulo de polarización con el acimut. Por ejemplo, cuando el sol se pone en el oeste, los ángulos de polarización se desplazan alrededor del horizonte. En este momento, el grado de polarización es constante en bandas circulares centradas alrededor del sol. Por lo tanto, el grado de polarización, así como su ángulo correspondiente, se desplazan claramente alrededor del horizonte. Cuando el sol se encuentra en el cenit, el horizonte representa un grado de polarización constante. El ángulo de polarización correspondiente sigue desplazándose en diferentes direcciones hacia el cenit desde diferentes puntos.
El vídeo de la derecha representa el ángulo de polarización representado en la esfera celeste. Comienza con el Sol situado de forma similar. El ángulo es cero a lo largo de la línea que va del Sol al cenit y aumenta en el sentido de las agujas del reloj hacia el Este a medida que el punto observado se mueve en el mismo sentido de las agujas del reloj hacia el Este. Una vez que el Sol sale por el Este, el ángulo actúa de forma similar hasta que el Sol empieza a moverse por el cielo. A medida que el Sol se mueve por el cielo, el ángulo es tanto cero como alto a lo largo de la línea definida por el Sol, el cenit y el antisol. Es más bajo al Sur de esta línea y más alto al Norte de esta línea. Cuando el Sol está en el cenit, el ángulo es totalmente positivo o 0. Estos dos valores rotan hacia el Oeste. El vídeo luego repite una forma similar cuando el Sol se pone por el Oeste.

El ángulo de polarización se puede descomponer en los parámetros de Stokes Q y U. Q y U se definen como las intensidades polarizadas linealmente a lo largo de los ángulos de posición 0° y 45° respectivamente; -Q y -U son a lo largo de los ángulos de posición 90° y −45°.
Si el sol se encuentra en el horizonte hacia el oeste, el grado de polarización se encuentra entonces a lo largo del plano Norte-Cenit-Sur. Si el observador mira hacia el oeste y al cenit, la polarización es horizontal con respecto al observador. En esta dirección, Q es 1 y U es 0. Si el observador sigue mirando hacia el oeste pero en su lugar mira hacia el norte, la polarización es vertical con respecto a él. Por lo tanto, Q es -1 y U sigue siendo 0. A lo largo del horizonte, U siempre es 0. Q siempre es -1, excepto en el este y el oeste.
El ángulo de dispersión (el ángulo en el cenit entre la dirección solar y la dirección del observador) a lo largo del horizonte es un círculo. De Este a Oeste es de 180° y de Oeste a Este es de 90° al anochecer. Cuando el sol se pone en el Oeste, el ángulo es entonces de 180° de Este a Oeste, y solo de 90° de Oeste a Este. El ángulo de dispersión a una altitud de 45° es constante.
Los parámetros de entrada de Stokes q y u son entonces con respecto al Norte pero en el marco de referencia altitud-acimut. Podemos desdoblar fácilmente q suponiendo que está en la dirección +altitud. De la definición básica sabemos que +Q es un ángulo de 0° y -Q es un ángulo de 90°. Por lo tanto, Q se calcula a partir de una función seno. De manera similar, U se calcula a partir de una función coseno. El ángulo de polarización siempre es perpendicular al plano de dispersión. Por lo tanto, se suman 90° a ambos ángulos de dispersión para encontrar los ángulos de polarización. A partir de esto, se determinan los parámetros de Stokes Q y U:
y
El ángulo de dispersión, derivado de la ley de los cosenos, es con respecto al Sol. El ángulo de polarización es el ángulo con respecto al cenit, o altitud positiva. Existe una línea de simetría definida por el Sol y el cenit. Se traza desde el Sol a través del cenit hasta el otro lado de la esfera celeste donde estaría el "antisol". Este es también el plano efectivo Este-Cenit-Oeste.


La primera imagen de la derecha representa la entrada q proyectada sobre la esfera celeste. Es simétrica respecto de la línea definida por el sol-cenit-antisol. Al anochecer, en el plano Norte-Cenit-Sur es negativa porque es vertical con el grado de polarización. Es horizontal o positiva en el plano Este-Cenit-Oeste. En otras palabras, es positiva en la dirección ±altitud y negativa en la dirección ±acimut. A medida que el sol se mueve a través del cielo, la entrada q permanece alta a lo largo de la línea sol-cenit-antisol. Permanece cero alrededor de un círculo basado en el sol y el cenit. A medida que pasa el cenit, rota hacia el sur y repite el mismo patrón hasta la puesta del sol.
La segunda imagen a la derecha representa la entrada u asignada a la esfera celeste. El parámetro u de Stokes cambia de signo según el cuadrante en el que se encuentre. Los cuatro cuadrantes están definidos por la línea de simetría, el plano efectivo Este-Cenit-Oeste y el plano Norte-Cenit-Sur. No es simétrico porque está definido por los ángulos ±45°. En cierto sentido, forma dos círculos alrededor de la línea de simetría en lugar de uno solo.
Esto se entiende fácilmente si se compara con la entrada q. Cuando la entrada q está a medio camino entre 0° y 90°, la entrada u es positiva a +45° o negativa a −45°. De manera similar, si la entrada q es positiva a 90° o negativa a 0°, la entrada u está a medio camino entre +45° y −45°. Esto se puede ver en los círculos no simétricos alrededor de la línea de simetría. Luego sigue el mismo patrón a través del cielo que la entrada q.
Las zonas en las que el grado de polarización es cero (la claraboya no está polarizada) se denominan puntos neutros. En estos casos, los parámetros de Stokes Q y U también son iguales a cero por definición. Por tanto, el grado de polarización aumenta con la distancia a los puntos neutros.
Estas condiciones se cumplen en algunos lugares definidos del cielo. El punto Arago se encuentra por encima del punto antisolar, mientras que los puntos Babinet y Brewster se encuentran por encima y por debajo del sol respectivamente. La distancia cenital del punto Babinet o Arago aumenta con la distancia cenital solar. Estos puntos neutrales pueden desviarse de sus posiciones normales debido a la interferencia del polvo y otros aerosoles.
La polarización de la luz del cielo cambia de negativa a positiva al pasar por un punto neutro paralelo al meridiano solar o antisolar. Las líneas que separan las regiones de Q positivo y Q negativo se denominan líneas neutras.
El cielo Rayleigh produce un patrón de polarización claramente definido en muchas circunstancias diferentes. Sin embargo, el grado de polarización no siempre permanece constante y, de hecho, puede disminuir en diferentes situaciones. El cielo Rayleigh puede sufrir despolarización debido a objetos cercanos, como nubes y grandes superficies reflectantes, como el océano. También puede cambiar según la hora del día (por ejemplo, al anochecer o por la noche).
Por la noche, la polarización del cielo iluminado por la luna se reduce considerablemente en presencia de contaminación lumínica urbana , porque la luz urbana dispersa no está fuertemente polarizada. [2]

Numerosas investigaciones demuestran que el ángulo de polarización en un cielo despejado continúa debajo de las nubes si el aire debajo de las nubes recibe la luz solar directa. La dispersión de la luz solar directa sobre esas nubes produce el mismo patrón de polarización. En otras palabras, la proporción del cielo que sigue el modelo de cielo de Rayleigh es alta tanto en cielos despejados como en cielos nublados. El patrón también es claramente visible en pequeñas áreas visibles del cielo. El ángulo de polarización celeste no se ve afectado por las nubes.
Los patrones de polarización se mantienen constantes incluso cuando el Sol no está presente en el cielo. Los patrones crepusculares se producen durante el período de tiempo entre el comienzo del crepúsculo astronómico (cuando el Sol está a 18° por debajo del horizonte) y el amanecer, o el atardecer y el final del crepúsculo astronómico. La duración del crepúsculo astronómico depende de la longitud del camino que recorre el Sol debajo del horizonte. Por lo tanto, depende de la época del año y de la ubicación, pero puede durar hasta 1,5 horas.
El patrón de polarización causado por el crepúsculo se mantiene bastante constante durante este período de tiempo. Esto se debe a que el sol se mueve por debajo del horizonte casi perpendicularmente a él y, por lo tanto, su acimut cambia muy lentamente durante este período de tiempo.
Al anochecer, la luz polarizada dispersa se origina en la atmósfera superior y luego atraviesa toda la atmósfera inferior antes de llegar al observador. Esto brinda múltiples oportunidades de dispersión y causa despolarización. Se ha observado que la polarización aumenta aproximadamente un 10 % desde el inicio del crepúsculo hasta el amanecer. Por lo tanto, el patrón permanece constante mientras que el grado cambia ligeramente.
Los patrones de polarización no sólo se mantienen constantes a medida que el sol se desplaza por el cielo, sino también a medida que la luna se desplaza por el cielo durante la noche. La luna crea el mismo patrón de polarización, por lo que es posible utilizar los patrones de polarización como herramienta para la navegación nocturna. La única diferencia es que el grado de polarización no es tan fuerte.
Las propiedades superficiales subyacentes pueden afectar el grado de polarización del cielo diurno. El grado de polarización depende en gran medida de las propiedades de la superficie. A medida que aumenta la reflectancia de la superficie o el espesor óptico, el grado de polarización disminuye. Por lo tanto, el cielo de Rayleigh cerca del océano puede estar muy despolarizado.
Por último, existe una clara dependencia de la longitud de onda en la dispersión de Rayleigh. Es máxima en longitudes de onda cortas, mientras que la polarización de la luz del cielo es máxima en longitudes de onda medias y largas. Inicialmente es máxima en el ultravioleta, pero a medida que la luz se desplaza hacia la superficie de la Tierra e interactúa a través de la dispersión por múltiples caminos, se vuelve alta en longitudes de onda medias y largas. El ángulo de polarización no muestra variación con la longitud de onda.
Muchos animales, sobre todo los insectos, son sensibles a la polarización de la luz y, por tanto, pueden utilizar los patrones de polarización del cielo diurno como herramienta de orientación. Esta teoría fue propuesta por primera vez por Karl von Frisch al estudiar la orientación celestial de las abejas. El patrón de polarización natural del cielo sirve como una brújula que se detecta fácilmente. A partir de los patrones de polarización, estas especies pueden orientarse determinando la posición exacta del Sol sin necesidad de utilizar la luz solar directa. Así, en cielos nublados, o incluso de noche, los animales pueden encontrar su camino.
Sin embargo, utilizar la luz polarizada como brújula no es una tarea fácil. El animal debe ser capaz de detectar y analizar la luz polarizada. Estas especies tienen fotorreceptores especializados en los ojos que responden a la orientación y el grado de polarización cerca del cenit. Pueden extraer información sobre la intensidad y la orientación del grado de polarización. Luego pueden incorporar esto visualmente para orientarse y reconocer diferentes propiedades de las superficies.
Hay pruebas claras de que los animales pueden orientarse incluso cuando el Sol está bajo el horizonte al anochecer. La precisión con la que los insectos pueden orientarse utilizando patrones de polarización nocturna es todavía un tema de estudio. Hasta ahora, se sabe que los grillos nocturnos tienen sensores de polarización de campo amplio y deberían poder utilizar los patrones de polarización nocturnos para orientarse. También se ha visto que las aves migratorias nocturnas se desorientan cuando el patrón de polarización al anochecer no es claro.
El mejor ejemplo es la abeja halicítida Megalopta genalis , que habita en las selvas tropicales de América Central y busca comida antes del amanecer y después del atardecer. Esta abeja abandona su nido aproximadamente una hora antes del amanecer, busca comida durante hasta 30 minutos y regresa a su nido con precisión antes del amanecer. Actúa de manera similar justo después del atardecer.
Por lo tanto, esta abeja es un ejemplo de un insecto que puede percibir patrones de polarización durante el crepúsculo astronómico. [3] Este caso no solo ejemplifica el hecho de que los patrones de polarización están presentes durante el crepúsculo, sino que sigue siendo un ejemplo perfecto de que cuando las condiciones de luz son desafiantes, la abeja se orienta en función de los patrones de polarización del cielo crepuscular.
Se ha sugerido que los vikingos podían navegar en mar abierto de manera similar, utilizando el cristal birrefringente espato de Islandia , al que llamaban "piedra solar", para determinar la orientación de la polarización del cielo. [4] [5] [6] [7] [8] Esto permitiría al navegante localizar el Sol, incluso cuando estaba oculto por una capa de nubes. Un ejemplo real de una "piedra solar" de este tipo se encontró en un barco hundido (Tudor) fechado en 1592, cerca del equipo de navegación del barco. [9]
Tanto los objetos artificiales como los naturales del cielo pueden ser muy difíciles de detectar utilizando únicamente la intensidad de la luz. Estos objetos incluyen nubes, satélites y aeronaves. Sin embargo, la polarización de estos objetos debido a la dispersión resonante , la emisión , la reflexión u otros fenómenos puede diferir de la de la iluminación de fondo. Por lo tanto, se pueden detectar más fácilmente utilizando imágenes de polarización. Existe una amplia gama de aplicaciones de teledetección en las que la polarización es útil para detectar objetos que de otro modo serían difíciles de ver.