En matemáticas , un polígono construible es un polígono regular que se puede construir con regla y compás . Por ejemplo, un pentágono regular se puede construir con regla y compás, mientras que un heptágono regular no. Hay una cantidad infinita de polígonos construibles, pero solo se conocen 31 con un número impar de lados.

Algunos polígonos regulares son fáciles de construir con compás y regla; otros no. Los antiguos matemáticos griegos sabían cómo construir un polígono regular con 3, 4 o 5 lados, [1] : p. xi y sabían cómo construir un polígono regular con el doble del número de lados de un polígono regular dado. [1] : pp. 49–50 Esto llevó a plantear la pregunta: ¿es posible construir todos los polígonos regulares con compás y regla? Si no, ¿cuáles n -gonos (es decir, polígonos con n aristas) son construibles y cuáles no?
Carl Friedrich Gauss demostró la constructibilidad del polígono regular de 17 polígonos en 1796. Cinco años después, desarrolló la teoría de los periodos gaussianos en sus Disquisitiones Arithmeticae . Esta teoría le permitió formular una condición suficiente para la constructibilidad de los polígonos regulares. Gauss afirmó sin prueba que esta condición también era necesaria , [2] pero nunca publicó su prueba.
En 1837, Pierre Wantzel dio una prueba completa de la necesidad. El resultado se conoce como el teorema de Gauss-Wantzel : un n -gono regular se puede construir con compás y regla si y solo si n es el producto de una potencia de 2 y cualquier número de primos de Fermat distintos (desiguales) . Aquí, una potencia de 2 es un número de la forma , donde m ≥ 0 es un entero. Un primo de Fermat es un número primo de la forma , donde m ≥ 0 es un entero. El número de primos de Fermat involucrados puede ser 0, en cuyo caso n es una potencia de 2.
Para reducir un problema geométrico a un problema de teoría de números pura , la prueba utiliza el hecho de que un n -gono regular es construible si y solo si el coseno es un número construible —es decir, puede escribirse en términos de las cuatro operaciones aritméticas básicas y la extracción de raíces cuadradas— . De manera equivalente, un n -gono regular es construible si cualquier raíz del n- ésimo polinomio ciclotómico es construible.
Reformulando el teorema de Gauss-Wantzel:
Los cinco primos de Fermat conocidos son:
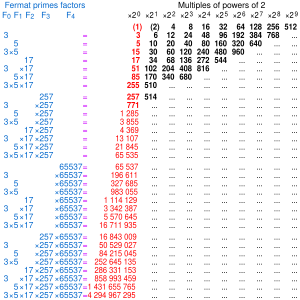
Dado que hay 31 subconjuntos no vacíos de los cinco primos de Fermat conocidos, hay 31 polígonos construibles conocidos con un número impar de lados.
Se sabe que los siguientes veintiocho números de Fermat, F 5 a F 32 , son compuestos . [3]
Por lo tanto, un n -gono regular es construible si
mientras que un n -gono regular no es construible con compás y regla si
Como hay cinco primos de Fermat conocidos, conocemos 31 números que son productos de primos de Fermat distintos y, por lo tanto, 31 polígonos regulares de lados impares construibles. Estos son 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611 , 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 (secuencia A045544 en la OEIS ). Como comentó John Conway en El libro de los números , estos números, cuando se escriben en binario , son iguales a las primeras 32 filas del triángulo de Pascal módulo -2 , menos la fila superior, que corresponde a un monógono . (Debido a esto, los 1 en dicha lista forman una aproximación al triángulo de Sierpiński ). Este patrón se rompe después de esto, ya que el siguiente número de Fermat es compuesto (4294967297 = 641 × 6700417), por lo que las siguientes filas no corresponden a polígonos construibles. Se desconoce si existen más primos de Fermat y, por lo tanto, se desconoce cuántos polígonos regulares construibles de lados impares existen. En general, si hay q primos de Fermat, entonces hay 2 q −1 polígonos regulares construibles de lados impares .
A la luz de trabajos posteriores sobre la teoría de Galois , se han aclarado los principios de estas demostraciones. Es sencillo demostrar a partir de la geometría analítica que las longitudes construibles deben provenir de longitudes base mediante la solución de alguna secuencia de ecuaciones cuadráticas . [4] En términos de la teoría de campos , dichas longitudes deben estar contenidas en una extensión de campo generada por una torre de extensiones cuadráticas . De ello se deduce que un campo generado por construcciones siempre tendrá grado sobre el campo base que es una potencia de dos.
En el caso específico de un n -gono regular, la cuestión se reduce a la cuestión de construir una longitud
que es un número trigonométrico y, por lo tanto, un número algebraico . Este número se encuentra en el n -ésimo cuerpo ciclotómico —y, de hecho, en su subcuerpo real , que es un cuerpo totalmente real y un espacio vectorial racional de dimensión
donde φ( n ) es la función totiente de Euler . El resultado de Wantzel se reduce a un cálculo que muestra que φ( n ) es una potencia de 2 precisamente en los casos especificados.
En cuanto a la construcción de Gauss, cuando el grupo de Galois es un 2-grupo se deduce que tiene una secuencia de subgrupos de órdenes
que están anidados, cada uno en el siguiente (una serie de composición , en la terminología de la teoría de grupos ), algo simple de demostrar por inducción en este caso de un grupo abeliano . Por lo tanto, hay subcuerpos anidados dentro del cuerpo ciclotómico, cada uno de grado 2 sobre el anterior. Los generadores para cada uno de esos cuerpos se pueden escribir mediante la teoría de períodos de Gauss . Por ejemplo, para n = 17 hay un período que es una suma de ocho raíces de la unidad , uno que es una suma de cuatro raíces de la unidad y uno que es la suma de dos, que es
Cada una de ellas es una raíz de una ecuación cuadrática en función de la ecuación anterior. Además, estas ecuaciones tienen raíces reales en lugar de complejas , por lo que en principio pueden resolverse mediante una construcción geométrica: esto se debe a que todo el trabajo se realiza dentro de un campo totalmente real.
De esta manera el resultado de Gauss puede ser entendido en términos actuales; para el cálculo real de las ecuaciones a resolver, los periodos pueden ser elevados al cuadrado y comparados con los periodos 'inferiores', en un algoritmo bastante factible.
Se conocen construcciones con regla y compás para todos los polígonos construibles conocidos. Si n = pq con p = 2 o p y q son coprimos , se puede construir un n -gono a partir de un p -gono y un q -gono.
Por lo tanto, sólo hay que encontrar una construcción con regla y compás para n -gonos donde n es un primo de Fermat.


De izquierda a derecha, construcciones de un 15-gono , 17-gono , 257-gono y 65537-gono . Solo se muestra la primera etapa de la construcción de 65537-gono; las construcciones de los 15-gonos, 17-gonos y 257-gonos se dan completas.
El concepto de constructibilidad que se analiza en este artículo se aplica específicamente a las construcciones con regla y compás . Si se permiten otras herramientas, se pueden realizar más construcciones. Las llamadas construcciones de neusis , por ejemplo, utilizan una regla marcada . Las construcciones son una idealización matemática y se supone que se realizan con exactitud.
Un polígono regular con n lados se puede construir con regla, compás y trisectriz de ángulos si y solo si donde r, s, k ≥ 0 y donde los p i son primos de Pierpont distintos mayores que 3 (primos de la forma [8] : Teoría 2 Estos polígonos son exactamente los polígonos regulares que se pueden construir con Sección cónica , y los polígonos regulares que se pueden construir con Plegado de papel . Los primeros números de lados de estos polígonos son: