stringtranslate.com

Predicción numérica del tiempo

Se muestra una cuadrícula para un modelo numérico del clima. La cuadrícula divide la superficie de la Tierra a lo largo de meridianos y paralelos, y simula el espesor de la atmósfera apilando celdas de la cuadrícula alejándolas del centro de la Tierra. Un recuadro muestra los diferentes procesos físicos analizados en cada celda de la cuadrícula, como la advección, la precipitación, la radiación solar y el enfriamiento radiativo terrestre.
Los modelos meteorológicos utilizan sistemas de ecuaciones diferenciales basados ​​en las leyes de la física , que detallan el movimiento de fluidos , la termodinámica , la transferencia radiativa y la química , y utilizan un sistema de coordenadas que divide el planeta en una cuadrícula 3D. Los vientos , la transferencia de calor , la radiación solar , la humedad relativa , los cambios de fase del agua y la hidrología de la superficie se calculan dentro de cada celda de la cuadrícula, y las interacciones con las celdas vecinas se utilizan para calcular las propiedades atmosféricas en el futuro.

La predicción numérica del tiempo ( NWP ) utiliza modelos matemáticos de la atmósfera y los océanos para predecir el tiempo basándose en las condiciones meteorológicas actuales. Aunque se intentó por primera vez en la década de 1920, no fue hasta la llegada de la simulación por ordenador en la década de 1950 que las predicciones numéricas del tiempo produjeron resultados realistas. En diferentes países del mundo se ejecutan varios modelos de pronóstico globales y regionales que utilizan como entrada las observaciones meteorológicas actuales transmitidas por radiosondas , satélites meteorológicos y otros sistemas de observación.

Los modelos matemáticos basados ​​en los mismos principios físicos se pueden utilizar para generar pronósticos meteorológicos a corto plazo o predicciones climáticas a largo plazo; estas últimas se aplican ampliamente para comprender y proyectar el cambio climático . Las mejoras realizadas en los modelos regionales han permitido mejoras significativas en los pronósticos de la trayectoria de los ciclones tropicales y de la calidad del aire ; sin embargo, los modelos atmosféricos funcionan mal a la hora de manejar procesos que ocurren en un área relativamente restringida, como los incendios forestales .

Para manipular los grandes conjuntos de datos y realizar los complejos cálculos necesarios para la predicción numérica moderna del tiempo se necesitan algunas de las supercomputadoras más potentes del mundo. Incluso con la creciente potencia de las supercomputadoras, la capacidad de predicción de los modelos numéricos del tiempo se extiende a sólo unos seis días. Los factores que afectan a la precisión de las predicciones numéricas incluyen la densidad y la calidad de las observaciones utilizadas como entrada para las predicciones, junto con las deficiencias en los propios modelos numéricos. Se han desarrollado técnicas de posprocesamiento como las estadísticas de salida del modelo (MOS) para mejorar el manejo de los errores en las predicciones numéricas.

Un problema más fundamental radica en la naturaleza caótica de las ecuaciones diferenciales parciales que describen la atmósfera. Es imposible resolver estas ecuaciones con exactitud, y los pequeños errores aumentan con el tiempo (duplicándose aproximadamente cada cinco días). La comprensión actual es que este comportamiento caótico limita los pronósticos precisos a unos 14 días, incluso con datos de entrada precisos y un modelo perfecto. Además, las ecuaciones diferenciales parciales utilizadas en el modelo deben complementarse con parametrizaciones para la radiación solar , los procesos húmedos (nubes y precipitación ), el intercambio de calor , el suelo, la vegetación, el agua superficial y los efectos del terreno. En un esfuerzo por cuantificar la gran cantidad de incertidumbre inherente que permanece en las predicciones numéricas, los pronósticos de conjunto se han utilizado desde la década de 1990 para ayudar a medir la confianza en el pronóstico y obtener resultados útiles más lejanos en el futuro de lo que sería posible de otra manera. Este enfoque analiza múltiples pronósticos creados con un modelo de pronóstico individual o múltiples modelos.

Historia

El panel de control principal de ENIAC en la Escuela Moore de Ingeniería Eléctrica operado por Betty Jennings y Frances Bilas

La historia de la predicción numérica del tiempo comenzó en la década de 1920 gracias a los esfuerzos de Lewis Fry Richardson , quien utilizó procedimientos desarrollados originalmente por Vilhelm Bjerknes [1] para producir a mano un pronóstico de seis horas del estado de la atmósfera en dos puntos de Europa central, tardando al menos seis semanas en hacerlo. [2] [1] [3] No fue hasta la llegada de la computadora y las simulaciones por computadora que el tiempo de cálculo se redujo a menos del período de pronóstico en sí. El ENIAC se utilizó para crear los primeros pronósticos meteorológicos por computadora en 1950, basados ​​​​en una aproximación altamente simplificada a las ecuaciones que gobiernan la atmósfera. [4] [5] En 1954, el grupo de Carl-Gustav Rossby en el Instituto Meteorológico e Hidrológico Sueco utilizó el mismo modelo para producir el primer pronóstico operativo (es decir, una predicción de rutina para uso práctico). [6] La predicción numérica operacional del tiempo en los Estados Unidos comenzó en 1955 bajo la Unidad Conjunta de Predicción Numérica del Tiempo (JNWPU), un proyecto conjunto de la Fuerza Aérea , la Armada y la Oficina Meteorológica de los Estados Unidos . [7] En 1956, Norman Phillips desarrolló un modelo matemático que podía representar de manera realista los patrones mensuales y estacionales en la troposfera; este se convirtió en el primer modelo climático exitoso . [8] [9] Después del trabajo de Phillips, varios grupos comenzaron a trabajar para crear modelos de circulación general . [10] El primer modelo climático de circulación general que combinaba procesos oceánicos y atmosféricos se desarrolló a fines de la década de 1960 en el Laboratorio de Dinámica de Fluidos Geofísicos de la NOAA . [11]

A medida que las computadoras se han vuelto más poderosas, el tamaño de los conjuntos de datos iniciales ha aumentado y se han desarrollado modelos atmosféricos más nuevos para aprovechar la potencia computacional adicional disponible. Estos modelos más nuevos incluyen más procesos físicos en las simplificaciones de las ecuaciones de movimiento en simulaciones numéricas de la atmósfera. [6] En 1966, Alemania Occidental y los Estados Unidos comenzaron a producir pronósticos operativos basados ​​en modelos de ecuaciones primitivas , seguidos por el Reino Unido en 1972 y Australia en 1977. [1] [12] El desarrollo de modelos de área limitada (regionales) facilitó avances en el pronóstico de las trayectorias de los ciclones tropicales , así como de la calidad del aire en los años 1970 y 1980. [13] [14] A principios de la década de 1980, los modelos comenzaron a incluir las interacciones del suelo y la vegetación con la atmósfera, lo que llevó a pronósticos más realistas. [15]

Los resultados de los modelos de predicción basados ​​en la dinámica atmosférica no permiten resolver algunos detalles del clima cerca de la superficie de la Tierra. Por ello, en los años 1970 y 1980 se desarrolló una relación estadística entre los resultados de un modelo meteorológico numérico y las condiciones resultantes en el terreno, conocida como estadísticas de resultados de modelos (MOS). [16] [17] A partir de los años 1990, se han utilizado pronósticos de conjuntos de modelos para ayudar a definir la incertidumbre de los pronósticos y ampliar el período en el que los pronósticos numéricos del clima son viables más allá de lo que sería posible de otro modo. [18] [19] [20]

Inicialización

Un avión de reconocimiento meteorológico WP-3D Orion en vuelo.
Los aviones de reconocimiento meteorológico, como este WP-3D Orion , proporcionan datos que luego se utilizan en pronósticos meteorológicos numéricos.

La atmósfera es un fluido . Como tal, la idea de la predicción numérica del tiempo es tomar muestras del estado del fluido en un momento dado y usar las ecuaciones de la dinámica de fluidos y la termodinámica para estimar el estado del fluido en algún momento en el futuro. El proceso de ingresar datos de observación en el modelo para generar condiciones iniciales se llama inicialización . En tierra, los mapas de terreno disponibles en resoluciones de hasta 1 kilómetro (0,6 mi) a nivel mundial se utilizan para ayudar a modelar las circulaciones atmosféricas dentro de regiones de topografía accidentada, con el fin de representar mejor características como vientos descendentes, ondas de montaña y nubosidad relacionada que afecta la radiación solar entrante. [21] Las principales entradas de los servicios meteorológicos de los países son observaciones de dispositivos (llamados radiosondas ) en globos meteorológicos que miden varios parámetros atmosféricos y los transmiten a un receptor fijo, así como de satélites meteorológicos . La Organización Meteorológica Mundial actúa para estandarizar la instrumentación, las prácticas de observación y el tiempo de estas observaciones en todo el mundo. Las estaciones informan cada hora en informes METAR , [22] o cada seis horas en informes SYNOP . [23] Estas observaciones están espaciadas irregularmente, por lo que son procesadas mediante métodos de asimilación de datos y análisis objetivo, que realizan un control de calidad y obtienen valores en ubicaciones utilizables por los algoritmos matemáticos del modelo. [24] Los datos luego se utilizan en el modelo como punto de partida para un pronóstico. [25]

Se utilizan diversos métodos para reunir datos de observación para su uso en modelos numéricos. Los sitios lanzan radiosondas en globos meteorológicos que se elevan a través de la troposfera y hasta la estratosfera . [26] La información de los satélites meteorológicos se utiliza donde no se dispone de fuentes de datos tradicionales. Commerce proporciona informes de pilotos a lo largo de las rutas de las aeronaves [27] e informes de barcos a lo largo de las rutas de navegación. [28] Los proyectos de investigación utilizan aviones de reconocimiento para volar dentro y alrededor de los sistemas meteorológicos de interés, como los ciclones tropicales . [29] [30] Los aviones de reconocimiento también vuelan sobre los océanos abiertos durante la temporada fría en sistemas que causan una incertidumbre significativa en la guía de pronóstico, o se espera que tengan un alto impacto de tres a siete días en el futuro sobre el continente río abajo. [31] El hielo marino comenzó a inicializarse en los modelos de pronóstico en 1971. [32] Los esfuerzos para involucrar la temperatura de la superficie del mar en la inicialización del modelo comenzaron en 1972 debido a su papel en la modulación del clima en latitudes más altas del Pacífico. [33]

Cálculo

Un gráfico de pronóstico del pronóstico de 96 horas de altura geopotencial de 850 mbar y temperatura del Sistema de pronóstico global

Un modelo atmosférico es un programa informático que produce información meteorológica para tiempos futuros en lugares y altitudes determinados. Dentro de cualquier modelo moderno hay un conjunto de ecuaciones, conocidas como ecuaciones primitivas , que se utilizan para predecir el estado futuro de la atmósfera. [34] Estas ecuaciones, junto con la ley de los gases ideales , se utilizan para desarrollar los campos escalares de densidad , presión y temperatura potencial y el campo vectorial de velocidad del aire (viento) de la atmósfera a través del tiempo. También se incluyen ecuaciones de transporte adicionales para contaminantes y otros aerosoles en algunos modelos de alta resolución de ecuaciones primitivas. [35] Las ecuaciones utilizadas son ecuaciones diferenciales parciales no lineales que son imposibles de resolver exactamente a través de métodos analíticos, [36] con la excepción de unos pocos casos idealizados. [37] Por lo tanto, los métodos numéricos obtienen soluciones aproximadas. Diferentes modelos utilizan diferentes métodos de solución: algunos modelos globales y casi todos los modelos regionales utilizan métodos de diferencias finitas para las tres dimensiones espaciales, mientras que otros modelos globales y algunos modelos regionales utilizan métodos espectrales para las dimensiones horizontales y métodos de diferencias finitas en la vertical. [36]

Estas ecuaciones se inicializan a partir de los datos de análisis y se determinan las tasas de cambio. Estas tasas de cambio predicen el estado de la atmósfera en un corto tiempo en el futuro; el incremento de tiempo para esta predicción se llama paso de tiempo . Este estado atmosférico futuro se utiliza luego como punto de partida para otra aplicación de las ecuaciones predictivas para encontrar nuevas tasas de cambio, y estas nuevas tasas de cambio predicen la atmósfera en un paso de tiempo aún más en el futuro. Este paso de tiempo se repite hasta que la solución alcanza el tiempo de pronóstico deseado. La longitud del paso de tiempo elegido dentro del modelo está relacionada con la distancia entre los puntos en la cuadrícula computacional y se elige para mantener la estabilidad numérica . [38] Los pasos de tiempo para los modelos globales son del orden de decenas de minutos, [39] mientras que los pasos de tiempo para los modelos regionales son entre uno y cuatro minutos. [40] Los modelos globales se ejecutan en diferentes momentos en el futuro. El modelo unificado de UKMET se ejecuta seis días en el futuro, [41] mientras que el Sistema de pronóstico integrado del Centro europeo de pronósticos meteorológicos a medio plazo y el Modelo multiescala ambiental global de Environment Canada se ejecutan hasta diez días en el futuro, [42] y el modelo del Sistema de pronóstico global ejecutado por el Centro de modelado ambiental se ejecuta dieciséis días en el futuro. [43] La salida visual producida por una solución de modelo se conoce como un gráfico de pronóstico o prog . [44]

Parametrización

Campo de nubes cúmulos , que están parametrizadas porque son demasiado pequeñas para ser incluidas explícitamente en la predicción numérica del tiempo.

Algunos procesos meteorológicos son demasiado pequeños o demasiado complejos para incluirlos explícitamente en los modelos numéricos de predicción del tiempo. La parametrización es un procedimiento para representar estos procesos relacionándolos con variables en las escalas que resuelve el modelo. Por ejemplo, las cuadrículas de los modelos meteorológicos y climáticos tienen lados de entre 5 y 300 kilómetros de longitud. Un cúmulo típico tiene una escala de menos de 1 kilómetro y requeriría una cuadrícula aún más fina para ser representada físicamente por las ecuaciones del movimiento de fluidos. Por lo tanto, los procesos que representan dichas nubes están parametrizados mediante procesos de diversa sofisticación. En los primeros modelos, si una columna de aire dentro de una cuadrícula del modelo era condicionalmente inestable (esencialmente, la parte inferior era más cálida y húmeda que la superior) y el contenido de vapor de agua en cualquier punto dentro de la columna se saturaba, entonces se volcaba (el aire cálido y húmedo comenzaba a ascender) y el aire en esa columna vertical se mezclaba. Los esquemas más sofisticados reconocen que sólo algunas porciones de la caja pueden conveccionarse y que se producen arrastre y otros procesos. Los modelos meteorológicos que tienen cajas de cuadrícula con tamaños entre 5 y 25 kilómetros (3 y 16 millas) pueden representar explícitamente las nubes convectivas, aunque necesitan parametrizar la microfísica de las nubes que se produce a una escala menor. [45] La formación de nubes a gran escala ( tipo estratos ) tiene una base más física; se forman cuando la humedad relativa alcanza un valor prescrito. La fracción de nubes se puede relacionar con este valor crítico de humedad relativa. [46]

La cantidad de radiación solar que llega al suelo, así como la formación de gotitas de nubes, ocurren a escala molecular, por lo que deben parametrizarse antes de que puedan incluirse en el modelo. El arrastre atmosférico producido por las montañas también debe parametrizarse, ya que las limitaciones en la resolución de los contornos de elevación producen subestimaciones significativas del arrastre. [47] Este método de parametrización también se realiza para el flujo de energía superficial entre el océano y la atmósfera, con el fin de determinar temperaturas realistas de la superficie del mar y el tipo de hielo marino que se encuentra cerca de la superficie del océano. [48] Se tiene en cuenta el ángulo del sol, así como el impacto de múltiples capas de nubes. [49] El tipo de suelo, el tipo de vegetación y la humedad del suelo determinan cuánta radiación entra en el calentamiento y cuánta humedad se absorbe en la atmósfera adyacente, por lo que es importante parametrizar su contribución a estos procesos. [50] Dentro de los modelos de calidad del aire, las parametrizaciones tienen en cuenta las emisiones atmosféricas de múltiples fuentes relativamente pequeñas (por ejemplo, carreteras, campos, fábricas) dentro de casillas de cuadrícula específicas. [51]

Dominios

Se muestra un sistema de coordenadas sigma. Las líneas de valores sigma iguales siguen el terreno en la parte inferior y se suavizan gradualmente hacia la parte superior de la atmósfera.
Sección transversal de la atmósfera sobre el terreno con una representación en coordenadas sigma. Los modelos de mesoescala dividen la atmósfera verticalmente utilizando representaciones similares a la que se muestra aquí.

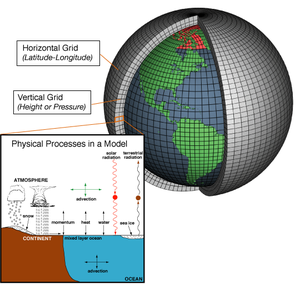
El dominio horizontal de un modelo es global , cubriendo toda la Tierra, o regional , cubriendo solo una parte de ella. Los modelos regionales (también conocidos como modelos de área limitada o LAM) permiten el uso de un espaciado de cuadrícula más fino que los modelos globales porque los recursos computacionales disponibles se concentran en un área específica en lugar de estar esparcidos por todo el globo. Esto permite que los modelos regionales resuelvan explícitamente fenómenos meteorológicos de escala más pequeña que no se pueden representar en la cuadrícula más gruesa de un modelo global. Los modelos regionales utilizan un modelo global para especificar las condiciones en el borde de su dominio ( condiciones de contorno ) para permitir que los sistemas de fuera del dominio del modelo regional se muevan hacia su área. La incertidumbre y los errores dentro de los modelos regionales son introducidos por el modelo global utilizado para las condiciones de contorno del borde del modelo regional, así como los errores atribuibles al propio modelo regional. [52]

Un gráfico del tamaño del dominio del modelo versus el tamaño de la cuadrícula del modelo con varios tipos diferentes de modelos numéricos dispuestos en diagonal.
Una comparación de diferentes tipos de modelos atmosféricos por dominio espacial y tamaño de la cuadrícula del modelo.

La coordenada vertical se maneja de varias maneras. El modelo de Lewis Fry Richardson de 1922 utilizó la altura geométrica ( ) como coordenada vertical. Los modelos posteriores sustituyeron la coordenada geométrica por un sistema de coordenadas de presión, en el que las alturas geopotenciales de las superficies de presión constante se convierten en variables dependientes , simplificando enormemente las ecuaciones primitivas. [53] Esta correlación entre sistemas de coordenadas se puede realizar ya que la presión disminuye con la altura a través de la atmósfera de la Tierra . [54] El primer modelo utilizado para pronósticos operativos, el modelo barotrópico de una sola capa, utilizó una sola coordenada de presión en el nivel de 500 milibares (aproximadamente 5500 m (18 000 pies)), [4] y, por lo tanto, era esencialmente bidimensional. Los modelos de alta resolución, también llamados modelos de mesoescala , como el modelo Weather Research and Forecasting tienden a utilizar coordenadas de presión normalizadas denominadas coordenadas sigma . [55] Este sistema de coordenadas recibe su nombre de la variable independiente utilizada para escalar las presiones atmosféricas con respecto a la presión en la superficie, y en algunos casos también con la presión en la parte superior del dominio. [56]


Estadísticas de salida del modelo

Debido a que los modelos de pronóstico basados ​​en las ecuaciones de la dinámica atmosférica no determinan perfectamente las condiciones meteorológicas, se han desarrollado métodos estadísticos para intentar corregir los pronósticos. Se crearon modelos estadísticos basados ​​en los campos tridimensionales producidos por los modelos meteorológicos numéricos, las observaciones de superficie y las condiciones climatológicas para lugares específicos. Estos modelos estadísticos se conocen colectivamente como estadísticas de salida del modelo (MOS), [57] y fueron desarrollados por el Servicio Meteorológico Nacional para su conjunto de modelos de pronóstico del tiempo a fines de la década de 1960. [16] [58]

Las estadísticas de salida del modelo difieren de la técnica de prog perfecto , que supone que la salida de la guía de predicción numérica del tiempo es perfecta. [59] MOS puede corregir los efectos locales que no pueden ser resueltos por el modelo debido a una resolución de cuadrícula insuficiente, así como los sesgos del modelo. Debido a que MOS se ejecuta después de su respectivo modelo global o regional, su producción se conoce como posprocesamiento. Los parámetros de pronóstico dentro de MOS incluyen temperaturas máximas y mínimas, probabilidad porcentual de lluvia dentro de un período de varias horas, cantidad de precipitación esperada, probabilidad de que la precipitación sea de naturaleza congelada, probabilidad de tormentas eléctricas, nubosidad y vientos superficiales. [60]

Conjuntos

Se muestran dos imágenes. La imagen superior muestra tres posibles trayectorias que podría haber seguido el huracán Rita. Los contornos sobre la costa de Texas corresponden a la presión atmosférica a nivel del mar prevista al pasar la tormenta. La imagen inferior muestra un conjunto de pronósticos de trayectoria elaborados por diferentes modelos meteorológicos para el mismo huracán.
Arriba : Simulación del modelo de investigación y pronóstico del tiempo (WRF) de las trayectorias del huracán Rita (2005). Abajo : Dispersión del pronóstico del conjunto multimodelo del NHC.

En 1963, Edward Lorenz descubrió la naturaleza caótica de las ecuaciones de dinámica de fluidos involucradas en la predicción meteorológica. [61] Los errores extremadamente pequeños en temperatura, vientos u otros datos iniciales dados a los modelos numéricos se amplificarán y duplicarán cada cinco días, [61] haciendo imposible que los pronósticos de largo plazo (aquellos realizados con más de dos semanas de anticipación) predigan el estado de la atmósfera con algún grado de habilidad de pronóstico . Además, las redes de observación existentes tienen una cobertura deficiente en algunas regiones (por ejemplo, sobre grandes masas de agua como el Océano Pacífico), lo que introduce incertidumbre en el verdadero estado inicial de la atmósfera. Si bien existe un conjunto de ecuaciones, conocidas como ecuaciones de Liouville , para determinar la incertidumbre inicial en la inicialización del modelo, las ecuaciones son demasiado complejas para ejecutarlas en tiempo real, incluso con el uso de supercomputadoras. [62] Estas incertidumbres limitan la precisión del modelo de pronóstico a aproximadamente cinco o seis días en el futuro. [63] [64]

Edward Epstein reconoció en 1969 que la atmósfera no podía describirse completamente con una única ejecución de pronóstico debido a la incertidumbre inherente, y propuso utilizar un conjunto de simulaciones estocásticas de Monte Carlo para producir medias y varianzas para el estado de la atmósfera. [65] Aunque este primer ejemplo de un conjunto mostró habilidad, en 1974 Cecil Leith demostró que producían pronósticos adecuados solo cuando la distribución de probabilidad del conjunto era una muestra representativa de la distribución de probabilidad en la atmósfera. [66]

Desde la década de 1990, los pronósticos de conjunto se han utilizado operativamente (como pronósticos de rutina) para dar cuenta de la naturaleza estocástica de los procesos meteorológicos, es decir, para resolver su incertidumbre inherente. Este método implica analizar múltiples pronósticos creados con un modelo de pronóstico individual utilizando diferentes parametrizaciones físicas o variando las condiciones iniciales. [62] A partir de 1992 con los pronósticos de conjunto preparados por el Centro Europeo de Pronósticos Meteorológicos de Plazo Medio (ECMWF) y los Centros Nacionales de Predicción Ambiental , los pronósticos de conjunto de modelos se han utilizado para ayudar a definir la incertidumbre del pronóstico y para extender la ventana en la que el pronóstico numérico del tiempo es viable más lejos en el futuro de lo que sería posible de otra manera. [18] [19] [20] El modelo ECMWF, el Sistema de Predicción de Conjuntos, [19] utiliza vectores singulares para simular la densidad de probabilidad inicial , mientras que el conjunto NCEP, el Sistema de Pronóstico de Conjuntos Globales, utiliza una técnica conocida como cría de vectores . [18] [20] La Oficina Meteorológica del Reino Unido ejecuta pronósticos de conjunto globales y regionales donde las perturbaciones de las condiciones iniciales son utilizadas por 24 miembros del conjunto en el Sistema de Predicción de Conjunto Global y Regional de la Oficina Meteorológica (MOGREPS) para producir 24 pronósticos diferentes. [67]

En un enfoque basado en un solo modelo, el pronóstico del conjunto generalmente se evalúa en términos de un promedio de los pronósticos individuales con respecto a una variable de pronóstico, así como el grado de acuerdo entre varios pronósticos dentro del sistema de conjunto, como se representa por su dispersión general. La dispersión del conjunto se diagnostica a través de herramientas como los diagramas de espagueti , que muestran la dispersión de una cantidad en los gráficos de pronóstico para pasos de tiempo específicos en el futuro. Otra herramienta donde se utiliza la dispersión del conjunto es un meteograma , que muestra la dispersión en el pronóstico de una cantidad para una ubicación específica. Es común que la dispersión del conjunto sea demasiado pequeña para incluir el clima que realmente ocurre, lo que puede llevar a los pronosticadores a diagnosticar erróneamente la incertidumbre del modelo; [68] este problema se vuelve particularmente grave para los pronósticos del clima con unos diez días de anticipación. [69] Cuando la dispersión del conjunto es pequeña y las soluciones de pronóstico son consistentes dentro de múltiples ejecuciones del modelo, los pronosticadores perciben más confianza en la media del conjunto y el pronóstico en general. [68] A pesar de esta percepción, la relación entre dispersión y habilidad de pronóstico es a menudo débil o no se encuentra, ya que las correlaciones dispersión-error normalmente son menores a 0,6, y solo en circunstancias especiales varían entre 0,6 y 0,7. [70] La relación entre dispersión de conjunto y habilidad de pronóstico varía sustancialmente dependiendo de factores tales como el modelo de pronóstico y la región para la cual se realiza el pronóstico. [ cita requerida ]

De la misma manera que se pueden utilizar muchos pronósticos de un solo modelo para formar un conjunto, también se pueden combinar varios modelos para producir un pronóstico de conjunto. Este enfoque se denomina pronóstico de conjunto de múltiples modelos y se ha demostrado que mejora los pronósticos en comparación con un enfoque basado en un solo modelo. [71] Los modelos dentro de un conjunto de múltiples modelos se pueden ajustar para sus diversos sesgos, lo que es un proceso conocido como pronóstico de superconjunto . Este tipo de pronóstico reduce significativamente los errores en la salida del modelo. [72]

Aplicaciones

Modelado de la calidad del aire

Los pronósticos de la calidad del aire intentan predecir cuándo las concentraciones de contaminantes alcanzarán niveles que sean peligrosos para la salud pública. La concentración de contaminantes en la atmósfera está determinada por su transporte , o velocidad media de movimiento a través de la atmósfera, su difusión , transformación química y deposición en el suelo . [73] Además de la información sobre la fuente de contaminantes y el terreno, estos modelos requieren datos sobre el estado del flujo de fluidos en la atmósfera para determinar su transporte y difusión. [74] Las condiciones meteorológicas como las inversiones térmicas pueden evitar que el aire de la superficie se eleve, atrapando contaminantes cerca de la superficie, [75] lo que hace que los pronósticos precisos de tales eventos sean cruciales para el modelado de la calidad del aire. Los modelos de calidad del aire urbano requieren una malla computacional muy fina, lo que requiere el uso de modelos meteorológicos de mesoescala de alta resolución; a pesar de esto, la calidad de la guía meteorológica numérica es la principal incertidumbre en los pronósticos de la calidad del aire. [74]

Modelado climático

Un modelo de circulación general (GCM) es un modelo matemático que se puede utilizar en simulaciones por computadora de la circulación global de una atmósfera planetaria o un océano. Un modelo de circulación general atmosférica (AGCM) es esencialmente lo mismo que un modelo numérico global de predicción meteorológica, y algunos (como el utilizado en el Modelo Unificado del Reino Unido) se pueden configurar tanto para pronósticos meteorológicos a corto plazo como para predicciones climáticas a largo plazo. Junto con el hielo marino y los componentes de la superficie terrestre, los AGCM y los GCM oceánicos (OGCM) son componentes clave de los modelos climáticos globales y se aplican ampliamente para comprender el clima y proyectar el cambio climático . Para los aspectos del cambio climático, se puede introducir una variedad de escenarios de emisiones químicas creadas por el hombre en los modelos climáticos para ver cómo un efecto invernadero mejorado modificaría el clima de la Tierra. [76] Las versiones diseñadas para aplicaciones climáticas con escalas de tiempo de décadas a siglos fueron creadas originalmente en 1969 por Syukuro Manabe y Kirk Bryan en el Laboratorio de Dinámica de Fluidos Geofísicos en Princeton, Nueva Jersey . [77] Cuando se ejecutan durante varias décadas, las limitaciones computacionales significan que los modelos deben utilizar una cuadrícula gruesa que deja sin resolver las interacciones de menor escala. [78]

Modelado de la superficie oceánica

Pronóstico de viento y olas para el océano Atlántico Norte. Se identifican dos áreas de olas altas: una al oeste del extremo sur de Groenlandia y la otra en el mar del Norte. Se pronostica mar en calma para el golfo de México. Las barras de viento muestran las intensidades y direcciones esperadas del viento a intervalos regulares sobre el Atlántico Norte.
Pronóstico de viento y olas de 120 horas de NOAA Wavewatch III para el Atlántico Norte

La transferencia de energía entre el viento que sopla sobre la superficie de un océano y la capa superior del océano es un elemento importante en la dinámica de las olas. [79] La ecuación de transporte espectral de las olas se utiliza para describir el cambio en el espectro de las olas a medida que cambia la topografía. Simula la generación de olas, el movimiento de las olas (propagación dentro de un fluido), la reducción de las olas , la refracción , la transferencia de energía entre olas y la disipación de las olas. [80] Dado que los vientos superficiales son el principal mecanismo de fuerza en la ecuación de transporte espectral de las olas, los modelos de olas oceánicas utilizan la información producida por los modelos numéricos de predicción meteorológica como entradas para determinar cuánta energía se transfiere desde la atmósfera a la capa en la superficie del océano. Junto con la disipación de energía a través de crestas blancas y la resonancia entre olas, los vientos superficiales de los modelos numéricos meteorológicos permiten predicciones más precisas del estado de la superficie del mar. [81]

Pronóstico de ciclones tropicales

La predicción de ciclones tropicales también se basa en datos proporcionados por modelos numéricos del tiempo. Existen tres clases principales de modelos de orientación de ciclones tropicales : Los modelos estadísticos se basan en un análisis del comportamiento de las tormentas utilizando la climatología y correlacionan la posición y la fecha de una tormenta para producir un pronóstico que no se basa en la física de la atmósfera en ese momento. Los modelos dinámicos son modelos numéricos que resuelven las ecuaciones que gobiernan el flujo de fluidos en la atmósfera; se basan en los mismos principios que otros modelos numéricos de predicción del tiempo de área limitada, pero pueden incluir técnicas computacionales especiales, como dominios espaciales refinados que se mueven junto con el ciclón. Los modelos que utilizan elementos de ambos enfoques se denominan modelos estadístico-dinámicos. [82]

En 1978, comenzó a funcionar el primer modelo de seguimiento de huracanes basado en la dinámica atmosférica , el modelo de malla fina móvil (MFM). [13] En el campo de la predicción de la trayectoria de los ciclones tropicales , a pesar de la guía de modelos dinámicos en constante mejora que se produjo con el aumento de la potencia computacional, no fue hasta la década de 1980 cuando la predicción numérica del tiempo mostró su habilidad , y hasta la década de 1990 cuando superó consistentemente a los modelos estadísticos o dinámicos simples. [83] Las predicciones de la intensidad de un ciclón tropical basadas en la predicción numérica del tiempo siguen siendo un desafío, ya que los métodos estadísticos siguen mostrando una mayor habilidad que la guía dinámica. [84]

Modelado de incendios forestales

Un modelo sencillo de propagación de incendios forestales

A escala molecular, hay dos procesos de reacción principales que compiten en la degradación de la celulosa , o de los combustibles de madera, en los incendios forestales . Cuando hay una baja cantidad de humedad en una fibra de celulosa, se produce la volatilización del combustible; este proceso generará productos gaseosos intermedios que, en última instancia, serán la fuente de la combustión . Cuando hay humedad presente, o cuando se está alejando suficiente calor de la fibra, se produce la carbonización . La cinética química de ambas reacciones indica que hay un punto en el que el nivel de humedad es lo suficientemente bajo, y/o las tasas de calentamiento lo suficientemente altas, para que los procesos de combustión se vuelvan autosuficientes. En consecuencia, los cambios en la velocidad del viento, la dirección, la humedad, la temperatura o la tasa de gradiente térmico en diferentes niveles de la atmósfera pueden tener un impacto significativo en el comportamiento y el crecimiento de un incendio forestal. Dado que el incendio forestal actúa como una fuente de calor para el flujo atmosférico, el incendio forestal puede modificar los patrones de advección locales , introduciendo un bucle de retroalimentación entre el incendio y la atmósfera. [85]

Un modelo bidimensional simplificado para la propagación de incendios forestales que utilizó la convección para representar los efectos del viento y el terreno, así como la transferencia de calor radiativo como el método dominante de transporte de calor condujo a sistemas de reacción-difusión de ecuaciones diferenciales parciales . [86] [87] Los modelos más complejos unen modelos numéricos meteorológicos o modelos de dinámica de fluidos computacional con un componente de incendios forestales que permiten estimar los efectos de retroalimentación entre el incendio y la atmósfera. [85] La complejidad adicional en la última clase de modelos se traduce en un aumento correspondiente en sus requisitos de potencia de cómputo. De hecho, un tratamiento tridimensional completo de la combustión mediante simulación numérica directa a escalas relevantes para el modelado atmosférico no es práctico actualmente debido al excesivo costo computacional que requeriría tal simulación. Los modelos numéricos meteorológicos tienen una capacidad de pronóstico limitada en resoluciones espaciales inferiores a 1 kilómetro (0,6 mi), lo que obliga a los modelos complejos de incendios forestales a parametrizar el incendio para calcular cómo los vientos serán modificados localmente por el incendio forestal, y utilizar esos vientos modificados para determinar la velocidad a la que el incendio se propagará localmente. [88] [89] [90] Aunque modelos como FIRETEC de Los Álamos resuelven las concentraciones de combustible y oxígeno , la cuadrícula computacional no puede ser lo suficientemente fina para resolver la reacción de combustión, por lo que se deben hacer aproximaciones para la distribución de temperatura dentro de cada celda de la cuadrícula, así como para las tasas de reacción de combustión en sí. [ cita requerida ]

Véase también

Referencias

  1. ^ abc Lynch , Peter (marzo de 2008). "Los orígenes de la predicción meteorológica por ordenador y el modelado climático" (PDF) . Journal of Computational Physics . 227 (7): 3431–44. Bibcode :2008JCoPh.227.3431L. doi :10.1016/j.jcp.2007.02.034. Archivado desde el original (PDF) el 8 de julio de 2010. Consultado el 23 de diciembre de 2010 .
  2. ^ Simmons, AJ; Hollingsworth, A. (2002). "Algunos aspectos de la mejora en la habilidad de predicción numérica del tiempo". Quarterly Journal of the Royal Meteorological Society . 128 (580): 647–677. Bibcode :2002QJRMS.128..647S. doi :10.1256/003590002321042135. S2CID  121625425.
  3. ^ Lynch, Peter (2006). "Predicción meteorológica mediante procesos numéricos". El surgimiento de la predicción numérica del tiempo . Cambridge University Press . pp. 1–27. ISBN 978-0-521-85729-1.
  4. ^ ab Charney, Jule ; Fjørtoft, Ragnar ; von Neumann, John (noviembre de 1950). "Integración numérica de la ecuación de vorticidad barotrópica". Tellus . 2 (4): 237. Bibcode : 1950 Tell....2..237C. doi : 10.3402/tellusa.v2i4.8607 .
  5. ^ Cox, John D. (2002). Vigilantes de tormentas. John Wiley & Sons, Inc., pág. 208. ISBN 978-0-471-38108-2.
  6. ^ ab Harper, Kristine; Uccellini, Louis W.; Kalnay, Eugenia; Carey, Kenneth; Morone, Lauren (mayo de 2007). "2007: 50º aniversario de la predicción numérica operacional del tiempo". Boletín de la Sociedad Meteorológica Estadounidense . 88 (5): 639–650. Bibcode :2007BAMS...88..639H. doi : 10.1175/BAMS-88-5-639 .
  7. ^ Instituto Americano de Física (25 de marzo de 2008). «Modelado de la circulación general atmosférica». Archivado desde el original el 25 de marzo de 2008. Consultado el 13 de enero de 2008 .
  8. ^ Phillips, Norman A. (abril de 1956). "La circulación general de la atmósfera: un experimento numérico". Quarterly Journal of the Royal Meteorological Society . 82 (352): 123–154. Bibcode :1956QJRMS..82..123P. doi :10.1002/qj.49708235202.
  9. ^ Cox, John D. (2002). Vigilantes de tormentas. John Wiley & Sons, Inc., pág. 210. ISBN 978-0-471-38108-2.
  10. ^ Lynch, Peter (2006). "Las integraciones de ENIAC". El surgimiento de la predicción numérica del tiempo . Cambridge University Press . pp. 206–208. ISBN 978-0-521-85729-1.
  11. ^ Administración Nacional Oceánica y Atmosférica (22 de mayo de 2008). "El primer modelo climático" . Consultado el 8 de enero de 2011 .
  12. ^ Leslie, LM; Dietachmeyer, GS (diciembre de 1992). "Predicción numérica del tiempo en tiempo real para áreas limitadas en Australia: una perspectiva histórica" ​​(PDF) . Revista meteorológica australiana . 41 (SP): 61–77 . Consultado el 3 de enero de 2011 .
  13. ^ ab Shuman, Frederick G. (septiembre de 1989). "Historia de la predicción numérica del tiempo en el Centro Meteorológico Nacional". Tiempo y pronóstico . 4 (3): 286–296. Bibcode :1989WtFor...4..286S. doi : 10.1175/1520-0434(1989)004<0286:HONWPA>2.0.CO;2 .
  14. ^ Steyn, DG (1991). Modelado de la contaminación del aire y su aplicación VIII, Volumen 8. Birkhäuser. págs. 241–242. ISBN 978-0-306-43828-8.
  15. ^ Xue, Yongkang; Fennessey, Michael J. (20 de marzo de 1996). "Impacto de las propiedades de la vegetación en la predicción del clima de verano en Estados Unidos" (PDF) . Journal of Geophysical Research . 101 (D3): 7419. Bibcode :1996JGR...101.7419X. CiteSeerX 10.1.1.453.551 . doi :10.1029/95JD02169. Archivado desde el original (PDF) el 10 de julio de 2010 . Consultado el 6 de enero de 2011 . 
  16. ^ ab Hughes, Harry (1976). Guía de pronóstico de estadísticas de salida de modelos (PDF) . Centro de Aplicaciones Técnicas Ambientales de la Fuerza Aérea de los Estados Unidos. págs. 1–16. Archivado (PDF) desde el original el 17 de junio de 2019.
  17. ^ Best, DL; Pryor, SP (1983). Sistemas de estadísticas de salida del modelo del Servicio Meteorológico Aéreo . Air Force Global Weather Central. págs. 1–90.
  18. ^ abc Toth, Zoltan; Kalnay, Eugenia (diciembre de 1997). "Predicción por conjuntos en el NCEP y el método de crianza". Monthly Weather Review . 125 (12): 3297–3319. Bibcode :1997MWRv..125.3297T. ​​CiteSeerX 10.1.1.324.3941 . doi :10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2. S2CID  14668576. 
  19. ^ abc "El sistema de predicción de conjuntos (EPS)". ECMWF . Archivado desde el original el 2010-10-30 . Consultado el 2011-01-05 .
  20. ^ abc Molteni, F.; Buizza, R.; Palmer, TN ; Petroliagis, T. (enero de 1996). "El sistema de predicción por conjuntos del ECMWF: metodología y validación". Quarterly Journal of the Royal Meteorological Society . 122 (529): 73–119. Bibcode :1996QJRMS.122...73M. doi :10.1002/qj.49712252905.
  21. ^ Stensrud, David J. (2007). Esquemas de parametrización: claves para comprender los modelos numéricos de predicción meteorológica. Cambridge University Press. pág. 56. ISBN 978-0-521-86540-1.
  22. ^ Centro Nacional de Datos Climáticos (2008-08-20). «Key to METAR Surface Weather Observations» (Clave para las observaciones meteorológicas de superficie de METAR). Administración Nacional Oceánica y Atmosférica . Archivado desde el original el 2002-11-01 . Consultado el 2011-02-11 .
  23. ^ "Formato de datos SYNOP (FM-12): Observaciones sinópticas de superficie". UNISYS . 25 de mayo de 2008. Archivado desde el original el 30 de diciembre de 2007.
  24. ^ Krishnamurti, TN (enero de 1995). "Predicción numérica del tiempo". Revista anual de mecánica de fluidos . 27 (1): 195–225. Código Bibliográfico :1995AnRFM..27..195K. doi :10.1146/annurev.fl.27.010195.001211. S2CID  122230747.
  25. ^ "El sistema de asimilación de datos variacionales del WRF (WRF-Var)". University Corporation for Atmospheric Research . 14 de agosto de 2007. Archivado desde el original el 14 de agosto de 2007.
  26. ^ Gaffen, Dian J. (7 de junio de 2007). "Observaciones de radiosonda y su uso en investigaciones relacionadas con SPARC". Archivado desde el original el 7 de junio de 2007.
  27. ^ Ballish, Bradley A.; V. Krishna Kumar (noviembre de 2008). "Diferencias sistemáticas en las temperaturas de aeronaves y radiosonda" (PDF) . Boletín de la Sociedad Meteorológica Estadounidense . 89 (11): 1689–1708. Bibcode :2008BAMS...89.1689B. doi :10.1175/2008BAMS2332.1 . Consultado el 16 de febrero de 2011 .
  28. ^ National Data Buoy Center (28 de enero de 2009). "El plan de buques de observación voluntaria (VOS) de la OMM". Administración Nacional Oceánica y Atmosférica . Consultado el 15 de febrero de 2011 .
  29. ^ 403rd Wing (2011). "Los cazadores de huracanes". 53rd Weather Reconnaissance Squadron . Archivado desde el original el 2012-05-30 . Consultado el 2006-03-30 .{{cite web}}: CS1 maint: nombres numéricos: lista de autores ( enlace )
  30. ^ Lee, Christopher (8 de octubre de 2007). "Los drones y los sensores pueden abrir el camino hacia el ojo de la tormenta". The Washington Post . Consultado el 22 de febrero de 2008 .
  31. ^ Administración Nacional Oceánica y Atmosférica (12 de noviembre de 2010). "NOAA envía avión de investigación de alta tecnología para mejorar los pronósticos de tormentas invernales" . Consultado el 22 de diciembre de 2010 .
  32. ^ Stensrud, David J. (2007). Esquemas de parametrización: claves para entender los modelos numéricos de predicción meteorológica. Cambridge University Press . p. 137. ISBN 978-0-521-86540-1.
  33. ^ Houghton, John Theodore (1985). El clima global. Archivo de Cambridge University Press. Págs. 49-50. ISBN 978-0-521-31256-1.
  34. ^ Pielke, Roger A. (2002). Modelado meteorológico de mesoescala . Academic Press . Págs. 48-49. ISBN. 978-0-12-554766-6.
  35. ^ Pielke, Roger A. (2002). Modelado meteorológico de mesoescala . Academic Press . Págs. 18-19. ISBN. 978-0-12-554766-6.
  36. ^ ab Strikwerda, John C. (2004). Esquemas de diferencias finitas y ecuaciones diferenciales parciales. SIAM. pp. 165–170. ISBN 978-0-89871-567-5.
  37. ^ Pielke, Roger A. (2002). Modelado meteorológico de mesoescala . Academic Press . pág. 65. ISBN. 978-0-12-554766-6.
  38. ^ Pielke, Roger A. (2002). Modelado meteorológico de mesoescala . Academic Press . Págs. 285-287. ISBN. 978-0-12-554766-6.
  39. ^ Sunderam, VS; van Albada, G. Dick; Pedro, MA; Sloot, JJ Dongarra (2005). Ciencias Computacionales - ICCS 2005: Quinta Conferencia Internacional, Atlanta, GA, EE. UU., 22 al 25 de mayo de 2005, Actas, Parte 1. Springer. pag. 132.ISBN​ 978-3-540-26032-5.
  40. ^ Zwieflhofer, Walter; Kreitz, Norbert; Centro Europeo de Previsiones Meteorológicas a Mediano Plazo (2001). Avances en teracomputación: actas del noveno taller del ECMWF sobre el uso de la informática de alto rendimiento en meteorología. World Scientific. pág. 276. ISBN 978-981-02-4761-4.{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
  41. ^ Chan, Johnny CL y Jeffrey D. Kepert (2010). Perspectivas globales sobre los ciclones tropicales: de la ciencia a la mitigación. World Scientific. págs. 295-296. ISBN 978-981-4293-47-1. Consultado el 24 de febrero de 2011 .
  42. ^ Holton, James R. (2004). Introducción a la meteorología dinámica, volumen 1. Academic Press. pág. 480. ISBN 978-0-12-354015-7. Consultado el 24 de febrero de 2011 .
  43. ^ Brown, Molly E. (2008). Sistemas de alerta temprana de hambruna y datos de teledetección. Springer. p. 121. Bibcode :2008fews.book.....B. ISBN 978-3-540-75367-4. Consultado el 24 de febrero de 2011 .
  44. ^ Ahrens, C. Donald (2008). Fundamentos de meteorología: una invitación a la atmósfera. Cengage Learning. pág. 244. ISBN 978-0-495-11558-8.
  45. ^ Narita, Masami y Shiro Ohmori (6 de agosto de 2007). "3.7 Mejora de los pronósticos de precipitación mediante el modelo de mesoescala no hidrostático operacional con la parametrización convectiva de Kain-Fritsch y la microfísica de nubes" (PDF) . 12.ª Conferencia sobre procesos de mesoescala . Consultado el 15 de febrero de 2011 .
  46. ^ Frierson, Dargan (14 de septiembre de 2000). "El esquema de parametrización de nubes diagnósticas" (PDF) . Universidad de Washington . págs. 4-5. Archivado desde el original (PDF) el 1 de abril de 2011 . Consultado el 15 de febrero de 2011 .
  47. ^ Stensrud, David J. (2007). Esquemas de parametrización: claves para entender los modelos numéricos de predicción meteorológica. Cambridge University Press. p. 6. ISBN 978-0-521-86540-1.
  48. ^ McGuffie, K. y A. Henderson-Sellers (2005). Introducción a la modelización climática . John Wiley and Sons. pág. 188. ISBN 978-0-470-85751-9.
  49. ^ Melʹnikova, Irina N. y Alexander V. Vasilyev (2005). Radiación solar de onda corta en la atmósfera terrestre: cálculo, observación, interpretación. Springer. pp. 226–228. ISBN 978-3-540-21452-6.
  50. ^ Stensrud, David J. (2007). Esquemas de parametrización: claves para comprender los modelos numéricos de predicción meteorológica. Cambridge University Press. pp. 12–14. ISBN 978-0-521-86540-1.
  51. ^ Baklanov, Alexander, Sue Grimmond, Alexander Mahura (2009). Modelos meteorológicos y de calidad del aire para áreas urbanas. Springer. Págs. 11-12. ISBN. 978-3-642-00297-7. Consultado el 24 de febrero de 2011 .{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
  52. ^ Warner, Thomas Tomkins (2010). Predicción numérica del clima y el tiempo. Cambridge University Press . pág. 259. ISBN 978-0-521-51389-0.
  53. ^ Lynch, Peter (2006). "Las ecuaciones fundamentales". El surgimiento de la predicción numérica del tiempo . Cambridge University Press . pp. 45–46. ISBN 978-0-521-85729-1.
  54. ^ Ahrens, C. Donald (2008). Fundamentos de meteorología: una invitación a la atmósfera. Cengage Learning. pág. 10. ISBN 978-0-495-11558-8.
  55. ^ Janjic, Zavisa; Gall, Robert; Pyle, Matthew E. (febrero de 2010). "Documentación científica para el solucionador NMM" (PDF) . Centro Nacional de Investigación Atmosférica . págs. 12-13. Archivado desde el original (PDF) el 23 de agosto de 2011 . Consultado el 3 de enero de 2011 .
  56. ^ Pielke, Roger A. (2002). Modelado meteorológico de mesoescala . Academic Press . Págs. 131-132. ISBN. 978-0-12-554766-6.
  57. ^ Baum, Marsha L. (2007). Cuando la naturaleza ataca: desastres climáticos y la ley. Greenwood Publishing Group. pág. 189. ISBN 978-0-275-22129-4.
  58. ^ Glahn, Harry R.; Lowry, Dale A. (diciembre de 1972). "El uso de estadísticas de salida del modelo (MOS) en la predicción meteorológica objetiva". Journal of Applied Meteorology . 11 (8): 1203–1211. Bibcode :1972JApMe..11.1203G. doi : 10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 .
  59. ^ Gultepe, Ismail (2007). Niebla y nubes de capa límite: visibilidad y pronóstico de la niebla. Springer. p. 1144. ISBN 978-3-7643-8418-0. Recuperado el 11 de febrero de 2011 .
  60. ^ Barry, Roger Graham; Chorley, Richard J. (2003). Atmósfera, tiempo y clima. Psychology Press. pág. 172. ISBN 978-0-415-27171-4. Recuperado el 11 de febrero de 2011 .
  61. ^ ab Cox, John D. (2002). Vigilantes de tormentas. John Wiley & Sons, Inc., págs. 222-224. ISBN 978-0-471-38108-2.
  62. ^ ab Manousos, Peter (19 de julio de 2006). "Sistemas de predicción por conjuntos". Centro de predicción hidrometeorológica . Consultado el 31 de diciembre de 2010 .
  63. ^ Weickmann, Klaus; Jeff Whitaker; Andres Roubicek; Catherine Smith (1 de diciembre de 2001). "El uso de pronósticos por conjuntos para producir pronósticos meteorológicos mejorados a mediano plazo (3 a 15 días)". Centro de Diagnóstico Climático . Archivado desde el original el 28 de mayo de 2010. Consultado el 16 de febrero de 2007 .
  64. ^ Chakraborty, Arindam (octubre de 2010). "La habilidad de los pronósticos a medio plazo del ECMWF durante el año de convección tropical de 2008". Monthly Weather Review . 138 (10): 3787–3805. Bibcode :2010MWRv..138.3787C. doi : 10.1175/2010MWR3217.1 .
  65. ^ Epstein, ES (diciembre de 1969). "Predicción dinámica estocástica". Tellus A. 21 (6): 739–759. Bibcode : 1969 Dile...21..739E. doi :10.1111/j.2153-3490.1969.tb00483.x.
  66. ^ Leith, CE (junio de 1974). "Habilidad teórica de los pronósticos de Monte Carlo". Monthly Weather Review . 102 (6): 409–418. Código Bibliográfico :1974MWRv..102..409L. doi : 10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 .
  67. ^ "MOGREPS". Oficina Meteorológica . Archivado desde el original el 22 de octubre de 2012. Consultado el 1 de noviembre de 2012 .
  68. ^ ab Warner, Thomas Tomkins (2010). Predicción numérica del clima y el tiempo. Cambridge University Press . págs. 266-275. ISBN 978-0-521-51389-0.
  69. ^ Palmer, TN ; Shutts, GJ; Hagedorn, R.; Doblas-Reyes, FJ; Jung, T.; Leutbecher, M. (mayo de 2005). "Representación de la incertidumbre del modelo en la predicción meteorológica y climática". Revisión anual de ciencias de la Tierra y planetarias . 33 : 163–193. Código Bibliográfico :2005AREPS..33..163P. doi :10.1146/annurev.earth.33.092203.122552.
  70. ^ Grimit, Eric P.; Mass, Clifford F. (octubre de 2004). "Redefiniendo la relación de habilidad y propagación de conjuntos desde una perspectiva probabilística" (PDF) . Universidad de Washington . Archivado desde el original (PDF) el 2008-10-12 . Consultado el 2010-01-02 .
  71. ^ Zhou, Binbin; Du, Jun (febrero de 2010). "Predicción de niebla a partir de un sistema de predicción de conjunto de mesoescala multimodelo" (PDF) . Weather and Forecasting . 25 (1): 303. Bibcode :2010WtFor..25..303Z. doi :10.1175/2009WAF2222289.1. S2CID  4947206 . Consultado el 2 de enero de 2011 .
  72. ^ Cane, D.; Milelli, M. (12 de febrero de 2010). "Técnica de SuperEnsemble multimodelo para pronósticos cuantitativos de precipitación en la región de Piemonte" (PDF) . Natural Hazards and Earth System Sciences . 10 (2): 265. Bibcode :2010NHESS..10..265C. doi : 10.5194/nhess-10-265-2010 . Consultado el 2 de enero de 2011 .
  73. ^ Daly, Aaron y Paolo Zannetti (2007). Contaminación del aire ambiental (PDF) . The Arab School for Science and Technology y The EnviroComp Institute. pág. 16. Consultado el 24 de febrero de 2011 .
  74. ^ ab Baklanov, Alexander; Rasmussen, Alix; Fay, Barbara; Berge, Erik; Finardi, Sandro (septiembre de 2002). "Potencial y deficiencias de los modelos numéricos de predicción meteorológica en la provisión de datos meteorológicos para la previsión de la contaminación atmosférica urbana". Contaminación del agua, el aire y el suelo: foco de atención . 2 (5): 43–60. doi :10.1023/A:1021394126149. S2CID  94747027.
  75. ^ Marshall, John; Plumb, R. Alan (2008). Atmósfera, océano y dinámica climática: un texto introductorio . Ámsterdam: Elsevier Academic Press. pp. 44–46. ISBN 978-0-12-558691-7.
  76. ^ Oficina Australiana de Estadísticas (2005). Anuario, Australia, número 87. pág. 40. Consultado el 18 de febrero de 2011 .
  77. ^ Celebración del 200.° aniversario de la Administración Nacional Oceánica y Atmosférica (22 de mayo de 2008). «El primer modelo climático». Administración Nacional Oceánica y Atmosférica . Consultado el 20 de abril de 2010 .{{cite web}}: CS1 maint: nombres numéricos: lista de autores ( enlace )
  78. ^ Bridgman, Howard A., John E. Oliver, Michael H. Glantz (2006). El sistema climático global: patrones, procesos y teleconexiones. Cambridge University Press. pp. 284–289. ISBN 978-0-521-82642-6. Recuperado el 18 de febrero de 2011 .{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )
  79. ^ Chalikov, DV (agosto de 1978). "La simulación numérica de la interacción viento-ola". Journal of Fluid Mechanics . 87 (3): 561–82. Bibcode :1978JFM....87..561C. doi :10.1017/S0022112078001767. S2CID  122742282.
  80. ^ Lin, Pengzhi (2008). Modelado numérico de ondas de agua. Psychology Press. pág. 270. ISBN 978-0-415-41578-1.
  81. ^ Bender, Leslie C. (enero de 1996). "Modificación de la física y la numérica en un modelo de olas oceánicas de tercera generación". Journal of Atmospheric and Oceanic Technology . 13 (3): 726–750. Bibcode :1996JAtOT..13..726B. doi : 10.1175/1520-0426(1996)013<0726:MOTPAN>2.0.CO;2 .
  82. ^ Centro Nacional de Huracanes (julio de 2009). «Resumen técnico de los modelos de trayectoria e intensidad del Centro Nacional de Huracanes» (PDF) . Administración Nacional Oceánica y Atmosférica . Consultado el 19 de febrero de 2011 .
  83. ^ Franklin, James (20 de abril de 2010). "Verificación de pronóstico del Centro Nacional de Huracanes". Centro Nacional de Huracanes . Consultado el 2 de enero de 2011 .
  84. ^ Rappaport, Edward N.; Franklin, James L.; Avila, Lixion A.; Baig, Stephen R.; Beven II, John L.; Blake, Eric S.; Burr, Christopher A.; Jiing, Jiann-Gwo; Juckins, Christopher A.; Knabb, Richard D.; Landsea, Christopher W.; Mainelli, Michelle; Mayfield, Max; McAdie, Colin J.; Pasch, Richard J.; Sisko, Christopher; Stewart, Stacy R.; Tribble, Ahsha N. (abril de 2009). "Avances y desafíos en el Centro Nacional de Huracanes". Tiempo y pronóstico . 24 (2): 395–419. Código Bibliográfico :2009WtFor..24..395R. CiteSeerX 10.1.1.207.4667 . doi :10.1175/2008WAF2222128.1.S2CID 14845745  . 
  85. ^ ab Sullivan, Andrew L. (junio de 2009). "Modelado de la propagación de incendios en la superficie de áreas forestales, 1990-2007. 1: modelos físicos y cuasifísicos". Revista Internacional de Incendios Forestales . 18 (4): 349. arXiv : 0706.3074 . doi :10.1071/WF06143. S2CID  16173400.
  86. ^ Asensio, MI y L. Ferragut (2002). "Sobre un modelo de incendios forestales con radiación". Revista Internacional de Métodos Numéricos en Ingeniería . 54 (1): 137–157. Bibcode :2002IJNME..54..137A. doi :10.1002/nme.420. S2CID  122302719.
  87. ^ Mandel, Jan, Lynn S. Bennethum , Jonathan D. Beezley, Janice L. Coen , Craig C. Douglas, Minjeong Kim y Anthony Vodacek (2008). "Un modelo de incendios forestales con asimilación de datos". Matemáticas y computadoras en simulación . 79 (3): 584–606. arXiv : 0709.0086 . Bibcode :2007arXiv0709.0086M. doi :10.1016/j.matcom.2008.03.015. S2CID  839881.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
  88. ^ Clark, TL, MA Jenkins, J. Coen y David Packham (1996). "Un modelo acoplado de atmósfera e incendios: número de Froude convectivo y digitación dinámica". Revista internacional de incendios forestales . 6 (4): 177–190. doi :10.1071/WF9960177.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
  89. ^ Clark, Terry L., Marry Ann Jenkins, Janice Coen y David Packham (1996). "Un modelo acoplado atmósfera-incendio: retroalimentación convectiva en la dinámica de la línea de fuego". Journal of Applied Meteorology . 35 (6): 875–901. Bibcode :1996JApMe..35..875C. doi : 10.1175/1520-0450(1996)035<0875:ACAMCF>2.0.CO;2 .{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
  90. ^ Rothermel, Richard C. (enero de 1972). "Un modelo matemático para predecir la propagación del fuego en incendios forestales" (PDF) . Servicio Forestal de los Estados Unidos . Consultado el 28 de febrero de 2011 .

Lectura adicional

Enlaces externos