stringtranslate.com

Macla de cristales

Cuarzo – gemelo japonés
Diagrama de cristales maclados de albita . En la exfoliación más perfecta, que es paralela al plano basal (P), hay un sistema de estrías finas, paralelas a la segunda exfoliación (M).

La macla de cristales se produce cuando dos o más cristales adyacentes del mismo mineral se orientan de forma que comparten algunos de los mismos puntos de la red cristalina de manera simétrica. El resultado es un crecimiento conjunto de dos cristales separados que están fuertemente unidos entre sí. La superficie a lo largo de la cual se comparten los puntos de la red en los cristales maclados se denomina superficie de composición o plano maclado.

Los cristalógrafos clasifican los cristales maclados según una serie de leyes de maclado, que son específicas de la estructura cristalina. El tipo de maclado puede ser una herramienta de diagnóstico en la identificación de minerales. Hay tres tipos principales de maclado. El primero es el maclado de crecimiento, que puede ocurrir tanto en partículas muy grandes como en partículas muy pequeñas. El segundo es el maclado de transformación, en el que hay un cambio en la estructura cristalina. El tercero es el maclado de deformación, en el que el maclado se desarrolla en un cristal en respuesta a una tensión de corte , y es un mecanismo importante para los cambios de forma permanentes en un cristal.

Definición

Red gemela (2D). La línea roja horizontal larga es el plano de composición donde se unen los dos segmentos cristalinos. La red cristalina superior es el reflejo de la red cristalina inferior. Los puntos rojos son los puntos compartidos de la red cristalina.

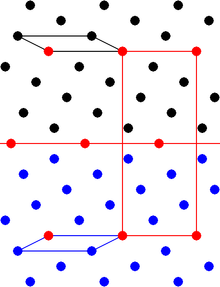
El maclado es una forma de intercrecimiento simétrico entre dos o más cristales adyacentes del mismo mineral. Se diferencia del intercrecimiento aleatorio ordinario de granos minerales en un depósito mineral, porque las orientaciones relativas de los dos segmentos de cristal muestran una relación fija que es característica de la estructura mineral. La relación se define mediante una operación de simetría llamada operación de maclado . [1] [2]

La operación de macla no es una de las operaciones de simetría normales de la estructura cristalina no maclada. Por ejemplo, la operación de macla puede ser una reflexión a través de un plano que no es un plano de simetría del monocristal. [1] [2]

A nivel microscópico, el límite maclado se caracteriza por un conjunto de posiciones atómicas en la red cristalina que se comparten entre las dos orientaciones. [1] [2] Estos puntos reticulares compartidos le dan a la unión entre los segmentos cristalinos una resistencia mucho mayor que la que existe entre granos orientados aleatoriamente, de modo que los cristales maclados no se separan fácilmente. [3]

El crecimiento paralelo describe una forma de crecimiento de cristales que produce la apariencia de un grupo de cristales alineados que podrían confundirse con maclas. Un examen minucioso revela que el grupo es en realidad un solo cristal. No se trata de macla, ya que la red cristalina es continua en todo el grupo. El crecimiento paralelo probablemente se produce porque reduce la energía del sistema. [4]

Leyes gemelas

Las leyes de macla son operaciones de simetría que definen la orientación entre segmentos de cristales gemelos. Estas son tan características del mineral como los ángulos de sus caras cristalinas. Por ejemplo, los cristales de estaurolita muestran macla en ángulos de casi exactamente 90 grados o 30 grados. [3] Una ley de macla no es una operación de simetría del conjunto completo de puntos base. [2]

Las leyes de macla incluyen operaciones de reflexión, operaciones de rotación y la operación de inversión. La macla de reflexión se describe mediante los índices de Miller del plano de macla (es decir, {hkl}), mientras que la macla rotacional se describe mediante la dirección del eje de macla (es decir, <hkl>). La macla de inversión es típicamente equivalente a una simetría de reflexión o rotación. [1]

Las leyes de macla rotacional son casi siempre rotaciones de doble rotación, aunque es posible cualquier otra simetría de rotación permitida (triple, cuádruple, quíntuple o séxtuple). El eje de macla será perpendicular a un plano reticular. [5] Es posible que una ley de macla rotacional comparta el mismo eje que una simetría rotacional del cristal individual si la ley de macla es una rotación de doble rotación y la operación de simetría es una rotación de triple rotación. Este es el caso de la macla por ley de espinela en <111>: la estructura de espinela tiene una simetría rotacional de triple rotación en <111> y la espinela suele estar maclada por rotación de doble rotación en <111>. [1]

El límite entre los segmentos del cristal se denomina superficie de composición o, si es plana, plano de composición . El plano de composición es a menudo, aunque no siempre, paralelo al plano de ley de macla de una ley de reflexión. Si este es el caso, el plano de macla siempre es paralelo a una posible cara del cristal. [2]

Leyes comunes sobre gemelos

Macla de contacto según la ley de la espinela. A la izquierda se muestra un monocristal con el plano de composición en rojo. A la derecha, el cristal se ha cortado en el plano de composición y la mitad delantera se ha rotado 180° para producir una macla de contacto. Esto crea reentrantes en la parte superior, inferior izquierda e inferior derecha del plano de composición. [3]

En el sistema isométrico, los tipos de maclas más comunes son la Ley de Espinela (plano maclado, paralelo a un octaedro ) <111>, donde el eje maclado es perpendicular a una cara octaédrica, y la Cruz de Hierro <001>, que es la interpenetración de dos piritoedros, un subtipo de dodecaedro . [6]

En el sistema hexagonal, la calcita muestra las leyes de macla de contacto {0001} y {0112}. El cuarzo muestra la ley de Brasil {1120} y la ley de Dauphiné <0001>, que son maclas de penetración causadas por transformación, y la ley de Japón {1122}, que a menudo es causada por accidentes durante el crecimiento. [6]

En el sistema tetragonal, las maclas de contacto cíclicas son el tipo de macla observado más comúnmente, como en el dióxido de titanio rutilo y el óxido de estaño casiterita . [6]

En el sistema ortorrómbico, los cristales generalmente se maclan en planos paralelos a la cara del prisma, donde la más común es una macla {110}, que produce maclas cíclicas, como en aragonito , crisoberilo y cerusita . [6]

En el sistema monoclínico, las maclas ocurren con mayor frecuencia en los planos {100} y {001} según la Ley de Manebach {001}, la Ley de Carlsbad [001], la Ley de Baveno {021} en ortoclasa y las maclas de cola de golondrina (ley de Manebach) {001} en yeso . [6]

En el sistema triclínico, los cristales maclados más comunes son los minerales feldespáticos plagioclasa y microclina . Estos minerales muestran las leyes de la albita y la periclina. [5] [6]

A continuación se enumeran las operaciones de maclado más comunes por sistema cristalino . Esta lista no es exhaustiva, en particular para los sistemas cristalinos de menor simetría, como el sistema triclínico. [7] [1] [6]

Macla de estaurolita de 30°
Maclas de 90° de estaurolita
Macla cruzada de pirita de hierro

Tipos de hermanamiento

Crisoberilo que muestra macla cíclica

Los cristales maclados simples pueden ser maclados por contacto o maclados por penetración. Los maclados por contacto se encuentran en un único plano de composición, a menudo apareciendo como imágenes especulares a través del límite. La plagioclasa , el cuarzo , el yeso y la espinela a menudo exhiben maclado por contacto. [3] El maclado meroédrico ocurre cuando las redes de los maclados por contacto se superponen en tres dimensiones, como por la rotación relativa de un maclado con respecto al otro. [8] Un ejemplo es la metazeunerita . [9] El maclado por contacto crea característicamente caras reentrantes donde las caras de los segmentos de cristal se encuentran en el plano de contacto en un ángulo mayor a 180°. [3]

Un tipo de maclado que implica relaciones de 180° se llama hemitropismo o hemitropía .

En las maclas de penetración, los cristales individuales tienen la apariencia de atravesarse entre sí de manera simétrica. [3] La ortoclasa , la estaurolita , la pirita y la fluorita a menudo muestran maclas de penetración. La superficie de composición en las maclas de penetración suele ser irregular y se extiende hasta el centro del cristal. [2]

El maclado por contacto puede surgir por reflexión o rotación, mientras que el maclado por penetración generalmente se produce por rotación. [2]

Si varias partes de un cristal maclado están alineadas según la misma ley de macla, se las denomina maclas múltiples o repetidas . Si estas maclas múltiples están alineadas en paralelo, se las denomina maclas polisintéticas . Cuando las maclas múltiples no son paralelas, se las denomina maclas cíclicas . La albita , la calcita y la pirita suelen mostrar macla polisintética. La macla polisintética poco espaciada suele observarse como estrías o líneas finas paralelas en la cara del cristal.Las maclas cíclicas son causadas por maclas repetidas alrededor de un eje de rotación. Este tipo de macla ocurre alrededor de ejes de tres, cuatro, cinco, seis u ocho pliegues; los patrones correspondientes se denominan maclas triples, cuádruples, quíntuples , séxtuples y óctuples. Las maclas séxtuples son comunes en la aragonita. [10] [11] El rutilo , la aragonita , la cerusita y el crisoberilo a menudo presentan maclas cíclicas, típicamente en un patrón radial. [3] [2]

En el caso del maclado rotacional, la relación entre el eje gemelo y el plano gemelo se divide en tres tipos: [12]

  1. maclado paralelo, cuando el eje gemelo y el plano compositivo se encuentran paralelos entre sí,
  2. maclado normal, cuando el plano de macla y el plano de composición se encuentran normalmente, y
  3. maclado complejo, una combinación de maclado paralelo y maclado normal en un plano compositivo.

Modos de formación

Crecimiento paralelo de piromorfita

Hay tres modos de formación de cristales maclados.

Hermanamiento de crecimiento (nanotwinning)

Quíntuple gemelo en una nanopartícula de oro ( micrografía de microscopio electrónico ).

Hay dos tipos de maclado que pueden ocurrir durante el crecimiento: accidental y aquel en el que la estructura maclada tiene menor energía.

En el maclado por crecimiento accidental, un átomo se une a una cara de cristal en una posición poco ideal, formando una semilla para el crecimiento de un maclado. El cristal original y su maclado crecen juntos y se parecen mucho entre sí. Esto es lo suficientemente característico de ciertos minerales como para sugerir que se ve favorecido termodinámica o cinéticamente en condiciones de crecimiento rápido. [3] [1]

A diferencia de estos, se encuentran maclas en nanopartículas como la imagen aquí, siendo estas nanopartículas quíntuples o decaédricas una de las más comunes. [14] Estas maclas cíclicas ocurren ya que son más bajas en energía en tamaños pequeños. [15] Para el caso quíntuple mostrado, hay una disclinación a lo largo del eje común [16] que conduce a una energía de deformación adicional. [17] Para equilibrar esto, hay una reducción en la energía libre superficial, en gran parte debido a más (111) facetas superficiales. [18] En nanopartículas pequeñas, la estructura decaédrica y una estructura icosaédrica más complicada (con veinte unidades) son de menor energía, pero a energías mayores los monocristales se vuelven de menor energía. [19] [20] Sin embargo, no tienen que transformarse en monocristales y pueden crecer mucho, y se conocen como quíntuples, documentados ya en 1831 por Gustav Rose ; [21] Hay más dibujos disponibles en el Atlas der Kristallformen, y véase también el artículo sobre los quintillos . [22]

Hermanamiento de transformación

Ilustración de maclado por transformación en 2D. El cristal ortorrómbico de la izquierda se transforma en un cristal monoclínico de la derecha, con dos planos de maclado paralelos (maclado polisintético)

El maclado por transformación y recocido se produce cuando un cristal que se enfría experimenta una transición polimórfica desplazativa. Por ejemplo, la leucita tiene una estructura cristalina isométrica por encima de aproximadamente 665 °C (1229 °F), pero se vuelve tetragonal por debajo de esta temperatura. Cualquiera de los tres ejes originales de un cristal puede convertirse en el eje largo cuando se produce este cambio de fase. El maclado se produce cuando diferentes partes del cristal rompen su simetría isométrica a lo largo de una elección diferente de eje. Esto es típicamente maclado polisintético, que permite que el cristal mantenga su forma isométrica promediando el desplazamiento en cada dirección. Esto produce un cristal pseudomórfico que parece tener simetría isométrica. El feldespato potásico también experimenta maclado polisintético a medida que se transforma de una estructura monoclínica ( ortoclasa ) a una estructura triclínica ( microclina ) al enfriarse lentamente. [1]

Maclado por deformación

Animación del maclado por deformación de cristales.

El maclado por deformación es una respuesta a la tensión de corte. La estructura cristalina se desplaza a lo largo de planos sucesivos del cristal, un proceso también llamado maclado por deslizamiento . El maclado es siempre maclado por reflexión y el plano de deslizamiento es también el plano especular. El maclado por deformación se puede observar en un fragmento de clivaje de calcita aplicando una presión suave con la hoja de un cuchillo cerca de un borde. Este maclado por deslizamiento en particular, {102}, se encuentra casi universalmente en lechos de rocas deformadas que contienen calcita. [1]

El maclado y el deslizamiento son mecanismos competitivos para la deformación de los cristales. Cada mecanismo es dominante en ciertos sistemas cristalinos y bajo ciertas condiciones. [23] En los metales fcc , el deslizamiento es casi siempre dominante porque la tensión requerida es mucho menor que la tensión de maclado. [24]

El maclado puede producirse por desplazamiento cooperativo de átomos a lo largo de la superficie del límite de maclado. Este desplazamiento simultáneo de una gran cantidad de átomos requiere una energía significativa para realizarse. Por lo tanto, la tensión teórica necesaria para formar un maclado es bastante alta. Se cree que el maclado está asociado con el movimiento de dislocación en una escala coordinada, en contraste con el deslizamiento, que es causado por un deslizamiento independiente en varias ubicaciones en el cristal .

En comparación con el deslizamiento, el maclado produce un patrón de deformación que es más heterogéneo por naturaleza. Esta deformación produce un gradiente local a lo largo del material y cerca de las intersecciones entre maclados y límites de grano. El gradiente de deformación puede provocar fracturas a lo largo de los límites, en particular en metales de transición bcc a bajas temperaturas.

De las tres estructuras cristalinas comunes bcc , fcc y hcp , la estructura hcp es la que tiene más probabilidades de formar maclas de deformación cuando se somete a deformación, porque rara vez tienen una cantidad suficiente de sistemas de deslizamiento para un cambio de forma arbitrario. Las altas tasas de deformación, la baja energía de falla de apilamiento y las bajas temperaturas facilitan la macla de deformación. [25]

Si un metal con estructura cúbica centrada en las caras (fcc), como Al, Cu, Ag, Au, etc., se somete a tensión, experimentará maclado. La formación y migración de los límites de maclado es en parte responsable de la ductilidad y maleabilidad de los metales fcc. [26]

Los límites de macla son en parte responsables del endurecimiento por choque y de muchos de los cambios que ocurren en el trabajo en frío de metales con sistemas de deslizamiento limitado o a temperaturas muy bajas. También ocurren debido a transformaciones martensíticas : el movimiento de los límites de macla es responsable del comportamiento pseudoelástico y de memoria de forma del nitinol , y su presencia es en parte responsable de la dureza debido al temple del acero . En ciertos tipos de aceros de alta resistencia, las maclas de deformación muy finas actúan como obstáculos primarios contra el movimiento de dislocación. Estos aceros se conocen como aceros 'TWIP', donde TWIP significa plasticidad inducida por maclaje . [27]

Cristalografía por maclado de deformación

Planos cristalográficos de maclado por deformación

La macla se define cristalográficamente por su plano de macla 𝑲 𝟏 , el plano de simetría en la macla y el material original, y 𝜼 𝟏, que es la dirección de cizallamiento de macla. Las maclas de deformación en Zr tienen generalmente forma lenticular, alargándose en la dirección 𝜼 𝟏 y engrosándose a lo largo de la normal al plano 𝑲 𝟏 . [28]

El plano gemelo, la dirección de corte y el plano de corte forman los vectores base de un conjunto ortogonal. La relación de desorientación del eje-ángulo entre el padre y el gemelo es una rotación del ángulo 𝜉 sobre la dirección normal 𝑷 del plano de corte.

De manera más general, la gemelación se puede describir como una rotación de 180° sobre un eje ( dirección normal 𝑲 𝟏 para gemelos tipo I o 𝜼 𝟏 para gemelos tipo II), o una reflexión especular en un plano (plano normal 𝑲 𝟏 o 𝜼 𝟏 ). [29]

Además de una cizalladura homogénea, a veces se requieren cambios atómicos para reformar la estructura cristalina correcta en la red maclada. Para cada variante maclada, es posible un maclado recíproco con 𝑲 𝟏 y 𝑲 2 , 𝜼 𝟏 y 𝜼 2 intercambiados , pero una variante puede aparecer con más frecuencia en la realidad debido a las complejidades de los cambios requeridos. [30]

En una acción de cizallamiento solo hay dos planos cristalográficos que no cambian su forma y tamaño como consecuencia del cizallamiento. El primero 𝑲 𝟏 es el plano que define las superficies superior e inferior del volumen cizallado. Este plano contiene la dirección de cizallamiento. El otro plano, designado C. La dirección de cizallamiento se muestra con una flecha y se etiqueta con su designación habitual 𝜼 𝟏 . De lo anterior se desprende que hay tres formas en las que se puede cizallar una red cristalina manteniendo su estructura y simetría cristalinas:

  1. Cuando 𝑲 𝟏 es un plano racional y 𝜼 2 una dirección racional, un gemelo del primer tipo
  2. Cuando 𝑲 2 es un plano racional y 𝜼 𝟏 una dirección racional, un gemelo de segunda especie, raro
  3. Cuando los cuatro elementos 𝑲 𝟏 , 𝑲 2 , 𝜼 𝟏 y 𝜼 2 son racionales, se obtiene un compuesto gemelo

Configuración de maclado por deformación

Planos de maclado regulares en cristales de calcita. Imagen de nicoles cruzados, aumento 10x (campo de visión = 2 mm)

Un embrión de macla de deformación se forma en el metal BCC mediante la acumulación de fallas de apilamiento, con una selección de variantes gobernada por el estado de tensión local. [31] [32] [33] La variación del campo de tensión cerca de las maclas inferida a partir de datos experimentales de HR- EBSD [34] [35] y de simulación de elementos finitos de plasticidad cristalina (CPFE) indicó que las maclas se nuclean en sitios con máxima densidad de energía de deformación y tensión de corte resuelta en las maclas ; por lo tanto, se reduce la energía elástica total después de la formación. Esta relajación depende del espesor de la macla y es un factor decisivo en el espaciamiento entre maclas. [36] El análisis experimental [37] y tridimensional [38] se ha centrado en la densidad de energía de deformación (almacenada) medida a lo largo de una trayectoria. Este campo de tensión altamente localizado puede proporcionar una fuerza impulsora suficiente para la nucleación de maclas simultánea [39] y la nucleación de grietas inter/intragranulares .

El crecimiento de maclas de deformación puede percibirse como un proceso de dos pasos de i) engrosamiento que está mediado por la interacción entre los parciales maclas residuales y móviles en la interfaz macla coherente-madre, [40] y ii) movilidad de dislocación a lo largo de la dirección de corte macla. [41] La macla se propaga cuando la tensión de corte homogénea alcanza un valor crítico, y una interfaz macla-madre avanza dentro del grano madre [240]. La macla de deformación que se propaga genera un campo de tensión debido a su confinamiento por el cristal madre circundante, y las maclas de deformación desarrollan una forma de esferoide oblato 3D (que aparece en secciones 2D como una lente biconvexa ) con una interfaz coherente y no coherente mixta (Figura b). [41]

Kannan et al. [42] descubrieron, utilizando imágenes ópticas de ultraalta velocidad in situ, que la nucleación gemela en magnesio monocristalino está impulsada por la tensión acompañada de una propagación instantánea a una velocidad de 1 km/s (inicialmente) que prioriza el engrosamiento lateral del volumen sobre la propagación hacia adelante, más allá de un ancho crítico donde el crecimiento se vuelve más rápido a lo largo de la dirección de corte. Barnett [43] también indicó que el crecimiento se debe a la extensión de la punta gemela. Además, las simulaciones elásticas del campo de tensión local que rodea la punta gemela elipsoidal encuentran que el campo se puede describir utilizando su ángulo de lente ( ) y que la magnitud del campo de tensión aumenta con el espesor de la punta gemela. [44]

(a) Imagen de diodo electrónico de dispersión anticipada (FSD) para maclas de deformación en el límite de grano en ferrita endurecida por envejecimiento a I) 18 mm de distancia de trabajo y II) 38 mm de distancia de trabajo. (b) Esquema de una macla lenticular con dislocaciones de interfaz y (c) Banda de macla. [45]

En la práctica, la acomodación plástica ocurre en el cristal original ; por lo tanto, también depende de la tensión de fluencia del material, la rigidez elástica anisotrópica de la red cristalina original y la magnitud de la cizalladura por maclado de deformación. [40] Esto también puede ir acompañado de difusión de elementos de largo alcance y segregación elemental (por ejemplo, Cr y Co en la superaleación MD2 basada en Ni de un solo cristal ), que ocurre en el límite maclado para facilitar el crecimiento maclado al reducir la energía crítica de falla de apilamiento. [46] Se ha observado una variación lineal entre el espesor maclado, la energía de falla de apilamiento y el tamaño de grano, [47] y, en menor grado, el estado de tensión del grano maclado ( factor Schmid ). [48] El espesor maclado se saturó una vez que una densidad crítica de dislocaciones residuales alcanzó el límite coherente entre el cristal original y el maclado. [33] [49]

Se ha prestado mucha atención a la cristalografía , [50] morfología [51] y efectos macromecánicos [52] del maclado por deformación. Aunque el criterio para el crecimiento del maclado por deformación no se entiende completamente, es un fenómeno controlado por la punta vinculado a la interacción entre los parciales maclados residuales y móviles en la interfaz maclada; termodinámicamente, esto involucra la energía elástica de la red deformada, la interfaz y la energía libre de volumen del maclado, y la energía disipada del mecanismo de crecimiento. [53] Para entender completamente las interacciones entre la microestructura (es decir, tamaño de grano, textura), temperatura y velocidad de deformación en el maclado por deformación, es crucial caracterizar el (alto) campo local de tensión y deformación asociado con el engrosamiento y propagación del maclado. Esto es especialmente importante para materiales donde la fractura por clivaje puede ser iniciada por maclado (por ejemplo, hierro-silicio, la fase ferrítica del acero inoxidable dúplex endurecido por envejecimiento y magnesio monocristalino ) como un mecanismo de alivio de tensión.

Los primeros estudios de maclas de deformación detenidas dentro de granos de niobio [54] y hierro [55] visualizaron la concentración de deformación altamente local en la punta de la macla utilizando un procedimiento de grabado por picadura. Más recientemente, se ha utilizado la difracción de retrodispersión de electrones de alta resolución (HR- EBSD ) para investigar la "singularidad" de la deformación delante de una punta de la macla en una aleación de circonio de empaquetamiento compacto hexagonal (HCP) . Una macla de deformación en titanio de pureza comercial se caracterizó de manera similar y luego se cuantificó utilizando un factor Schmid local (LSF) en la punta de la macla, [56] como se describe en la ecuación siguiente.

donde σ  es el tensor de tensión, S i es el tensor de Schmid, P i es su parte simétrica, d i es la dirección de corte y n i  es el plano de corte normal para el i -ésimo sistema de deslizamiento . Los autores concluyeron que las condiciones en la punta gemela controlan el engrosamiento y la propagación de una manera análoga a la operación de las fuentes de dislocación delante de la punta de una grieta. [57] En el análisis, una amplia región de LSF alta delante de la punta gemela favoreció la propagación, mientras que una región estrecha de LSF alta promovió el engrosamiento. Desde entonces, se ha argumentado [58] que el LSF controla firmemente la selección de variantes gemelas, ya que el maclado tiene una fuerte polaridad.

La novedad de LSF, en comparación con otros criterios para describir las condiciones en la macla [47] , radica en combinar un criterio geométrico con el campo de deformación en el grano original para proporcionar una indicación aproximada del modo macla local (es decir, engrosamiento o propagación). Sin embargo, el análisis LSF no aprovecha los datos de campo completo disponibles, se basa en información global sobre la tensión aplicada y no considera el balance de energía que impulsa el crecimiento macla. Ha habido pocos experimentos in situ para cuantificar el campo de deformación antes de una macla de deformación que se propaga. [45] [35] Tales observaciones podrían validar criterios geométricos o híbridos geométricos-energéticos [58] para el crecimiento. Las pruebas a nanoescala (es decir, microscopía electrónica de transmisión ) pueden no representar el comportamiento en muestras a granel debido a la falta de plasticidad, es decir, una gran relación entre el área de superficie y el volumen, [59] por lo que se necesita un método de análisis adecuado.

Lloyd [49] describió el campo de concentración de tensión delante de la punta gemela utilizando un modelo bidimensional basado en dislocaciones dentro de un solo grano de magnesio . Wang y Li, [60] que consideraron modelos microscópicos de campo de fase (MPF) de grietas, notaron que los campos de tensión eran similares para dislocaciones , maclado por deformación y transformaciones martensíticas , con diferencias solo en la tracción de la superficie creada, es decir, hay una recuperación de tracción del 100% para dislocaciones y una superficie libre de tracción para una grieta. Destacaron que la singularidad del campo de tensión regula el avance de la punta de la grieta y las dislocaciones . Esta concentración de tensión se puede caracterizar utilizando una integral de línea independiente de la trayectoria , como lo muestran Eshelby para dislocaciones considerando la contribución de la tracción superficial y las inclusiones elipsoidales , [61] y Rice [62] para grietas y concentraciones de tensión con superficies libres de tracción. Además, Venables [63] señaló que la forma esferoide achatada de la punta gemela es el ejemplo ideal de una inclusión elipsoide o una muesca.

Véase también

Wikimedia Commons tiene medios relacionados con Cristales maclados .

Referencias

  1. ^ abcdefghi Nesse, William D. (2000). Introducción a la mineralogía . Nueva York: Oxford University Press. pp. 87–91. ISBN 9780195106916.
  2. ^ abcdefgh Klein, Cornelis; Hurlbut, Cornelius S. Jr. (1993). Manual de mineralogía: (según James D. Dana) (21.ª ed.). Nueva York: Wiley. págs. 102–106. ISBN 047157452X.
  3. ^ abcdefgh Sinkankas, John (1964). Mineralogía para aficionados . Princeton, NJ: Van Nostrand. pp. 96–105. ISBN 0442276249.
  4. ^ Klein y Hurlbut 1993, pág. 101.
  5. ^ ab Nelson, Stephen A. (2013). "Twinning, Polymorphism, Polytipism, Pseudomorphism". Universidad de Tulane . Consultado el 19 de febrero de 2022 .
  6. ^ abcdefg Klein y Hurlbut 1993, págs. 104-106.
  7. ^ Nesse 2000, págs. 89, 214-216.
  8. ^ Yeates, Todd O. (1997). "[22] Detección y superación de la macla cristalina". Cristalografía macromolecular, parte A. Métodos en enzimología. Vol. 276. págs. 344–358. doi :10.1016/S0076-6879(97)76068-3. ISBN 9780121821777. Número de identificación personal  27799105.
  9. ^ Locock, AJ; Burns, PC (1 de abril de 2003). "Estructuras cristalinas y síntesis de los miembros con predominio de cobre de los grupos autunita y metaautunita: torbernita, zeunerita, metatorbernita y metazeunerita". The Canadian Mineralogist . 41 (2): 489–502. Código Bibliográfico :2003CaMin..41..489L. doi :10.2113/gscanmin.41.2.489.
  10. ^ Dyar y Gunter 2008, págs. 41–43
  11. ^ Chesterman y Lowe 2008, pág. 39
  12. ^ Tobi, Alexander C. (1961). «El reconocimiento de maclas de plagioclasa en secciones normales al plano de composición». American Mineralogist . 46 (11–12): 1470–1488 . Consultado el 19 de febrero de 2022 .
  13. ^ Klein y Hurlbut 1993, pág. 167.
  14. ^ Hofmeister, H. (1998). <3::aid-crat3>3.0.co;2-3 "Estudio de cuarenta años de estructuras macladas quíntuples en partículas pequeñas y películas delgadas". Investigación y tecnología de cristales . 33 (1): 3–25. Bibcode :1998CryRT..33....3H. doi :10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3. ISSN  0232-1300.
  15. ^ Marks, Laurence. D. (2023), "Forma, termodinámica y cinética de nanopartículas", Enciclopedia de nanomateriales , Elsevier, págs. 383–417, doi :10.1016/b978-0-12-822425-0.00082-8, ISBN 978-0-12-822423-6, consultado el 11 de julio de 2023
  16. ^ Wit, R de (1972). "Disclinaciones parciales". Journal of Physics C: Solid State Physics . 5 (5): 529–534. Bibcode :1972JPhC....5..529D. doi :10.1088/0022-3719/5/5/004. ISSN  0022-3719.
  17. ^ Howie, A.; Marks, LD (1984). "Deformaciones elásticas y balance de energía para partículas macladas múltiples". Philosophical Magazine A . 49 (1): 95–109. Bibcode :1984PMagA..49...95H. doi :10.1080/01418618408233432. ISSN  0141-8610.
  18. ^ Marks, LD (1984). "Estructura superficial y energética de partículas macladas múltiples". Philosophical Magazine A . 49 (1): 81–93. Bibcode :1984PMagA..49...81M. doi :10.1080/01418618408233431. ISSN  0141-8610.
  19. ^ Baletto, Francesca; Ferrando, Riccardo (2005). "Propiedades estructurales de los nanocúmulos: efectos energéticos, termodinámicos y cinéticos". Reseñas de Física Moderna . 77 (1): 371–423. Bibcode :2005RvMP...77..371B. doi :10.1103/RevModPhys.77.371. ISSN  0034-6861.
  20. ^ Rogers, Blake; Lehr, Alexander; Velázquez-Salazar, J. Jesús; Whetten, Robert; Mendoza-Cruz, Ruben; Bazan-Diaz, Lourdes; Bahena-Uribe, Daniel; José Yacaman, Miguel (2023). "Decahedra e icosaedra por todas partes: la cristalización anómala de Au y otros metales a escala nanométrica". Investigación y tecnología de cristales . 58 (4). Código Bibliográfico :2023CryRT..5800259R. doi :10.1002/crat.202200259. ISSN  0232-1300.
  21. ^ Rosa, Gustav (1831). "Ueber die Krystallformen des Goldes und des Silbers". Annalen der Physik . 99 (10): 196-204. Código bibliográfico : 1831AnP....99..196R. doi : 10.1002/andp.18310991003. ISSN  0003-3804.
  22. ^ Goldschmidt, V (1918). Atlas der Kristallformen, V4, Láminas. Carl Winters Universitätsbuchhandlung. págs. Tafel 48, Fig. 21. (Oro). hdl :2027/nyp.33433084029887.
  23. ^ Mahajan, S.; Williams, DF (junio de 1973). "Macleo por deformación en metales y aleaciones". International Metallurgical Reviews . 18 (2): 43–61. doi :10.1179/imtlr.1973.18.2.43.
  24. ^ Beyerlein, Irene J.; Mara, Nathan A.; Bhattacharyya, Dhriti; Alexander, David J.; Necker, Carl T. (enero de 2011). "Evolución de la textura mediante maclado combinado de deslizamiento y deformación en nanocompuestos eutécticos de plata y cobre laminados". Revista Internacional de Plasticidad . 27 (1): 121–146. doi :10.1016/j.ijplas.2010.05.007.
  25. ^ Courtney, Thomas H. (2000) Comportamiento mecánico de los materiales , 2.ª edición, McGraw Hill, ISBN 1-57766-425-6 
  26. ^ Nurul Akmal Che, Lah; Trigueros, Sonia (2019). "Síntesis y modelado de las propiedades mecánicas de nanocables de Ag, Au y Cu". Sci. Technol. Adv. Mater . 20 (1): 225–261. Bibcode :2019STAdM..20..225L. doi :10.1080/14686996.2019.1585145. PMC 6442207 . PMID  30956731. 
  27. ^ Steinmetz, DR; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed (2013), "Revelando el comportamiento de endurecimiento por deformación de aceros con plasticidad inducida por maclado: teoría, simulaciones, experimentos", Acta Materialia , 61 (2): 494, Bibcode :2013AcMat..61..494S, doi :10.1016/j.actamat.2012.09.064.
  28. ^ Christian, JW; Mahajan, S. (1995). "Macleo de deformación". Progreso en la ciencia de los materiales . 39 (1–2): 1–157. doi :10.1016/0079-6425(94)00007-7.
  29. ^ Calhoun, CA; Garlea, E.; Sisneros, TA; Agnew, SR (abril de 2018). "Caracterización por difracción de neutrones in situ de la deformación dependiente de la temperatura en uranio α". Journal of Nuclear Materials . 502 : 60–67. Bibcode :2018JNuM..502...60C. doi : 10.1016/j.jnucmat.2018.01.036 . OSTI  1478070.
  30. ^ Bilby, BA; Crocker, AG (26 de octubre de 1965). "La teoría de la cristalografía del maclado por deformación". Actas de la Royal Society de Londres. Serie A. Ciencias matemáticas y físicas . 288 (1413): 240–255. Bibcode :1965RSPSA.288..240B. doi :10.1098/rspa.1965.0216. ISSN  0080-4630. S2CID  120566509.
  31. ^ Cahn, RW (octubre de 1954). "Cristales maclados". Avances en Física . 3 (12): 363–445. Código Bibliográfico :1954AdPhy...3..363C. doi :10.1080/00018735400101223. ISSN  0001-8732.
  32. ^ Wang, S.; Schuman, C.; Bao, L.; Lecomte, JS; Zhang, Y.; Raulot, JM; Philippe, MJ; Zhao, X.; Esling, C. (mayo de 2012). "Criterio de selección de variantes para variantes gemelas en aleaciones de titanio deformadas por laminación" (PDF) . Acta Materialia . 60 (9): 3912–3919. Bibcode :2012AcMat..60.3912W. doi :10.1016/j.actamat.2012.03.046.
  33. ^ ab Christian, JW (2002). "Macleo de deformación". La teoría de las transformaciones en metales y aleaciones . Elsevier. págs. 859–960. doi :10.1016/b978-008044019-4/50025-8. ISBN 978-0-08-044019-4.
  34. ^ Abdolvand, Hamidreza; Sedaghat, Omid; Guo, Yi (octubre de 2018). "Nucleación y crecimiento de maclas { 11 2 2 } en titanio: campos de energía elástica y tensión en las proximidades de las maclas". Materialia . 2 : 58–62. doi :10.1016/j.mtla.2018.06.012. S2CID  139852253.
  35. ^ ab Guo, Y.; Schwiedrzik, J.; Michler, J.; Maeder, X. (1 de noviembre de 2016). "Sobre la nucleación y el crecimiento de la macla {112¯2} en titanio de pureza comercial: investigación in situ del campo de tensión local y la distribución de la densidad de dislocaciones". Acta Materialia . 120 : 292–301. doi :10.1016/j.actamat.2016.08.073. ISSN  1359-6454.
  36. ^ Paudel, YubRaj; Barrett, Christopher D.; Tschopp, Mark A.; Inal, Kaan; El Kadiri, Haitham (julio de 2017). "Más allá de la nucleación maclada inicial en metales hcp: formulación micromecánica para determinar el espaciamiento maclado durante la deformación". Acta Materialia . 133 : 134–146. Bibcode :2017AcMat.133..134P. doi : 10.1016/j.actamat.2017.05.013 . ISSN  1359-6454.
  37. ^ Paramatmuni, Chaitanya; Zheng, Zebang; Rainforth, W. Mark; Dunne, Fionn PE (1 de diciembre de 2020). "Nucleación gemela y selección de variantes en aleaciones de Mg: un modelo integrado de plasticidad cristalina y un enfoque experimental" (PDF) . Revista internacional de plasticidad . 135 : 102778. doi :10.1016/j.ijplas.2020.102778. ISSN  0749-6419. S2CID  224887964.
  38. ^ Paramatmuni, Chaitanya; Guo, Yi; Withers, Philip J.; Dunne, Fionn PE (1 de agosto de 2021). "Un estudio mecanicista tridimensional de los impulsores de la nucleación maclada clásica y la selección de variantes en aleaciones de Mg: un estudio experimental y de modelado a mesoescala". Revista internacional de plasticidad . 143 : 103027. doi :10.1016/j.ijplas.2021.103027. hdl : 10044/1/90290 . ISSN  0749-6419. S2CID  236612852.
  39. ^ Arul Kumar, M.; Beyerlein, IJ; Tomé, CN (1 de septiembre de 2016). "Efecto de los campos de tensión locales sobre las características gemelas de los metales HCP". Acta Materialia . 116 : 143-154. Código Bib : 2016AcMat.116..143A. doi : 10.1016/j.actamat.2016.06.042 . ISSN  1359-6454.
  40. ^ ab Beyerlein, Irene J.; Zhang, Xinghang; Misra, Amit (julio de 2014). "Gemelos de crecimiento y gemelos de deformación en metales". Revisión anual de investigación de materiales . 44 (1): 329–363. Bibcode :2014AnRMS..44..329B. doi : 10.1146/annurev-matsci-070813-113304 . ISSN  1531-7331.
  41. ^ ab Britton, TB; Dunne, FPE; Wilkinson, AJ (8 de junio de 2015). "Sobre la base mecanicista de la deformación a microescala en metales hexagonales compactos". Actas de la Royal Society A: Ciencias matemáticas, físicas e ingeniería . 471 (2178): 20140881. Bibcode :2015RSPSA.47140881B. doi : 10.1098/rspa.2014.0881 . S2CID  138085929.
  42. ^ Liu, Y.; Tang, PZ; Gong, MY; McCabe, RJ; Wang, J.; Tomé, CN (25 de julio de 2019). "Carácter tridimensional de la macla de deformación en magnesio". Nature Communications . 10 (1): 3308. Bibcode :2019NatCo..10.3308L. doi :10.1038/s41467-019-10573-7. ISSN  2041-1723. PMC 6658514 . PMID  31346160. 
  43. ^ Barnett, MR (25 de agosto de 2007). "Macleo y ductilidad de aleaciones de magnesio: Parte I: Macleos de "tensión"". Ciencia e ingeniería de materiales: A . 464 (1): 1–7. doi :10.1016/j.msea.2006.12.037. ISSN  0921-5093.
  44. ^ Arul Kumar, M.; Kanjarla, Alaska; Niezgoda, SR; Lebensohn, RA; Tomé, CN (1 de febrero de 2015). "Estudio numérico del estado tensional de una gemela de deformación en magnesio". Acta Materialia . 84 : 349–358. doi : 10.1016/j.actamat.2014.10.048 . ISSN  1359-6454.
  45. ^ ab Koko, Abdalrhaman; Elmukashfi, Elsiddig; Dragnevski, Kalin; Wilkinson, Angus J.; Marrow, Thomas James (1 de octubre de 2021). "Análisis J-integral de los campos de deformación elástica de los maclados de deformación de ferrita utilizando difracción de retrodispersión de electrones". Acta Materialia . 218 : 117203. Bibcode :2021AcMat.21817203K. doi :10.1016/j.actamat.2021.117203. ISSN  1359-6454.
  46. ^ Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, DM; Wilkinson, AJ; Bagot, PAJ; Moody, MP; Atkinson, C.; Jérusalem, A.; Reed, RC (15 de agosto de 2017). "Sobre el mecanismo de micromaclado en una superaleación monocristalina". Acta Materialia . 135 : 314–329. Bibcode :2017AcMat.135..314B. doi : 10.1016/j.actamat.2017.05.072 . hdl : 10044/1/63276 . ISSN  1359-6454. S2CID  55924981.
  47. ^ ab Mahajan, S.; Williams, DF (1973-06-01). "Macleo por deformación en metales y aleaciones". International Metallurgical Reviews . 18 (2): 43–61. doi :10.1179/imtlr.1973.18.2.43. ISSN  0367-9020.
  48. ^ Beyerlein, IJ; Capolungo, L.; Marshall, PE; McCabe, RJ; Tomé, CN (28 de mayo de 2010). "Análisis estadísticos del maclado por deformación en magnesio". Revista filosófica . 90 (16): 2161–2190. Bibcode :2010PMag...90.2161B. doi :10.1080/14786431003630835. ISSN  1478-6435. S2CID  136111937.
  49. ^ ab Lloyd, JT (28 de febrero de 2018). "Un modelo basado en dislocaciones para el crecimiento gemelo dentro y a través de granos". Actas de la Royal Society A: Ciencias matemáticas, físicas e ingeniería . 474 (2210): 20170709. Bibcode :2018RSPSA.47470709L. doi :10.1098/rspa.2017.0709. PMC 5832837 . PMID  29507516. 
  50. ^ Venables, JA (1961-03-01). "Macleo de deformación en metales cúbicos centrados en las caras". Revista filosófica . 6 (63): 379–396. Bibcode :1961PMag....6..379V. doi :10.1080/14786436108235892. ISSN  0031-8086.
  51. ^ Johansson, Johan; Odén, Magnus (1 de junio de 2000). "Reparto de carga entre austenita y ferrita en un acero inoxidable dúplex durante la carga cíclica". Metallurgical and Materials Transactions A . 31 (6): 1557–1570. Bibcode :2000MMTA...31.1557J. doi :10.1007/s11661-000-0166-3. ISSN  1543-1940. S2CID  137142133.
  52. ^ Marrow, TJ; King, JE (15 de junio de 1994). "Mecanismos de propagación de grietas por fatiga en un acero inoxidable dúplex envejecido térmicamente". Ciencia e ingeniería de materiales: A . 183 (1): 91–101. doi :10.1016/0921-5093(94)90893-1. ISSN  0921-5093.
  53. ^ Christian, JW; Mahajan, S. (1 de enero de 1995). "Macleo de deformación". Progreso en la ciencia de los materiales . 39 (1): 1–157. doi :10.1016/0079-6425(94)00007-7. ISSN  0079-6425.
  54. ^ Sleeswyk, A. W (1 de agosto de 1962). "Dislocaciones emisarias: teoría y experimentos sobre la propagación de maclas de deformación en hierro α". Acta Metallurgica . 10 (8): 705–725. doi :10.1016/0001-6160(62)90040-8. ISSN  0001-6160.
  55. ^ Spreadborough, J.; Langheinrich, D.; Anderson, E.; Brandon, D. (diciembre de 1964). "Observaciones de la formación de hoyos de grabado en relación con las maclas en hierro y aleaciones de hierro". Revista de Física Aplicada . 35 (12): 3585–3587. Bibcode :1964JAP....35.3585S. doi :10.1063/1.1713275. ISSN  0021-8979.
  56. ^ Guo, Y.; Abdolvand, H.; Britton, TB; Wilkinson, AJ (1 de marzo de 2017). "Crecimiento de maclas {1122} en titanio: una investigación combinada experimental y de modelado del estado local de deformación". Acta Materialia . 126 : 221–235. doi : 10.1016/j.actamat.2016.12.066 . hdl : 10044/1/67478 . ISSN  1359-6454. S2CID  136128910.
  57. ^ Baxevanakis, KP; Gourgiotis, PA; Georgiadis, HG (julio de 2017). "Interacción de grietas con dislocaciones en elasticidad de par-esfuerzo. Parte I: modo de apertura". Revista internacional de sólidos y estructuras . 118–119: 179–191. doi : 10.1016/j.ijsolstr.2017.03.019 . ISSN  0020-7683. S2CID  55155535.
  58. ^ ab Kacher, Josh; Sabisch, Julián E.; Menor, Andrew M. (1 de julio de 2019). "Análisis estadístico de interacciones entre límites de grano y gemelos en renio puro". Acta Materialia . 173 : 44–51. Código Bib : 2019AcMat.173...44K. doi : 10.1016/j.actamat.2019.04.051 . ISSN  1359-6454.
  59. ^ Gong, Mingyu; Hirth, John P.; Liu, Yue; Shen, Yao; Wang, Jian (3 de noviembre de 2017). "Estructuras de interfaz y mecanismos de maclado de maclas en metales hexagonales". Materials Research Letters . 5 (7): 449–464. doi : 10.1080/21663831.2017.1336496 . S2CID  136448819.
  60. ^ Wang, Yunzhi; Li, Ju (1 de febrero de 2010). "Modelado de defectos y deformaciones mediante campos de fase". Acta Materialia . 58 (4): 1212–1235. Bibcode :2010AcMat..58.1212W. doi :10.1016/j.actamat.2009.10.041. ISSN  1359-6454.
  61. ^ Eshelby, John Douglas; Mott, Nevill Francis (6 de noviembre de 1951). "La fuerza sobre una singularidad elástica". Philosophical Transactions of the Royal Society of London. Serie A, Ciencias matemáticas y físicas . 244 (877): 87–112. Bibcode :1951RSPTA.244...87E. doi :10.1098/rsta.1951.0016. S2CID  14703976.
  62. ^ Rice, JR (1968-06-01). "Una integral independiente de la trayectoria y el análisis aproximado de la concentración de la deformación por entalladuras y grietas". Journal of Applied Mechanics . 35 (2): 379–386. Bibcode :1968JAM....35..379R. doi :10.1115/1.3601206. ISSN  0021-8936.
  63. ^ Venables, J. A (1 de julio de 1964). "La microscopía electrónica del maclado por deformación". Revista de Física y Química de Sólidos . 25 (7): 685–692. Bibcode :1964JPCS...25..685V. doi :10.1016/0022-3697(64)90177-5. ISSN  0022-3697.

Fuentes

Enlaces externos