

En matemáticas , la intersección de dos o más objetos es otro objeto que consiste en todo lo que está contenido en todos los objetos simultáneamente. Por ejemplo, en geometría euclidiana , cuando dos líneas en un plano no son paralelas, su intersección es el punto en el que se encuentran. De manera más general, en la teoría de conjuntos , la intersección de conjuntos se define como el conjunto de elementos que pertenecen a todos ellos. A diferencia de la definición euclidiana, esta no presupone que los objetos en consideración se encuentren en un espacio común .
La intersección es uno de los conceptos básicos de la geometría . Una intersección puede tener varias formas geométricas , pero un punto es la más común en una geometría plana . La geometría de incidencia define una intersección (generalmente, de planos ) como un objeto de dimensión inferior que es incidente a cada uno de los objetos originales. En este enfoque, una intersección a veces puede no estar definida, como en el caso de las líneas paralelas . En ambos casos, el concepto de intersección se basa en la conjunción lógica . La geometría algebraica define las intersecciones a su manera con la teoría de la intersección .
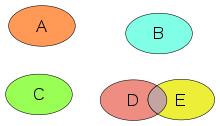
Puede haber más de un objeto primitivo, como puntos (en la imagen de arriba), que formen una intersección. La intersección se puede considerar colectivamente como todos los objetos compartidos (es decir, la operación de intersección da como resultado un conjunto , posiblemente vacío), o como varios objetos de intersección ( posiblemente cero ).

La intersección de dos conjuntos A y B es el conjunto de elementos que están tanto en A como en B. Formalmente,
Por ejemplo, si y , entonces . Un ejemplo más elaborado (que involucra conjuntos infinitos) es:
Como otro ejemplo, el número 5 no está contenido en la intersección del conjunto de números primos {2, 3, 5, 7, 11, …} y el conjunto de números pares {2, 4, 6, 8, 10, …} , porque aunque 5 es un número primo, no es par. De hecho, el número 2 es el único número en la intersección de estos dos conjuntos. En este caso, la intersección tiene un significado matemático: el número 2 es el único número primo par.

En geometría , una intersección es un punto, una línea o una curva común a dos o más objetos (como líneas, curvas, planos y superficies). El caso más simple en geometría euclidiana es la intersección línea-línea entre dos líneas distintas , que es un punto (a veces llamado vértice ) o no existe (si las líneas son paralelas ). Otros tipos de intersección geométrica incluyen:
La intersección se denota por U+2229 ∩ INTERSECCIÓN de Operadores matemáticos Unicode .
El símbolo U+2229 ∩ INTERSECTION fue utilizado por primera vez por Hermann Grassmann en Die Ausdehnungslehre von 1844 como símbolo de operación general, no especializado para intersección. A partir de ahí, fue utilizado por Giuseppe Peano (1858-1932) para intersección, en 1888 en Calcolo geométrico secondo l'Ausdehnungslehre di H. Grassmann . [2] [3]
Peano también creó los símbolos grandes para la intersección general y la unión de más de dos clases en su libro Formulario matemático de 1908. [4] [5]