Grupo ortogonal proyectivo

En geometría proyectiva y álgebra lineal , el grupo ortogonal proyectivo PO es la acción inducida del grupo ortogonal de un espacio cuadrático V = ( V , Q ) ^{[nota 1]} sobre el espacio proyectivo asociado P( V ). Explícitamente, el grupo ortogonal proyectivo es el grupo cociente

PO( V ) = O( V )/ZO( V ) = O( V )/{± I }

donde O( V ) es el grupo ortogonal de ( V ) y ZO( V )={± I } es el subgrupo de todas las transformaciones escalares ortogonales de V – estas consisten en la identidad y la reflexión a través del origen . Estos escalares se cocienten porque actúan trivialmente en el espacio proyectivo y forman el núcleo de la acción, y la notación "Z" se debe a que las transformaciones escalares son el centro del grupo ortogonal.

El grupo ortogonal especial proyectivo , PSO, se define de manera análoga, como la acción inducida del grupo ortogonal especial sobre el espacio proyectivo asociado. Explícitamente:

PSO( V ) = SO( V )/ZSO( V )

donde SO( V ) es el grupo ortogonal especial sobre V y ZSO( V ) es el subgrupo de transformaciones escalares ortogonales con determinante unitario . Aquí ZSO es el centro de SO, y es trivial en dimensión impar, mientras que es igual a {±1} en dimensión par – esta distinción impar/par ocurre en toda la estructura de los grupos ortogonales. Por analogía con GL/SL y GO/SO, el grupo ortogonal proyectivo también se denomina a veces grupo ortogonal general proyectivo y se denota PGO.

Al igual que el grupo ortogonal, el grupo ortogonal proyectivo puede definirse sobre cualquier cuerpo y con diversas formas cuadráticas, aunque, al igual que con el grupo ortogonal ordinario, el énfasis principal está en el grupo ortogonal proyectivo definido positivo real ; otros cuerpos se desarrollan en generalizaciones, más adelante. Salvo que se mencione lo contrario, en lo sucesivo PO y PSO se referirán a los grupos definidos positivos reales.

Al igual que los grupos de espín y los grupos de pines , que son cubiertas en lugar de cocientes de los grupos ortogonales (especiales), los grupos ortogonales proyectivos (especiales) son de interés para los análogos geométricos (proyectivos) de la geometría euclidiana, como grupos de Lie relacionados , y en la teoría de la representación .

De manera más intrínseca, el grupo ortogonal proyectivo (definido positivo real) PO puede definirse como las isometrías del espacio elíptico (en el sentido de geometría elíptica ), mientras que PSO puede definirse como las isometrías que preservan la orientación del espacio elíptico (cuando el espacio es orientable; de ​​lo contrario PSO = PO).

Estructura

Dimensiones pares e impares

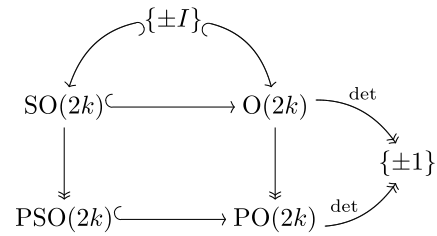
La estructura de PO difiere significativamente entre dimensión par e impar, fundamentalmente porque en dimensión par, la reflexión a través del origen preserva la orientación, mientras que en dimensión impar la invierte ( pero ). Esto se ve en el hecho de que cada espacio proyectivo real de dimensión impar es orientable, mientras que cada espacio proyectivo real de dimensión par de dimensión positiva es no orientable. En un nivel más abstracto, las álgebras de Lie de grupos ortogonales proyectivos de dimensión par e impar forman dos familias diferentes: ${\displaystyle -I\in \operatorname {SO} (2k)}$ ${\displaystyle -I\not \in \operatorname {SO} (2k+1)}$ ${\displaystyle B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.}$

Por lo tanto, O(2 k +1) = SO(2 k +1) × {± I }, ^{[nota 2]} mientras que y es en cambio una extensión central no trivial de PO(2 k ). ${\displaystyle \operatorname {O} (2k)\neq \operatorname {SO} (2k)\times \{\pm I\}}$

Tenga en cuenta que PO(2 k +1) son isometrías de R P ^{2 k} = P( R ^{2 k +1} ), mientras que PO(2 k ) son isometrías de R P ^{2 k −1} = P( R ^{2 k} ) – el grupo de dimensión impar (vector) son isometrías del espacio proyectivo de dimensión par, mientras que el grupo de dimensión par (vector) son isometrías del espacio proyectivo de dimensión impar.

En dimensión impar, ^{[nota 3]} entonces el grupo de isometrías proyectivas puede identificarse con el grupo de isometrías rotacionales. ${\displaystyle \operatorname {SO} (2k+1)\cong \operatorname {PSO} (2k+1)=\operatorname {PO} (2k+1),}$

En dimensión par, SO(2 k ) → PSO(2 k ) y O(2 k ) → PO(2 k ) son ambos recubrimientos de 2 a 1, y PSO(2 k ) < PO(2 k ) es un subgrupo de índice 2.

Propiedades generales

PSO y PO no tienen centro , al igual que PSL y PGL; esto se debe a que las matrices escalares no solo son el centro de SO y O, sino también el hipercentro (el cociente por el centro no siempre produce un grupo sin centro).

PSO es el subgrupo maximal compacto en el grupo lineal especial proyectivo PSL, mientras que PO es maximal compacto en el grupo lineal general proyectivo PGL. Esto es análogo a que SO sea maximal compacto en SL y que O sea maximal compacto en GL.

Teoría de la representación

PO es de interés básico en la teoría de la representación: un homomorfismo de grupo G  → PGL se llama representación proyectiva de G, así como una función G  → GL se llama representación lineal de G , y así como cualquier representación lineal puede reducirse a una función G  → O (tomando un producto interno invariante), cualquier representación proyectiva puede reducirse a una función G  → PO.

Véase grupo lineal proyectivo: teoría de la representación para mayor discusión.

Subgrupos

Los subgrupos del grupo ortogonal proyectivo corresponden a subgrupos del grupo ortogonal que contienen − I (que tienen simetría central ). Como siempre con una función cociente (por el teorema de red ), hay una conexión de Galois entre subgrupos de O y PO, donde la adjunción en O (dada al tomar la imagen en PO y luego la preimagen en O) simplemente agrega − I si está ausente.

De particular interés son los subgrupos discretos, que pueden realizarse como simetrías de politopos proyectivos ; estos corresponden a los grupos puntuales (discretos) que incluyen simetría central. Compárese con los subgrupos discretos del grupo Spin , particularmente el caso tridimensional de los grupos poliédricos binarios .

Por ejemplo, en 3 dimensiones, 4 de los 5 sólidos platónicos tienen simetría central (cubo/octaedro, dodecaedro/icosaedro), mientras que el tetraedro no; sin embargo, el octaedro estrellado tiene simetría central, aunque el grupo de simetría resultante es el mismo que el del cubo/octaedro.

Topología

PO y PSO, como grupos topológicos sin centro, se encuentran en la parte inferior de una secuencia de grupos de cobertura , cuya parte superior son los grupos Pin ( simplemente conexos ) o el grupo Spin , respectivamente:

Pin _± ( n ) → O ( n ) → PO ( n ).

Espín( n ) → SO( n ) → PSO( n ).

Todos estos grupos son formas reales compactas del mismo álgebra de Lie.

Todas estas son coberturas de 2 a 1, excepto SO(2 k +1) → PSO(2 k +1) que es de 1 a 1 (un isomorfismo).

Grupos de homotopía

Los grupos de homotopía anteriores no cambian bajo cubierta, por lo que concuerdan con los del grupo ortogonal. Los grupos de homotopía inferiores se dan a continuación. ${\displaystyle \pi _{1}}$

${\displaystyle \pi _{0}(\operatorname {PSO} )\cong 1}$

${\displaystyle \pi _{0}(\operatorname {PO} (2k))\cong \mathbf {Z} /2\mathbf {Z} ,\pi _{0}(\operatorname {PO} (2k+1))\cong 1.}$

El grupo fundamental de PSO( n ) (sin centro) es igual al centro de Spin( n ) (simplemente conexo ), lo que siempre es cierto acerca de los grupos de cobertura:

${\displaystyle \pi _{1}(\operatorname {PSO} (n))=\pi _{1}(\operatorname {PO} (n))=\operatorname {Z} (\operatorname {Spin} (n)).}$

Utilizando la tabla de centros de los grupos de espín se obtiene (para ): ${\displaystyle k\geq 1}$

${\displaystyle \pi _{1}(\operatorname {PSO} (4k))=\mathbf {Z} /2\mathbf {Z} \oplus \mathbf {Z} /2\mathbf {Z} ,}$

${\displaystyle \pi _{1}(\operatorname {PSO} (4k+2))=\mathbf {Z} /4\mathbf {Z} ,}$

${\displaystyle \pi _{1}(\operatorname {PSO} (2k+1))=\pi _{1}(\operatorname {SO} (2k+1))=\mathbf {Z} /2\mathbf {Z} ,}$

En bajas dimensiones:

${\displaystyle \pi _{1}(\operatorname {PSO} (1))=1,}$Como el grupo es trivial.

${\displaystyle \pi _{1}(\operatorname {PSO} (2))=\mathbf {Z} ,}$ya que topológicamente es un círculo, aunque tenga en cuenta que la preimagen de la identidad en Spin(2) es como para otros ${\displaystyle \mathbf {Z} /4\mathbf {Z} ,}$ ${\displaystyle 4k+2.}$

Grupos de homología

Paquetes

Así como el grupo ortogonal es el grupo de estructura de los fibrados vectoriales , el grupo ortogonal proyectivo es el grupo de estructura de los fibrados proyectivos , y el espacio de clasificación correspondiente se denota BPO.

Generalizaciones

Al igual que el grupo ortogonal, el grupo ortogonal proyectivo se puede generalizar de dos formas principales: cambiando el cuerpo o cambiando la forma cuadrática. Además de los números reales, el interés principal está en los números complejos o cuerpos finitos, mientras que (sobre los reales) las formas cuadráticas también pueden ser formas indefinidas y se denotan PO( p , q ) por su signatura.

El grupo ortogonal proyectivo complejo, PO( n , C ) no debe confundirse con el grupo unitario proyectivo , PU( n ): PO conserva una forma simétrica, mientras que PU conserva una forma hermítica – PU son las simetrías del espacio proyectivo complejo (preservando la métrica de Fubini-Study ).

En los campos de característica 2 hay complicaciones añadidas: las formas cuadráticas y las formas bilineales simétricas ya no son equivalentes, I = − I , y el determinante debe sustituirse por el invariante de Dickson .

Campos finitos

El grupo ortogonal proyectivo sobre un cuerpo finito se utiliza en la construcción de una familia de grupos finitos simples de tipo Lie , a saber, los grupos de Chevalley de tipo D _n . El grupo ortogonal sobre un cuerpo finito, O( n , q ) no es simple, ya que tiene a SO como subgrupo y un centro no trivial ({± I }) (de ahí PO como cociente). Ambos se fijan al pasar a PSO, pero PSO en sí mismo no es en general simple, y en su lugar se debe utilizar un subgrupo (que puede ser de índice 1 o 2), definido por la norma de espinor (en característica impar) o el cuasideterminante (en característica par). ^[1] El cuasideterminante se puede definir como (−1) ^D , donde D es el invariante de Dickson (es el determinante definido por el invariante de Dickson), o en términos de la dimensión del espacio fijo.

Notas

1. Un espacio cuadrático es un espacio vectorial V junto con una forma cuadrática Q ; la Q se elimina de la notación cuando está claro.
2. Este producto es una suma directa interna –un producto de subgrupos–, no simplemente una suma directa externa abstracta .
3. La distinción entre isomorfismo e igualdad en esta ecuación se debe a que el contexto es la función cociente 2 a 1 O → PO – PSO(2 k +1) y PO(2 k +1) son subconjuntos iguales del objetivo (es decir, todo el espacio), de ahí la igualdad, mientras que la función inducida SO → PSO es un isomorfismo, pero los dos grupos son subconjuntos de espacios diferentes, de ahí el isomorfismo en lugar de una igualdad. Véase (Conway & Smith 2003, p. 34) para un ejemplo de esta distinción.

Véase también

• Grupo lineal proyectivo
• Grupo unitario proyectivo
• Grupo ortogonal
• Grupo de spinning

Referencias

1. ATLAS , pág. xi

• Conway, John Horton ; Smith, Derek Alan (2003-02-07), "3.7 Los grupos proyectivos o elípticos", Sobre cuaterniones y octoniones , AK Peters, Ltd., págs. 34, ISBN 978-1-56881-134-5
• Conway, JH; Curtis, RT; Norton, SP; Parker, RA; y Wilson, RA "Los grupos GO _n ( q ), SO _n ( q ), PGO _n ( q ), y PSO _n ( q ), y O _n ( q )." §2.4 en Atlas de grupos finitos: subgrupos máximos y caracteres ordinarios para grupos simples. Oxford, Inglaterra: Clarendon Press, págs. xi–xii, 1985.

Enlaces externos

• Weisstein, Eric W. "Grupo ortogonal general proyectivo". MathWorld .
• Weisstein, Eric W. "Grupo ortogonal especial proyectivo". MathWorld .