
El gas es uno de los cuatro estados fundamentales de la materia . Los otros son sólido , líquido y plasma . [1] Un gas puro puede estar formado por átomos individuales (por ejemplo, un gas noble como el neón ), moléculas elementales formadas por un tipo de átomo (por ejemplo, oxígeno ) o moléculas compuestas formadas por una variedad de átomos (por ejemplo, dióxido de carbono ). Una mezcla de gases , como el aire , contiene una variedad de gases puros. Lo que distingue a los gases de los líquidos y sólidos es la gran separación de las partículas de gas individuales . Esta separación generalmente hace que un gas incoloro sea invisible para el observador humano.
El estado gaseoso de la materia se encuentra entre los estados líquido y plasmático, [2] este último proporciona el límite superior de temperatura para los gases. En el extremo inferior de la escala de temperatura se encuentran los gases cuánticos degenerativos [3] que están ganando cada vez más atención. [4] Los gases atómicos de alta densidad superenfriados a temperaturas muy bajas se clasifican por su comportamiento estadístico como gases de Bose o gases de Fermi . Para obtener una lista completa de estos estados exóticos de la materia, consulte la lista de estados de la materia .
Los únicos elementos químicos que son gases moleculares homonucleares diatómicos estables en condiciones normales son el hidrógeno (H 2 ), el nitrógeno (N 2 ), el oxígeno (O 2 ) y dos halógenos : flúor (F 2 ) y cloro (Cl 2 ). Cuando se agrupan con los gases nobles monoatómicos – helio (He), neón (Ne), argón (Ar), criptón (Kr), xenón (Xe) y radón (Rn) – estos gases se denominan “gases elementales”.
La palabra gas fue utilizada por primera vez por el químico flamenco de principios del siglo XVII Jan Baptist van Helmont . [5] Identificó el dióxido de carbono , el primer gas conocido distinto del aire. [6] La palabra de Van Helmont parece haber sido simplemente una transcripción fonética de la palabra griega antigua χάος ' caos ' - la g en holandés se pronuncia como ch en " loch " (fricativa velar sorda, / x / ) - en cuyo caso Van Helmont simplemente estaba siguiendo el uso alquímico establecido atestiguado por primera vez en las obras de Paracelso . Según la terminología de Paracelso, caos significaba algo así como ' agua ultra enrarecida ' . [7]
Una versión alternativa es que el término de Van Helmont se deriva de " gahst (o geist ), que significa fantasma o espíritu". [8] Los editores del Oxford English Dictionary no le dan crédito a esa versión . [9] Por el contrario, el historiador franco-estadounidense Jacques Barzun especuló que Van Helmont había tomado prestada la palabra del alemán Gäscht , que significa la espuma resultante de la fermentación . [10]
Debido a que la mayoría de los gases son difíciles de observar directamente, se describen mediante el uso de cuatro propiedades físicas o características macroscópicas : presión , volumen , número de partículas (los químicos las agrupan por moles ) y temperatura. Estas cuatro características fueron observadas repetidamente por científicos como Robert Boyle , Jacques Charles , John Dalton , Joseph Gay-Lussac y Amedeo Avogadro para una variedad de gases en varios entornos. Sus estudios detallados finalmente llevaron a una relación matemática entre estas propiedades expresada por la ley de los gases ideales (ver § Sección de gases ideales y perfectos a continuación).
Las partículas de gas están muy separadas entre sí y, en consecuencia, tienen enlaces intermoleculares más débiles que los líquidos o sólidos. Estas fuerzas intermoleculares resultan de interacciones electrostáticas entre partículas de gas. Las áreas con carga similar de diferentes partículas de gas se repelen, mientras que las regiones con carga opuesta de diferentes partículas de gas se atraen entre sí; los gases que contienen iones cargados permanentemente se conocen como plasmas . Los compuestos gaseosos con enlaces covalentes polares contienen desequilibrios de carga permanentes y, por lo tanto, experimentan fuerzas intermoleculares relativamente fuertes, aunque la carga neta del compuesto permanece neutra. Existen cargas transitorias inducidas aleatoriamente a través de enlaces covalentes no polares de moléculas y las interacciones electrostáticas causadas por ellas se conocen como fuerzas de Van der Waals . La interacción de estas fuerzas intermoleculares varía dentro de una sustancia, lo que determina muchas de las propiedades físicas únicas de cada gas. [11] [12] Una comparación de los puntos de ebullición de los compuestos formados por enlaces iónicos y covalentes nos lleva a esta conclusión. [13]
En comparación con los demás estados de la materia, los gases tienen una densidad y una viscosidad bajas . La presión y la temperatura influyen en las partículas dentro de un determinado volumen. Esta variación en la separación y la velocidad de las partículas se denomina compresibilidad . Esta separación y tamaño de las partículas influye en las propiedades ópticas de los gases, como se puede comprobar en la siguiente lista de índices de refracción . Por último, las partículas de los gases se dispersan o difunden para distribuirse de forma homogénea por todo el recipiente que las contiene.
Al observar un gas, es habitual especificar un marco de referencia o escala de longitud . Una escala de longitud mayor corresponde a un punto de vista macroscópico o global del gas. Esta región (denominada volumen) debe tener un tamaño suficiente para contener una gran muestra de partículas de gas. El análisis estadístico resultante de este tamaño de muestra produce el comportamiento "promedio" (es decir, velocidad, temperatura o presión) de todas las partículas de gas dentro de la región. Por el contrario, una escala de longitud menor corresponde a un punto de vista microscópico o de partículas.
Macroscópicamente, las características de los gases que se miden se refieren a las partículas de gas en sí (velocidad, presión o temperatura) o a su entorno (volumen). Por ejemplo, Robert Boyle estudió química neumática durante una pequeña parte de su carrera. Uno de sus experimentos relacionó las propiedades macroscópicas de la presión y el volumen de un gas. En su experimento utilizó un manómetro de tubo en J que parece un tubo de ensayo con la forma de la letra J. Boyle atrapó un gas inerte en el extremo cerrado del tubo de ensayo con una columna de mercurio , haciendo así que el número de partículas y la temperatura fueran constantes. Observó que cuando se aumentaba la presión en el gas, añadiendo más mercurio a la columna, el volumen del gas atrapado disminuía (esto se conoce como relación inversa ). Además, cuando Boyle multiplicaba la presión y el volumen de cada observación, el producto era constante. Esta relación se mantenía para cada gas que Boyle observaba, lo que condujo a la ley (PV=k), llamada así en honor a su trabajo en este campo.

Existen muchas herramientas matemáticas disponibles para analizar las propiedades de los gases. El equipo de laboratorio de Boyle permitió utilizar un cálculo simple para obtener sus resultados analíticos. Sus resultados fueron posibles porque estaba estudiando gases en situaciones de presión relativamente baja donde se comportaban de una manera "ideal". Estas relaciones ideales se aplican a los cálculos de seguridad para una variedad de condiciones de vuelo en los materiales en uso. Sin embargo, el equipo de alta tecnología que se utiliza hoy en día fue diseñado para ayudarnos a explorar de manera segura los entornos operativos más exóticos donde los gases ya no se comportan de una manera "ideal". A medida que los gases se someten a condiciones extremas, las herramientas para interpretarlas se vuelven más complejas, desde las ecuaciones de Euler para el flujo no viscoso hasta las ecuaciones de Navier-Stokes [14] que tienen en cuenta completamente los efectos viscosos. Esta matemática avanzada, que incluye estadísticas y cálculo multivariable , adaptada a las condiciones del sistema de gas en cuestión, hace posible resolver situaciones dinámicas tan complejas como la reentrada de un vehículo espacial. Un ejemplo es el análisis de la reentrada del transbordador espacial que se muestra en la imagen para garantizar que las propiedades del material en esta condición de carga sean apropiadas. En esta situación de vuelo, el gas ya no se comporta de forma ideal.
El símbolo utilizado para representar la presión en las ecuaciones es "p" o "P" con unidades SI de pascales .

Al describir un recipiente con gas, el término presión (o presión absoluta) se refiere a la fuerza promedio por unidad de área que el gas ejerce sobre la superficie del recipiente. Dentro de este volumen, a veces es más fácil visualizar las partículas de gas moviéndose en línea recta hasta que chocan con el recipiente (ver diagrama en la parte superior). La fuerza impartida por una partícula de gas en el recipiente durante esta colisión es el cambio en el momento de la partícula. [15] Durante una colisión, solo cambia el componente normal de la velocidad. Una partícula que viaja paralela a la pared no cambia su momento. Por lo tanto, la fuerza promedio sobre una superficie debe ser el cambio promedio en el momento lineal de todas estas colisiones de partículas de gas.
La presión es la suma de todos los componentes normales de fuerza ejercida por las partículas que impactan las paredes del recipiente dividida por el área de superficie de la pared.
El símbolo utilizado para representar la temperatura en las ecuaciones es T con unidades SI de kelvin .
La velocidad de una partícula de gas es proporcional a su temperatura absoluta . El volumen del globo en el video se encoge cuando las partículas de gas atrapadas disminuyen su velocidad con la adición de nitrógeno extremadamente frío. La temperatura de cualquier sistema físico está relacionada con los movimientos de las partículas (moléculas y átomos) que componen el sistema [gas]. [16] En mecánica estadística , la temperatura es la medida de la energía cinética promedio almacenada en una molécula (también conocida como energía térmica). Los métodos de almacenamiento de esta energía están dictados por los grados de libertad de la propia molécula ( modos de energía ). La energía térmica (cinética) añadida a un gas o líquido (un proceso endotérmico ) produce movimiento traslacional, rotacional y vibracional. Por el contrario, un sólido solo puede aumentar su energía interna excitando modos vibracionales adicionales, ya que la estructura de red cristalina impide tanto el movimiento traslacional como el rotacional. Estas moléculas de gas calentadas tienen un mayor rango de velocidad (distribución más amplia de velocidades) con una velocidad promedio o media más alta . La varianza de esta distribución se debe a que las velocidades de las partículas individuales varían constantemente, debido a las colisiones repetidas con otras partículas. El rango de velocidad se puede describir mediante la distribución de Maxwell-Boltzmann . El uso de esta distribución implica gases ideales cerca del equilibrio termodinámico para el sistema de partículas en consideración.
El símbolo utilizado para representar el volumen específico en las ecuaciones es "v" con unidades SI de metros cúbicos por kilogramo.
El símbolo utilizado para representar el volumen en las ecuaciones es "V" con unidades SI de metros cúbicos.
Al realizar un análisis termodinámico , es típico hablar de propiedades intensivas y extensivas . Las propiedades que dependen de la cantidad de gas (ya sea en masa o volumen) se denominan propiedades extensivas , mientras que las propiedades que no dependen de la cantidad de gas se denominan propiedades intensivas. El volumen específico es un ejemplo de una propiedad intensiva porque es la relación del volumen ocupado por una unidad de masa de un gas que es idéntico en todo un sistema en equilibrio. [17] 1000 átomos de un gas ocupan el mismo espacio que cualquier otro 1000 átomos para cualquier temperatura y presión dadas. Este concepto es más fácil de visualizar para sólidos como el hierro que son incompresibles en comparación con los gases. Sin embargo, el volumen en sí mismo --- no específico --- es una propiedad extensiva.
El símbolo que se utiliza para representar la densidad en las ecuaciones es ρ (rho), con unidades del SI de kilogramos por metro cúbico. Este término es el recíproco del volumen específico.
Dado que las moléculas de gas pueden moverse libremente dentro de un recipiente, su masa normalmente se caracteriza por la densidad. La densidad es la cantidad de masa por unidad de volumen de una sustancia, o la inversa del volumen específico. Para los gases, la densidad puede variar en un amplio rango porque las partículas son libres de acercarse entre sí cuando están limitadas por la presión o el volumen. Esta variación de la densidad se conoce como compresibilidad . Al igual que la presión y la temperatura, la densidad es una variable de estado de un gas y el cambio de densidad durante cualquier proceso está regido por las leyes de la termodinámica. Para un gas estático , la densidad es la misma en todo el recipiente. Por lo tanto, la densidad es una cantidad escalar . Se puede demostrar mediante la teoría cinética que la densidad es inversamente proporcional al tamaño del recipiente en el que está confinada una masa fija de gas. En este caso de una masa fija, la densidad disminuye a medida que aumenta el volumen.
Si pudiéramos observar un gas con un microscopio potente, veríamos un conjunto de partículas sin forma ni volumen definidos que se mueven de forma más o menos aleatoria. Estas partículas de gas solo cambian de dirección cuando chocan con otra partícula o con las paredes del recipiente que las contiene. Esta visión microscópica del gas está bien descrita por la mecánica estadística , pero puede describirse mediante muchas teorías diferentes. La teoría cinética de los gases , que supone que estas colisiones son perfectamente elásticas , no tiene en cuenta las fuerzas intermoleculares de atracción y repulsión.
La teoría cinética permite comprender mejor las propiedades macroscópicas de los gases al considerar su composición molecular y su movimiento. A partir de las definiciones de momento y energía cinética , [18] se pueden utilizar la conservación del momento y las relaciones geométricas de un cubo para relacionar las propiedades macroscópicas del sistema de temperatura y presión con la propiedad microscópica de la energía cinética por molécula. La teoría proporciona valores promedio para estas dos propiedades.
La teoría cinética de los gases puede ayudar a explicar cómo el sistema (el conjunto de partículas de gas en cuestión) responde a los cambios de temperatura, con un cambio correspondiente en la energía cinética .
Por ejemplo: imagina que tienes un recipiente sellado de un tamaño fijo (un volumen constante ), que contiene un número fijo de partículas de gas; comenzando desde el cero absoluto (la temperatura teórica a la que los átomos o moléculas no tienen energía térmica, es decir, no se mueven ni vibran), comienzas a agregar energía al sistema calentando el recipiente, de modo que la energía se transfiera a las partículas en el interior. Una vez que su energía interna está por encima de la energía del punto cero , lo que significa que su energía cinética (también conocida como energía térmica ) es distinta de cero, las partículas de gas comenzarán a moverse alrededor del recipiente. A medida que la caja se calienta más (a medida que se agrega más energía), las partículas individuales aumentan su velocidad promedio a medida que aumenta la energía interna total del sistema. La mayor velocidad promedio de todas las partículas conduce a una mayor tasa de colisiones (es decir, mayor número de colisiones por unidad de tiempo), entre las partículas y el recipiente, así como entre las partículas mismas.
La cantidad macroscópica y medible de presión es el resultado directo de estas colisiones de partículas microscópicas con la superficie, sobre las cuales las moléculas individuales ejercen una pequeña fuerza, cada una de las cuales contribuye a la fuerza total aplicada dentro de un área específica. ( Lea § Presión. )
De la misma manera, la cantidad de temperatura , medible macroscópicamente , es una cuantificación de la cantidad total de movimiento, o energía cinética , que exhiben las partículas. ( Lea § Temperatura. )
En la teoría cinética de los gases , se supone que la energía cinética consiste puramente en traslaciones lineales de acuerdo con una distribución de velocidad de las partículas en el sistema. Sin embargo, en los gases reales y otras sustancias reales, los movimientos que definen la energía cinética de un sistema (que determinan colectivamente la temperatura), son mucho más complejos que la simple traslación lineal debido a la estructura más compleja de las moléculas, en comparación con los átomos individuales que actúan de manera similar a las masas puntuales . En los sistemas termodinámicos reales, los fenómenos cuánticos juegan un papel importante en la determinación de los movimientos térmicos. Los movimientos térmicos aleatorios (energía cinética) en las moléculas son una combinación de un conjunto finito de movimientos posibles que incluyen traslación, rotación y vibración . Este rango finito de movimientos posibles, junto con el conjunto finito de moléculas en el sistema, conduce a un número finito de microestados dentro del sistema; llamamos al conjunto de todos los microestados un conjunto . Específicamente para los sistemas atómicos o moleculares, potencialmente podríamos tener tres tipos diferentes de conjunto, dependiendo de la situación: conjunto microcanónico , conjunto canónico o conjunto gran canónico . Las combinaciones específicas de microestados dentro de un conjunto son la forma en que realmente definimos el macroestado del sistema (temperatura, presión, energía, etc.). Para ello, primero debemos contar todos los microestados mediante el uso de una función de partición . El uso de la mecánica estadística y la función de partición es una herramienta importante en toda la química física, porque es la clave para la conexión entre los estados microscópicos de un sistema y las variables macroscópicas que podemos medir, como la temperatura, la presión, la capacidad calorífica, la energía interna, la entalpía y la entropía, por nombrar solo algunas. ( Lea : Función de partición Significado y significado )
El uso de la función de partición para hallar la energía de una molécula o un sistema de moléculas puede a veces aproximarse mediante el teorema de equipartición , que simplifica enormemente el cálculo. Sin embargo, este método supone que todos los grados de libertad moleculares están igualmente poblados y, por lo tanto, se utilizan igualmente para almacenar energía dentro de la molécula. Esto implicaría que la energía interna cambia linealmente con la temperatura, lo que no es el caso. Esto ignora el hecho de que la capacidad calorífica cambia con la temperatura, debido a que ciertos grados de libertad son inalcanzables (es decir, "se congelan") a temperaturas más bajas. A medida que aumenta la energía interna de las moléculas, también lo hace la capacidad de almacenar energía dentro de grados de libertad adicionales. A medida que se dispone de más grados de libertad para almacenar energía, esto hace que la capacidad calorífica molar de la sustancia aumente. [19]

El movimiento browniano es el modelo matemático que se utiliza para describir el movimiento aleatorio de partículas suspendidas en un fluido. La animación de partículas de gas, que utiliza partículas rosas y verdes, ilustra cómo este comportamiento da lugar a la expansión de los gases ( entropía ). Estos eventos también se describen mediante la teoría de partículas .
Dado que la observación de partículas de gas individuales (átomos o moléculas) está en el límite (o más allá) de la tecnología actual, sólo los cálculos teóricos dan sugerencias sobre cómo se mueven, pero su movimiento es diferente del movimiento browniano porque el movimiento browniano implica un arrastre suave debido a la fuerza de fricción de muchas moléculas de gas, puntuado por violentas colisiones de una (o varias) molécula(s) de gas individuales con la partícula. La partícula (que generalmente consta de millones o miles de millones de átomos) se mueve así en un recorrido irregular, aunque no tan irregular como se esperaría si se examinara una molécula de gas individual.
Las fuerzas entre dos o más moléculas o átomos, ya sean atractivas o repulsivas, se denominan fuerzas intermoleculares . Las moléculas experimentan fuerzas intermoleculares cuando están físicamente próximas entre sí. [20] [21] Estas fuerzas son muy importantes para modelar adecuadamente los sistemas moleculares, así como para predecir con precisión el comportamiento microscópico de las moléculas en cualquier sistema y, por lo tanto, son necesarias para predecir con precisión las propiedades físicas de los gases (y líquidos) en amplias variaciones de las condiciones físicas.
Las fuerzas de van der Waals , una de las fuerzas intermoleculares más importantes de toda la física, surgen del estudio de la química física . Las fuerzas de van der Waals desempeñan un papel clave en la determinación de casi todas las propiedades físicas de los fluidos, como la viscosidad , el caudal y la dinámica de los gases (véase la sección de características físicas). Las interacciones de van der Waals entre las moléculas de los gases son la razón por la que modelar un "gas real" es más difícil matemáticamente que un " gas ideal ". Ignorar estas fuerzas dependientes de la proximidad permite tratar un gas real como un gas ideal , lo que simplifica enormemente el cálculo.
Las atracciones y repulsiones intermoleculares entre dos moléculas de gas dependen de la distancia entre ellas. Las atracciones y repulsiones combinadas están bien modeladas por el potencial de Lennard-Jones , [22] [23] que es uno de los potenciales interatómicos más ampliamente estudiados que describen la energía potencial de los sistemas moleculares. Debido a la aplicabilidad general e importancia, el sistema modelo de Lennard-Jones a menudo se conoce como "Lennard-Jonesio". [24] [25] El potencial de Lennard-Jones entre moléculas se puede dividir en dos componentes separados: una atracción de larga distancia debido a la fuerza de dispersión de London y una repulsión de corto alcance debido a la interacción de intercambio electrón-electrón (que está relacionada con el principio de exclusión de Pauli ).
Cuando dos moléculas están relativamente distantes (es decir, tienen una energía potencial alta ), experimentan una fuerza de atracción débil, lo que hace que se acerquen entre sí, lo que reduce su energía potencial. Sin embargo, si las moléculas están demasiado lejos , no experimentarán una fuerza de atracción significativa. Además, si las moléculas se acercan demasiado , colisionarán y experimentarán una fuerza de repulsión muy alta (modelada por las esferas duras ) que es una fuerza mucho más fuerte que las atracciones, por lo que cualquier atracción debido a la proximidad se descarta.
A medida que dos moléculas se acercan entre sí, desde una distancia que no es ni demasiado lejana ni demasiado cercana, su atracción aumenta a medida que aumenta la magnitud de su energía potencial (volviéndose más negativa) y reduce su energía interna total. [26] La atracción que hace que las moléculas se acerquen, solo puede ocurrir si las moléculas permanecen próximas durante el tiempo que lleva acercarse físicamente . Por lo tanto, las fuerzas de atracción son más fuertes cuando las moléculas se mueven a baja velocidad . Esto significa que la atracción entre moléculas es significativa cuando la temperatura del gas es baja . Sin embargo, si comprimieras isotérmicamente este gas frío en un volumen pequeño, forzando a las moléculas a acercarse y aumentando la presión, las repulsiones comenzarán a dominar sobre las atracciones, ya que la velocidad a la que ocurren las colisiones aumentará significativamente. Por lo tanto, a bajas temperaturas y bajas presiones, la atracción es la interacción intermolecular dominante.
Si dos moléculas se mueven a alta velocidad, en direcciones arbitrarias, a lo largo de trayectorias que no se cruzan, entonces no pasarán suficiente tiempo cerca como para ser afectadas por la fuerza de dispersión de London atractiva. Si las dos moléculas chocan, se están moviendo demasiado rápido y su energía cinética será mucho mayor que cualquier energía potencial atractiva, por lo que solo experimentarán repulsión al chocar. Por lo tanto, las atracciones entre moléculas pueden despreciarse a altas temperaturas debido a las altas velocidades. A altas temperaturas y altas presiones, la repulsión es la interacción intermolecular dominante.
Teniendo en cuenta los efectos antes mencionados que causan estas atracciones y repulsiones, los gases reales se diferencian del modelo de gas ideal por la siguiente generalización: [27]
Una ecuación de estado (para gases) es un modelo matemático que se utiliza para describir o predecir de forma aproximada las propiedades de estado de un gas. En la actualidad, no existe una única ecuación de estado que prediga con precisión las propiedades de todos los gases en todas las condiciones. Por lo tanto, se han desarrollado varias ecuaciones de estado mucho más precisas para gases en rangos específicos de temperatura y presión. Los "modelos de gas" que se discuten más ampliamente son "gas perfecto", "gas ideal" y "gas real". Cada uno de estos modelos tiene su propio conjunto de supuestos para facilitar el análisis de un sistema termodinámico dado. [28] Cada modelo sucesivo amplía el rango de temperatura de cobertura al que se aplica.
La ecuación de estado de un gas ideal o perfecto es la ley de los gases ideales y se lee
donde P es la presión, V es el volumen, n es la cantidad de gas (en unidades molares), R es la constante universal de los gases , 8,314 J/(mol K), y T es la temperatura. Escrita de esta manera, a veces se la denomina la "versión del químico", ya que enfatiza el número de moléculas n . También se puede escribir como
donde es la constante específica de los gases para un gas en particular, en unidades J/(kg K), y ρ = m/V es la densidad. Esta notación es la versión del "dinamista de gases", que resulta más práctica para modelar flujos de gases que implican aceleración sin reacciones químicas.
La ley de los gases ideales no hace suposiciones sobre la capacidad calorífica de un gas. En el caso más general, el calor específico es una función tanto de la temperatura como de la presión. Si se ignora la dependencia de la presión (y posiblemente también la dependencia de la temperatura) en una aplicación particular, a veces se dice que el gas es un gas perfecto , aunque las suposiciones exactas pueden variar según el autor y/o el campo científico.
En el caso de un gas ideal, la ley de los gases ideales se aplica sin restricciones en cuanto al calor específico. Un gas ideal es un "gas real" simplificado, con la suposición de que el factor de compresibilidad Z se establece en 1, lo que significa que esta relación neumática permanece constante. Un factor de compresibilidad de uno también requiere que las cuatro variables de estado sigan la ley de los gases ideales .
Esta aproximación es más adecuada para aplicaciones en ingeniería, aunque se pueden utilizar modelos más simples para producir un rango "aproximado" de dónde debería estar la solución real. Un ejemplo en el que la "aproximación de gas ideal" sería adecuada sería dentro de una cámara de combustión de un motor a reacción . [29] También puede ser útil mantener las reacciones elementales y las disociaciones químicas para calcular las emisiones .

Cada una de las suposiciones que se enumeran a continuación se suma a la complejidad de la solución del problema. A medida que la densidad de un gas aumenta con el aumento de la presión, las fuerzas intermoleculares desempeñan un papel más importante en el comportamiento del gas, lo que hace que la ley de los gases ideales ya no proporcione resultados "razonables". En el extremo superior de los rangos de temperatura del motor (por ejemplo, secciones de la cámara de combustión: 1300 K), las partículas de combustible complejas absorben energía interna por medio de rotaciones y vibraciones que hacen que sus calores específicos varíen de los de las moléculas diatómicas y los gases nobles. A más del doble de esa temperatura, comienza a producirse la excitación electrónica y la disociación de las partículas de gas, lo que hace que la presión se ajuste a un mayor número de partículas (transición de gas a plasma ). [30] Finalmente, se supuso que todos los procesos termodinámicos describían gases uniformes cuyas velocidades variaban de acuerdo con una distribución fija. El uso de una situación de no equilibrio implica que el campo de flujo debe caracterizarse de alguna manera para permitir una solución. Uno de los primeros intentos de ampliar los límites de la ley de los gases ideales fue incluir cobertura para diferentes procesos termodinámicos ajustando la ecuación para leer pV n = constante y luego variando n a través de diferentes valores como la relación de calor específico , γ .
Los efectos reales del gas incluyen aquellos ajustes realizados para tener en cuenta una gama más amplia de comportamiento del gas:
Para la mayoría de las aplicaciones, un análisis tan detallado es excesivo. Ejemplos en los que los efectos reales de los gases tendrían un impacto significativo serían el reingreso al espacio, donde se dieron temperaturas y presiones extremadamente altas, o los gases producidos durante eventos geológicos, como en la imagen de la erupción del Monte Redoubt en 1990 .
El término gas permanente se utiliza para designar un gas cuya temperatura crítica se encuentra por debajo del rango de temperaturas normales de habitabilidad humana y, por lo tanto, no se puede licuar mediante presión dentro de este rango. Históricamente, se creía que estos gases eran imposibles de licuar y, por lo tanto, permanecerían permanentemente en estado gaseoso. El término es relevante para el almacenamiento y transporte de gases a temperatura ambiente y a alta presión. [31]

La ley de Boyle fue quizás la primera expresión de una ecuación de estado. En 1662, Robert Boyle realizó una serie de experimentos empleando un tubo de vidrio en forma de J, que estaba sellado en un extremo. Se agregó mercurio al tubo, atrapando una cantidad fija de aire en el extremo corto y sellado del tubo. Luego, se midió cuidadosamente el volumen de gas a medida que se agregaba mercurio adicional al tubo. La presión del gas podía determinarse por la diferencia entre el nivel de mercurio en el extremo corto del tubo y el del extremo largo y abierto. La imagen del equipo de Boyle muestra algunas de las herramientas exóticas utilizadas por Boyle durante su estudio de los gases.
A través de estos experimentos, Boyle observó que la presión ejercida por un gas mantenido a una temperatura constante varía inversamente con el volumen del gas. [32] Por ejemplo, si el volumen se reduce a la mitad, la presión se duplica; y si el volumen se duplica, la presión se reduce a la mitad. Dada la relación inversa entre presión y volumen, el producto de la presión ( P ) y el volumen ( V ) es una constante ( k ) para una masa dada de gas confinado siempre que la temperatura sea constante. Enunciado como una fórmula, es:
Debido a que los volúmenes y presiones antes y después de la cantidad fija de gas, donde las temperaturas antes y después son las mismas, son iguales a la constante k , se pueden relacionar mediante la ecuación:
En 1787, el físico francés y pionero de los globos aerostáticos, Jacques Charles , descubrió que el oxígeno, el nitrógeno, el hidrógeno, el dióxido de carbono y el aire se expanden en la misma medida en el mismo intervalo de 80 kelvin. Observó que, para un gas ideal a presión constante, el volumen es directamente proporcional a su temperatura:
En 1802, Joseph Louis Gay-Lussac publicó los resultados de experimentos similares, aunque más extensos. [33] Gay-Lussac atribuyó el trabajo anterior de Charles al nombrar la ley en su honor. Al propio Gay-Lussac se le atribuye la ley que describe la presión, que descubrió en 1809. Establece que la presión ejercida sobre los lados de un recipiente por un gas ideal es proporcional a su temperatura.
En 1811, Amedeo Avogadro verificó que volúmenes iguales de gases puros contienen el mismo número de partículas. Su teoría no fue aceptada de forma generalizada hasta 1858, cuando otro químico italiano, Stanislao Cannizzaro, fue capaz de explicar las excepciones no ideales. Por su trabajo con gases un siglo antes, la constante física que lleva su nombre (la constante de Avogadro ) es el número de átomos por mol de carbono-12 elemental (6,022 × 10 23 mol −1 ). Este número específico de partículas de gas, a temperatura y presión estándar (ley de los gases ideales) ocupa 22,40 litros, lo que se denomina volumen molar .
La ley de Avogadro establece que el volumen que ocupa un gas ideal es proporcional a la cantidad de sustancia que hay en él. Esto da lugar al volumen molar de un gas, que en condiciones normales es de 22,4 dm 3 /mol (litros por mol). La relación viene dada por donde n es la cantidad de sustancia del gas (el número de moléculas dividido por la constante de Avogadro ).

En 1801, John Dalton publicó la ley de presiones parciales a partir de su trabajo sobre la relación de la ley de los gases ideales: la presión de una mezcla de gases no reactivos es igual a la suma de las presiones de todos los gases constituyentes por separado. Matemáticamente, esto se puede representar para n especies como:
La imagen del diario de Dalton muestra la simbología que utilizó como abreviatura para registrar el camino que siguió. Entre las observaciones clave que hizo en su diario sobre la mezcla de "fluidos elásticos" no reactivos (gases) se encuentran las siguientes: [34]

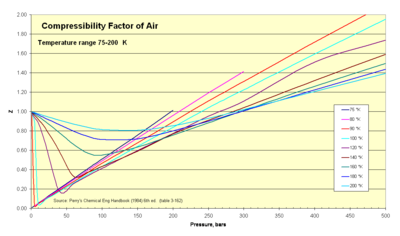
Los termodinámicos utilizan este factor ( Z ) para alterar la ecuación de los gases ideales y tener en cuenta los efectos de compresibilidad de los gases reales. Este factor representa la relación entre los volúmenes específicos reales e ideales. A veces se lo denomina "factor de corrección" para ampliar el rango útil de la ley de los gases ideales con fines de diseño. Por lo general, este valor Z es muy cercano a la unidad. La imagen del factor de compresibilidad ilustra cómo varía Z en un rango de temperaturas muy frías.

Las partículas, en efecto, se "adherirán" a la superficie de un objeto que se mueva a través de ella. Esta capa de partículas se llama capa límite. En la superficie del objeto, es esencialmente estática debido a la fricción de la superficie. El objeto, con su capa límite, es efectivamente la nueva forma del objeto que el resto de las moléculas "ven" a medida que el objeto se acerca. Esta capa límite puede separarse de la superficie, creando esencialmente una nueva superficie y cambiando por completo la trayectoria del flujo. El ejemplo clásico de esto es un perfil aerodinámico en pérdida . La imagen del ala delta muestra claramente el engrosamiento de la capa límite a medida que el gas fluye de derecha a izquierda a lo largo del borde de ataque.

En dinámica de fluidos, la turbulencia o flujo turbulento es un régimen de flujo caracterizado por cambios caóticos y estocásticos en las propiedades. Esto incluye difusión de momento bajo, convección de momento alto y variación rápida de presión y velocidad en el espacio y el tiempo. La vista satelital del clima alrededor de las islas Robinson Crusoe ilustra un ejemplo.
La viscosidad, una propiedad física, es una medida de la adherencia entre moléculas adyacentes. Un sólido puede soportar una fuerza de corte debido a la fuerza de estas fuerzas intermoleculares pegajosas. Un fluido se deformará continuamente cuando se someta a una carga similar. Si bien un gas tiene un valor de viscosidad menor que un líquido, sigue siendo una propiedad observable. Si los gases no tuvieran viscosidad, no se pegarían a la superficie de un ala y no formarían una capa límite. Un estudio del ala delta en la imagen de Schlieren revela que las partículas de gas se adhieren entre sí (consulte la sección Capa límite).
En mecánica de fluidos, el número de Reynolds es la relación entre las fuerzas inerciales ( v s ρ ) que dominan un flujo turbulento y las fuerzas viscosas ( μ/L ) que son proporcionales a la viscosidad. Es uno de los números adimensionales más importantes en dinámica de fluidos y se utiliza, normalmente junto con otros números adimensionales, para proporcionar un criterio para determinar la similitud dinámica. Como tal, el número de Reynolds proporciona el vínculo entre los resultados del modelado (diseño) y las condiciones reales a escala real. También se puede utilizar para caracterizar el flujo.
A medida que el número total de grados de libertad se acerca al infinito, el sistema se encontrará en el macroestado que corresponde a la multiplicidad más alta . Para ilustrar este principio, observe la temperatura superficial de una barra de metal congelada. Utilizando una imagen térmica de la temperatura superficial, observe la distribución de temperatura en la superficie. Esta observación inicial de temperatura representa un " microestado ". En algún momento futuro, una segunda observación de la temperatura superficial produce un segundo microestado. Al continuar este proceso de observación, es posible producir una serie de microestados que ilustran la historia térmica de la superficie de la barra. La caracterización de esta serie histórica de microestados es posible al elegir el macroestado que los clasifica con éxito a todos en una sola agrupación.
Cuando cesa la transferencia de energía de un sistema, esta condición se conoce como equilibrio termodinámico. Por lo general, esta condición implica que el sistema y el entorno están a la misma temperatura, por lo que ya no se transfiere calor entre ellos. También implica que las fuerzas externas están equilibradas (el volumen no cambia) y que todas las reacciones químicas dentro del sistema se han completado. El tiempo que transcurre hasta que se produce este fenómeno varía según el sistema en cuestión. Un recipiente con hielo que se deja derretir a temperatura ambiente tarda horas, mientras que en los semiconductores la transferencia de calor que se produce en la transición del dispositivo de un estado encendido a uno apagado podría ser del orden de unos pocos nanosegundos.
Probablemente no haya fundamento en la idea (que se encuentra desde el siglo XVIII en adelante, por ejemplo, en J. Priestley On Air (1774) Introd. 3) de que van Helmont modeló el gas a partir del espíritu geest holandés, o cualquiera de sus afines.
{{citation}}: Falta o está vacío |title=( ayuda )