entero gaussiano

En teoría de números , un entero gaussiano es un número complejo cuyas partes real e imaginaria son ambas enteras . Los enteros gaussianos, con la suma y multiplicación ordinaria de números complejos , forman un dominio integral , generalmente escrito como o ^[1] $\mathbf {Z} [i]$ $\mathbb {Z} [i].$

Los enteros gaussianos comparten muchas propiedades con los números enteros: forman un dominio euclidiano y, por tanto, tienen una división euclidiana y un algoritmo euclidiano ; esto implica factorización única y muchas propiedades relacionadas. Sin embargo, los enteros gaussianos no tienen un orden total que respete la aritmética.

Los enteros gaussianos son enteros algebraicos y forman el anillo más simple de enteros cuadráticos .

Los enteros gaussianos llevan el nombre del matemático alemán Carl Friedrich Gauss .

Definiciones basicas

Los enteros gaussianos son el conjunto ^[1]

\mathbf {Z} [i]=\{a+bi\mid a,b\in \mathbf {Z} \},\qquad {\text{ donde }}i^{2}=-1.

En otras palabras, un entero gaussiano es un número complejo tal que sus partes real e imaginaria son ambas enteras . Dado que los enteros gaussianos son cerrados en la suma y la multiplicación, forman un anillo conmutativo , que es un subanillo del cuerpo de números complejos. Es por tanto un dominio integral .

Cuando se consideran dentro del plano complejo , los enteros gaussianos constituyen la red de enteros $bidimensional$ .

El conjugado de un entero gaussiano $a + bi$ es el entero gaussiano $a - bi$ .

La norma de un entero gaussiano es su producto por su conjugado.

N(a+bi)=(a+bi)(a-bi)=a^{2}+b^{2}.

La norma de un número entero gaussiano es, por tanto, el cuadrado de su valor absoluto como número complejo. La norma de un entero gaussiano es un entero no negativo, que es la suma de dos cuadrados . $Por tanto ,$ una norma no puede ser de la forma $4k + 3$ , con $k$ entero .

La norma es multiplicativa , es decir, se tiene ^[2]

N(zw)=N(z)N(w),

para cada par de enteros gaussianos $z, w$ . Esto se puede demostrar directamente o utilizando la propiedad multiplicativa del módulo de números complejos.

Las unidades del anillo de los enteros gaussianos (es decir, los enteros gaussianos cuyo inverso multiplicativo también es un entero gaussiano) son precisamente los enteros gaussianos con norma 1, es decir, 1, –1 $,$ $i$ y $-i$ . ^[3]

división euclidiana

Visualización de la distancia máxima a algún entero gaussiano.

Los enteros gaussianos tienen una división euclidiana (división con resto) similar a la de los números enteros y polinomios . Esto convierte a los enteros gaussianos en un dominio euclidiano e implica que los enteros gaussianos comparten con los enteros y los polinomios muchas propiedades importantes, como la existencia de un algoritmo euclidiano para calcular los máximos divisores comunes , la identidad de Bézout , la propiedad ideal principal , el lema de Euclides , la factorización única teorema y el teorema chino del resto , todos los cuales pueden demostrarse utilizando únicamente la división euclidiana.

Un algoritmo de división euclidiana toma, en el anillo de enteros gaussianos, un dividendo $a$ y un divisor $b \neq 0$ , y produce un cociente $q$ y un resto $r$ tal que

a=bq+r\quad {\text{y}}\quad N(r)<N(b).

De hecho, el resto se puede reducir:

a=bq+r\quad {\text{y}}\quad N(r)\leq {\frac {N(b)}{2}}.

Incluso con esta mejor desigualdad, el cociente y el resto no son necesariamente únicos, pero se puede refinar la elección para asegurar la unicidad.

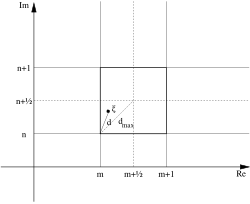
Para probar esto, se puede considerar el cociente de números complejos $x + iy =.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}a/b$ . Hay enteros únicos $m$ y $n$ tales que $- 1 / 2 < x - m\leq 1 / 2$ y $- 1 / 2 < y - n \leq 1 / 2$ , y por tanto $N (x - m + i (y - n)) \leq 1 / 2$ . Tomando $q = m + in$ , se tiene

a=bq+r,

con

r=b{\bigl (}x-m+i(yn){\bigr )},

N(r)\leq {\frac {N(b)}{2}}.

La elección de $x - my$ y $- n$ en un intervalo semiabierto es necesaria para la unicidad $.$ Esta definición de división euclidiana se puede interpretar geométricamente en el plano complejo (ver la figura), observando que la distancia desde un número complejo $ξ$ al entero gaussiano más cercano es como máximo $\sqrt 2 / 2$ . ^[4]

Ideales principales

Dado que el anillo $G$ de los enteros gaussianos es un dominio euclidiano, $G$ es un dominio ideal principal , lo que significa que todo ideal de $G$ es principal . Explícitamente, un ideal $I$ es un subconjunto de un anillo $R$ tal que cada suma de elementos de $I$ y cada producto de un elemento de I $por$ un elemento de $R$ pertenecen a $I.$ Un ideal es principal si consta de todos los múltiplos de un solo elemento $g$ , es decir, tiene la forma

\{gx\mid x\in G\}.

En este caso, se dice que el ideal es generado por $g$ o que $g$ es un generador del ideal.

Todo ideal $I$ en el anillo de los enteros gaussianos es principal, porque, si se elige en $I$ un elemento $g$ distinto de cero de norma mínima, para cada elemento $x$ de $I$ , el resto de la división euclidiana de $x$ por $g$ pertenece también a $I$ y tiene una norma que es menor que la de $g$ ; debido a la elección de $g$ , esta norma es cero y, por tanto, el resto también es cero. Es decir, se tiene $x = qg$ , donde $q$ es el cociente.

Para cualquier $g$ , el ideal generado por $g$ también lo genera cualquier asociado de $g$ , es decir, $g, gi, -g, -gi$ ; ningún otro elemento genera el mismo ideal. Como todos los generadores de un ideal tienen la misma norma, la norma de un ideal es la norma de cualquiera de sus generadores.

En algunas circunstancias, resulta útil elegir, de una vez por todas, un generador para cada ideal. Hay dos formas clásicas de hacerlo, y ambas consideran primero los ideales de norma impar. Si $g = a + bi$ tiene una norma impar $a 2 + b 2$ , entonces uno de $a$ y $b$ es impar y el otro es par. Por tanto, $g$ tiene exactamente un asociado con una parte real $a$ que es impar y positiva. En su artículo original, Gauss hizo otra elección, eligiendo el único asociado tal que el resto de su división por $2 + 2 i$ sea uno. De hecho, como $N (2 + 2 i) = 8$ , la norma del resto no es mayor que 4. Como esta norma es impar y 3 no es la norma de un entero gaussiano, la norma del resto es uno, es decir, el resto es una unidad. Multiplicando $g$ por el inverso de esta unidad, se encuentra un asociado que tiene uno como resto, cuando se divide por $2 + 2 i$ .

Si la norma de $g$ es par, entonces $g = 2 k h$ o $g = 2 k h (1 + i)$ , donde $k$ es un entero positivo y $N (h)$ es impar. Por tanto, se elige el asociado de $g$ para obtener una $h$ que se ajuste a la elección de los asociados para elementos de norma impar.

primos gaussianos

Como los enteros gaussianos forman un dominio ideal principal, también forman un dominio de factorización único . Esto implica que un entero gaussiano es irreducible (es decir, no es producto de dos no unidades ) si y sólo si es primo (es decir, genera un ideal primo ).

Los elementos primos de $Z [i]$ también se conocen como primos gaussianos . Un asociado de un primo gaussiano también es un primo gaussiano. El conjugado de un primo gaussiano también es un primo gaussiano (esto implica que los primos gaussianos son simétricos con respecto a los ejes real e imaginario).

Un número entero positivo es un primo gaussiano si y sólo si es un número primo que es congruente con 3 módulo 4 (es decir, puede escribirse $4 n + 3$ , con $n$ un entero no negativo) (secuencia A002145 en la OEIS ). Los otros números primos no son primos gaussianos, pero cada uno es el producto de dos primos gaussianos conjugados.

Un entero gaussiano $a + bi$ es un primo gaussiano si y sólo si:

uno de $a, b$ es cero y el valor absoluto del otro es un número primo de la forma $4 n + 3$ (siendo $n$ un entero no negativo), o
ambos son distintos de cero y $a 2 + b 2$ es un número primo (que no tendrá la forma $4 n + 3$ ).

En otras palabras, un entero gaussiano es un primo gaussiano si y sólo si su norma es un número primo o es el producto de una unidad ( $\pm1, \pm i$ ) y un número primo de la forma $4 n + 3$ .

De ello se deduce que existen tres casos para la factorización de un número primo $p$ en los enteros gaussianos:

Si $p$ es congruente con 3 módulo 4, entonces es un primo gaussiano; En el lenguaje de la teoría algebraica de números , se dice que $p$ es inerte en los enteros gaussianos.
Si $p$ es congruente con 1 módulo 4, entonces es el producto de un primo gaussiano por su conjugado, los cuales son primos gaussianos no asociados (ninguno es producto del otro por una unidad); $Se dice que p$ es un número primo descompuesto en los números enteros gaussianos. Por ejemplo, $5 = (2 + i)(2 - i)$ y $13 = (3 + 2 i)(3 - 2 i)$ .
Si $p = 2$ , tenemos $2 = (1 + i)(1 - i) = i (1 - i) 2$ ; es decir, 2 es el producto del cuadrado de un primo gaussiano por una unidad; es el único primo ramificado en los enteros gaussianos.

Factorización única

Como para cada dominio de factorización único , cada entero gaussiano puede factorizarse como producto de una unidad y primos gaussianos, y esta factorización es única hasta el orden de los factores, y la sustitución de cualquier primo por cualquiera de sus asociados (incluidos un cambio correspondiente del factor unitario).

Si se elige, de una vez por todas, un primo gaussiano fijo para cada clase de equivalencia de primos asociados, y si se toman sólo estos primos seleccionados en la factorización, entonces se obtiene una factorización prima que es única hasta el orden de los factores. Con las opciones descritas anteriormente, la factorización única resultante tiene la forma

u(1+i)^{e_{0}}{p_{1}}^{e_{1}}\cdots {p_{k}}^{e_{k}},

donde $u$ es una unidad (es decir, $u \in {1, -1, i, - i}$ ), $e 0$ y $k$ son enteros no negativos, $e 1, \dots, e k$ son enteros positivos y $p 1, \dots, p k$ son primos gaussianos distintos tales que, dependiendo de la elección de los asociados seleccionados,

ya sea $p k = a k + ib k$ con $a$ impar y positivo, y $b$ par,
o el resto de la división euclidiana de $p k$ por $2 + 2 i$ es igual a 1 (ésta es la elección original de Gauss ^[5] ).

Una ventaja de la segunda opción es que los asociados seleccionados se comportan bien bajo productos para enteros gaussianos de norma impar. Por otro lado, los asociados seleccionados para los primos gaussianos reales son números enteros negativos. Por ejemplo, la factorización de 231 en los números enteros, y con la primera elección de asociados es 3 × 7 × 11 , mientras que es (–1) × (–3) × (–7) × (–11) con la segunda elección.

racionales gaussianos

El campo de los racionales gaussianos es el campo de las fracciones del anillo de los enteros gaussianos. Está formado por los números complejos cuya parte real e imaginaria son ambas racionales .

El anillo de los enteros gaussianos es la clausura integral de los números enteros en los racionales gaussianos.

Esto implica que los enteros gaussianos son enteros cuadráticos y que un racional gaussiano es un entero gaussiano, si y sólo si es una solución de una ecuación

x^{2}+cx+d=0,

con $cyd$ números $enteros$ . De hecho $a + bi$ es la solución de la ecuación.

x^{2}-2ax+a^{2}+b^{2},

y esta ecuación tiene coeficientes enteros si y sólo si $a$ y $b$ son ambos números enteros.

Máximo común divisor

Como para cualquier dominio de factorización único , un máximo común divisor (mcd) de dos enteros gaussianos $a, b$ es un entero gaussiano $d$ que es un divisor común de $a$ y $b$ , que tiene todos los divisores comunes de $a$ y $b$ como divisor. Es decir (donde $|$ denota la relación de divisibilidad ),

$re | ayd$ $|$ $ banda$
$c | ayc$ $|$ $ b$ implica $c | d$ .

Por lo tanto, mayor se refiere a la relación de divisibilidad y no a un ordenamiento del anillo (para los números enteros, ambos significados de mayor coinciden).

Más técnicamente, un máximo común divisor de $a$ y $b$ es un generador del ideal generado por $a$ y $b$ (esta caracterización es válida para dominios ideales principales , pero no, en general, para dominios de factorización únicos).

El máximo común divisor de dos enteros gaussianos no es único, sino que se define hasta la multiplicación por una unidad . Es decir, dado un máximo común divisor $d$ de $a$ y $b$ , los máximos divisores comunes $de$ $a$ y $b$ son $d, -d, id$ y $-id$ .

Hay varias formas de calcular el máximo común divisor de dos enteros gaussianos $a$ y $b$ . Cuando se conocen las factorizaciones primas de $a$ y $b$ ,

a=i^{k}\prod _{m}{p_{m}}^{\nu _{m}},\quad b=i^{n}\prod _{m}{p_{ m}}^{\mu _ {m}},

donde los primos $p m$ son pares no asociados, y los exponentes $μ m$ no asociados, un máximo común divisor es

\prod _{m}{p_{m}}^{\lambda _{m}},

con

\lambda _ {m}=\min(\nu _ {m},\mu _ {m}).

Desafortunadamente, excepto en casos simples, la factorización prima es difícil de calcular y el algoritmo euclidiano conduce a un cálculo mucho más fácil (y rápido). Este algoritmo consiste en sustituir la entrada $(a, b)$ por $(b, r)$ , donde $r$ es el resto de la división euclidiana de $a$ por $b$ , y repetir esta operación hasta obtener un resto cero, es decir un par $(d, 0)$ . Este proceso termina porque, en cada paso, la norma del segundo entero gaussiano disminuye. El $d$ resultante es un máximo común divisor, porque (en cada paso) $b$ y $r = a - bq$ tienen los mismos divisores que $a$ y $b$ y, por lo tanto, el mismo máximo común divisor.

Este método de cálculo siempre funciona, pero no es tan simple como para los números enteros porque la división euclidiana es más complicada. Por lo tanto, a menudo se prefiere un tercer método para los cálculos escritos a mano. Consiste en señalar que la norma $N (d)$ del máximo común divisor de $a$ y $b$ es común divisor de $N (a)$ , $N (b)$ y $N (a + b)$ . Cuando el máximo común divisor $D$ de estos tres enteros tiene pocos factores, entonces es fácil probar, para el divisor común, todos los enteros gaussianos con una norma que divide a $D.$

Por ejemplo, si $a = 5 + 3 i$ y $b = 2 - 8 i$ , uno tiene $N (a) = 34$ , $N (b) = 68$ y $N (a + b) = 74$ . Como el máximo común divisor de las tres normas es 2, el máximo común divisor de $a$ y $b$ tiene 1 o 2 como norma. Como es necesario un entero gaussiano de norma 2 asociado a $1 + i$ , y como $1 + i$ divide $a$ y $b$ , entonces el máximo común divisor es $1 + i$ .

Si $b$ se reemplaza por su conjugado $b = 2 + 8 i$ , entonces el máximo común divisor de las tres normas es 34, la norma de $a$ , por lo que se puede suponer que el máximo común divisor es $a$ , es decir, que $a | b$ . De hecho, uno tiene $2 + 8 i = (5 + 3 i)(1 + i)$ .

Congruencias y clases de residuos.

Dado un entero gaussiano $z 0$ , llamado módulo , dos enteros gaussianos $z 1, z 2$ son congruentes módulo $z 0$ , si su diferencia es múltiplo de $z 0$ , es decir, si existe un entero gaussiano $q$ tal que $z 1 - z 2 = qz 0$ . En otras palabras, dos enteros gaussianos son congruentes módulo $z 0$ , si su diferencia pertenece al ideal generado por $z 0$ . Esto se denota como $z 1 \equiv z 2 (mod z 0)$ .

El módulo de congruencia $z 0$ es una relación de equivalencia (también llamada relación de congruencia ), que define una partición de los enteros gaussianos en clases de equivalencia , llamadas aquí clases de congruencia o clases de residuos . El conjunto de clases de residuos generalmente se denota $Z [i]/ z 0 Z [i]$ , o $Z [i]/ ⟨ z 0 ⟩$ , o simplemente $Z [i]/ z 0$ .

La clase de residuo de un entero gaussiano $a$ es el conjunto

{\bar {a}}:=\left\{z\in \mathbf {Z} [i]\mid z\equiv a{\pmod {z_{0}}}\right\}

de todos los enteros gaussianos que son congruentes con $a$ . Se deduce que $a = b$ si y sólo si $a \equiv b (mod z 0)$ .

La suma y la multiplicación son compatibles con las congruencias. Esto significa que $a 1 \equiv b 1 (mod z 0)$ y $a 2 \equiv b 2 (mod z 0)$ implican $a 1 + a 2 \equiv b 1 + b 2 (mod z 0)$ y $a 1 a 2 \equiv b 1 b 2 (mod z 0)$ . Esto define operaciones bien definidas (que son independientes de la elección de representantes) sobre las clases de residuos:

{\bar {a}}+{\bar {b}}:={\overline {a+b}}\quad {\text{y}}\quad {\bar {a}}\cdot { \bar {b}}:={\overline {ab}}.

Con estas operaciones, las clases de residuos forman un anillo conmutativo , el anillo cociente de los enteros gaussianos por el ideal generado por $z 0$ , que también se denomina tradicionalmente anillo de clases de residuos módulo $z 0$ (para más detalles, véase Anillo de cociente ).

Ejemplos

Hay exactamente dos clases de residuos para el módulo $1 + i$ , a saber, $0 = {0, \pm2, \pm4,\dots,\pm1 \pm i, \pm3 \pm i,\dots}$ (todos los múltiplos de $1 + i$ ), y $1 = {\pm1, \pm3, \pm5,\dots, \pm i, \pm2 \pm i,\dots}$ , que forman un patrón de tablero de ajedrez en el plano complejo. Estas dos clases forman así un anillo con dos elementos, que es, de hecho, un campo , el único (hasta un isomorfismo) campo con dos elementos, y por tanto puede identificarse con los números enteros módulo 2 . Estas dos clases pueden considerarse como una generalización de la partición de números enteros en enteros pares e impares. Por lo tanto, se puede hablar de enteros gaussianos pares e impares (Gauss dividió además los enteros gaussianos pares en pares , es decir, divisibles por 2, y medio pares ).
Para el módulo 2 hay cuatro clases de residuos, a saber $, 0, 1, i, 1 + i$ . Estos forman un anillo con cuatro elementos, en el que $x = - x$ para cada $x$ . Por tanto, este anillo no es isomorfo con el anillo de números enteros módulo 4, otro anillo con cuatro elementos. Se tiene $1 + i 2 = 0$ y, por tanto, este anillo no es el campo finito con cuatro elementos, ni el producto directo de dos copias del anillo de números enteros módulo 2.
Para el módulo $2 + 2i = (i - 1) 3$ hay ocho clases de residuos, a saber, $0, \pm1, \pm i, 1 \pm i, 2$ , de las cuales cuatro contienen sólo enteros gaussianos pares y cuatro contienen sólo enteros gaussianos impares.

Describir clases de residuos

Las 13 clases de residuos con sus residuos mínimos (puntos azules) en el cuadrado $Q 00$ (fondo verde claro) para el módulo $z 0 = 3 + 2 i$ . Una clase de residuo con $z = 2 - 4 i \equiv - i (mod z 0)$ está resaltada con puntos amarillos/naranjas.

Dado un módulo $z 0$ , todos los elementos de una clase de residuo tienen el mismo resto para la división euclidiana por $z 0$ , siempre que se utilice la división con cociente y resto únicos, que se describe anteriormente. Por tanto, enumerar las clases de residuos equivale a enumerar los posibles restos. Esto se puede hacer geométricamente de la siguiente manera.

En el plano complejo , se puede considerar una cuadrícula , cuyos cuadrados están delimitados por las dos líneas

{\begin{aligned}V_{s}&=\left\{\left.z_{0}\left(s-{\tfrac {1}{2}}+ix\right)\right\vert x\in \mathbf {R} \right\}\quad {\text{and}}\\H_{t}&=\left\{\left.z_{0}\left(x+i\left(t-{\tfrac {1}{2}}\right)\right)\right\vert x\in \mathbf {R} \right\},\end{aligned}}

con números enteros $s$ y $t$ (líneas azules en la figura). Estos dividen el plano en cuadrados semiabiertos (donde $m$ y $n$ son números enteros)

Q_{mn}=\left\{(s+it)z_{0}\left\vert s\in \left[m-{\tfrac {1}{2}},m+{\tfrac {1}{2}}\right),t\in \left[n-{\tfrac {1}{2}},n+{\tfrac {1}{2}}\right)\right.\right\}.

Los intervalos semiabiertos que aparecen en la definición de $Q mn$ han sido elegidos para que cada número complejo pertenezca exactamente a un cuadrado; es decir, los cuadrados $Qmn$ $forman$ una partición del plano complejo. Uno tiene

Q_{mn}=(m+in)z_{0}+Q_{00}=\left\{(m+in)z_{0}+z\mid z\in Q_{00}\right\}.

Esto implica que cada entero gaussiano es congruente módulo $z 0$ con un entero gaussiano único en $Q 00$ (el cuadrado verde en la figura), que es el resto de la división por $z 0$ . En otras palabras, cada clase de residuo contiene exactamente un elemento en $Q 00$ .

Los enteros gaussianos en $Q 00$ (o en su límite ) a veces se denominan residuos mínimos porque su norma no es mayor que la norma de cualquier otro entero gaussiano en la misma clase de residuos (Gauss los llamó residuos absolutamente más pequeños ).

De esto se puede deducir, por consideraciones geométricas, que el número de clases de residuos módulo un entero gaussiano $z 0 = a + bi$ es igual a su norma $N (z 0) = a 2 + b 2$ (ver más abajo una prueba; de manera similar, para números enteros , el número de clases de residuos módulo $n$ es su valor absoluto $| n |$ ).

Prueba

La relación $Q mn = (m + in) z 0 + Q 00$ significa que todos $los Q mn$ se obtienen a partir de $Q 00$ traduciéndolo por un entero gaussiano. Esto implica que todos $los Q mn$ tienen la misma área $N = N (z 0)$ y contienen el mismo número $n g$ de enteros gaussianos.

Generalmente, el número de puntos de la cuadrícula (aquí los enteros gaussianos) en un cuadrado arbitrario con el área $A$ es $A + Θ (\sqrt A)$ (consulte Theta grande para conocer la notación). Si se considera un cuadrado grande que consta de $k \times k$ cuadrados $Q mn$ , entonces contiene $k 2 N + O (k \sqrt N)$ puntos de la cuadrícula. Se sigue $k 2 n g = k 2 N + Θ (k \sqrt N)$ , y por tanto $n g = N + Θ (\sqrt norte / k)$ , después de una división por $k 2$ . Tomando el límite cuando $k$ tiende al infinito se obtiene $n g = N = N (z 0)$ .

Campos de clase de residuo

El módulo de anillo de clase de residuo de un entero gaussiano $z 0$ es un campo si y sólo si es un primo gaussiano. $z_{0}$

Si $z 0$ es un número primo descompuesto o el primo ramificado $1 + i$ (es decir, si su norma $N (z 0)$ es un número primo, que es 2 o un primo congruente con 1 módulo 4), entonces el campo de clase de residuo tiene un número primo de elementos (es decir, $N (z 0)$ ). Por tanto, es isomorfo al campo de los números enteros módulo $N (z 0)$ .

Si, por otro lado, $z 0$ es un primo inerte (es decir, $N (z 0) = p 2$ es el cuadrado de un número primo, que es congruente con 3 módulo 4), entonces el campo de clase de residuo tiene $p 2$ elementos, y es una extensión de grado 2 (única, hasta un isomorfismo) del campo primo con $p$ elementos (los enteros módulo $p$ ).

Grupo de clases de residuos primitivos y función totiente de Euler.

Muchos teoremas (y sus demostraciones) para módulos de números enteros pueden transferirse directamente a módulos de enteros gaussianos, si se reemplaza el valor absoluto del módulo por la norma. Esto es válido especialmente para el grupo de clases de residuos primitivos (también llamado grupo multiplicativo de números enteros módulo $n$ ) y la función totient de Euler . El grupo de clases de residuos primitivos de un módulo $z$ se define como el subconjunto de sus clases de residuos, que contiene todas las clases de residuos $a$ que son coprimos de $z$ , es decir $(a, z) = 1$ . Obviamente, este sistema construye un grupo multiplicativo . El número de sus elementos se denotará por $ϕ (z)$ (análogamente a la función totiente de Euler $φ (n)$ para números enteros $n$ ).

Para los primos gaussianos se sigue inmediatamente que $ϕ (p) = | pag | 2 - 1$ y para enteros gaussianos compuestos arbitrarios

z=i^{k}\prod _{m}{p_{m}}^{\nu _{m}}

La fórmula del producto de Euler se puede derivar como

\phi (z)=\prod _{m\,(\nu _{m}>0)}{\bigl |}{p_{m}}^{\nu _{m}}{\bigr |}^{2}\left(1-{\frac {1}{|p_{m}|{}^{2}}}\right)=|z|^{2}\prod _{p_{m}|z}\left(1-{\frac {1}{|p_{m}|{}^{2}}}\right)

donde el producto se construye sobre todos los divisores primos $p m$ de $z$ (con $ν m > 0$ ). También el importante teorema de Euler se puede transferir directamente:

Para todo

a

con

(a, z) = 1

, se cumple que

a ϕ (z) \equiv 1 (mod z)

Antecedentes históricos

El anillo de los enteros gaussianos fue introducido por Carl Friedrich Gauss en su segunda monografía sobre la reciprocidad cuártica (1832). ^[6] El teorema de la reciprocidad cuadrática (que logró demostrar por primera vez en 1796) relaciona la solubilidad de la congruencia $x 2 \equiv q (mod p)$ con la de $x 2 \equiv p (mod q)$ . De manera similar, la reciprocidad cúbica relaciona la solubilidad de $x 3 \equiv q (mod p)$ con la de $x 3 \equiv p (mod q)$ , y la reciprocidad bicuadrática (o cuártica) es una relación entre $x 4 \equiv q (mod p)$ y $x 4 \equiv p (mód q)$ . Gauss descubrió que la ley de la reciprocidad bicuadrática y sus suplementos se enuncian y prueban más fácilmente como enunciados sobre "números enteros complejos" (es decir, los enteros gaussianos) que como enunciados sobre números enteros ordinarios (es decir, los enteros).

En una nota a pie de página, señala que los números enteros de Eisenstein son el dominio natural para enunciar y demostrar resultados sobre la reciprocidad cúbica e indica que extensiones similares de los números enteros son los dominios apropiados para estudiar leyes de reciprocidad superiores.

Este artículo no sólo presentó los números enteros gaussianos y demostró que son un dominio de factorización único, sino que también introdujo los términos norma, unidad, primario y asociado, que ahora son estándar en la teoría algebraica de números.

Problemas no resueltos

La distribución de los pequeños primos gaussianos en el plano complejo.

La mayoría de los problemas no resueltos están relacionados con la distribución de los números primos gaussianos en el plano.

El problema del círculo de Gauss no trata con los enteros gaussianos per se, sino que pregunta por el número de puntos de la red dentro de un círculo de un radio dado centrado en el origen. Esto equivale a determinar el número de enteros gaussianos con una norma menor que un valor dado.

También hay conjeturas y problemas sin resolver sobre los primos gaussianos. Dos de ellos son:

Los ejes real e imaginario tienen el conjunto infinito de los primos gaussianos 3, 7, 11, 19,... y sus asociados. ¿Hay otras líneas que tengan infinitos números primos gaussianos? En particular, ¿hay infinitos números primos gaussianos de la forma $1 + ki$ ? ^[7]
¿Es posible caminar hasta el infinito utilizando los números primos gaussianos como trampolines y dando pasos de longitud uniformemente delimitada? Esto se conoce como el problema del foso gaussiano ; Fue planteado en 1962 por Basil Gordon y sigue sin resolverse. ^[8]^[9]

Ver también

Entero algebraico
campo ciclotómico
Entero de Eisenstein
prima de eisenstein
cuaternión de Hurwitz
Pruebas del teorema de Fermat sobre sumas de dos cuadrados
Pruebas de reciprocidad cuadrática
Entero cuadrático
La división de ideales primos en extensiones de Galois describe la estructura de los ideales primos en los enteros gaussianos.
Tabla de factorizaciones de enteros gaussianos

Notas

^ ab Fraleigh (1976, pág.286)
^ Fraleigh (1976, pág.289)
^ Fraleigh (1976, pág.288)
^ Fraleigh (1976, pág.287)
^ Gauss (1831, pág.546)
^ Kleiner (1998)
^ Ribenboim, Capítulo III.4.D Capítulo. 6.II, cap. 6.IV (Conjetura E y F de Hardy y Littlewood)
^ Gethner, Ellen; Carro, Stan ; Mecha, Brian (1998). "Un paseo por los números primos gaussianos". El Mensual Matemático Estadounidense . 105 (4): 327–337. doi :10.2307/2589708. JSTOR 2589708. SEÑOR 1614871. Zbl 0946.11002.
^ Chico, Richard K. (2004). Problemas no resueltos en teoría de números (3ª ed.). Springer-Verlag . págs. 55–57. ISBN 978-0-387-20860-2. Zbl 1058.11001.

Referencias

Gauss, CF (1831), "Theoria residuorum biquadraticorum. Commentatio secunda.", Comm. Soc. Reg. Ciencia. Gotinga , 7 : 89-148; reimpreso en Werke, Georg Olms Verlag, Hildesheim, 1973, págs. 93-148. Una traducción al alemán de este artículo está disponible en línea en ″H. Maser (ed.): Arithmetische Untersuchungen über höhere Arithmetik de Carl Friedrich Gauss. Springer, Berlín 1889, págs. 534″.
Fraleigh, John B. (1976), Un primer curso de álgebra abstracta (2ª ed.), Lectura: Addison-Wesley , ISBN 0-201-01984-1
Kleiner, Israel (1998). "De los números a los anillos: la historia temprana de la teoría de los anillos". Elem. Matemáticas . 53 (1): 18–35. doi : 10.1007/s000170050029 . Zbl 0908.16001.
Ribenboim, Paulo (1996). El nuevo libro de registros de números primos (3ª ed.). Nueva York: Springer. ISBN 0-387-94457-5. Zbl 0856.11001.
Henry G. panadero (1993). "Enteros gaussianos complejos para" gráficos gaussianos "". Avisos de ACM SIGPLAN . 28 (11): 22–27. doi :10.1145/165564.165571. S2CID 8083226.

enlaces externos

Texto del compendio de la OMI sobre extensiones cuadráticas y enteros gaussianos en la resolución de problemas
Keith Conrad, Los enteros gaussianos.