Número de Reynolds

Relación entre las fuerzas inerciales y viscosas que actúan sobre un líquido

La columna de humo de esta llama de vela pasa de laminar a turbulenta.

La transición del flujo laminar (izquierda) al turbulento (derecha) del agua de un grifo se produce a medida que aumenta el número de Reynolds.

Una calle de vórtices alrededor de un cilindro. Esto puede ocurrir alrededor de cilindros y esferas, para cualquier fluido, tamaño de cilindro y velocidad de fluido, siempre que tenga un número de Reynolds entre aproximadamente 40 y 1000. ^[1]

George Stokes introdujo los números de Reynolds.

Osborne Reynolds popularizó el concepto.

En dinámica de fluidos , el número de Reynolds ( Re ) es una cantidad adimensional que ayuda a predecir los patrones de flujo de fluidos en diferentes situaciones midiendo la relación entre las fuerzas inerciales y viscosas . ^[2] Con números de Reynolds bajos, los flujos tienden a estar dominados por el flujo laminar (similar a una lámina) , mientras que con números de Reynolds altos, los flujos tienden a ser turbulentos . La turbulencia resulta de las diferencias en la velocidad y la dirección del fluido, que a veces pueden cruzarse o incluso moverse en contra de la dirección general del flujo ( corrientes de Foucault ). Estas corrientes de Foucault comienzan a agitar el flujo, consumiendo energía en el proceso, lo que para los líquidos aumenta las posibilidades de cavitación .

El número de Reynolds tiene una amplia gama de aplicaciones, que abarcan desde el flujo de líquido en una tubería hasta el paso del aire sobre el ala de un avión. Se utiliza para predecir la transición de flujo laminar a turbulento y se utiliza en la escala de situaciones de flujo similares pero de diferente tamaño, como entre un modelo de avión en un túnel de viento y la versión de tamaño real. Las predicciones del inicio de la turbulencia y la capacidad de calcular los efectos de escala se pueden utilizar para ayudar a predecir el comportamiento de los fluidos a mayor escala, como en el movimiento local o global del aire o el agua, y, por lo tanto, los efectos meteorológicos y climatológicos asociados.

El concepto fue introducido por George Stokes en 1851, ^[3] pero el número de Reynolds fue nombrado por Arnold Sommerfeld en 1908 ^[4] en honor a Osborne Reynolds (1842-1912), quien popularizó su uso en 1883. ^{[5] [6]} (cf. esta lista )

Definición

El número de Reynolds es la relación entre las fuerzas inerciales y las fuerzas viscosas dentro de un fluido que está sujeto a un movimiento interno relativo debido a diferentes velocidades del fluido. Una región donde estas fuerzas cambian de comportamiento se conoce como capa límite , como la superficie límite en el interior de una tubería. Un efecto similar se crea mediante la introducción de una corriente de fluido de alta velocidad en un fluido de baja velocidad, como los gases calientes emitidos por una llama en el aire. Este movimiento relativo genera fricción del fluido, que es un factor en el desarrollo del flujo turbulento. Contrarrestando este efecto está la viscosidad del fluido, que tiende a inhibir la turbulencia. El número de Reynolds cuantifica la importancia relativa de estos dos tipos de fuerzas para condiciones de flujo dadas y es una guía para saber cuándo se producirá un flujo turbulento en una situación particular. ^[7]

Esta capacidad de predecir el inicio de un flujo turbulento es una herramienta de diseño importante para equipos como sistemas de tuberías o alas de aviones, pero el número de Reynolds también se utiliza en el escalado de problemas de dinámica de fluidos y se utiliza para determinar la similitud dinámica entre dos casos diferentes de flujo de fluidos, como entre un modelo de avión y su versión de tamaño real. Este escalado no es lineal y la aplicación de los números de Reynolds a ambas situaciones permite desarrollar factores de escalado.

Con respecto a los regímenes de flujo laminar y turbulento :

• El flujo laminar ocurre en números de Reynolds bajos, donde las fuerzas viscosas son dominantes, y se caracteriza por un movimiento de fluido suave y constante;
• El flujo turbulento ocurre en números de Reynolds altos y está dominado por fuerzas inerciales, que tienden a producir remolinos caóticos , vórtices y otras inestabilidades de flujo. ^[8]

El número de Reynolds se define como: ^[4]

${\displaystyle \mathrm {Re} ={\frac {uL}{\nu }}={\frac {\rho uL}{\mu }}}$

dónde:

• ρ es la densidad del fluido ( unidades SI : kg/ ^m3 )
• u es la velocidad del flujo (m/s)
• L es una longitud característica (m)
• μ es la viscosidad dinámica del fluido (Pa·s o N·s/m ² o kg/(m·s))
• ν es la viscosidad cinemática del fluido (m ² /s).

La ecuación de Brezina

El número de Reynolds se puede definir para varias situaciones diferentes en las que un fluido está en movimiento relativo a una superficie. ^{[n 1]} Estas definiciones generalmente incluyen las propiedades del fluido de densidad y viscosidad, más una velocidad y una longitud característica o dimensión característica (L en la ecuación anterior). Esta dimensión es una cuestión de convención; por ejemplo, el radio y el diámetro son igualmente válidos para describir esferas o círculos, pero uno se elige por convención. Para aviones o barcos, se puede utilizar la longitud o el ancho. Para el flujo en una tubería, o para una esfera que se mueve en un fluido, hoy en día se utiliza generalmente el diámetro interno. Otras formas, como tuberías rectangulares u objetos no esféricos, tienen un diámetro equivalente definido. Para fluidos de densidad variable, como gases compresibles o fluidos de viscosidad variable, como fluidos no newtonianos , se aplican reglas especiales. La velocidad también puede ser una cuestión de convención en algunas circunstancias, en particular en recipientes agitados.

En la práctica, la coincidencia del número de Reynolds no es suficiente por sí sola para garantizar la similitud. El flujo de fluidos es generalmente caótico y cambios muy pequeños en la forma y la rugosidad de las superficies limítrofes pueden dar lugar a flujos muy diferentes. No obstante, los números de Reynolds son una guía muy importante y se utilizan ampliamente.

Derivación

Si sabemos que las cantidades físicas relevantes en un sistema físico son sólo , entonces el número de Reynolds está esencialmente fijado por el teorema π de Buckingham . ${\displaystyle \rho ,u,L,\mu }$

En detalle, dado que hay 4 cantidades , pero tienen solo 3 dimensiones (longitud, tiempo, masa), podemos considerar , donde son números reales. Fijando las tres dimensiones de a cero, obtenemos 3 restricciones lineales independientes, por lo que el espacio de solución tiene 1 dimensión y está abarcado por el vector . ${\displaystyle \rho ,u,L,\mu }$ ${\displaystyle \rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}}$ ${\displaystyle x_{1},...,x_{4}}$ ${\displaystyle \rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}}$ ${\displaystyle (1,1,1,-1)}$

Por lo tanto, cualquier cantidad adimensional construida a partir de es una función de , el número de Reynolds. ${\displaystyle \rho ,u,L,\mu }$ ${\displaystyle \rho uL\mu ^{-1}}$

Como alternativa, podemos tomar las ecuaciones incompresibles de Navier-Stokes (forma convectiva) : Si eliminamos el término de gravedad , el lado izquierdo consta de la fuerza inercial y la fuerza viscosa . Su relación tiene el orden de , el número de Reynolds. Este argumento está escrito en detalle en la página del teorema de Scallop . $${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} -\nu \,\nabla ^{2}\mathbf {u} =-{\frac {1}{\rho }}\nabla p+\mathbf {g} }$$ ${\displaystyle {\mathbf {g}}}$ ${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} }$ ${\displaystyle \nu \,\nabla ^{2}\mathbf {u} }$ ${\displaystyle {\frac {(\mathbf {u} \cdot \nabla )\mathbf {u} }{\nu \,\nabla ^{2}\mathbf {u} }}\sim {\frac {u^{2}/L}{\nu u/L^{2}}}={\frac {uL}{\nu }}}$

Derivación alternativa

El número de Reynolds se puede obtener cuando se utiliza la forma adimensional de las ecuaciones incompresibles de Navier-Stokes para un fluido newtoniano expresadas en términos de la derivada lagrangiana :

${\displaystyle \rho {\frac {D\mathbf {v} }{Dt}}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {f} .}$

Cada término de la ecuación anterior tiene las unidades de una "fuerza corporal" (fuerza por unidad de volumen) con las mismas dimensiones de una densidad multiplicada por una aceleración. Por lo tanto, cada término depende de las medidas exactas de un flujo. Cuando se vuelve adimensional la ecuación, es decir, cuando se la multiplica por un factor con unidades inversas de la ecuación base, se obtiene una forma que no depende directamente de los tamaños físicos. Una forma posible de obtener una ecuación adimensional es multiplicar toda la ecuación por el factor

${\displaystyle {\frac {L}{\rho V^{2}}},}$

dónde

• V es la velocidad media, v o v , relativa al fluido (m/s),
• L es la longitud característica (m),
• ρ es la densidad del fluido (kg/m ³ ).

Si ahora establecemos

${\displaystyle {\begin{aligned}\mathbf {v} '&={\frac {\mathbf {v} }{V}},&p'&=p{\frac {1}{\rho V^{2}}},&\mathbf {f} '&=\mathbf {f} {\frac {L}{V^{2}}},&{\frac {\partial }{\partial t'}}&={\frac {L}{V}}{\frac {\partial }{\partial t}},&\nabla '&=L\nabla ,\end{aligned}}}$

Podemos reescribir la ecuación de Navier-Stokes sin dimensiones:

${\displaystyle {\frac {D\mathbf {v} '}{Dt'}}=-\nabla 'p'+{\frac {\mu }{\rho LV}}\nabla '^{2}\mathbf {v} '+\mathbf {f} ',}$

donde el término ⁠micras/ρLV⁠ = ⁠1/Re⁠ .

Finalmente, eliminando los primos para facilitar la lectura:

${\displaystyle {\frac {D\mathbf {v} }{Dt}}=-\nabla p+{\frac {1}{\mathrm {Re} }}\nabla ^{2}\mathbf {v} +\mathbf {f} .}$

Ecuación de sedimentación universal: coeficiente de arrastre, función del número de Reynolds y factor de forma, diagrama 2D

Ecuación de sedimentación universal: coeficiente de arrastre, función del número de Reynolds y factor de forma, diagrama 3D

Por eso, matemáticamente, todos los flujos newtonianos incompresibles con el mismo número de Reynolds son comparables. Observe también que en la ecuación anterior, los términos viscosos se anulan para Re → ∞ . Por lo tanto, los flujos con números de Reynolds altos son aproximadamente no viscosos en la corriente libre.

Historia

Aparato de Osborne Reynolds de 1883 que demuestra el inicio del flujo turbulento. El aparato todavía se encuentra en la Universidad de Manchester.

Diagrama del artículo de Reynolds de 1883 que muestra el inicio del flujo turbulento.

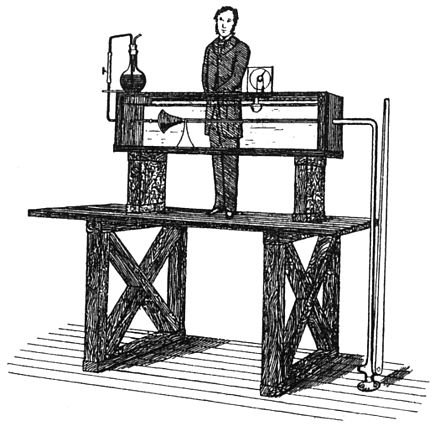
Osborne Reynolds estudió las condiciones en las que el flujo de fluido en tuberías pasaba de flujo laminar a flujo turbulento . En su artículo de 1883, Reynolds describió la transición de flujo laminar a flujo turbulento en un experimento clásico en el que examinó el comportamiento del flujo de agua bajo diferentes velocidades de flujo utilizando una pequeña corriente de agua teñida introducida en el centro de un flujo de agua clara en una tubería más grande.

El tubo más grande era de vidrio, de modo que se podía observar el comportamiento de la capa de la corriente teñida. Al final de este tubo había una válvula de control de flujo que se utilizaba para variar la velocidad del agua dentro del tubo. Cuando la velocidad era baja, la capa teñida se mantenía nítida a lo largo de toda la longitud del tubo grande. Cuando la velocidad aumentaba, la capa se rompía en un punto determinado y se difundía por toda la sección transversal del fluido. El punto en el que esto sucedía era el punto de transición del flujo laminar al turbulento.

De estos experimentos surgió el número de Reynolds adimensional para la similitud dinámica (la relación entre las fuerzas inerciales y las fuerzas viscosas ). Reynolds también propuso lo que ahora se conoce como el promedio de Reynolds de flujos turbulentos, donde las magnitudes como la velocidad se expresan como la suma de los componentes medio y fluctuante. Este promedio permite una descripción "global" del flujo turbulento, por ejemplo, utilizando las ecuaciones de Navier-Stokes promediadas por Reynolds .

Flujo en una tubería

Para el flujo en una tubería o tubo, el número de Reynolds se define generalmente como ^[9]

${\displaystyle \mathrm {Re} ={\frac {uD_{\text{H}}}{\nu }}={\frac {\rho uD_{\text{H}}}{\mu }}={\frac {\rho QD_{\text{H}}}{\mu A}}={\frac {WD_{\text{H}}}{\mu A}},}$

dónde

• D _H es el diámetro hidráulico de la tubería (el diámetro interior si la tubería es circular) (m),
• Q es el caudal volumétrico (m ³ /s),
• A es el área de la sección transversal de la tubería ( A = ⁠πD ²/4⁠ ) ​​(m2 ⁾ ,
• u es la velocidad media del fluido (m/s),
• μ (mu) es la viscosidad dinámica del fluido (Pa·s = N·s/m ² = kg/(m·s)),
• ν (nu) es la viscosidad cinemática ( ν = ⁠micras/ρ⁠ ) ​​(m2 ^/ s),
• ρ (rho) es la densidad del fluido (kg/m ³ ),
• W es el caudal másico del fluido (kg/s).

Para formas tales como conductos cuadrados, rectangulares o anulares donde la altura y el ancho son comparables, la dimensión característica para situaciones de flujo interno se toma como el diámetro hidráulico , D _H , definido como

${\displaystyle D_{\text{H}}={\frac {4A}{P}},}$

donde A es el área de la sección transversal y P es el perímetro mojado . El perímetro mojado de un canal es el perímetro total de todas las paredes del canal que están en contacto con el flujo. ^[10] Esto significa que la longitud del canal expuesta al aire no está incluida en el perímetro mojado.

Para una tubería circular, el diámetro hidráulico es exactamente igual al diámetro interior de la tubería:

${\displaystyle D_{\text{H}}=D.}$

Para un conducto anular, como el canal exterior de un intercambiador de calor de tubo en tubo , el diámetro hidráulico se puede mostrar algebraicamente para reducirse a

${\displaystyle D_{\text{H,annulus}}=D_{\text{o}}-D_{\text{i}},}$

dónde

• D _o es el diámetro interior del tubo exterior,
• D _i es el diámetro exterior del tubo interior.

Para el cálculo que involucra flujo en conductos no circulares, el diámetro hidráulico se puede sustituir por el diámetro de un conducto circular, con una precisión razonable, si la relación de aspecto AR de la sección transversal del conducto permanece en el rango1/4⁠ < AR < 4. ^[11]

Transición laminar-turbulenta

En el flujo de capa límite sobre una placa plana, los experimentos confirman que, después de una cierta longitud de flujo, una capa límite laminar se volverá inestable y turbulenta. Esta inestabilidad ocurre en diferentes escalas y con diferentes fluidos, generalmente cuando Re _x ≈5 × 10 ⁵ , ^[12] donde x es la distancia desde el borde delantero de la placa plana y la velocidad de flujo es la velocidad de corriente libre del fluido fuera de la capa límite.

Para el flujo en una tubería de diámetro D , las observaciones experimentales muestran que para el flujo "plenamente desarrollado", ^{[n 2]} ocurre flujo laminar cuando Re _D < 2300 y flujo turbulento ocurre cuando Re _D > 2900. ^{[13] [14]} En el extremo inferior de este rango, se formará un flujo turbulento continuo, pero solo a una distancia muy larga de la entrada de la tubería. El flujo intermedio comenzará a pasar de laminar a turbulento y luego volverá a laminar a intervalos irregulares, llamado flujo intermitente. Esto se debe a las diferentes velocidades y condiciones del fluido en diferentes áreas de la sección transversal de la tubería, dependiendo de otros factores como la rugosidad de la tubería y la uniformidad del flujo. El flujo laminar tiende a dominar en el centro de movimiento rápido de la tubería, mientras que el flujo turbulento de movimiento más lento domina cerca de la pared. A medida que aumenta el número de Reynolds, el flujo turbulento continuo se acerca a la entrada y la intermitencia entre ellos aumenta, hasta que el flujo se vuelve completamente turbulento en Re _D > 2900. ^[13] Este resultado se generaliza a canales no circulares utilizando el diámetro hidráulico , lo que permite calcular un número de Reynolds de transición para otras formas de canal. ^[13]

Estos números de Reynolds de transición también se denominan números de Reynolds críticos y fueron estudiados por Osborne Reynolds alrededor de 1895. ^[6] El número de Reynolds crítico es diferente para cada geometría. ^[15]

Flujo en un conducto ancho

Para un fluido que se mueve entre dos superficies planas paralelas (donde el ancho es mucho mayor que el espacio entre las placas), la dimensión característica es igual a la distancia entre las placas. ^[16] Esto es consistente con los casos del conducto anular y del conducto rectangular anteriores, llevados a una relación de aspecto límite.

Fluir en un canal abierto

Para calcular el flujo de líquido con una superficie libre, se debe determinar el radio hidráulico . Este es el área de la sección transversal del canal dividida por el perímetro mojado. Para un canal semicircular, es un cuarto del diámetro (en caso de flujo en tubería completa). Para un canal rectangular, el radio hidráulico es el área de la sección transversal dividida por el perímetro mojado. Algunos textos utilizan una dimensión característica que es cuatro veces el radio hidráulico, elegida porque da el mismo valor de Re para el inicio de la turbulencia que en el flujo en tubería, ^[17] mientras que otros utilizan el radio hidráulico como la escala de longitud característica con los consiguientes valores diferentes de Re para el flujo de transición y turbulento.

Flujo alrededor de los perfiles aerodinámicos

Los números de Reynolds se utilizan en el diseño de perfiles aerodinámicos para (entre otras cosas) gestionar el "efecto de escala" al calcular/comparar características (un ala diminuta, escalada para ser enorme, tendrá un rendimiento diferente). ^[18] Los especialistas en dinámica de fluidos definen el número de Reynolds de cuerda R = Vc / ν , donde V es la velocidad de vuelo, c es la longitud de la cuerda y ν es la viscosidad cinemática del fluido en el que opera el perfil aerodinámico, que es1,460 × 10 ⁻⁵  m ² /s para la atmósfera al nivel del mar . ^[19] En algunos estudios especiales se puede utilizar una longitud característica distinta de la cuerda; es raro el "número de Reynolds de envergadura", que no debe confundirse con las estaciones de envergadura en un ala, donde todavía se utiliza la cuerda. ^[20]

Objeto en un fluido

La alta viscosidad de la miel produce un flujo perfectamente laminar cuando se vierte desde un balde, mientras que la baja tensión superficial le permite permanecer en forma de lámina incluso después de alcanzar el fluido que se encuentra debajo. De manera análoga a la turbulencia, cuando el flujo encuentra resistencia, se ralentiza y comienza a oscilar de un lado a otro, acumulándose sobre sí mismo.

_{El número de Reynolds de un} objeto que se mueve en un fluido, llamado número de Reynolds de partícula y a menudo denotado Rep , caracteriza la naturaleza del flujo circundante y su velocidad de caída.

En fluidos viscosos

Flujo arrastrándose junto a una esfera que cae: líneas de corriente , fuerza de arrastre F _d y fuerza de gravedad F _g .

En los casos en que la viscosidad es naturalmente alta, como en el caso de las soluciones de polímeros y los polímeros fundidos, el flujo es normalmente laminar. El número de Reynolds es muy pequeño y la ley de Stokes se puede utilizar para medir la viscosidad del fluido. Se permite que las esferas caigan a través del fluido y alcanzan rápidamente la velocidad terminal , a partir de la cual se puede determinar la viscosidad. ^[21]

El flujo laminar de soluciones de polímeros es aprovechado por animales como peces y delfines, que exudan soluciones viscosas de su piel para facilitar el flujo sobre sus cuerpos mientras nadan. ^[22] Se ha utilizado en carreras de yates por propietarios que quieren obtener una ventaja de velocidad bombeando una solución de polímero como polioxietileno de bajo peso molecular en agua, sobre la superficie mojada del casco.

Sin embargo, esto supone un problema a la hora de mezclar polímeros, ya que se necesita turbulencia para distribuir el relleno fino (por ejemplo) a través del material. Se han desarrollado inventos como el "mezclador de transferencia de cavidades" para producir múltiples pliegues en una masa fundida en movimiento a fin de mejorar la eficiencia de la mezcla . El dispositivo se puede instalar en extrusoras para facilitar la mezcla.

Esfera en un fluido

Coeficiente de arrastre C _d para una esfera en función del número de Reynolds Re , obtenido a partir de experimentos de laboratorio. La línea oscura corresponde a una esfera con una superficie lisa, mientras que la línea más clara corresponde al caso de una superficie rugosa (por ejemplo, con pequeñas hendiduras). Existe un rango de velocidades de fluidos en el que una pelota de golf con una superficie rugosa experimenta menos arrastre que una pelota lisa. Los números a lo largo de la línea indican varios regímenes de flujo y cambios asociados en el coeficiente de arrastre:

2. flujo adherido ( flujo de Stokes ) y flujo separado constante ,
3. flujo inestable separado, que tiene una capa límite de flujo laminar aguas arriba de la separación y que produce una calle de vórtices ,
4. flujo inestable separado con una capa límite laminar en el lado de aguas arriba, antes de la separación del flujo, con aguas abajo de la esfera una estela turbulenta caótica ,
5. flujo separado postcrítico, con una capa límite turbulenta.

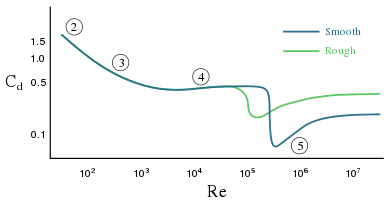
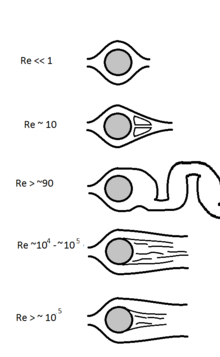
Para una esfera en un fluido, la escala de longitud característica es el diámetro de la esfera y la velocidad característica es la de la esfera en relación con el fluido a cierta distancia de la esfera, de modo que el movimiento de la esfera no perturbe esa parcela de referencia del fluido. La densidad y la viscosidad son las que pertenecen al fluido. ^[23] Nótese que el flujo puramente laminar solo existe hasta Re = 10 según esta definición.

Bajo la condición de baja Re , la relación entre la fuerza y ​​la velocidad del movimiento está dada por la ley de Stokes . ^[24]

En números de Reynolds más altos, la resistencia al avance de una esfera depende de la rugosidad de la superficie. Así, por ejemplo, al añadir hoyuelos a la superficie de una pelota de golf , la capa límite del lado de aguas arriba de la pelota pasa de laminar a turbulenta. La capa límite turbulenta puede permanecer adherida a la superficie de la pelota durante mucho más tiempo que una capa límite laminar y, por lo tanto, crea una estela de baja presión más estrecha y, por lo tanto, una menor resistencia al avance por presión. La reducción de la resistencia al avance por presión hace que la pelota viaje más lejos. ^[25]

Objeto rectangular en un fluido

La ecuación para un objeto rectangular es idéntica a la de una esfera, donde el objeto se aproxima a un elipsoide y el eje de longitud se elige como la escala de longitud característica. Tales consideraciones son importantes en corrientes naturales, por ejemplo, donde hay pocos granos perfectamente esféricos. Para los granos en los que la medición de cada eje es poco práctica, se utilizan en cambio los diámetros de tamiz como la escala de longitud característica de la partícula. Ambas aproximaciones alteran los valores del número crítico de Reynolds.

Velocidad de caída

El número de Reynolds de una partícula es importante para determinar la velocidad de caída de una partícula. Cuando el número de Reynolds de una partícula indica un flujo laminar, se puede utilizar la ley de Stokes para calcular su velocidad de caída o velocidad de sedimentación. Cuando el número de Reynolds de una partícula indica un flujo turbulento, se debe construir una ley de arrastre turbulento para modelar la velocidad de sedimentación adecuada.

Cama llena

Para el flujo de fluido a través de un lecho, de partículas aproximadamente esféricas de diámetro D en contacto, si el vacío es ε y la velocidad superficial es v _s , el número de Reynolds se puede definir como ^[26]

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu }},}$

o

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu \varepsilon }},}$

o

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu (1-\varepsilon )}}.}$

La elección de la ecuación depende del sistema involucrado: la primera es exitosa en correlacionar los datos para varios tipos de lechos empacados y fluidizados , el segundo número de Reynolds es adecuado para los datos de la fase líquida, mientras que la tercera resultó exitosa en correlacionar los datos del lecho fluidizado, siendo introducida por primera vez para el sistema de lecho fluidizado líquido. ^[26]

Las condiciones laminares se aplican hasta Re = 10, y completamente turbulentas a partir de Re = 2000. ^[23]

Recipiente agitado

En un recipiente cilíndrico agitado por una paleta giratoria central, una turbina o una hélice, la dimensión característica es el diámetro del agitador D. La velocidad V es ND , donde N es la velocidad de rotación en rad por segundo. Entonces, el número de Reynolds es:

${\displaystyle \mathrm {Re} ={\frac {\rho ND^{2}}{\mu }}={\frac {\rho VD}{\mu }}.}$

El sistema es completamente turbulento para valores de Re superiores10 000 . ^[27]

Fricción de tuberías

El diagrama de Moody , que describe el factor de fricción de Darcy-Weisbach f como función del número de Reynolds y la rugosidad relativa de la tubería.

Las caídas de presión ^[28] observadas en el flujo completamente desarrollado de fluidos a través de tuberías se pueden predecir utilizando el diagrama de Moody que traza el factor de fricción de Darcy-Weisbach f contra el número de Reynolds Re y la rugosidad relativa .mi/D⁠ . El diagrama muestra claramente los regímenes de flujo laminar, de transición y turbulento a medida que aumenta el número de Reynolds. La naturaleza del flujo en tuberías depende en gran medida de si el flujo es laminar o turbulento.

Similitud de flujos

El comportamiento cualitativo del flujo de fluido sobre un cilindro depende en gran medida del número de Reynolds; a menudo aparecen patrones de flujo similares cuando la forma y el número de Reynolds coinciden, aunque otros parámetros como la rugosidad de la superficie tienen un gran efecto.

Para que dos flujos sean similares, deben tener la misma geometría y los mismos números de Reynolds y Euler . Al comparar el comportamiento de un fluido en puntos correspondientes de un modelo y un flujo a escala real, se cumple lo siguiente:

${\displaystyle {\begin{aligned}\mathrm {Re} _{\text{m}}&=\mathrm {Re} ,\\\mathrm {Eu} _{\text{m}}&=\mathrm {Eu} ,\end{aligned}}}$

donde es el número de Reynolds para el modelo, y es el número de Reynolds a escala completa, y lo mismo ocurre con los números de Euler. ${\displaystyle \mathrm {Re} _{\text{m}}}$ ${\displaystyle \mathrm {Re} }$

Los números de modelo y los números de diseño deben estar en la misma proporción, por lo tanto

${\displaystyle {\frac {p_{\text{m}}}{\rho _{\text{m}}v_{\text{m}}^{2}}}={\frac {p}{\rho v^{2}}}.}$

Esto permite a los ingenieros realizar experimentos con modelos a escala reducida en canales de agua o túneles de viento y correlacionar los datos con los flujos reales, ahorrando en costos durante la experimentación y en tiempo de laboratorio. Tenga en cuenta que la verdadera similitud dinámica también puede requerir la coincidencia de otros números adimensionales , como el número de Mach utilizado en flujos compresibles o el número de Froude que gobierna los flujos en canales abiertos. Algunos flujos involucran más parámetros adimensionales de los que se pueden satisfacer prácticamente con los aparatos y fluidos disponibles, por lo que uno se ve obligado a decidir qué parámetros son los más importantes. Para que el modelado de flujo experimental sea útil, requiere una buena cantidad de experiencia y criterio por parte del ingeniero.

Un ejemplo en el que el mero número de Reynolds no es suficiente para la similitud de los flujos (o incluso el régimen de flujo, laminar o turbulento) son los flujos limitados, es decir, los flujos que están restringidos por paredes u otros límites. Un ejemplo clásico de esto es el flujo de Taylor-Couette , donde la relación adimensional de los radios de los cilindros delimitadores también es importante, y muchas aplicaciones técnicas en las que estas distinciones juegan un papel importante. ^{[29] [30]} Los principios de estas restricciones fueron desarrollados por Maurice Marie Alfred Couette y Geoffrey Ingram Taylor y desarrollados aún más por Floris Takens y David Ruelle .

Valores típicos del número de Reynolds ^{[31] [32]}

• Amebas de Dictyostelium : ~ 1 × 10 ^{−6 [33]}
• Bacteria ~ 1 × 10 ⁻⁴
• Ciliado ~ 1 × 10 ⁻¹
• Pez más pequeño ~ 1
• Flujo sanguíneo en el cerebro ~ 1 × 10 ²
• Flujo sanguíneo en la aorta ~ 1 × 10 ³
• Inicio del flujo turbulento ~ 2,3 × 10 ³ a 5,0 × 10 ⁴ para flujo en tuberías hasta 10 ⁶ para capas límite
• Lanzamiento típico en las Grandes Ligas de Béisbol ~ 2 × 10 ⁵
• Persona nadando ~ 4 × 10 ⁶
• El pez más rápido ~ 1 × 10 ⁸
• Ballena azul ~ 4 × 10 ⁸
• Un gran barco ( Queen Elizabeth 2 ) ~ 5 × 10 ⁹
• Ciclón tropical atmosférico ~ 1 x 10 ¹²

Escalas más pequeñas de movimiento turbulento

En un flujo turbulento, existe un rango de escalas del movimiento del fluido que varía con el tiempo. El tamaño de las escalas más grandes del movimiento del fluido (a veces llamadas remolinos) está determinado por la geometría general del flujo. Por ejemplo, en una chimenea industrial, las escalas más grandes del movimiento del fluido son tan grandes como el diámetro de la chimenea misma. El tamaño de las escalas más pequeñas está determinado por el número de Reynolds. A medida que aumenta el número de Reynolds, se ven escalas cada vez más pequeñas del flujo. En una chimenea, el humo puede parecer tener muchas perturbaciones de velocidad muy pequeñas o remolinos, además de remolinos grandes y voluminosos. En este sentido, el número de Reynolds es un indicador del rango de escalas en el flujo. Cuanto mayor sea el número de Reynolds, mayor será el rango de escalas. Los remolinos más grandes siempre serán del mismo tamaño; los remolinos más pequeños están determinados por el número de Reynolds.

¿Cuál es la explicación de este fenómeno? Un número de Reynolds elevado indica que las fuerzas viscosas no son importantes en grandes escalas del flujo. Con un fuerte predominio de las fuerzas inerciales sobre las viscosas, las mayores escalas de movimiento del fluido no están amortiguadas: no hay suficiente viscosidad para disipar sus movimientos. La energía cinética debe "caer en cascada" desde estas grandes escalas a escalas progresivamente más pequeñas hasta que se alcanza un nivel para el cual la escala es lo suficientemente pequeña como para que la viscosidad se vuelva importante (es decir, las fuerzas viscosas pasan a ser del orden de las inerciales). Es en estas pequeñas escalas donde finalmente tiene lugar la disipación de energía por acción viscosa. El número de Reynolds indica a qué escala se produce esta disipación viscosa. ^[34]

En fisiología

La ley de Poiseuille sobre la circulación sanguínea en el cuerpo depende del flujo laminar . ^[35] En el flujo turbulento, el caudal es proporcional a la raíz cuadrada del gradiente de presión, a diferencia de su proporcionalidad directa al gradiente de presión en el flujo laminar.

Utilizando la definición del número de Reynolds podemos ver que un diámetro grande con flujo rápido, donde la densidad de la sangre es alta, tiende a la turbulencia. Los cambios rápidos en el diámetro de los vasos pueden conducir a un flujo turbulento, por ejemplo, cuando un vaso más estrecho se ensancha hasta convertirse en uno más grande. Además, un abultamiento de ateroma puede ser la causa del flujo turbulento, donde la turbulencia audible puede detectarse con un estetoscopio. ^[36]

Sistemas complejos

La interpretación del número de Reynolds se ha extendido al área de sistemas complejos arbitrarios . Como flujos financieros, ^[37] redes no lineales, ^{[ cita requerida ]} etc. En el último caso, una viscosidad artificial se reduce a un mecanismo no lineal de distribución de energía en medios de red complejos . El número de Reynolds representa entonces un parámetro de control básico que expresa un equilibrio entre los flujos de energía inyectados y disipados para un sistema de límite abierto. Se ha demostrado que el régimen crítico de Reynolds separa dos tipos de movimiento en el espacio de fases: acelerador (atractor) y desacelerador. ^[38] Un número de Reynolds alto conduce a una transición de régimen caótico solo en el marco del modelo de atractor extraño .

Relación con otros parámetros adimensionales

Existen muchos números adimensionales en mecánica de fluidos . El número de Reynolds mide la relación de los efectos de advección y difusión sobre las estructuras en el campo de velocidad y, por lo tanto, está estrechamente relacionado con los números de Péclet , que miden la relación de estos efectos sobre otros campos transportados por el flujo, por ejemplo, la temperatura y los campos magnéticos. Reemplazo de la viscosidad cinemática ν = ⁠micras/ρ⁠ En Re, la difusividad térmica o magnética da como resultado, respectivamente, el número de Péclet térmico y el número de Reynolds magnético . Por lo tanto, estos están relacionados conlos subproductos de Re con proporciones de difusividades, a saber, el número de Prandtl y el número de Prandtl magnético .

Véase también

• Teorema de transporte de Reynolds  : generalización 3D de la regla integral de Leibniz
• Coeficiente de arrastre  : parámetro adimensional para cuantificar la resistencia del fluido
• Deposición (geología)  : proceso geológico en el que se agregan sedimentos, suelo y rocas a una forma de relieve o masa terrestre.
• Inestabilidad de Kelvin-Helmholtz

Referencias

Notas al pie

1. La definición del número de Reynolds no debe confundirse con la ecuación de Reynolds o la ecuación de lubricación.
2. El desarrollo completo del flujo ocurre cuando el flujo ingresa a la tubería, la capa límite se espesa y luego se estabiliza después de varios diámetros de distancia dentro de la tubería.

Citas

1. Tansley y Marshall 2001, págs. 3274–3283.
2. Bush, John WM "Módulo de tensión superficial" (PDF) .
3. Stokes 1851, págs. 8–106.
4. Sommerfeld 1908, págs. 116-124.
5. Reynolds 1883, págs. 935–982.
6. Rott 1990, págs. 1–11.
7. Falkovich 2018.
8. Hall, Nancy (5 de mayo de 2015). «Capa límite». Glenn Research Center . Consultado el 17 de septiembre de 2019 .
9. "Número de Reynolds". Engineeringtoolbox.com . 2003.
10. Holman 2002.
11. Fox, McDonald y Pritchard 2004, pág. 348.
12. Incropera y DeWitt 1981.
13. Schlichting y Gersten 2017, págs.
14. Holman 2002, pág. 207.
15. Potter, Wiggert y Ramadán 2012, p. 105.
16. Seshadri, K (febrero de 1978). "Flujo laminar entre placas paralelas con la inyección de un reactivo con un número de Reynolds elevado". Revista internacional de transferencia de calor y masa . 21 (2): 251–253. Código Bibliográfico :1978IJHMT..21..251S. doi :10.1016/0017-9310(78)90230-2.
17. Callejero 1965.
18. Lissaman 1983, págs. 223–239.
19. "Atmósfera estándar internacional". eng.cam.ac.uk . Consultado el 17 de septiembre de 2019 .
20. Ehrenstein y Eloy 2013, págs. 321–346.
21. "Viscosímetro de bola descendente" (PDF) . Viscosímetro de bola descendente .
22. "No sólo seguir la corriente". American Scientist . 2017-02-06 . Consultado el 2024-05-25 .
23. Rhodes 1989, pág. 29.
24. Dusenbery 2009, pág. 49.
25. "Hoyuelos y resistencia de las pelotas de golf". Aerospaceweb.org . Consultado el 11 de agosto de 2011 .
26. Dwivedi 1977, págs. 157-165.
27. Sinnott, Coulson y Richardson 2005, pág. 73.
28. "Pérdida de carga importante - Pérdida por fricción". Energía nuclear . Consultado el 17 de septiembre de 2019 .
29. "Flujo laminar, transicional y turbulento". rheologic.net . Archivado desde el original el 17 de febrero de 2020 . Consultado el 17 de septiembre de 2019 .
30. Manneville y Pomeau 2009, pág. 2072.
31. Patel, Rodi y Scheuerer 1985, págs. 1308-1319.
32. Dusenbery 2009, pág. 136.
33. Wang, Qixuan; Othmer, Hans G. (1 de junio de 2016). "Análisis computacional de la natación ameboides con un número de Reynolds bajo". Revista de biología matemática . 72 (7): 1893–1926. arXiv : 1509.03504 . doi :10.1007/s00285-015-0925-9. ISSN  1432-1416. PMID  26362281. S2CID  253808496.
34. https://www.cfd-online.com/Wiki/Reynolds_number
35. Ayuda, EPW; McDonald, DA (28 de junio de 1954). "Observaciones sobre el flujo laminar en las venas". Revista de fisiología . 124 (3): 631–639. doi :10.1113/jphysiol.1954.sp005135. PMC 1366298 . PMID  13175205. 
36. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4258672/
37. Los 2006, pág. 369.
38. Gómez Blázquez, Alberto (23 de junio de 2016). Análisis aerodinámico del suelo plano (Tesis de licenciatura). Universitat Politècnica de Catalunya.

Fuentes

• Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2006). Fenómenos de transporte. John Wiley & Sons. ISBN 978-0-470-11539-8.
• Dusenbery, David B. (2009). Vivir a escala micro . Cambridge, Massachusetts: Harvard University Press. ISBN 9780674031166.
• Dwivedi, PN (1977). "Transferencia de masa partícula-fluido en lechos fijos y fluidizados". Diseño y desarrollo de procesos de química industrial e ingeniería . 16 (2): 157–165. doi :10.1021/i260062a001.
• Ehrenstein, Uwe; Eloy, Christophe (2013). "Fricción de la piel en una pared móvil y sus implicaciones para los animales nadadores" (PDF) . Journal of Fluid Mechanics . 718 : 321–346. Bibcode :2013JFM...718..321E. doi :10.1017/jfm.2012.613. ISSN  0022-1120. S2CID  56331294. Archivado desde el original (PDF) el 2 de marzo de 2019.
• Falkovich, Gregory (2018). Mecánica de fluidos. Cambridge University Press. ISBN 978-1-107-12956-6.
• Fox, RW; McDonald, AT; Pritchard, Phillip J. (2004). Introducción a la mecánica de fluidos (6.ª ed.). Hoboken: John Wiley and Sons. pág. 348. ISBN 978-0-471-20231-8.
• Holman, JP (2002). Transferencia de calor (edición en unidades SI). McGraw-Hill Education (India) Pvt Limited. ISBN 978-0-07-106967-0.
• Incropera, Frank P.; DeWitt, David P. (1981). Fundamentos de la transferencia de calor. Nueva York: Wiley. ISBN 978-0-471-42711-7.
• Lissaman, PBS (1983). "Perfiles aerodinámicos de bajo número de Reynolds". Annu. Rev. Fluid Mech . 15 (15): 223–39. Código Bibliográfico :1983AnRFM..15..223L. CiteSeerX  10.1.1.506.1131 . doi :10.1146/annurev.fl.15.010183.001255. S2CID  123639541.
• Los, Cornelis (2006). Riesgo de los mercados financieros: medición y análisis. Routledge. ISBN 978-1-134-46932-1.
• Manneville, Paul; Pomeau, Yves (25 de marzo de 2009). "Transición a la turbulencia". Scholarpedia . 4 (3): 2072. Bibcode :2009SchpJ...4.2072M. doi : 10.4249/scholarpedia.2072 .
• Patel, VC; Rodi, W.; Scheuerer, G. (1985). "Modelos de turbulencia para flujos cercanos a la pared y de bajo número de Reynolds: una revisión". AIAA Journal . 23 (9): 1308–1319. Bibcode :1985AIAAJ..23.1308P. doi :10.2514/3.9086.
• Potter, Merle C.; Wiggert, David C.; Ramadan, Bassem H. (2012). Mecánica de fluidos (4.ª edición, unidades del SI). Cengage Learning. ISBN 978-0-495-66773-5.
• Reynolds, Osborne (1883). "Una investigación experimental de las circunstancias que determinan si el movimiento del agua será directo o sinuoso, y de la ley de resistencia en canales paralelos". Philosophical Transactions of the Royal Society . 174 : 935–982. Bibcode :1883RSPT..174..935R. doi : 10.1098/rstl.1883.0029 . JSTOR  109431.
• Rhodes, M. (1989). Introducción a la tecnología de partículas. Wiley. ISBN 978-0-471-98482-5.
• Rott, N. (1990). "Nota sobre la historia del número de Reynolds" (PDF) . Annual Review of Fluid Mechanics . 22 (1): 1–11. Bibcode :1990AnRFM..22....1R. doi :10.1146/annurev.fl.22.010190.000245. S2CID  54583669. Archivado desde el original (PDF) el 25 de febrero de 2019.
• Schlichting, Hermann; Gersten, Klaus (2017). Teoría de la capa límite. Saltador. ISBN 978-3-662-52919-5.
• Sinnott, RK; Coulson, John Metcalfe; Richardson, John Francis (2005). Diseño de ingeniería química. Vol. 6 (4.ª ed.). Elsevier Butterworth-Heinemann. ISBN 978-0-7506-6538-4.
• Sommerfeld, Arnold (1908). "Ein Beitrag zur hydrodynamischen Erkläerung der turbulenten Flüssigkeitsbewegüngen (Una contribución a la explicación hidrodinámica de los movimientos de fluidos turbulentos)" (PDF) . Congreso Internacional de Matemáticos . 3 : 116-124. Archivado desde el original (PDF) el 15 de noviembre de 2016.
• Stokes, George (1851). "Sobre el efecto de la fricción interna de los fluidos en el movimiento de los péndulos". Transactions of the Cambridge Philosophical Society . 9 : 8–106. Bibcode :1851TCaPS...9....8S.
• Streeter, Victor Lyle (1965). Mecánica de fluidos (3.ª ed.). Nueva York: McGraw-Hill. OCLC  878734937.
• Tansley, Claire E.; Marshall, David P. (2001). "Flujo que pasa por un cilindro en un plano, con aplicación a la separación de la corriente del Golfo y la corriente circumpolar antártica" (PDF) . Journal of Physical Oceanography . 31 (11): 3274–3283. Bibcode :2001JPO....31.3274T. doi :10.1175/1520-0485(2001)031<3274:FPACOA>2.0.CO;2. Archivado desde el original (PDF) el 2011-04-01.

Lectura adicional

1. Batchelor, GK (1967). Introducción a la dinámica de fluidos . Cambridge University Press. págs. 211–215.
2. Brezina, Jiri, 1979, Distribuciones de tamaño de partículas y velocidad de sedimentación de materiales del tamaño de arena: 2º Simposio Europeo sobre Caracterización de Partículas (PARTEC), Núremberg, Alemania Occidental.
3. Brezina, Jiri, 1980, Interpretación sedimentológica de errores en el análisis de tamaño de arenas; 1ª Reunión Europea de la Asociación Internacional de Sedimentólogos, Universidad del Ruhr en Bochum, República Federal de Alemania, marzo de 1980.
4. Brezina, Jiri, 1980, Distribución del tamaño de la arena - interpretación sedimentológica; 26º Congreso Geológico Internacional, París , julio de 1980, Resúmenes, vol. 2.
5. Fouz, Infaz, "Mecánica de fluidos", Departamento de Ingeniería Mecánica, Universidad de Oxford, 2001, pág. 96
6. Hughes, Roger "Civil Engineering Hydraulics", Departamento Civil y Ambiental, Universidad de Melbourne 1997, págs. 107-152
7. Jermy M., "Mecánica de fluidos: un libro de lectura", Departamento de Ingeniería Mecánica, Universidad de Canterbury, 2005, págs. 5 y 10.
8. Purcell, EM "Vida con un número de Reynolds bajo", American Journal of Physics vol 45, págs. 3-11 (1977)[1]
9. Truskey, GA, Yuan, F, Katz, DF (2004). Fenómenos de transporte en sistemas biológicos Prentice Hall, págs. 7. ISBN 0-13-042204-5 . ISBN 978-0-13-042204-0 .  
10. Zagarola, MV y Smits, AJ, "Experimentos en flujo turbulento en tuberías con alto número de Reynolds". Documento AIAA n.° 96-0654, 34.ª Reunión de Ciencias Aeroespaciales de la AIAA, Reno, Nevada, 15 al 18 de enero de 1996.
11. Isobel Clark, 1977, ROKE, un programa informático para la descomposición por mínimos cuadrados no lineal de mezclas de distribuciones; Computer & Geosciences (Pergamon Press), vol. 3, pág. 245 - 256.
12. BC Colby y RP Christensen, 1957, Algunos fundamentos del análisis del tamaño de partículas; St. Anthony Falls Hydraulic Laboratory, Minneapolis, Minnesota, EE. UU., Informe N.º 12/diciembre, 55 páginas.
13. Arthur T. Corey, 1949, Influencia de la forma en la velocidad de caída de los granos de arena; Tesis de maestría, Colorado Agricultural and Mechanical College, Fort Collins, Colorado, EE. UU., diciembre de 102 páginas.
14. Joseph R. Curray, 1961, Rastreo de masas de sedimentos por modos de tamaño de grano; Proc. Internat. Association of Sedimentology, Informe de la 21.ª sesión de Norden, Internat. Geol. Congress, págs. 119-129.
15. Burghard Walter Flemming y Karen Ziegler, 1995, Patrones de distribución del tamaño de grano de alta resolución y tendencias texturales en el entorno de barrera posterior de la isla Spiekeroog (sur del Mar del Norte); Senckenbergiana Maritima, vol. 26, núm. 1+2, pág. 1 - 24.
16. Robert Louis Folk, 1962, De sesgos y arenas; Jour. Sediment. Petrol., vol. 8, n.º 3/septiembre, pág. 105-111
17. FOLK, Robert Louis y William C. WARD, 1957: Barra del río Brazos: un estudio sobre la importancia de los parámetros del tamaño del grano; Jour. Sediment. Petrol., vol. 27, n.º 1/marzo, pág. 3-26
18. George Herdan, ML Smith y WH Hardwick (1960): Estadística de partículas pequeñas. Segunda edición revisada, Butterworths (Londres, Toronto, etc.), 418 págs.
19. Douglas Inman , 1952: Medidas para describir la distribución del tamaño de los sedimentos. Revista Sediment Petrology, vol. 22, n.º 3/septiembre, pág. 125-145
20. Miroslaw Jonasz, 1991: Tamaño, forma, composición y estructura de micropartículas a partir de dispersión de luz; en SYVITSKI, James PM, 1991, Principios, métodos y aplicaciones del análisis del tamaño de partículas; Cambridge Univ. Press, Cambridge , 368 pp., pág. 147.
21. William C. Krumbein , 1934: Distribución de frecuencias de tamaño de sedimentos; Jour. Sediment. Petrol., vol. 4, No. 2/agosto, pág. 65 - 77.
22. Krumbein, William Christian y Francis J. Pettijohn, 1938: Manual de petrografía sedimentaria; Appleton-Century-Crofts, Inc., Nueva York; 549 págs.
23. John S. McNown y Pin-Nam Lin, 1952, Concentración de sedimentos y velocidad de caída; Actas de la 2.ª Conferencia del Medio Oeste sobre Mecánica de Fluidos, Universidad Estatal de Ohio , Columbus, Ohio ; Reimpresiones de la Universidad Estatal de Iowa en Ingeniería, Reimpresión N.º 109/1952, pág. 401-411.
24. McNownn, John S. y J. Malaika, 1950, Efectos de la forma de las partículas en la velocidad de sedimentación a números de Reynolds bajos; American Geophysical Union Transactions, vol. 31, n.º 1/febrero, pág. 74-82.
25. Gerard V. Middleton 1967, Experimentos sobre corrientes de densidad y turbidez, III; Deposición; Revista Canadiense de Ciencias de la Tierra, vol. 4, pág. 475 - 505 (definición de PSI: pág. 483 - 485).
26. Osborne Reynolds , 1883: Una investigación experimental de las circunstancias que determinan si el movimiento del agua será directo o sinuoso, y de la ley de resistencia en canales paralelos. Phil. Trans. Roy. Soc., 174, Papers, vol. 2, p. 935 - 982
27. EF Schultz, RH Wilde y ML Albertson, 1954, Influencia de la forma en la velocidad de caída de partículas sedimentarias; Colorado Agricultural & Mechanical College, Fort Collins, Colorado, MRD Sediment Series, No. 5/julio (CER 54EFS6), 161 páginas.
28. HJ Skidmore, 1948, Desarrollo de una técnica de suspensión estratificada para el análisis de tamaño-frecuencia; Tesis, Departamento de Mecánica e Hidráulica, Universidad Estatal de Iowa, pág. 2 (? páginas).
29. James PM Syvitski, 1991, Principios, métodos y aplicaciones del análisis del tamaño de partículas; Cambridge Univ. Press, Cambridge, 368 págs.

Enlaces externos

• El número de Reynolds - Las conferencias de Feynman sobre física
• El número de Reynolds a los sesenta símbolos
• Minibiografía de Reynolds y fotografía del aparato original en la Universidad de Manchester.
• Cálculo del número de Reynolds