Diagrama de Dynkin

Representación pictórica de la simetría

En el campo matemático de la teoría de Lie , un diagrama de Dynkin , llamado así por Eugene Dynkin , es un tipo de grafo con algunas aristas duplicadas o triplicadas (dibujado como una línea doble o triple). Los diagramas de Dynkin surgen en la clasificación de álgebras de Lie semisimples sobre cuerpos algebraicamente cerrados , en la clasificación de grupos de Weyl y otros grupos de reflexión finitos , y en otros contextos. Varias propiedades del diagrama de Dynkin (como si contiene múltiples aristas o sus simetrías) corresponden a características importantes del álgebra de Lie asociada.

Diagramas de Dynkin finitos

Diagramas de Dynkin afines (extendidos)

El término "diagrama de Dynkin" puede ser ambiguo. En algunos casos, se supone que los diagramas de Dynkin son dirigidos , en cuyo caso corresponden a sistemas de raíces y álgebras de Lie semisimples, mientras que en otros casos se supone que no son dirigidos , en cuyo caso corresponden a grupos de Weyl. En este artículo, "diagrama de Dynkin" significa diagrama de Dynkin dirigido , y los diagramas de Dynkin no dirigidos se denominarán explícitamente así.

Clasificación de las álgebras de Lie semisimples

El interés fundamental de los diagramas de Dynkin es que clasifican álgebras de Lie semisimples sobre cuerpos algebraicamente cerrados . Se clasifican dichas álgebras de Lie a través de su sistema de raíces , que se puede representar mediante un diagrama de Dynkin. A continuación, se clasifican los diagramas de Dynkin según las restricciones que deben satisfacer, como se describe a continuación.

Eliminar la dirección de los bordes del gráfico corresponde a reemplazar un sistema raíz por el grupo de reflexión finito que genera, el llamado grupo de Weyl , y por lo tanto los diagramas de Dynkin no dirigidos clasifican los grupos de Weyl.

Tienen la siguiente correspondencia para las álgebras de Lie asociadas a grupos clásicos sobre los números complejos:

• ${\displaystyle A_{n}}$: , el álgebra de Lie lineal especial . ${\displaystyle {\mathfrak {sl}}_{n+1}}$
• ${\displaystyle B_{n}}$: , el álgebra de Lie ortogonal especial de dimensión impar . ${\displaystyle {\mathfrak {so}}_{2n+1}}$
• ${\displaystyle C_{n}}$: , el álgebra de Lie simpléctica . ${\displaystyle {\mathfrak {sp}}_{2n}}$
• ${\displaystyle D_{n}}$: , el álgebra de Lie ortogonal especial de dimensión par ( ). ${\displaystyle {\mathfrak {so}}_{2n}}$ ${\displaystyle n>1}$

Para los grupos excepcionales, los nombres del álgebra de Lie y del diagrama de Dynkin asociado coinciden.

Clasificaciones relacionadas

Los diagramas de Dynkin pueden interpretarse como una clasificación de muchos objetos distintos y relacionados, y la notación "A _n , B _n , ..." se utiliza para referirse a todas esas interpretaciones, dependiendo del contexto; esta ambigüedad puede ser confusa.

La clasificación central es que un álgebra de Lie simple tiene un sistema de raíces, al cual está asociado un diagrama de Dynkin (orientado); los tres pueden denominarse B _n , por ejemplo.

El diagrama de Dynkin no orientado es una forma de diagrama de Coxeter y corresponde al grupo de Weyl, que es el grupo de reflexión finito asociado al sistema de raíces. Por lo tanto, B _n puede referirse al diagrama no orientado (un tipo especial de diagrama de Coxeter), al grupo de Weyl (un grupo de reflexión concreto) o al grupo de Coxeter abstracto.

Aunque el grupo de Weyl es isomorfo en abstracto al grupo de Coxeter, un isomorfismo específico depende de una elección ordenada de raíces simples. Asimismo, mientras que la notación del diagrama de Dynkin está estandarizada, la notación del diagrama de Coxeter y del grupo es variada y a veces coincide con la notación del diagrama de Dynkin y a veces no. ^{[ cita requerida ]}

Por último, a veces se hace referencia a objetos asociados con la misma notación, aunque esto no siempre se puede hacer con regularidad. Algunos ejemplos son:

• La red de raíces generada por el sistema de raíces, como en la red E 8 . Esto se define naturalmente, pero no de manera unívoca; por ejemplo, A ₂ y G ₂ generan la red hexagonal .
• Un politopo asociado (por ejemplo, el politopo Gosset 4 ₂₁₎ puede denominarse "politopo E ₈ ", ya que sus vértices se derivan del sistema raíz E ₈ y tiene el grupo de Coxeter E ₈ como grupo de simetría.
• Una forma o variedad cuadrática asociada – por ejemplo, la variedad E 8 tiene una forma de intersección dada por la red E ₈ .

Estas últimas notaciones se utilizan principalmente para objetos asociados a diagramas excepcionales; los objetos asociados a los diagramas regulares (A, B, C, D) tienen, en cambio, nombres tradicionales.

El índice ( n ) es igual al número de nodos en el diagrama, el número de raíces simples en una base, la dimensión de la red de raíces y la amplitud del sistema de raíces, el número de generadores del grupo de Coxeter y el rango del álgebra de Lie. Sin embargo, n no es igual a la dimensión del módulo definitorio (una representación fundamental ) del álgebra de Lie: el índice en el diagrama de Dynkin no debe confundirse con el índice en el álgebra de Lie. Por ejemplo, corresponde a que actúa naturalmente en un espacio de 9 dimensiones, pero tiene rango 4 como álgebra de Lie. ${\displaystyle B_{4}}$ ${\displaystyle {\mathfrak {so}}_{2\cdot 4+1}={\mathfrak {so}}_{9},}$

Los diagramas de Dynkin simplemente enlazados, aquellos que no tienen aristas múltiples (A, D, E) clasifican muchos otros objetos matemáticos; consulte la discusión en Clasificación ADE .

Ejemplo: A2

El sistema de raíces ${\displaystyle A_{2}}$

Por ejemplo, el símbolo puede referirse a: ${\displaystyle A_{2}}$

• El diagrama de Dynkin con 2 nodos conectados,, que también puede interpretarse como un diagrama de Coxeter .
• El sistema de raíces con 2 raíces simples en un ángulo (120 grados). ${\displaystyle 2\pi /3}$
• El álgebra de Lie de rango 2. ${\displaystyle {\mathfrak {sl}}_{2+1}={\mathfrak {sl}}_{3}}$
• El grupo de Weyl de simetrías de las raíces (reflexiones en el hiperplano ortogonal a las raíces), isomorfo al grupo simétrico (de orden 6). ${\displaystyle S_{3}}$
• El grupo Coxeter abstracto , presentado por generadores y relaciones, ${\displaystyle \left\langle r_{1},r_{2}\mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1\right\rangle .}$

Construcción a partir de sistemas de raíces

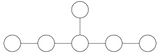
Consideremos un sistema de raíces , asumido como reducido e integral (o "cristalográfico"). En muchas aplicaciones, este sistema de raíces surgirá de un álgebra de Lie semisimple . Sea un conjunto de raíces simples positivas . Luego construimos un diagrama de la siguiente manera. ^[1] Formamos un gráfico con un vértice para cada elemento de . Luego insertamos aristas entre cada par de vértices de acuerdo con la siguiente receta. Si las raíces correspondientes a los dos vértices son ortogonales, no hay arista entre los vértices. Si el ángulo entre las dos raíces es de 120 grados, ponemos una arista entre los vértices. Si el ángulo es de 135 grados, ponemos dos aristas, y si el ángulo es de 150 grados, ponemos tres aristas. (Estos cuatro casos agotan todos los ángulos posibles entre pares de raíces simples positivas. ^[2] ) Finalmente, si hay aristas entre un par de vértices dado, las decoramos con una flecha que apunta desde el vértice correspondiente a la raíz más larga hasta el vértice correspondiente a la más corta. (La flecha se omite si las raíces tienen la misma longitud). Pensar en la flecha como un signo "mayor que" deja claro en qué dirección debe ir la flecha. Los diagramas de Dynkin conducen a una clasificación de los sistemas de raíces. Los ángulos y las razones de longitud entre las raíces están relacionados . ^[3] Por lo tanto, las aristas para raíces no ortogonales pueden describirse alternativamente como una arista para una razón de longitud de 1, dos aristas para una razón de longitud de , y tres aristas para una razón de longitud de . (No hay aristas cuando las raíces son ortogonales, independientemente de la razón de longitud). ${\displaystyle \Delta }$ ${\displaystyle \Delta }$ ${\displaystyle \Delta }$ ${\displaystyle {\sqrt {2}}}$ ${\displaystyle {\sqrt {3}}}$

En el sistema de raíces que se muestra a la derecha, las raíces etiquetadas y forman una base. Como estas dos raíces forman un ángulo de 120 grados (con una relación de longitud de 1), el diagrama de Dynkin consta de dos vértices conectados por una única arista: ${\displaystyle A_{2}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$.

Restricciones

Los diagramas de Dynkin deben satisfacer ciertas restricciones; éstas son esencialmente aquellas satisfechas por los diagramas de Coxeter-Dynkin finitos , junto con una restricción cristalográfica adicional.

Conexión con los diagramas de Coxeter

Los diagramas de Dynkin están estrechamente relacionados con los diagramas de Coxeter de grupos de Coxeter finitos , y la terminología a menudo se confunde. ^{[nota 1]}

Los diagramas de Dynkin se diferencian de los diagramas de Coxeter de grupos finitos en dos aspectos importantes:

Parcialmente dirigida

Los diagramas de Dynkin están parcialmente dirigidos : cualquier borde múltiple (en términos de Coxeter, etiquetado con "4" o más) tiene una dirección (una flecha que apunta de un nodo al otro); por lo tanto, los diagramas de Dynkin tienen más datos que el diagrama de Coxeter subyacente (gráfico no dirigido).

A nivel de sistemas de raíces la dirección corresponde a apuntar hacia el vector más corto; las aristas etiquetadas como "3" no tienen dirección porque los vectores correspondientes deben tener la misma longitud. (Precaución: algunos autores invierten esta convención, con la flecha apuntando hacia el vector más largo.)

Restricción cristalográfica

Los diagramas de Dynkin deben satisfacer una restricción adicional, a saber, que las únicas etiquetas de borde permitidas son 2, 3, 4 y 6, una restricción que no comparten los diagramas de Coxeter, por lo que no todos los diagramas de Coxeter de un grupo finito provienen de un diagrama de Dynkin.

A nivel de sistemas radiculares esto corresponde al teorema de restricción cristalográfica , ya que las raíces forman una red.

Una diferencia adicional, que es sólo estilística, es que los diagramas de Dynkin se dibujan convencionalmente con bordes dobles o triples entre los nodos (para p  = 4, 6), en lugar de un borde etiquetado con " p ".

El término "diagrama de Dynkin" se refiere a veces al grafo dirigido y a veces al grafo no dirigido . Para mayor precisión, en este artículo "diagrama de Dynkin" significará dirigido y el grafo no dirigido subyacente se llamará "diagrama de Dynkin no dirigido". Entonces, los diagramas de Dynkin y los diagramas de Coxeter pueden relacionarse de la siguiente manera:

Con esto se quiere decir que los diagramas de Coxeter de grupos finitos corresponden a grupos puntuales generados por reflexiones, mientras que los diagramas de Dynkin deben satisfacer una restricción adicional correspondiente al teorema de restricción cristalográfica , y que los diagramas de Coxeter no están dirigidos, mientras que los diagramas de Dynkin están (parcialmente) dirigidos.

Los objetos matemáticos correspondientes clasificados por los diagramas son:

El espacio en blanco en la parte superior derecha, correspondiente a los gráficos dirigidos con un gráfico no dirigido subyacente, cualquier diagrama de Coxeter (de un grupo finito), se puede definir formalmente, pero se discute poco y no parece admitir una interpretación simple en términos de objetos matemáticos de interés.

Hay mapas naturales hacia abajo, desde los diagramas de Dynkin a los diagramas de Dynkin no dirigidos; respectivamente, desde los sistemas de raíces a los grupos de Weyl asociados; y hacia la derecha, desde los diagramas de Dynkin no dirigidos a los diagramas de Coxeter; respectivamente, desde los grupos de Weyl a los grupos de Coxeter finitos.

El mapa descendente es sobreyectivo (por definición) pero no biunívoco, ya que los diagramas B _n y C _n se asignan al mismo diagrama no dirigido, por lo que el diagrama de Coxeter y el grupo de Weyl resultantes a veces se denominan BC _n .

El mapa correcto es simplemente una inclusión – los diagramas de Dynkin no dirigidos son casos especiales de diagramas de Coxeter, y los grupos de Weyl son casos especiales de grupos de Coxeter finitos – y no es sobreyectivo, ya que no todo diagrama de Coxeter es un diagrama de Dynkin no dirigido (los diagramas faltantes son H ₃ , H ₄ e I ₂ ( p ) para p  = 5  p  ≥ 7), y correspondientemente no todo grupo de Coxeter finito es un grupo de Weyl.

Isomorfismos

Los isomorfismos excepcionales de los diagramas de Dynkin conexos.

Los diagramas de Dynkin se numeran convencionalmente de modo que la lista no sea redundante: para para para para y comenzando en Sin embargo, las familias se pueden definir para n menores, lo que produce isomorfismos excepcionales de diagramas y correspondientes isomorfismos excepcionales de álgebras de Lie y grupos de Lie asociados. ${\displaystyle n\geq 1}$ ${\displaystyle A_{n},}$ ${\displaystyle n\geq 2}$ ${\displaystyle B_{n},}$ ${\displaystyle n\geq 3}$ ${\displaystyle C_{n},}$ ${\displaystyle n\geq 4}$ ${\displaystyle D_{n},}$ ${\displaystyle E_{n}}$ ${\displaystyle n=6.}$

De manera trivial, se pueden iniciar las familias en o que son todas isomorfas, ya que existe un diagrama vacío único y un diagrama de un nodo único. Los otros isomorfismos de los diagramas de Dynkin conexos son: ${\displaystyle n=0}$ ${\displaystyle n=1,}$

• ${\displaystyle A_{1}\cong B_{1}\cong C_{1}}$
• ${\displaystyle B_{2}\cong C_{2}}$
• ${\displaystyle D_{2}\cong A_{1}\times A_{1}}$
• ${\displaystyle D_{3}\cong A_{3}}$
• ${\displaystyle E_{3}\cong A_{1}\times A_{2}}$
• ${\displaystyle E_{4}\cong A_{4}}$
• ${\displaystyle E_{5}\cong D_{5}}$

Estos isomorfismos corresponden a isomorfismos de álgebras de Lie simples y semisimples, que también corresponden a ciertos isomorfismos de formas de grupos de Lie de estas. También añaden contexto a la familia E n . ^[4]

Automorfismos

El diagrama de Dynkin más simétrico es D ₄ , que da lugar a la trialidad .

Además del isomorfismo entre diferentes diagramas, algunos diagramas también tienen autoisomorfismos o " automorfismos ". Los automorfismos de diagrama corresponden a los automorfismos externos del álgebra de Lie, lo que significa que el grupo de automorfismos externos Out = Aut/Inn es igual al grupo de automorfismos de diagrama. ^{[5] [6] [7]}

Los diagramas que tienen automorfismos no triviales son A _n ( ), D _n ( ), y E ₆ . En todos estos casos excepto para D ₄ , hay un solo automorfismo no trivial (Out = C ₂ , el grupo cíclico de orden 2), mientras que para D ₄ , el grupo de automorfismos es el grupo simétrico en tres letras ( S ₃ , orden 6) – este fenómeno se conoce como " trialidad ". Sucede que todos estos automorfismos de diagramas pueden realizarse como simetrías euclidianas de cómo se dibujan los diagramas convencionalmente en el plano, pero esto es solo un artefacto de cómo se dibujan, y no una estructura intrínseca. ${\displaystyle n>1}$ ${\displaystyle n>1}$

Un ._​

Para A _n , el automorfismo del diagrama invierte el diagrama, que es una línea. Los nodos del diagrama indexan los pesos fundamentales , que (para A _{n −1} ) son para , y el automorfismo del diagrama corresponde a la dualidad. Realizado como el álgebra de Lie, el automorfismo externo se puede expresar como transpuesta negativa, , que es como actúa la representación dual. ^[6] ${\displaystyle \bigwedge ^{i}C^{n}}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle \bigwedge ^{i}C^{n}\mapsto \bigwedge ^{n-i}C^{n}.}$ ${\displaystyle {\mathfrak {sl}}_{n+1},}$ ${\displaystyle T\mapsto -T^{\mathrm {T} }}$

D _n .

Para D _n , el automorfismo del diagrama es cambiar los dos nodos al final de Y, y corresponde a cambiar las dos representaciones de espín quirales . Realizado como el álgebra de Lie, el automorfismo externo se puede expresar como conjugación por una matriz en O(2 n ) con determinante −1. Cuando n = 3, uno tiene por lo que sus automorfismos concuerdan, mientras que está desconectado, y el automorfismo corresponde a cambiar los dos nodos. ${\displaystyle {\mathfrak {so}}_{2n},}$ ${\displaystyle \mathrm {D} _{3}\cong \mathrm {A} _{3},}$ ${\displaystyle \mathrm {D} _{2}\cong \mathrm {A} _{1}\times \mathrm {A} _{1}}$

Para D ₄ , la representación fundamental es isomorfa a las dos representaciones de espín, y el grupo simétrico resultante en tres letras ( S ₃ , o alternativamente el grupo diedro de orden 6, Dih ₃ ) corresponde tanto a los automorfismos del álgebra de Lie como a los automorfismos del diagrama.

Y6 ._​

El grupo de automorfismos de E ₆ corresponde a la inversión del diagrama, y ​​puede expresarse utilizando álgebras de Jordan . ^{[6] [8]}

Los diagramas desconectados, que corresponden a álgebras de Lie semisimples , pueden tener automorfismos derivados del intercambio de componentes del diagrama.

En la característica 2, la flecha en F ₄ se puede ignorar, lo que produce un automorfismo de diagrama adicional y los grupos de Suzuki-Ree correspondientes .

En la característica positiva hay "automorfismos de diagrama" adicionales; en términos generales, en la característica p a veces se permite ignorar la flecha en los enlaces de multiplicidad p en el diagrama de Dynkin cuando se toman automorfismos de diagrama. Así, en la característica 2 hay un automorfismo de orden 2 de y de F ₄ , mientras que en la característica 3 hay un automorfismo de orden 2 de G ₂ . Pero no se aplica en todas las circunstancias: por ejemplo, tales automorfismos no necesariamente surgen como automorfismos del grupo algebraico correspondiente, sino más bien en el nivel de puntos valorados en un cuerpo finito. ${\displaystyle \mathrm {B} _{2}\cong \mathrm {C} _{2}}$

Construcción de grupos de Lie mediante automorfismos de diagramas

Los automorfismos de diagramas a su vez producen grupos de Lie adicionales y grupos de tipo Lie , que son de importancia central en la clasificación de grupos simples finitos.

La construcción del grupo Chevalley de los grupos de Lie en términos de su diagrama de Dynkin no produce algunos de los grupos clásicos, a saber, los grupos unitarios y los grupos ortogonales no divididos . Los grupos de Steinberg construyen los grupos unitarios ² A _n , mientras que los otros grupos ortogonales se construyen como ² D _n , donde en ambos casos esto se refiere a combinar un automorfismo de diagrama con un automorfismo de campo. Esto también produce grupos de Lie exóticos adicionales ² E ₆ y ³ D ₄ , este último solo definido sobre campos con un automorfismo de orden 3.

Los automorfismos adicionales del diagrama en característica positiva producen los grupos de Suzuki-Ree , ² B ₂ , ² F ₄ y ² G ₂ .

Plegable

Plegamientos del grupo Coxeter finitos.

Plegamientos de grupos de Coxeter afines, con tres convenciones de nomenclatura: primero, el conjunto extendido original; el segundo utilizado en el contexto de los gráficos de carcaj ; y el último por Victor Kac para las álgebras de Lie afines retorcidas .

Un diagrama de Dynkin (finito o afín ) (simplemente enlazado) que tiene una simetría (que satisface una condición, a continuación) puede ser cociente por la simetría, produciendo un nuevo diagrama, generalmente de múltiples enlaces, con el proceso llamado plegado (debido a que la mayoría de las simetrías son dobles). A nivel de álgebras de Lie, esto corresponde a tomar la subálgebra invariante bajo el grupo de automorfismos externos, y el proceso puede definirse puramente con referencia a sistemas de raíces, sin usar diagramas. ^[9] Además, cada diagrama de múltiples enlaces (finito o infinito) puede obtenerse plegando un diagrama de simple enlace. ^[10]

La única condición del automorfismo para que el plegado sea posible es que los nodos distintos del grafo en la misma órbita (bajo el automorfismo) no deben estar conectados por una arista; a nivel de sistemas de raíces, las raíces en la misma órbita deben ser ortogonales. ^[10] A nivel de diagramas, esto es necesario ya que de lo contrario el diagrama de cociente tendrá un bucle, debido a que identifica dos nodos pero tiene una arista entre ellos, y los bucles no están permitidos en los diagramas de Dynkin.

Los nodos y aristas del diagrama cociente ("plegado") son las órbitas de los nodos y aristas del diagrama original; las aristas son simples a menos que dos aristas incidentes se mapeen a la misma arista (notablemente en nodos de valencia mayor que 2) – un "punto de ramificación" del mapa, en cuyo caso el peso es el número de aristas incidentes, y la flecha apunta hacia el nodo en el que son incidentes – "el punto de ramificación se mapea al punto no homogéneo". Por ejemplo, en D ₄ plegado a G ₂ , la arista en G ₂ apunta desde la clase de los 3 nodos externos (valencia 1), a la clase del nodo central (valencia 3).

Los plegamientos de los diagramas finitos son: ^{[11] [nota 2]}

• ${\displaystyle A_{2n-1}\to C_{n}}$

(El automorfismo de A _{2 n} no produce un plegamiento porque los dos nodos del medio están conectados por una arista, pero en la misma órbita).

• ${\displaystyle D_{n+1}\to B_{n}}$
• ${\displaystyle D_{4}\to G_{2}}$(si se cociente por el grupo completo o un ciclo de 3, además de de 3 maneras diferentes, si se cociente por una involución) ${\displaystyle D_{4}\to B_{3}}$
• ${\displaystyle E_{6}\to F_{4}}$

Existen plegados similares para diagramas afines, incluidos:

• ${\displaystyle {\tilde {A}}_{2n-1}\to {\tilde {C}}_{n}}$
• ${\displaystyle {\tilde {D}}_{n+1}\to {\tilde {B}}_{n}}$
• ${\displaystyle {\tilde {D}}_{4}\to {\tilde {G}}_{2}}$
• ${\displaystyle {\tilde {E}}_{6}\to {\tilde {F}}_{4}}$

La noción de plegamientos también se puede aplicar de forma más general a los diagramas de Coxeter ^[12] – en particular, se pueden generalizar los cocientes permitidos de los diagramas de Dynkin a H _n e I ₂ ( p ). Geométricamente, esto corresponde a proyecciones de politopos uniformes . En particular, cualquier diagrama de Dynkin simplemente entrelazado se puede plegar a I ₂ ( h ), donde h es el número de Coxeter , que corresponde geométricamente a la proyección al plano de Coxeter .

El plegado se puede aplicar para reducir las preguntas sobre álgebras de Lie (semi-simples) a preguntas sobre álgebras de Lie simplemente enlazadas, junto con un automorfismo, que puede ser más simple que tratar álgebras de múltiples enlaces directamente; esto se puede hacer al construir las álgebras de Lie semi-simples, por ejemplo. Ver Math Overflow: Plegado por automorfismos para más información.

Otros mapas de diagramas

Algunos mapas adicionales de diagramas tienen interpretaciones significativas, como se detalla a continuación. Sin embargo, no todos los mapas de sistemas de raíces surgen como mapas de diagramas. ^[13]

Por ejemplo, hay dos inclusiones de sistemas de raíces de A ₂ en G ₂ , ya sea como las seis raíces largas o las seis raíces cortas. Sin embargo, los nodos en el diagrama G ₂ corresponden a una raíz larga y una raíz corta, mientras que los nodos en el diagrama A ₂ corresponden a raíces de igual longitud y, por lo tanto, este mapa de sistemas de raíces no se puede expresar como un mapa de los diagramas.

Algunas inclusiones de sistemas de raíces pueden expresarse como un diagrama que es un subgrafo inducido de otro, es decir, "un subconjunto de los nodos, con todas las aristas entre ellos". Esto se debe a que eliminar un nodo de un diagrama de Dynkin corresponde a eliminar una raíz simple de un sistema de raíces, lo que produce un sistema de raíces de rango uno inferior. Por el contrario, eliminar una arista (o cambiar la multiplicidad de una arista) mientras se dejan los nodos sin cambios corresponde a cambiar los ángulos entre las raíces, lo que no se puede hacer sin cambiar todo el sistema de raíces. Por lo tanto, se pueden eliminar nodos de manera significativa, pero no aristas. Eliminar un nodo de un diagrama conectado puede producir un diagrama conectado (álgebra de Lie simple), si el nodo es una hoja, o un diagrama desconectado (álgebra de Lie semisimple pero no simple), con dos o tres componentes (este último para D _n y E _n ). A nivel de álgebras de Lie, estas inclusiones corresponden a subálgebras de Lie.

Los subgrafos máximos son los siguientes; los subgrafos relacionados por un automorfismo de diagrama se etiquetan como "conjugados":

• A _{n +1} : A _n , de 2 formas conjugadas.
• B _{n +1} : A _n , B _n .
• C _{n +1} : A _n , C _n .
• D _{n +1} : A _n (2 formas conjugadas), D _n .
• En ₊₁ : _A , _D , _E.​​
  • Para E ₆ , dos de estos coinciden: y son conjugados. ${\displaystyle \mathrm {D} _{5}\cong \mathrm {E} _{5}}$
• F ₄ : Si ₃ , Do ₃ .
• G ₂ : A ₁ , de 2 formas no conjugadas (como raíz larga o raíz corta).

Finalmente, la dualidad de diagramas corresponde a la inversión de la dirección de las flechas, si las hay: ^[13] B _n y C _n son duales, mientras que F ₄ y G ₂ son autoduales, al igual que los diagramas ADE simplemente enlazados.

Simplemente atado

Los diagramas de Dynkin, de estructura simple, clasifican diversos objetos matemáticos; esto se llama clasificación ADE .

Un diagrama de Dynkin sin aristas múltiples se denomina simplemente entrelazado , al igual que el álgebra de Lie y el grupo de Lie correspondientes. Estos son los diagramas, y los fenómenos que estos diagramas clasifican se conocen como clasificación ADE . En este caso, los diagramas de Dynkin coinciden exactamente con los diagramas de Coxeter, ya que no hay aristas múltiples. ${\displaystyle A_{n},D_{n},E_{n}}$

Diagramas de Satake

Los diagramas de Dynkin clasifican las álgebras de Lie semisimples complejas . Las álgebras de Lie semisimples reales se pueden clasificar como formas reales de álgebras de Lie semisimples complejas, y estas se clasifican mediante diagramas de Satake , que se obtienen a partir del diagrama de Dynkin etiquetando algunos vértices en negro (rellenos) y conectando algunos otros vértices en pares mediante flechas, de acuerdo con ciertas reglas.

Historia

Eugenio Dynkin .

Los diagramas de Dynkin reciben su nombre de Eugene Dynkin , quien los utilizó en dos artículos (1946, 1947) que simplificaban la clasificación de las álgebras de Lie semisimples; ^[14] véase (Dynkin 2000). Cuando Dynkin abandonó la Unión Soviética en 1976, lo que en ese momento se consideró equivalente a una traición, se ordenó a los matemáticos soviéticos que hicieran referencia a "diagramas de raíces simples" en lugar de utilizar su nombre. ^{[ cita requerida ]}

Los grafos no dirigidos habían sido utilizados anteriormente por Coxeter (1934) para clasificar grupos de reflexión , donde los nodos correspondían a reflexiones simples; los grafos fueron utilizados luego (con información de longitud) por Witt (1941) en referencia a sistemas de raíces, donde los nodos correspondían a raíces simples, tal como se utilizan hoy. ^{[14] [15]} Dynkin luego los utilizó en 1946 y 1947, reconociendo a Coxeter y Witt en su artículo de 1947.

Convenciones

Los diagramas de Dynkin se han dibujado de varias maneras; ^[15] la convención seguida aquí es común, con ángulos de 180° en los nodos de valencia 2, ángulos de 120° en el nodo de valencia 3 de D _n y ángulos de 90°/90°/180° en el nodo de valencia 3 de E _n , con multiplicidad indicada por 1, 2 o 3 aristas paralelas y longitud de raíz indicada dibujando una flecha en la arista para orientación. Más allá de la simplicidad, un beneficio adicional de esta convención es que los automorfismos de diagramas se realizan mediante isometrías euclidianas de los diagramas.

Las convenciones alternativas incluyen escribir un número por el borde para indicar multiplicidad (comúnmente usado en diagramas de Coxeter), oscurecer los nodos para indicar la longitud de la raíz o usar ángulos de 120° en los nodos de valencia 2 para hacer que los nodos sean más distintos.

También existen convenciones sobre la numeración de los nodos. La convención moderna más común se desarrolló en la década de 1960 y se ilustra en (Bourbaki 1968). ^[15]

Diagramas de Dynkin de rango 2

Los diagramas de Dynkin son equivalentes a matrices de Cartan generalizadas , como se muestra en esta tabla de diagramas de Dynkin de rango 2 con sus correspondientes matrices de Cartan 2  ×  2 .

Para el rango 2, la forma matricial de Cartan es:

${\displaystyle A=\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}$

Un diagrama de múltiples aristas corresponde a los elementos de la matriz de Cartan no diagonales ⁠ ⁠ ${\displaystyle -a_{21},-a_{12}}$ , con el número de aristas dibujadas igual a ⁠ ⁠ ${\displaystyle \max(-a_{21},-a_{12})}$ , y una flecha que apunta hacia los elementos no uno.

Una matriz de Cartan generalizada es una matriz cuadrada tal que: ${\displaystyle A=(a_{ij})}$

1. Para entradas diagonales, . ${\displaystyle a_{ii}=2}$
2. Para entradas no diagonales, . ${\displaystyle a_{ij}\leq 0}$
3. ${\displaystyle a_{ij}=0}$Si y sólo si ${\displaystyle a_{ji}=0}$

La matriz de Cartan determina si el grupo es de tipo finito (si es una matriz definida positiva , es decir, todos los valores propios son positivos), de tipo afín (si no es definida positiva sino semidefinida positiva, es decir, todos los valores propios son no negativos) o de tipo indefinido . El tipo indefinido a menudo se subdivide aún más, por ejemplo, un grupo de Coxeter es lorentziano si tiene un valor propio negativo y todos los demás valores propios son positivos. Además, múltiples fuentes hacen referencia a grupos de Coxeter hiperbólicos , pero hay varias definiciones no equivalentes para este término. En la discusión a continuación, los grupos de Coxeter hiperbólicos son un caso especial de lorentziano, que satisface una condición adicional. Para el rango 2, todas las matrices de Cartan con determinante negativo corresponden al grupo de Coxeter hiperbólico. Pero en general, la mayoría de las matrices con determinante negativo no son ni hiperbólicas ni lorentzianas.

Las ramas finitas tienen , y las ramas afines (con determinante cero) tienen ⁠ ⁠ . ${\displaystyle (-a_{21},-a_{12})=(1,1),(2,1),(3,1)}$ ${\displaystyle (-a_{21},-a_{12})=(2,2){\text{ or }}(4,1)}$

Diagramas de Dynkin finitos

Diagramas de Dynkin afines

Existen extensiones de los diagramas de Dynkin, a saber, los diagramas de Dynkin afines ; estos clasifican las matrices de Cartan de las álgebras de Lie afines . Estos se clasifican en (Kac 1994, Capítulo 4, págs. 47–), específicamente enumerados en (Kac 1994, págs. 53–55). Los diagramas afines se denotan como o donde X es la letra del diagrama finito correspondiente, y el exponente depende de en qué serie de diagramas afines se encuentran. Los primeros de estos, son los más comunes, y se denominan diagramas de Dynkin extendidos y se denotan con una tilde , y también a veces se marcan con un superíndice + . ^[17] como en . Las series (2) y (3) se denominan diagramas afines trenzados . ${\displaystyle X_{l}^{(1)},X_{l}^{(2)},}$ ${\displaystyle X_{l}^{(3)},}$ ${\displaystyle X_{l}^{(1)},}$ ${\displaystyle {\tilde {A}}_{5}=A_{5}^{(1)}=A_{5}^{+}}$

Consulte el generador de diagramas de Dynkin para ver los diagramas.

Aquí se muestran todos los gráficos de Dynkin para grupos afines de hasta 10 nodos. Los gráficos de Dynkin extendidos se dan como familias ~ , al igual que los gráficos finitos anteriores, con un nodo agregado. Otras variaciones de gráficos dirigidos se dan con un valor superíndice (2) o (3), que representa plegamientos de grupos de orden superior. Estos se clasifican como diagramas afines torcidos . ^[18]

Diagramas de Dynkin hiperbólicos y superiores

Se ha enumerado el conjunto de grafos hiperbólicos de Dynkin compactos y no compactos. ^[19] Todos los grafos hiperbólicos de rango 3 son compactos. Los diagramas hiperbólicos de Dynkin compactos existen hasta el rango 5 y los grafos hiperbólicos no compactos existen hasta el rango 10.

Diagramas de Dynkin hiperbólicos compactos

Formas no compactas (sobreextendidas)

Algunas notaciones utilizadas en física teórica , como la teoría M , utilizan un superíndice "+" para grupos extendidos en lugar de un "~" y esto permite definir grupos de extensiones superiores.

1. Los diagramas de Dynkin extendidos (afines) reciben el signo "+" y representan un nodo agregado. (Igual que "~")
2. Los diagramas de Dynkin sobreextendido (hiperbólicos) se indican con "^" o "++" y representan dos nodos agregados.
3. Los diagramas de Dynkin muy extendidos con 3 nodos agregados reciben "+++".

238 Grupos hiperbólicos (compactos y no compactos)

Los 238 grupos hiperbólicos (compactos y no compactos) de rango se nombran y enumeran como para cada rango. ${\displaystyle n\geq 3}$ ${\displaystyle H_{i}^{(n)}}$ ${\displaystyle i=1,2,3...}$

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

Muy extendido

Los grupos muy extendidos son grupos de Lorentz , definidos añadiendo tres nodos a los grupos finitos. Los E ₈ , E ₇ , E ₆ , F ₄ y G ₂ ofrecen seis series que terminan como grupos muy extendidos. Otras series extendidas no mostradas pueden definirse a partir de A _n , B _n , C _n y D _n , como series diferentes para cada n . El determinante de la matriz de Cartan asociada determina dónde la serie cambia de finita (positiva) a afín (cero) a un grupo hiperbólico no compacto (negativo), y termina como un grupo de Lorentz que puede definirse con el uso de una dimensión temporal , y se utiliza en la teoría M. ^[20 ]

Véase también

• Diagrama de Satake
• Lista de índices de Tits irreducibles
• Klassifikation von Wurzelsystemen (Clasificación de sistemas de raíces) (en alemán)

Notas

1. En esta sección nos referimos a la clase general como "diagramas de Coxeter" en lugar de "diagramas de Coxeter-Dynkin" para mayor claridad, ya que existe un gran potencial de confusión y de concisión.
2. Nótese que Stekloshchik utiliza una convención de flecha opuesta a la de este artículo.

Citas

1. Sala 2015 Sección 8.6
2. Hall 2015 Proposiciones 8.6 y 8.13
3. Propuesta 8.6 del Salón 2015
4. Baez, John (13 de abril de 1998), Hallazgos de esta semana en física matemática (semana 119)
5. Fulton y Harris 1991, Proposición D.40
6. Automorfismos externos de álgebras de Lie simples
7. Humphreys 1972, § 16.5
8. Jacobson 1971, § 7
9. Geometría algebraica y teoría de números: en honor al 50.° cumpleaños de Vladimir Drinfeld, editado por Victor Ginzburg, pág. 47, sección 3.6: Plegamiento de grupos
10. Plegado por automorfismos Archivado el 4 de marzo de 2016 en Wayback Machine , John Stembridge, 4pp., 79K, 20 de agosto de 2008, Otros artículos de John Stembridge
11. Véase Stekolshchik 2008, pág. 102, observación 5.4 para ilustraciones de estos pliegues y referencias.
12. Zuber, Jean-Bernard (1998). "Diagramas de Dynkin generalizados y sistemas de raíces y su plegamiento". En Kashiwara, M.; Matsuo, A.; Saito, K.; Satake, I. (eds.). Teoría de campos topológicos, formas primitivas y temas relacionados . Progreso en matemáticas. Vol. 160. págs. 28–30. CiteSeerX 10.1.1.54.3122 . doi :10.1007/978-1-4612-0705-4_16. ISBN .  978-1-4612-6874-1. Número de identificación del sujeto  12429369.
13. Armstrong, John (5 de marzo de 2010). "Transformaciones de los diagramas de Dynkin".
14. Knapp 2002, pág. 758
15. ¿Por qué los diagramas de Dynkin E6, E7 y E8 siempre se dibujan de la forma en que están dibujados?
16. Sección 2.1 en Stekolshchik, Rafael (2005). "Notas sobre las transformaciones de Coxeter y la correspondencia de McKay". arXiv : math/0510216v1 .
17. Véase, por ejemplo, Humphreys, James E. (1990). "48. Dominio fundamental § Grupos de reflexión afines". Grupos de reflexión y grupos de Coxeter . Cambridge University Press. pág. 96. ISBN. 978-0-521-43613-7.
18. Kac, Victor G. (1990). "4. Una clasificación de matrices de Cartan generalizadas". Álgebras de Lie de dimensión infinita . Cambridge University Press. págs. 53–. ISBN 978-0-521-46693-6.
19. Carbone, Lisa; Chung, Sjuvon; Cobbs, Leigh; McRae, Robert; Nandi, Debajyoti; Naqvi, Yusra; Penta, Diego (2010). "Clasificación de diagramas hiperbólicos de Dynkin, longitudes de raíces y órbitas del grupo de Weyl". Journal of Physics A: Mathematical and Theoretical . 43 (15): 155209. arXiv : 1003.0564 . Bibcode :2010JPhA...43o5209C. doi :10.1088/1751-8113/43/15/155209. S2CID  16946456.
20. Englert, François; Houart, Laurent; Taormina, Anne ; West, Peter (2003). "La simetría de las teorías M". Journal of High Energy Physics . 2003 (9): 020. arXiv : hep-th/0304206 . Código Bibliográfico :2003JHEP...09..020E. doi :10.1088/1126-6708/2003/09/020. S2CID  15680493.

Referencias

• Dynkin, EB (1947), "La estructura de las álgebras semisimples", Uspekhi Mat. Nauk , NS (en ruso), 2 (4(20)): 59–127
• Bourbaki, Nicolas (1968), "Capítulos 4 a 6", Groupes et algebres de Lie , París: Hermann
• Jacobson, Nathan (1 de junio de 1971), Álgebras de Lie excepcionales , CRC Press, ISBN 978-0-8247-1326-3
• Humphreys, James E. (1972), Introducción a las álgebras de Lie y la teoría de la representación , Birkhäuser, ISBN 978-0-387-90053-7
• Fulton, William ; Harris, Joe (1991). Teoría de la representación. Un primer curso . Textos de posgrado en matemáticas , Lecturas en matemáticas. Vol. 129. Nueva York: Springer-Verlag. doi :10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. Sr.  1153249. OCLC  246650103.
• Dynkin, Evgeniĭ Borisovich; Alexander Adolph Yushkevich; Gary M. Seitz; AL Onishchik (2000), Artículos seleccionados de EB Dynkin con comentarios , Librería AMS, ISBN 978-0-8218-1065-1
• Hall, Brian C. (2015), Grupos de Lie, álgebras de Lie y representaciones: una introducción elemental , Textos de posgrado en matemáticas, vol. 222 (2.ª ed.), Springer, ISBN 978-3319134666
• Knapp, Anthony W. (2002), Grupos de Lie más allá de una introducción (2.ª ed.), Birkhäuser, ISBN 978-0-8176-4259-4
• Stekolshchik, R. (2008), Notas sobre las transformaciones de Coxeter y la correspondencia de McKay , Springer Monographs in Mathematics, arXiv : math/0510216 , doi :10.1007/978-3-540-77399-3, ISBN 978-3-540-77398-6, Número de identificación del sujeto  117958873
• Carbone, Lisa; Chung, Sjuvon; Cobbs, Leigh; Mcrae, Robert; Nandi, Debajyoti; Navqi, Yusra; Penta, Diego (marzo de 2010), "Clasificación de diagramas hiperbólicos de Dynkin, longitudes de raíces y órbitas del grupo de Weyl". (PDF) , Journal of Physics A: Mathematical and Theoretical , 43 (15): 155209, arXiv : 1003.0564 , Bibcode :2010JPhA...43o5209C, doi :10.1088/1751-8113/43/15/155209, MR  2608277, S2CID  16946456
• Kac, Victor G. (1994). Álgebras de Lie de dimensión infinita. Cambridge University Press. ISBN 978-0-521-46693-6.
• Dynkin, Eugene B. (2000). Yushkevich, AA; Seitz , GM; Onishchik, AL (eds.). Artículos seleccionados de EB Dynkin con comentarios. Providence, RI: American Mathematical Society. ISBN 978-0-8218-1065-1.Sr. 1757976  .

Enlaces externos

• John Baez sobre la ubicuidad de los diagramas de Dynkin en las matemáticas
• Herramienta web para crear diagramas de Dynkin con etiquetas y calidad de publicación (escritos en JavaScript)