El efecto Magnus es un fenómeno que se produce cuando un objeto giratorio se mueve a través de un fluido . Una fuerza de sustentación actúa sobre el objeto giratorio y su trayectoria puede desviarse de una manera que no ocurre cuando no está girando. La fuerza y la dirección del efecto Magnus dependen de la velocidad y la dirección de la rotación del objeto. [1]
El efecto Magnus recibe su nombre de Heinrich Gustav Magnus , el físico alemán que lo investigó. La fuerza sobre un cilindro giratorio es un ejemplo de sustentación de Kutta-Joukowski , [2] llamada así por Martin Kutta y Nikolay Zhukovsky (o Joukowski), matemáticos que contribuyeron al conocimiento de cómo se genera la sustentación en un flujo de fluido. [3]
El caso más fácilmente observable del efecto Magnus es cuando una esfera (o cilindro) que gira se curva alejándose del arco que seguiría si no estuviera girando. Lo utilizan a menudo los jugadores de fútbol ( soccer ) y voleibol , los lanzadores de béisbol y los jugadores de críquet . En consecuencia, el fenómeno es importante en el estudio de la física de muchos deportes de pelota . También es un factor importante en el estudio de los efectos del giro en los misiles guiados , y tiene algunos usos de ingeniería, por ejemplo, en el diseño de barcos de rotor y aviones Flettner .
El topspin en los juegos de pelota se define como un giro sobre un eje horizontal perpendicular a la dirección de desplazamiento que mueve la superficie superior de la pelota en la dirección de desplazamiento. Bajo el efecto Magnus, el topspin produce un giro hacia abajo de una pelota en movimiento, mayor que el que se produciría solo por la gravedad. El backspin produce una fuerza hacia arriba que prolonga el vuelo de una pelota en movimiento. [4] Del mismo modo, el sidespin causa un giro hacia ambos lados como se ve durante algunos lanzamientos de béisbol, por ejemplo, slider . [5] El comportamiento general es similar al que se produce alrededor de un perfil aerodinámico (ver fuerza de sustentación ), pero con una circulación generada por la rotación mecánica en lugar de la forma del perfil. [6]
En el béisbol, este efecto se utiliza para generar el movimiento descendente de una bola curva, en la que la pelota gira hacia adelante (con efecto "topspin"). Los participantes de otros deportes en los que se juega con pelota también aprovechan este efecto.
El efecto Magnus o fuerza Magnus actúa sobre un cuerpo giratorio que se mueve en relación con un fluido. Algunos ejemplos incluyen una " bola curva " en el béisbol o una pelota de tenis golpeada oblicuamente. La rotación altera la capa límite entre el objeto y el fluido. La fuerza es perpendicular a la dirección relativa del movimiento y está orientada hacia la dirección de rotación, es decir, la dirección hacia la que gira la "punta" de la pelota. [7] La magnitud de la fuerza depende principalmente de la velocidad de rotación, la velocidad relativa y la geometría del cuerpo; la magnitud también depende de la rugosidad de la superficie del cuerpo y de la viscosidad del fluido. Las predicciones cuantitativas precisas de la fuerza son difíciles, [7] : 20 pero, como con otros ejemplos de sustentación aerodinámica, existen explicaciones cualitativas más simples :
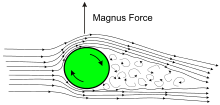
El diagrama muestra la sustentación que se produce en una pelota que gira hacia atrás. La estela y el flujo de aire que la sigue se desvían hacia abajo; según la tercera ley de movimiento de Newton, debe haber una fuerza de reacción en la dirección opuesta. [1] [8]
La viscosidad del aire y la rugosidad de la superficie del objeto hacen que el aire se mueva alrededor del objeto, lo que aumenta la velocidad del aire en un lado del objeto y disminuye la velocidad en el otro lado. El principio de Bernoulli establece que, en determinadas condiciones, el aumento de la velocidad del flujo se asocia con una reducción de la presión, lo que implica que hay una menor presión de aire en un lado que en el otro. Esta diferencia de presión da como resultado una fuerza perpendicular a la dirección de desplazamiento. [9]

En un cilindro, la fuerza debida a la rotación es un ejemplo de sustentación de Kutta-Joukowski . Puede analizarse en términos del vórtice producido por la rotación. La sustentación por unidad de longitud del cilindro es el producto de la velocidad de la corriente libre (en m/s), la densidad del fluido (en kg/m 3 ) y la circulación debida a los efectos viscosos: [2]
donde la fuerza del vórtice (asumiendo que el fluido circundante obedece la condición de no deslizamiento ) viene dada por
donde ω es la velocidad angular del cilindro (en rad/s) y r es el radio del cilindro (en m).
En estudios en túneles de viento , las pelotas de béisbol (de superficie rugosa) muestran el efecto Magnus, pero las esferas lisas no. [10] Estudios posteriores han demostrado que ciertas combinaciones de condiciones dan como resultado turbulencia en el fluido en un lado del cuerpo giratorio, pero flujo laminar en el otro lado. [11] En estos casos se denomina efecto Magnus inverso: la desviación es opuesta a la del efecto Magnus típico. [12]
El flujo potencial es un modelo matemático del flujo constante de un fluido sin viscosidad ni vorticidad . Para el flujo potencial alrededor de un cilindro circular, proporciona los siguientes resultados:

El patrón de flujo es simétrico respecto de un eje horizontal que pasa por el centro del cilindro. En cada punto por encima del eje y su punto correspondiente por debajo del eje, el espaciamiento de las líneas de corriente es el mismo, por lo que las velocidades también son las mismas en los dos puntos. El principio de Bernoulli muestra que, fuera de las capas límite , las presiones también son las mismas en los puntos correspondientes. No hay sustentación actuando sobre el cilindro. [13]

Las líneas de corriente están más próximas entre sí inmediatamente por encima del cilindro que por debajo, de modo que el aire fluye más rápido por la superficie superior que por la inferior. El principio de Bernoulli demuestra que la presión adyacente a la superficie superior es menor que la presión adyacente a la superficie inferior. La fuerza de Magnus actúa verticalmente hacia arriba sobre el cilindro. [14]
Las líneas de corriente inmediatamente por encima del cilindro están curvadas con un radio apenas mayor que el radio del cilindro. Esto significa que hay baja presión cerca de la superficie superior del cilindro. Las líneas de corriente inmediatamente debajo del cilindro están curvadas con un radio mayor que las líneas de corriente por encima del cilindro. Esto significa que hay una mayor presión actuando sobre la superficie inferior que sobre la superior. [15]
El aire que se encuentra inmediatamente por encima y por debajo del cilindro se curva hacia abajo, acelerado por el gradiente de presión. Una fuerza descendente actúa sobre el aire.
La tercera ley de Newton predice que la fuerza Magnus y la fuerza hacia abajo que actúa sobre el aire son iguales en magnitud y opuestas en dirección.
El efecto recibe su nombre del físico alemán Heinrich Gustav Magnus , quien demostró el efecto con un cilindro de latón que giraba rápidamente y un soplador de aire en 1852. [16] [17] [7] : 18 En 1672, Isaac Newton había especulado sobre el efecto después de observar a los jugadores de tenis en su universidad de Cambridge . [18] [19] En 1742, Benjamin Robins , un matemático británico, investigador balístico e ingeniero militar, explicó las desviaciones en las trayectorias de las balas de mosquete debido a su rotación. [20] [21] [22] [23]
En 1928 se llevaron a cabo investigaciones pioneras en túneles de viento sobre el efecto Magnus con esferas giratorias suaves . [24] Posteriormente, Lyman Briggs estudió pelotas de béisbol en un túnel de viento, [10] y otros han producido imágenes del efecto. [25] [26] [12] Los estudios muestran que una estela turbulenta detrás de la pelota giratoria provoca una resistencia aerodinámica, además de que hay una desviación angular notable en la estela, y esta desviación va en la dirección del giro.


El efecto Magnus explica las desviaciones comúnmente observadas de las trayectorias o caminos típicos de las pelotas giratorias en los deportes , en particular el fútbol , el tenis de mesa , [27] el tenis , [28] el voleibol , el golf , el béisbol y el cricket .
La trayectoria curva de una pelota de golf, conocida como slice o hook, se debe en gran medida a que el eje de giro de la pelota está inclinado lejos de la horizontal debido a los efectos combinados del ángulo de la cara del palo y la trayectoria del swing, lo que hace que el efecto Magnus actúe en un ángulo, alejando la pelota de una línea recta en su trayectoria. [29] El backspin (superficie superior que gira hacia atrás desde la dirección del movimiento) en una pelota de golf provoca una fuerza vertical que contrarresta ligeramente la fuerza de la gravedad y permite que la pelota permanezca en el aire un poco más de lo que permanecería si la pelota no girara: esto permite que la pelota viaje más lejos que una pelota que no gira sobre su eje horizontal. [ cita requerida ]
En el tenis de mesa , el efecto Magnus se observa fácilmente debido a la pequeña masa y baja densidad de la pelota. Un jugador experimentado puede aplicar una amplia variedad de efectos a la pelota. Las raquetas de tenis de mesa suelen tener una superficie de goma para que la raqueta tenga el máximo agarre sobre la pelota y le dé un efecto.
En el cricket , el efecto Magnus contribuye a los tipos de movimiento conocidos como deriva , inmersión y elevación en los bolos con spin , dependiendo del eje de rotación del spin aplicado a la bola. El efecto Magnus no es responsable del movimiento observado en los bolos con swing convencionales , [30] : Fig. 4.19 en el que el gradiente de presión no es causado por el giro de la bola, sino más bien por su costura elevada y la rugosidad o suavidad asimétrica de sus dos mitades; sin embargo, el efecto Magnus puede ser responsable del llamado "Malinga Swing", [31] [32] como se observa en el lanzamiento del lanzador con swing Lasith Malinga .
En airsoft , se utiliza un sistema conocido como hop-up para crear un efecto retroceso en una bola disparada , lo que aumenta enormemente su alcance, utilizando el efecto Magnus de manera similar al golf.
En el béisbol , los lanzadores suelen aplicar distintos giros a la pelota, lo que hace que se curve en la dirección deseada debido al efecto Magnus. El sistema PITCHf/x mide el cambio de trayectoria causado por el efecto Magnus en todos los lanzamientos realizados en las Grandes Ligas de Béisbol . [33]
El balón de la Copa Mundial de la FIFA 2010 ha sido criticado por el efecto Magnus, diferente al de los balones anteriores. Se ha dicho que el balón tiene menos efecto Magnus y, como resultado, vuela más lejos pero con un viraje menos controlable. [34]
El efecto Magnus también se puede encontrar en balística externa avanzada . En primer lugar, una bala que gira en vuelo a menudo está sujeta a un viento cruzado , que se puede simplificar diciendo que sopla desde la izquierda o la derecha. Además de esto, incluso en aire completamente en calma, una bala experimenta un pequeño componente de viento lateral debido a su movimiento de guiñada . Este movimiento de guiñada a lo largo de la trayectoria de vuelo de la bala significa que la punta de la bala apunta en una dirección ligeramente diferente de la dirección en la que viaja la bala. En otras palabras, la bala "se desliza" lateralmente en un momento dado y, por lo tanto, experimenta un pequeño componente de viento lateral además de cualquier componente de viento cruzado. [35]
El componente combinado del viento lateral de estos dos efectos hace que una fuerza Magnus actúe sobre la bala, que es perpendicular tanto a la dirección en la que apunta la bala como al viento lateral combinado. En un caso muy simple en el que ignoramos varios factores que complican la situación, la fuerza Magnus del viento cruzado provocaría una fuerza hacia arriba o hacia abajo que actuaría sobre la bala que gira (dependiendo del viento y la rotación hacia la izquierda o hacia la derecha), lo que provocaría una desviación de la trayectoria de vuelo de la bala hacia arriba o hacia abajo, lo que influiría en el punto de impacto.
En general, el efecto de la fuerza Magnus en la trayectoria de vuelo de una bala suele ser insignificante en comparación con otras fuerzas como la resistencia aerodinámica . Sin embargo, afecta en gran medida a la estabilidad de la bala, que a su vez afecta a la cantidad de resistencia, cómo se comporta la bala al impactar y muchos otros factores. La estabilidad de la bala se ve afectada, porque el efecto Magnus actúa sobre el centro de presión de la bala en lugar de su centro de gravedad . [36] Esto significa que afecta al ángulo de guiñada de la bala; tiende a torcer la bala a lo largo de su trayectoria de vuelo, ya sea hacia el eje de vuelo (disminuyendo la guiñada y estabilizando así la bala) o lejos del eje de vuelo (aumentando la guiñada y desestabilizando así la bala). El factor crítico es la ubicación del centro de presión, que depende de la estructura del campo de flujo, que a su vez depende principalmente de la velocidad de la bala (supersónica o subsónica), pero también de la forma, la densidad del aire y las características de la superficie. Si el centro de presión está por delante del centro de gravedad, el efecto es desestabilizador; si el centro de presión está por detrás del centro de gravedad, el efecto es estabilizador. [37]

Se han construido algunos aviones que utilizan el efecto Magnus para crear sustentación con un cilindro giratorio en lugar de un ala, lo que permite volar a velocidades horizontales más bajas. [2] El primer intento de utilizar el efecto Magnus para un avión más pesado que el aire fue en 1910 por un miembro del Congreso de los EE. UU., Butler Ames de Massachusetts. El siguiente intento fue a principios de la década de 1930 por parte de tres inventores en el estado de Nueva York. [38]

Los barcos de rotor utilizan cilindros similares a mástiles, llamados rotores Flettner , para la propulsión. Estos están montados verticalmente en la cubierta del barco. Cuando el viento sopla desde un lado, el efecto Magnus crea un empuje hacia adelante. Por lo tanto, como ocurre con cualquier barco de vela, un barco de rotor solo puede moverse hacia adelante cuando sopla el viento. El efecto también se utiliza en un tipo especial de estabilizador de barco que consiste en un cilindro giratorio montado debajo de la línea de flotación y que emerge lateralmente. Al controlar la dirección y la velocidad de rotación, se puede generar una fuerte sustentación o carga aerodinámica . [39] El mayor despliegue del sistema hasta la fecha se encuentra en el yate a motor Eclipse .
El resultado es que la estela no es simétrica; el flujo de aire se desvía hacia un lado y la esfera experimenta una fuerza de reacción en la dirección opuesta... La dirección y la intensidad de esta fuerza dependerán de la velocidad y la dirección del giro. Este fenómeno se conoce como el efecto Magnus...
La sustentación se produce cuando un flujo de gas en movimiento gira por acción de un objeto sólido. El flujo gira en una dirección y la sustentación se genera en la dirección opuesta, según la tercera ley de acción y reacción de Newton.
Sin la viscosidad y la capa límite, la bola giratoria no podría transportar aire de esta manera... la velocidad del aire debajo de la bola es menor que la que está por encima de ella. Según la ecuación de Bernoulli, la presión del aire debajo de la bola debe ser mayor que la que está por encima, por lo que la bola experimenta una fuerza de sustentación dinámica.
...si una línea de corriente es curva, debe haber un gradiente de presión a través de la línea de corriente
{{cite book}}: CS1 maint: location missing publisher (link){{cite book}}: CS1 maint: location missing publisher (link)