Potencial delta

Modelo de un potencial energético en mecánica cuántica

En mecánica cuántica, el potencial delta es un potencial que se describe matemáticamente mediante la función delta de Dirac , una función generalizada . Cualitativamente, corresponde a un potencial que es cero en todas partes, excepto en un único punto, donde toma un valor infinito. Esto se puede utilizar para simular situaciones en las que una partícula es libre de moverse en dos regiones del espacio con una barrera entre las dos regiones. Por ejemplo, un electrón puede moverse casi libremente en un material conductor, pero si se colocan dos superficies conductoras juntas, la interfaz entre ellas actúa como una barrera para el electrón que se puede aproximar mediante un potencial delta.

El pozo de potencial delta es un caso límite del pozo de potencial finito , que se obtiene si se mantiene constante el producto del ancho del pozo por el potencial mientras se disminuye el ancho del pozo y se aumenta el potencial.

Este artículo, para simplificar, sólo considera un pozo potencial unidimensional, pero el análisis podría ampliarse a más dimensiones.

Potencial delta único

La ecuación de Schrödinger independiente del tiempo para la función de onda ψ ( x ) de una partícula en una dimensión en un potencial V ( x ) es donde ħ es la constante de Planck reducida y E es la energía de la partícula. $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x),}$$

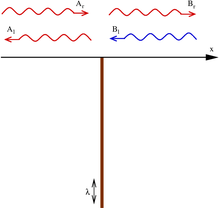
El potencial delta es el potencial donde δ ( x ) es la función delta de Dirac . $${\displaystyle V(x)=\lambda \delta (x),}$$

Se denomina pozo de potencial delta si λ es negativo y barrera de potencial delta si λ es positivo. Para simplificar, se ha definido que el delta se produce en el origen; un cambio en el argumento de la función delta no cambia ninguno de los siguientes resultados.

Resolviendo la ecuación de Schrödinger

Fuente: ^[1]

El potencial divide el espacio en dos partes ( x < 0 y x > 0 ). En cada una de estas partes el potencial es cero, y la ecuación de Schrödinger se reduce a que es una ecuación diferencial lineal con coeficientes constantes , cuyas soluciones son combinaciones lineales de e ^ikx y e ^{− ikx} , donde el número de onda k está relacionado con la energía por $${\displaystyle {\frac {d^{2}\psi }{dx^{2}}}=-{\frac {2mE}{\hbar ^{2}}}\psi ;}$$ $${\displaystyle k={\frac {\sqrt {2mE}}{\hbar }}.}$$

En general, debido a la presencia del potencial delta en el origen, los coeficientes de la solución no necesitan ser los mismos en ambos semiespacios: donde, en el caso de energías positivas ( k real ), e ^ikx representa una onda que viaja hacia la derecha, y e ^{− ikx} una que viaja hacia la izquierda. $${\displaystyle \psi (x)={\begin{cases}\psi _{\text{L}}(x)=A_{\text{r}}e^{ikx}+A_{\text{l}}e^{-ikx},&{\text{ if }}x<0,\\\psi _{\text{R}}(x)=B_{\text{r}}e^{ikx}+B_{\text{l}}e^{-ikx},&{\text{ if }}x>0,\end{cases}}}$$

Se obtiene una relación entre los coeficientes imponiendo que la función de onda sea continua en el origen: $${\displaystyle \psi (0)=\psi _{L}(0)=\psi _{R}(0)=A_{r}+A_{l}=B_{r}+B_{l},}$$

Se puede encontrar una segunda relación estudiando la derivada de la función de onda. Normalmente, también podríamos imponer la diferenciabilidad en el origen, pero esto no es posible debido al potencial delta. Sin embargo, si integramos la ecuación de Schrödinger alrededor de x = 0 , en un intervalo [− ε , + ε ] : $${\displaystyle -{\frac {\hbar ^{2}}{2m}}\int _{-\varepsilon }^{+\varepsilon }\psi ''(x)\,dx+\int _{-\varepsilon }^{+\varepsilon }V(x)\psi (x)\,dx=E\int _{-\varepsilon }^{+\varepsilon }\psi (x)\,dx.}$$

En el límite cuando ε → 0 , el lado derecho de esta ecuación se desvanece; el lado izquierdo se convierte en porque Sustituyendo la definición de ψ en esta expresión se obtiene $${\displaystyle -{\frac {\hbar ^{2}}{2m}}[\psi _{R}'(0)-\psi _{L}'(0)]+\lambda \psi (0),}$$ $${\displaystyle \int _{-\varepsilon }^{+\varepsilon }\psi ''(x)\,dx=[\psi '(+\varepsilon )-\psi '(-\varepsilon )].}$$ $${\displaystyle -{\frac {\hbar ^{2}}{2m}}ik(-A_{r}+A_{l}+B_{r}-B_{l})+\lambda (A_{r}+A_{l})=0.}$$

Las condiciones de contorno dan lugar, por tanto, a las siguientes restricciones sobre los coeficientes $${\displaystyle {\begin{cases}A_{r}+A_{l}-B_{r}-B_{l}&=0,\\-A_{r}+A_{l}+B_{r}-B_{l}&={\frac {2m\lambda }{ik\hbar ^{2}}}(A_{r}+A_{l}).\end{cases}}}$$

Estado ligado (mi< 0)

La gráfica de la solución de la función de onda del estado ligado al potencial de la función delta es continua en todas partes, pero su derivada no está definida en x = 0 .

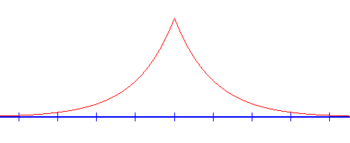
En cualquier potencial atractivo unidimensional habrá un estado ligado . Para hallar su energía, observe que para E < 0 , k = i √ 2 m | E | / ħ = iκ es imaginaria, y las funciones de onda que oscilaban para energías positivas en el cálculo anterior ahora son funciones exponencialmente crecientes o decrecientes de x (ver arriba). Al exigir que las funciones de onda no diverjan en el infinito se elimina la mitad de los términos: A _r = B _l = 0 . La función de onda es entonces $${\displaystyle \psi (x)={\begin{cases}\psi _{\text{L}}(x)=A_{\text{l}}e^{\kappa x},&{\text{ if }}x\leq 0,\\\psi _{\text{R}}(x)=B_{\text{r}}e^{-\kappa x},&{\text{ if }}x\geq 0.\end{cases}}}$$

De las condiciones de contorno y de normalización se deduce que λ debe ser negativo, es decir, el estado límite solo existe para el pozo, y no para la barrera. La transformada de Fourier de esta función de onda es una función de Lorentz . $${\displaystyle {\begin{cases}A_{\text{l}}=B_{\text{r}}={\sqrt {\kappa }},\\\kappa =-{\frac {m\lambda }{\hbar ^{2}}},\end{cases}}}$$

La energía del estado ligado es entonces $${\displaystyle E=-{\frac {\hbar ^{2}\kappa ^{2}}{2m}}=-{\frac {m\lambda ^{2}}{2\hbar ^{2}}}.}$$

Dispersión (mi> 0)

Probabilidad de transmisión ( T ) y reflexión ( R ) de un pozo de potencial delta. La energía E > 0 está en unidades de . Línea discontinua: resultado clásico. Línea continua: mecánica cuántica. ${\displaystyle {\frac {m\lambda ^{2}}{2\hbar ^{2}}}}$

Para energías positivas, la partícula es libre de moverse en cualquier semiespacio: x < 0 o x > 0. Puede dispersarse en el potencial de la función delta.

El caso cuántico puede estudiarse en la siguiente situación: una partícula incide sobre la barrera desde el lado izquierdo ( A _r ) . Puede reflejarse ( A _l ) o transmitirse ( B _r ) . Para encontrar las amplitudes de reflexión y transmisión para la incidencia desde la izquierda, ponemos en las ecuaciones anteriores A _r = 1 (partícula entrante), A _l = r (reflexión), B _l = 0 (no hay partícula entrante desde la derecha) y B _r = t (transmisión), y resolvemos para r y t aunque no tenemos ninguna ecuación en t . El resultado es $${\displaystyle t={\cfrac {1}{1-{\cfrac {m\lambda }{i\hbar ^{2}k}}}},\quad r={\cfrac {1}{{\cfrac {i\hbar ^{2}k}{m\lambda }}-1}}.}$$

Debido a la simetría especular del modelo, las amplitudes de incidencia desde la derecha son las mismas que las de la izquierda. El resultado es que existe una probabilidad distinta de cero de que la partícula se refleje. Esto no depende del signo de λ , es decir, una barrera tiene la misma probabilidad de reflejar la partícula que un pozo. Esta es una diferencia significativa con respecto a la mecánica clásica, donde la probabilidad de reflexión sería 1 para la barrera (la partícula simplemente rebota) y 0 para el pozo (la partícula pasa a través del pozo sin perturbaciones). $${\displaystyle R=|r|^{2}={\cfrac {1}{1+{\cfrac {\hbar ^{4}k^{2}}{m^{2}\lambda ^{2}}}}}={\cfrac {1}{1+{\cfrac {2\hbar ^{2}E}{m\lambda ^{2}}}}}}$$

La probabilidad de transmisión es $${\displaystyle T=|t|^{2}=1-R={\cfrac {1}{1+{\cfrac {m^{2}\lambda ^{2}}{\hbar ^{4}k^{2}}}}}={\cfrac {1}{1+{\cfrac {m\lambda ^{2}}{2\hbar ^{2}E}}}}.}$$

Observaciones y aplicación

El cálculo presentado anteriormente puede parecer poco realista y poco útil en un principio, pero ha demostrado ser un modelo adecuado para una variedad de sistemas de la vida real.

Un ejemplo de ello se refiere a las interfaces entre dos materiales conductores . En la mayor parte de los materiales, el movimiento de los electrones es casi libre y puede describirse mediante el término cinético del hamiltoniano anterior con una masa efectiva m . A menudo, las superficies de dichos materiales están cubiertas de capas de óxido o no son ideales por otras razones. Esta capa delgada y no conductora puede entonces modelarse mediante un potencial de función delta local como el anterior. Los electrones pueden entonces pasar de un material a otro dando lugar a una corriente.

El funcionamiento de un microscopio de efecto túnel (STM) se basa en este efecto túnel. En ese caso, la barrera se debe al aire que hay entre la punta del STM y el objeto subyacente. La fuerza de la barrera está relacionada con la separación, que es mayor cuanto más separados están los dos. Para un modelo más general de esta situación, consulte Barrera de potencial finita (QM) . La barrera de potencial de función delta es el caso límite del modelo considerado allí para barreras muy altas y estrechas.

El modelo anterior es unidimensional, mientras que el espacio que nos rodea es tridimensional. De hecho, la ecuación de Schrödinger debería resolverse en tres dimensiones. Por otra parte, muchos sistemas sólo cambian a lo largo de una dirección de coordenadas y son invariantes en la traslación a lo largo de las demás. La ecuación de Schrödinger puede entonces reducirse al caso considerado aquí mediante un Ansatz para la función de onda del tipo . ${\displaystyle \Psi (x,y,z)=\psi (x)\phi (y,z)\,\!}$

Alternativamente, es posible generalizar la función delta para que exista en la superficie de algún dominio D (ver Laplaciano del indicador ). ^[2]

El modelo de función delta es en realidad una versión unidimensional del átomo de hidrógeno según el método de escala dimensional desarrollado por el grupo de Dudley R. Herschbach ^[3] El modelo de función delta se vuelve particularmente útil con el modelo de función delta de Dirac de doble pozo que representa una versión unidimensional del ion de la molécula de hidrógeno , como se muestra en la siguiente sección.

Potencial de doble delta

Funciones de onda simétricas y antisimétricas para el modelo de función delta de Dirac de doble pozo con distancia "internuclear" R = 2

La función delta de Dirac de doble pozo modela una molécula de hidrógeno diatómico mediante la ecuación de Schrödinger correspondiente: donde el potencial es ahora donde es la distancia "internuclear" con picos (negativos) de la función delta de Dirac ubicados en x = ± R /2 (mostrados en marrón en el diagrama). Teniendo en cuenta la relación de este modelo con su contraparte molecular tridimensional, usamos unidades atómicas y establecemos . Aquí hay un parámetro formalmente ajustable. Del caso de pozo único, podemos inferir que el " ansatz " para la solución es La coincidencia de la función de onda en los picos de la función delta de Dirac produce el determinante Por lo tanto, se encuentra que está gobernada por la ecuación pseudo-cuadrática que tiene dos soluciones . Para el caso de cargas iguales (caso homonuclear simétrico), λ = 1 , y la pseudo-cuadrática se reduce a El caso "+" corresponde a una función de onda simétrica respecto del punto medio (mostrado en rojo en el diagrama), donde A = B , y se llama gerade . En consecuencia, el caso "−" es la función de onda que es antisimétrica respecto del punto medio, donde A = − B , y se denomina ungerade (mostrado en verde en el diagrama). Representan una aproximación de los dos estados de energía discretos más bajos del tridimensional y son útiles en su análisis. Las soluciones analíticas para los valores propios de energía para el caso de cargas simétricas se dan por ^[4] donde W es la función W de Lambert estándar . Nótese que la energía más baja corresponde a la solución simétrica . En el caso de cargas desiguales , y por lo tanto del problema molecular tridimensional, las soluciones se dan por una generalización de la función W de Lambert (ver Función W de Lambert § Generalizaciones ). $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x),}$$ $${\displaystyle V(x)=-q\left[\delta \left(x+{\frac {R}{2}}\right)+\lambda \delta \left(x-{\frac {R}{2}}\right)\right],}$$ ${\displaystyle 0<R<\infty }$ ${\displaystyle \hbar =m=1}$ ${\displaystyle 0<\lambda <1}$ $${\displaystyle \psi (x)=Ae^{-d\left|x+{\frac {R}{2}}\right|}+Be^{-d\left|x-{\frac {R}{2}}\right|}.}$$ $${\displaystyle {\begin{vmatrix}q-d&qe^{-dR}\\q\lambda e^{-dR}&q\lambda -d\end{vmatrix}}=0,\quad {\text{where }}E=-{\frac {d^{2}}{2}}.}$$ ${\displaystyle d}$ $${\displaystyle d_{\pm }(\lambda )={\frac {1}{2}}q(\lambda +1)\pm {\frac {1}{2}}\left\{q^{2}(1+\lambda )^{2}-4\lambda q^{2}\left[1-e^{-2d_{\pm }(\lambda )R}\right]\right\}^{1/2},}$$ ${\displaystyle d=d_{\pm }}$ $${\displaystyle d_{\pm }=q\left[1\pm e^{-d_{\pm }R}\right].}$$ ${\displaystyle {\ce {H2^+}}}$ $${\displaystyle d_{\pm }=q+W(\pm qRe^{-qR})/R,}$$ ${\displaystyle d_{+}}$

Uno de los casos más interesantes es cuando qR  ≤ 1, lo que da como resultado . Por lo tanto, se tiene una solución de estado ligado no trivial con E = 0 . Para estos parámetros específicos, se producen muchas propiedades interesantes, una de las cuales es el efecto inusual de que el coeficiente de transmisión es la unidad en energía cero. ^[5] ${\displaystyle d_{-}=0}$

Véase también

• Partícula libre
• Partícula en una caja
• Pozo de potencial finito
• Partícula en un anillo
• Partícula en un potencial simétrico esférico
• Oscilador armónico cuántico
• Átomo de hidrógeno o átomo parecido al hidrógeno
• Guía de ondas en anillo
• Partícula en una red unidimensional (potencial periódico)
• Ion molecular de hidrógeno
• Método Holstein-Herring
• Laplaciano del indicador
• Lista de sistemas mecánico-cuánticos con soluciones analíticas

Referencias

1. "mecánica cuántica - Función de onda con un potencial delta". Physics Stack Exchange . Consultado el 29 de marzo de 2021 .
2. Lange, Rutger-Jan (2012), "Teoría del potencial, integrales de trayectoria y el laplaciano del indicador", Journal of High Energy Physics , 2012 (11): 1–49, arXiv : 1302.0864 , Bibcode :2012JHEP...11..032L, doi :10.1007/JHEP11(2012)032, S2CID  56188533
3. DR Herschbach , JS Avery y O. Goscinski (eds.), Escalamiento dimensional en física química , Springer, (1992). [1]
4. T. C. Scott, J. F. Babb, A. Dalgarno y John D. Morgan III, "El cálculo de las fuerzas de intercambio: resultados generales y modelos específicos", J. Chem. Phys. , 99, págs. 2841–2854, (1993).
5. van Dijk, W.; Kiers, KA (1992). "Retardo temporal en sistemas unidimensionales simples". Revista estadounidense de física . 60 (6). Asociación estadounidense de profesores de física (AAPT): 520–527. Código bibliográfico :1992AmJPh..60..520V. doi :10.1119/1.16866. ISSN  0002-9505.

• Griffiths, David J. (2005). Introducción a la mecánica cuántica (2.ª ed.). Prentice Hall. pp. 68–78. ISBN 978-0-13-111892-8.
• Para el caso tridimensional, busque el "potencial de capa delta"; véase también K. Gottfried (1966), Mecánica cuántica, volumen I: fundamentos , cap. III, sec. 15.

Enlaces externos

• Medios relacionados con el potencial del Delta en Wikimedia Commons