stringtranslate.com

Enlace de cuatro barras

En el estudio de mecanismos , un eslabón de cuatro barras , también llamado de cuatro barras , es el eslabón móvil de cadena cerrada más simple . Consiste en cuatro cuerpos , llamados barras o eslabones , conectados en un bucle por cuatro articulaciones . Generalmente, las articulaciones están configuradas de modo que los eslabones se muevan en planos paralelos, y el conjunto se denomina eslabón plano de cuatro barras . También existen eslabonamientos de cuatro barras esféricos y espaciales que se utilizan en la práctica. [1]

El mecanismo principal de un balancín es un mecanismo de cuatro barras.

Enlace plano de cuatro barras

Curvas de acoplamiento de un mecanismo de cuatro barras de cigüeñal y balancín. Simulación realizada con MeKin2D.
Un ejemplo de un enlace RRRP o de manivela deslizante .
Un ejemplo de un mecanismo de manivela-deslizador invertido (RRPR) .

Los eslabones planos de cuatro barras se construyen a partir de cuatro eslabones conectados en un bucle mediante cuatro juntas de un grado de libertad . Una junta puede ser una junta giratoria , también conocida como junta de pasador o junta articulada, denotada por R, o una junta prismática , también conocida como par deslizante, denotada por P. [Nota 1]

Un enlace que está fijo en su lugar en relación con el espectador se llama enlace de tierra.
Un enlace que se conecta al suelo mediante una junta giratoria que puede realizar una revolución completa se llama enlace de manivela .
Un enlace que se conecta al suelo mediante una junta giratoria que no puede realizar una revolución completa se llama enlace de balancín.
Un enlace que se conecta a una línea de tierra mediante una junta prismática se llama deslizador. Los deslizadores a veces se consideran manivelas que tienen un pivote articulado a una distancia infinitamente larga perpendicular al recorrido del deslizador.
Un enlace que se conecta a otros dos enlaces se llama enlace flotante o acoplador. Un acoplador que conecta una manivela y un deslizador en un solo mecanismo de manivela deslizante a menudo se llama biela , sin embargo, también se ha utilizado para referirse a cualquier tipo de acoplador.

Existen tres tipos básicos de articulación plana de cuatro barras, dependiendo del uso de juntas prismáticas o giratorias:

  1. Articulaciones de cuatro giros:
    Se denomina RRRR y está formada por cuatro eslabones conectados por cuatro articulaciones de giro. El eslabonamiento cuadrilátero plano se refiere a todas las disposiciones de este tipo.
    Algunos ejemplos de eslabones 4R son:
    • Articulación de doble manivela
    • Articulación de manivela-balancín (pedal) (utilizada en motobombas )
    • Varillaje de doble balancín (utilizado en la dirección Ackermann )
    • Vínculos de Paralelogramo (Movimiento Paralelo [Nota 2] ) y Antiparalelogramo (Contraparalelogramo, Paralelogramo Inverso, Mariposa, Moño)
    • Enlaces deltoides (Galloway) y trapecio (Arglin)
  2. Articulaciones de tres ejes:
    Se denomina RRRP, PRRR, RPRR o RRPR y está formada por cuatro eslabones conectados por tres articulaciones de tres ejes y una articulación prismática. El mecanismo de corredera-manivela (RRRP) es un tipo de disposición en la que un eslabón es una manivela, que luego se conecta a una corredera mediante una biela. La corredera-manivela invertida es otro tipo de disposición en la que hay dos manivelas con una corredera que actúa como acoplador.
    Algunos ejemplos de mecanismos 3R1P incluyen:
    • Mecanismo de manivela de un solo deslizador (utilizado en motores de combustión interna )
    • Mecanismo de retorno rápido de Whitworth (utilizado en los primeros tipos de moldeadores )
    • Mecanismo de retorno rápido con manivela y palanca ranurada (utilizado en modeladoras)
    • Mecanismo de pistón fijo (utilizado en bombas manuales )
  3. Dos articulaciones revolutas y dos articulaciones prismáticas:
    se denomina PRRP, [2] y se construye conectando dos deslizadores con un enlace acoplador. El deslizador doblador se refiere a todos los arreglos de este tipo.
    Algunos ejemplos de enlaces 2R2P incluyen:

Los eslabones planos de cuatro barras se pueden diseñar para guiar una amplia variedad de movimientos y, a menudo, son los mecanismos básicos que se encuentran en muchas máquinas . Por este motivo, la cinemática y la dinámica de los eslabones planos de cuatro barras también son temas importantes en la ingeniería mecánica .

Vinculación cuadrilátera planar

Los eslabones cuadrilaterales planos, RRRR o 4R, tienen cuatro juntas giratorias. Un eslabón de la cadena suele estar fijo y se denomina eslabón de tierra , eslabón fijo o bastidor . Los dos eslabones conectados al bastidor se denominan eslabones de tierra y, por lo general, son los eslabones de entrada y salida del sistema, a veces denominados eslabón de entrada y eslabón de salida . El último eslabón es el eslabón flotante , que también se denomina acoplador o biela porque conecta una entrada con la salida.

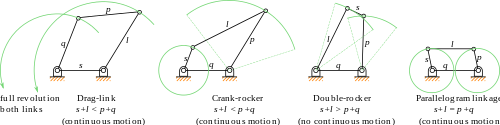
Suponiendo que el marco es horizontal, hay cuatro posibilidades para los enlaces de entrada y salida: [2]

Algunos autores no distinguen entre los tipos de rocker.

Condición de Grashof

La condición de Grashof para un enlace de cuatro barras establece: si la suma del enlace más corto y más largo de un enlace cuadrilátero plano es menor o igual que la suma de los dos enlaces restantes, entonces el enlace más corto puede girar completamente con respecto a un enlace vecino. En otras palabras, la condición se cumple si S + L ≤ P + Q , donde S es el enlace más corto, L es el más largo y P y Q son los otros enlaces.

Clasificación

El movimiento de un eslabón cuadrilátero se puede clasificar en ocho casos en función de las dimensiones de sus cuatro eslabones. Sean a, b, g y h las longitudes de la manivela de entrada, la manivela de salida, el eslabón de tierra y el eslabón flotante, respectivamente. Luego, podemos construir los tres términos:

;
;
.

El movimiento de un enlace cuadrilátero se puede clasificar en ocho tipos según los valores positivos y negativos de estos tres términos, T 1 , T 2 y T 3 . [2]

Los casos de T 1 = 0, T 2 = 0 y T 3 = 0 son interesantes porque los enlaces se pliegan. Si distinguimos el enlace cuadrilátero plegable, entonces hay 27 casos diferentes. [3]

La figura muestra ejemplos de varios casos de vinculación cuadrilátera plana. [4]

Tipos de enlaces de cuatro barras, s : enlace más corto, l : enlace más largo.

La configuración de un enlace cuadrilátero puede clasificarse en tres tipos: convexo, cóncavo y cruzado. En los casos convexo y cóncavo no hay dos enlaces cruzados. En el enlace cruzado dos enlaces se cruzan. En el caso convexo los cuatro ángulos internos son menores de 180 grados, y en la configuración cóncava un ángulo interno es mayor de 180 grados. Existe una relación geométrica simple entre las longitudes de las dos diagonales del cuadrilátero. Para los enlaces convexos y cruzados, la longitud de una diagonal aumenta si y solo si la otra disminuye. Por otro lado, para los enlaces no convexos que no se cruzan, ocurre lo contrario; una diagonal aumenta si y solo si la otra también aumenta. [5]

Diseño de mecanismos de cuatro barras

La síntesis o diseño de mecanismos de cuatro barras es importante cuando se busca producir un movimiento de salida deseado para un movimiento de entrada específico. Para minimizar los costos y maximizar la eficiencia, un diseñador elegirá el mecanismo más simple posible para lograr el movimiento deseado. Al seleccionar un tipo de mecanismo para diseñar, las longitudes de los eslabones deben determinarse mediante un proceso llamado síntesis dimensional. La síntesis dimensional implica una metodología de iteración y análisis que, en ciertas circunstancias, puede ser un proceso ineficiente; sin embargo, en escenarios únicos, es posible que no existan procedimientos exactos y detallados para diseñar un mecanismo preciso. [6]

Relación de tiempo

La relación de tiempo ( Q ) de un mecanismo de cuatro barras es una medida de su retorno rápido y se define de la siguiente manera: [6]

En los mecanismos de cuatro barras hay dos carreras , la de avance y la de retorno, que al sumarse crean un ciclo. Cada carrera puede ser idéntica o tener diferentes velocidades promedio. La relación de tiempo define numéricamente qué tan rápido es la carrera de avance en comparación con la carrera de retorno más rápida. El tiempo de ciclo total ( Δt ciclo ) para un mecanismo es: [6]

La mayoría de los mecanismos de cuatro barras son accionados por un actuador rotatorio, o manivela, que requiere una velocidad constante específica. Esta velocidad requerida ( ω manivela ) está relacionada con el tiempo de ciclo de la siguiente manera: [6]

Algunos mecanismos que producen un movimiento alternativo o repetitivo están diseñados para producir un movimiento simétrico, es decir, el recorrido de avance de la máquina se mueve al mismo ritmo que el recorrido de retorno. Estos mecanismos, a los que se suele denominar diseño en línea , suelen realizar el trabajo en ambas direcciones, ya que ejercen la misma fuerza en ambas direcciones. [6]

Algunos ejemplos de mecanismos de movimiento simétrico incluyen:

Otras aplicaciones requieren que el mecanismo que se va a diseñar tenga una velocidad media más rápida en una dirección que en la otra. Esta categoría de mecanismo es la más deseada para el diseño cuando solo se requiere que el trabajo funcione en una dirección. La velocidad a la que funciona este recorrido único también es muy importante en ciertas aplicaciones de máquinas. En general, el recorrido de retorno y el que no requiere mucho trabajo deben realizarse lo más rápido posible. Esto es así para que la mayor parte del tiempo en cada ciclo se asigne al recorrido que requiere mucho trabajo. Estos mecanismos de retorno rápido suelen denominarse desfasados . [6]

Algunos ejemplos de mecanismos de compensación incluyen:

En el caso de los mecanismos descentrados, es muy importante comprender cómo y en qué medida el descentrado afecta la relación temporal. Para relacionar la geometría de un eslabón específico con la sincronización de la carrera, se utiliza un ángulo de desequilibrio ( β ). Este ángulo está relacionado con la relación temporal, Q , de la siguiente manera: [6]

Mediante un simple reordenamiento algebraico, esta ecuación se puede reescribir para resolver β : [6]

Diagramas de tiempos

Los diagramas de tiempos se utilizan a menudo para sincronizar el movimiento entre dos o más mecanismos. Muestran gráficamente información que muestra dónde y cuándo cada mecanismo está estacionario o realiza sus movimientos de avance y retroceso. Los diagramas de tiempos permiten a los diseñadores describir cualitativamente el comportamiento cinemático requerido de un mecanismo. [6]

Estos gráficos también se utilizan para estimar las velocidades y aceleraciones de ciertos enlaces de cuatro barras. La velocidad de un enlace es la tasa de tiempo en la que cambia su posición, mientras que la aceleración del enlace es la tasa de tiempo en la que cambia su velocidad. Tanto la velocidad como la aceleración son cantidades vectoriales , en el sentido de que tienen magnitud y dirección ; sin embargo, solo se utilizan sus magnitudes en los gráficos de tiempo. Cuando se utilizan con dos mecanismos, los gráficos de tiempo suponen una aceleración constante . Esta suposición produce ecuaciones polinómicas para la velocidad en función del tiempo. La aceleración constante permite que el gráfico de velocidad vs. tiempo aparezca como líneas rectas, designando así una relación entre el desplazamiento ( ΔR ), la velocidad máxima ( v pico ), la aceleración ( a ) y el tiempo ( Δt ). Las siguientes ecuaciones lo muestran. [6] [7]

ΔR = ⁠​1/2⁠ v pico Δ ​​t
ΔR = ⁠​1/4⁠ a (Δ t ) 2

Dados el desplazamiento y el tiempo, se pueden calcular tanto la velocidad máxima como la aceleración de cada mecanismo en un par dado. [6]

Articulación de manivela deslizante

Mecanismos de corredera de manivela con excentricidad 0 y 1,25.

Un mecanismo de corredera-manivela es un mecanismo de cuatro barras con tres juntas giratorias y una junta prismática o deslizante. La rotación de la manivela impulsa el movimiento lineal de la corredera, o la expansión de los gases contra un pistón deslizante en un cilindro puede impulsar la rotación de la manivela.

Hay dos tipos de bielas deslizantes: en línea y desplazadas.

En línea
En una manivela con corredera en línea, la corredera está posicionada de manera que la línea de recorrido de la articulación articulada de la corredera pase por la articulación de la base de la manivela. Esto crea un movimiento simétrico de la corredera hacia adelante y hacia atrás a medida que la manivela gira.
Compensar
Si la línea de recorrido de la articulación articulada del deslizador no pasa por el pivote de la base de la manivela, el movimiento del deslizador no es simétrico. Se mueve más rápido en una dirección que en la otra. Esto se denomina mecanismo de retorno rápido .

Enlaces esféricos y espaciales de cuatro barras

Si el enlace tiene cuatro articulaciones articuladas con ejes en ángulo para intersectarse en un único punto, entonces los enlaces se mueven sobre esferas concéntricas y el conjunto se denomina enlace esférico de cuatro barras . Las ecuaciones de entrada-salida de un enlace esférico de cuatro barras se pueden aplicar a enlaces espaciales de cuatro barras cuando las variables se sustituyen por números duales . [8] Obsérvese que el artículo de conferencia citado confunde incorrectamente las pseudoinversas de Moore-Penrose con las inversas unilaterales de matrices, afirmando falsamente que estas últimas son únicas siempre que existan. Esto se contradice con el hecho de que admite el conjunto de matrices como todas sus inversas izquierdas .

El enlace de Bennett es un enlace espacial de cuatro barras con articulaciones articuladas que tienen sus ejes en un ángulo particular que hace que el sistema sea móvil. [9] [10] [2]

Ejemplos

Otros vínculos y mecanismos

Aplicaciones

Simulaciones

Véase también

Notas

  1. ^ A veces también se denota como 'S' para referirse al deslizador, en lugar de a una junta prismática.
  2. ^ Esto no debe confundirse con el vínculo de movimiento paralelo de Watt .

Referencias

  1. ^ Hartenberg, RS y J. Denavit (1964) Síntesis cinemática de vínculos, Nueva York: McGraw-Hill, enlace en línea de Cornell University .
  2. ^ abcd JM McCarthy y GS Soh, Diseño geométrico de vínculos, 2.ª edición, Springer, 2010
  3. ^ Cvetkovic, Ivana y Stojicevic, Misa y Popkonstantinović, Branislav y Cvetković, Dragan. (2018). Clasificación, análisis geométrico y cinemático de eslabones de cuatro barras. 261-266. 10.15308/Sinteza-2018-261-266.
  4. ^ Diseño de maquinaria 3/e, Robert L. Norton, 2 de mayo de 2003, McGraw Hill. ISBN  0-07-247046-1
  5. ^ Toussaint, Godfried (2003). "Demostraciones simples de una propiedad geométrica de los enlaces de cuatro barras" (PDF) . American Mathematical Monthly . 110 (6): 482–494. doi :10.1080/00029890.2003.11919986. S2CID  16625019.Pruebas adicionales.
  6. ^ abcdefghijk Myszka, David (2012). Máquinas y mecanismos: análisis cinemático aplicado . Nueva Jersey: Pearson Education. ISBN 978-0-13-215780-3.
  7. ^ Chakrabarti, Amaresh (2002). Síntesis de diseño de ingeniería: comprensión, enfoques y herramientas . Gran Bretaña: Springer-Verlag London Limited. ISBN 978-1852334925.
  8. ^ Angeles, Jorge (2012), "Las inversas generalizadas duales y sus aplicaciones en la síntesis cinemática", Últimos avances en cinemática robótica , Springer Netherlands, pp. 1–10, doi :10.1007/978-94-007-4620-6_1, ISBN 9789400746190
  9. ^ Bennett, Geoffrey Thomas (1903). "Un nuevo mecanismo". Ingeniería . 76 (4 de diciembre de 1903): 777–778.
  10. ^ Hunt, KH, Geometría cinemática de mecanismos, Oxford Engineering Science Series, 1979
  11. ^ Phoengsongkhro, S., Tangpornprasert, P., Yotnuengnit, P. et al. Desarrollo de una articulación de rodilla policéntrica de cuatro barras con flexión de rodilla en fase de apoyo. Sci Rep 13, 22809 (2023). https://doi.org/10.1038/s41598-023-49879-4

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Enlace de cuatro barras .