La circunferencia de la Tierra es la distancia que la rodea . Medida alrededor del ecuador , es de 40.075,017 km (24.901,461 mi). Medida pasando por los polos , la circunferencia es de 40.007,863 km (24.859,734 mi). [1]
La medición de la circunferencia de la Tierra ha sido importante para la navegación desde la antigüedad. La primera medición y cálculo científico conocido fue realizado por Eratóstenes , comparando las altitudes del sol del mediodía en dos lugares separados por una distancia norte-sur conocida. [2] Logró un gran grado de precisión en su cálculo. [3] Al tratar la Tierra como una esfera , su circunferencia sería su medida más importante. [4] La Tierra se desvía de la forma esférica en aproximadamente un 0,3%, como se caracteriza por el aplanamiento .
En la época moderna, la circunferencia de la Tierra se ha utilizado para definir unidades fundamentales de medida de longitud: la milla náutica en el siglo XVII y el metro en el XVIII. La circunferencia polar de la Tierra está muy cerca de las 21.600 millas náuticas porque la milla náutica pretendía expresar un minuto de latitud (véase arco meridiano ), que son 21.600 particiones de la circunferencia polar (es decir, 60 minutos × 360 grados). La circunferencia polar también está cerca de los 40.000 kilómetros porque el metro se definió originalmente como una diezmillonésima (es decir, un kilómetro es una diezmilésima) del arco desde el polo hasta el ecuador ( cuarto de meridiano ). La precisión de la medición de la circunferencia ha mejorado desde entonces, pero la longitud física de cada unidad de medida se había mantenido cerca de lo que se determinó que era en ese momento, por lo que la circunferencia de la Tierra ya no es un número redondo en metros o millas náuticas.
La medida de la circunferencia de la Tierra es el más famoso entre los resultados obtenidos por Eratóstenes , [5] quien estimó que el meridiano tiene una longitud de 252.000 estadios , con un error sobre el valor real de entre −2,4% y +0,8% (asumiendo un valor para el estadio entre 155 y 160 metros; [3] el valor exacto del estadio sigue siendo un tema de debate hasta el día de hoy; ver estadio ).
Eratóstenes describió su técnica en un libro titulado Sobre la medida de la Tierra , que no se ha conservado; lo que se ha conservado es la versión simplificada descrita por Cleomedes para popularizar el descubrimiento. [6] Cleomedes invita a su lector a considerar dos ciudades egipcias, Alejandría y Siena (la moderna Asuán ):
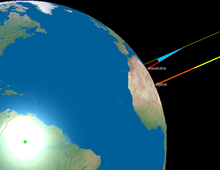
Según el libro De los movimientos circulares de los cuerpos celestes de Cleomedes , alrededor del 240 a. C., Eratóstenes calculó la circunferencia de la Tierra en el Egipto ptolemaico . [8] Utilizando una varilla vertical conocida como gnomon y bajo las suposiciones anteriores, sabía que al mediodía local en el solsticio de verano en Siena (la moderna Asuán , Egipto), el Sol estaba directamente sobre su cabeza, ya que el gnomon no proyectaba sombra. Además, la sombra de alguien que miraba hacia un pozo profundo en ese momento en Siena bloqueaba el reflejo del Sol en el agua. Eratóstenes luego midió el ángulo de elevación del Sol al mediodía en Alejandría midiendo la longitud de la sombra de otro gnomon en el suelo. [9] Usando la longitud de la varilla y la longitud de la sombra como los catetos de un triángulo, calculó el ángulo de los rayos del sol. [10] Este ángulo era de aproximadamente 7°, o 1/50 de la circunferencia de un círculo ; Suponiendo que la Tierra es perfectamente esférica, concluyó que su circunferencia era 50 veces la distancia conocida de Alejandría a Siena (5.000 estadios, una cifra que se comprobaba anualmente), es decir, 250.000 estadios . [11] Dependiendo de si utilizaba el "estadio olímpico" (176,4 m) o el estadio italiano (184,8 m), esto implicaría una circunferencia de 44.100 km (un error del 10%) o 46.100 km, un error del 15%. [11] LV Firsov incluso ha postulado un valor para el estadio de 157,7 metros, que daría una precisión aún mejor, pero está plagado de errores de cálculo y suposiciones falsas. [12] En 2012, Anthony Abreu Mora repitió el cálculo de Eratóstenes con datos más precisos; El resultado fue 40.074 km, lo que supone una diferencia de 66 km (0,16%) con respecto a la circunferencia polar actualmente aceptada. [10]

El método de Eratóstenes era en realidad más complicado, como lo afirma el mismo Cleomedes, cuyo propósito era presentar una versión simplificada del descrito en el libro de Eratóstenes. Plinio, por ejemplo, ha citado un valor de 252.000 estadios. [13]
El método se basaba en varios viajes de reconocimiento realizados por bematistas profesionales , cuyo trabajo era medir con precisión la extensión del territorio de Egipto con fines agrícolas y tributarios. [3] Además, el hecho de que la medida de Eratóstenes corresponda exactamente a 252.000 estadios (según Plinio) podría ser intencional, ya que es un número que se puede dividir por todos los números naturales del 1 al 10: algunos historiadores creen que Eratóstenes cambió el valor de 250.000 escrito por Cleomedes a este nuevo valor para simplificar los cálculos; [14] otros historiadores de la ciencia, por otro lado, creen que Eratóstenes introdujo una nueva unidad de longitud basada en la longitud del meridiano, como afirma Plinio, que escribe sobre el estadio "según la razón de Eratóstenes". [3] [13]
Posidonio calculó la circunferencia de la Tierra en función de la posición de la estrella Canopo . Como explicó Cleomedes , Posidonio observó a Canopo en el horizonte de Rodas , pero nunca por encima de él , mientras que en Alejandría la vio ascender hasta 7+1 ⁄ 2 grados sobre el horizonte (el arco meridiano entre la latitud de los dos lugares es en realidad 5 grados 14 minutos). Como pensaba que Rodas estaba a 5.000 estadios al norte de Alejandría, y la diferencia en la elevación de la estrella indicaba que la distancia entre los dos lugares era 1/48 del círculo, multiplicó 5.000 por 48 para llegar a una cifra de 240.000 estadios para la circunferencia de la Tierra. [15] Se cree generalmente [ ¿ por quién? ] que el estadio utilizado por Posidonio era casi exactamente 1/10 de una milla estatutaria moderna. [ cita requerida ] Por lo tanto, la medida de Posidonio de 240.000 estadios se traduce en 24.000 mi (39.000 km), no mucho menos que la circunferencia real de 24.901 mi (40.074 km). [15] Estrabón señaló que la distancia entre Rodas y Alejandría es de 3750 estadios, y reportó que la estimación de Posidonio de la circunferencia de la Tierra era de 180 000 estadios o 18 000 mi (29 000 km). [16] Plinio el Viejo menciona a Posidonio entre sus fuentes y, sin nombrarlo, informó su método para estimar la circunferencia de la Tierra. No obstante, señaló que Hiparco había agregado unos 26 000 estadios a la estimación de Eratóstenes. El valor más pequeño ofrecido por Estrabón y las diferentes longitudes de los estadios griegos y romanos han creado una confusión persistente en torno al resultado de Posidonio. Ptolomeo usó el valor más bajo de Posidonio de 180 000 estadios (aproximadamente un 33 % demasiado bajo) para la circunferencia de la Tierra en su Geografía . Este fue el número usado por Cristóbal Colón para subestimar la distancia a la India en 70 000 estadios. [17]
Alrededor del año 525 d. C., el matemático y astrónomo indio Aryabhata escribió Aryabhatiya , en el que calculó que el diámetro de la Tierra era de 1.050 yojanas . La longitud de la yojana prevista por Aryabhata es objeto de controversia. Una lectura cuidadosa da un equivalente de 14.200 kilómetros (8.800 mi), demasiado grande en un 11 %. [18] Otra da 15.360 km (9.540 mi), demasiado grande en un 20 %. [19] Y otra da 13.440 km (8.350 mi), demasiado grande en un 5 %. [20]
Alrededor del año 830 d. C., el califa Al-Ma'mun encargó a un grupo de astrónomos musulmanes dirigidos por Al-Khwarizmi que midieran la distancia entre Tadmur ( Palmira ) y Raqqa , en la actual Siria . Calcularon que la circunferencia de la Tierra se aproximaba en un 15% al valor actual, y posiblemente mucho más. No se sabe con certeza hasta qué punto era exacta debido a la incertidumbre en la conversión entre las unidades árabes medievales y las unidades modernas, pero en cualquier caso, las limitaciones técnicas de los métodos y las herramientas no permitían una precisión mejor que el 5% aproximadamente. [21]

En el Codex Masudicus (1037) de Al-Biruni se proporcionaba una forma más cómoda de realizar la estimación . A diferencia de sus predecesores, que medían la circunferencia de la Tierra observando el Sol simultáneamente desde dos lugares, Al-Biruni desarrolló un nuevo método de utilizar cálculos trigonométricos , basado en el ángulo entre una llanura y la cima de una montaña , lo que hizo posible que una sola persona pudiera medirlo desde un único lugar. [21] Desde la cima de la montaña, observó el ángulo de inclinación que, junto con la altura de la montaña (que determinó de antemano), aplicó a la fórmula de la ley de los senos . Este fue el primer uso conocido del ángulo de inclinación y el primer uso práctico de la ley de los senos. [22] Sin embargo, el método no podía proporcionar resultados más precisos que los métodos anteriores, debido a limitaciones técnicas, por lo que Al-Biruni aceptó el valor calculado el siglo anterior por la expedición de Al-Ma'mun . [21]
1.700 años después de la muerte de Eratóstenes, Cristóbal Colón estudió lo que éste había escrito sobre el tamaño de la Tierra. Sin embargo, basándose en un mapa de Toscanelli , optó por creer que la circunferencia de la Tierra era un 25% menor. Si, en cambio, Colón hubiera aceptado el valor mayor de Eratóstenes, habría sabido que el lugar donde tocó tierra no era Asia , sino un Nuevo Mundo . [23]
En 1617, el científico holandés Willebrord Snellius calculó la circunferencia de la Tierra en 24.630 millas romanas (24.024 millas terrestres). En esa época, el matemático británico Edmund Gunter mejoró las herramientas de navegación, incluido un nuevo cuadrante para determinar la latitud en el mar. Razonó que las líneas de latitud podrían usarse como base para una unidad de medida de distancia y propuso la milla náutica como un minuto o un sexagésimo ( 1/60) de un grado de latitud. Como un grado es 1/360 de un círculo, un minuto de arco es 1/21600 de un círculo, de modo que la circunferencia polar de la Tierra sería exactamente 21.600 millas. Gunter utilizó la circunferencia de Snellius para definir una milla náutica como 6.080 pies, la longitud de un minuto de arco a 48 grados de latitud. [24]
En 1793, Francia definió el metro de manera que la circunferencia polar de la Tierra fuera de 40.000 kilómetros. Para medir esta distancia con precisión, la Academia Francesa de Ciencias encargó a Jean Baptiste Joseph Delambre y Pierre Méchain que lideraran una expedición para intentar medir con precisión la distancia entre un campanario de Dunkerque y el castillo de Montjuïc en Barcelona para estimar la longitud del arco meridiano que pasa por Dunkerque. La longitud del primer prototipo de barra de metro se basó en estas mediciones, pero más tarde se determinó que su longitud era aproximadamente 0,2 milímetros menor debido a un error de cálculo del aplanamiento de la Tierra, lo que hizo que el prototipo fuera aproximadamente un 0,02% más corto que la definición original propuesta del metro. A pesar de todo, esta longitud se convirtió en el estándar francés y fue adoptada progresivamente por otros países de Europa. [25] Es por eso que la circunferencia polar de la Tierra es en realidad de 40.008 kilómetros, en lugar de 40.000.