problema de cumpleaños

Probabilidad de cumpleaños compartidos

La probabilidad calculada de que al menos dos personas compartan un cumpleaños versus el número de personas

En la teoría de la probabilidad , el problema del cumpleaños pregunta por la probabilidad de que, en un conjunto de n personas elegidas al azar , al menos dos compartan un cumpleaños . La paradoja del cumpleaños se refiere al hecho contraintuitivo de que sólo se necesitan 23 personas para que esa probabilidad supere el 50%.

La paradoja del cumpleaños es una paradoja verídica : parece errónea a primera vista pero, de hecho, es cierta. Si bien puede parecer sorprendente que sólo se requieran 23 personas para alcanzar una probabilidad del 50% de tener un cumpleaños compartido, este resultado se vuelve más intuitivo al considerar que las comparaciones de cumpleaños se harán entre cada par posible de individuos. Con 23 personas, hay ⁠23 × 22/2⁠  = 253 pares a considerar, mucho más de la mitad de los días de un año.

Las aplicaciones del mundo real para el problema del cumpleaños incluyen un ataque criptográfico llamado ataque de cumpleaños , que utiliza este modelo probabilístico para reducir la complejidad de encontrar una colisión para una función hash , así como para calcular el riesgo aproximado de una colisión hash existente dentro de los hashes. de un determinado tamaño de población.

El problema se atribuye generalmente a Harold Davenport alrededor de 1927, aunque no lo publicó en ese momento. Davenport no afirmó ser su descubridor "porque no podía creer que no se hubiera dicho antes". ^{[1] [2]} La primera publicación de una versión del problema del cumpleaños fue de Richard von Mises en 1939. ^[3]

Calculando la probabilidad

Desde una perspectiva de permutaciones , sea el evento A la probabilidad de encontrar un grupo de 23 personas sin cumpleaños repetidos. Donde el evento B es la probabilidad de encontrar un grupo de 23 personas con al menos dos personas que comparten el mismo cumpleaños, P ( B ) = 1 − P ( A ) . P ( A ) es la relación entre el número total de cumpleaños, sin repeticiones ni cuestiones de orden (por ejemplo, para un grupo de 2 personas, formato de cumpleaños mm/dd, un resultado posible es ) dividido por el número total de cumpleaños con repetición y El orden importa, ya que es el espacio total de resultados del experimento (por ejemplo, 2 personas, un resultado posible es ). Por lo tanto y son permutaciones . ${\displaystyle V_{nr}}$ ${\displaystyle \left\{\left\{01/02,05/20\right\},\left\{05/20,01/02\right\},\left\{10/02,08/04\right\},...\right\}}$ ${\displaystyle V_{t}}$ ${\displaystyle \left\{\left\{01/02,01/02\right\},\left\{10/02,08/04\right\},...\right\}}$ ${\displaystyle V_{nr}}$ ${\displaystyle V_{t}}$

${\displaystyle {\begin{aligned}V_{nr}&={\frac {n!}{(n-k)!}}={\frac {365!}{(365-23)!}}\\[8pt]V_{t}&=n^{k}=365^{23}\\[8pt]P(A)&={\frac {V_{nr}}{V_{t}}}\approx 0.492703\\[8pt]P(B)&=1-P(A)\approx 1-0.492703\approx 0.507297\quad (50.7297\%)\end{aligned}}}$

Otra forma de resolver el problema del cumpleaños es preguntando una probabilidad aproximada de que en un grupo de n personas al menos dos tengan el mismo cumpleaños. Para simplificar, los años bisiestos , los gemelos , el sesgo de selección y las variaciones estacionales y semanales en las tasas de natalidad ^[4] generalmente no se tienen en cuenta y, en su lugar, se supone que hay 365 cumpleaños posibles y que es igualmente probable que el cumpleaños de cada persona sea cualquiera de estos días, independiente de las demás personas del grupo.

Para cumpleaños independientes, una distribución uniforme de cumpleaños minimiza la probabilidad de que dos personas de un grupo tengan el mismo cumpleaños. Cualquier desnivel aumenta la probabilidad de que dos personas compartan el cumpleaños. ^{[5] [6]} Sin embargo, los cumpleaños en el mundo real no son lo suficientemente desiguales como para generar muchos cambios: el tamaño del grupo en el mundo real necesario para tener una probabilidad superior al 50% de tener un cumpleaños compartido es 23, como en la distribución uniforme teórica. ^[7]

El objetivo es calcular P ( B ) , la probabilidad de que al menos dos personas en la habitación tengan el mismo cumpleaños. Sin embargo, es más sencillo calcular P ( A ′) , la probabilidad de que no haya dos personas en la habitación que tengan el mismo cumpleaños. Entonces, debido a que B y A ′ son las dos únicas posibilidades y también son mutuamente excluyentes , P ( B ) = 1 − P ( A ′).

Aquí está el cálculo de P ( B ) para 23 personas. Supongamos que las 23 personas se numeran del 1 al 23. El evento de que las 23 personas tengan cumpleaños diferentes es el mismo que el evento de que la persona 2 no tenga el mismo cumpleaños que la persona 1 y que la persona 3 no tenga el mismo cumpleaños que ninguna de las dos. persona 1 o persona 2, y así sucesivamente, y finalmente esa persona 23 no tiene el mismo cumpleaños que ninguna de las personas 1 a 22. Llamémonos estos eventos Evento 2, Evento 3, y así sucesivamente. El evento 1 es el evento en el que la persona 1 cumple años, lo que ocurre con probabilidad 1. Esta conjunción de eventos se puede calcular usando probabilidad condicional : la probabilidad del evento 2 es ⁠364/365⁠ , ya que la persona 2 puede tener cualquier cumpleaños distinto del cumpleaños de la persona 1. De manera similar, la probabilidad del Evento 3 dado que ocurrió el Evento 2 es ⁠363/365⁠ , ya que la persona 3 puede tener cualquiera de los cumpleaños que aún no hayan cumplido las personas 1 y 2. Esto continúa hasta que finalmente la probabilidad del Evento 23 dado que ocurrieron todos los eventos anteriores es ⁠343/365⁠ . Finalmente, el principio de probabilidad condicional implica que P ( A ′) es igual al producto de estas probabilidades individuales:

Los términos de la ecuación ( 1 ) se pueden recopilar para llegar a:

La evaluación de la ecuación ( 2 ) da P ( A ′) ≈ 0,492703

Por lo tanto, P ( B ) ≈ 1 − 0,492703 = 0,507297  (50,7297%).

Este proceso se puede generalizar a un grupo de n personas, donde p ( n ) es la probabilidad de que al menos dos de las n personas coincidan en su cumpleaños. Es más fácil calcular primero la probabilidad p ( n ) de que los n cumpleaños sean diferentes . Según el principio del casillero , p ( n ) es cero cuando n > 365 . Cuando n  ≤ 365 :

${\displaystyle {\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \left(1-{\frac {2}{365}}\right)\times \cdots \times \left(1-{\frac {n-1}{365}}\right)\\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}}\\[6pt]&={\frac {365!}{365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}}{365^{n}}}={\frac {_{365}P_{n}}{365^{n}}}\end{aligned}}}$

dónde ! es el operador factorial , (³⁶⁵
_norte) es el coeficiente binomial y _k P _r denota permutación .

La ecuación expresa el hecho de que la primera persona no tiene con quién compartir cumpleaños, la segunda persona no puede tener el mismo cumpleaños que la primera ( ⁠364/365⁠ ) , el tercero no puede tener el mismo cumpleaños que ninguno de los dos primeros ( ⁠363/365⁠ ) ​​y, en general, elenésimocumpleaños no puede ser el mismo que cualquiera de los n − 1cumpleaños anteriores.

El evento de que al menos dos de las n personas tengan el mismo cumpleaños es complementario a que todos los n cumpleaños sean diferentes. Por lo tanto, su probabilidad p ( n ) es

${\displaystyle p(n)=1-{\bar {p}}(n).}$

La siguiente tabla muestra la probabilidad de algunos otros valores de n (para esta tabla, se ignora la existencia de años bisiestos y se supone que cada cumpleaños es igualmente probable):

La probabilidad de que no haya dos personas que compartan el mismo cumpleaños en un grupo de n personas. Tenga en cuenta que la escala vertical es logarítmica (cada paso hacia abajo es 10 ²⁰ veces menos probable).

Aproximaciones

Gráficos que muestran las probabilidades aproximadas de que al menos dos personas compartan un cumpleaños ( rojo ) y su evento complementario ( azul )

Un gráfico que muestra la precisión de la aproximación 1 − e ^{− n 2 /730} ( rojo )

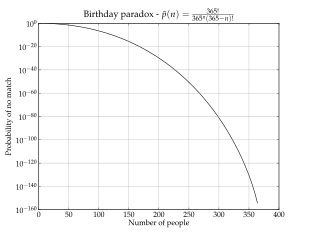
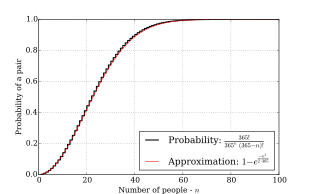
La expansión en serie de Taylor de la función exponencial (la constante e ≈2.718 281 828 )

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots }$

proporciona una aproximación de primer orden para e ^x para : ${\displaystyle |x|\ll 1}$

${\displaystyle e^{x}\approx 1+x.}$

Para aplicar esta aproximación a la primera expresión derivada para p ( n ) , establezca x = − ⁠a/365⁠ . De este modo,

${\displaystyle e^{-a/365}\approx 1-{\frac {a}{365}}.}$

Luego, reemplaza a con números enteros no negativos para cada término en la fórmula de p ( n ) hasta que a = n − 1 , por ejemplo, cuando a = 1 ,

${\displaystyle e^{-1/365}\approx 1-{\frac {1}{365}}.}$

La primera expresión derivada para p ( n ) se puede aproximar como

${\displaystyle {\begin{aligned}{\bar {p}}(n)&\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}\\[6pt]&=e^{-{\big (}1+2+\,\cdots \,+(n-1){\big )}/365}\\[6pt]&=e^{-{\frac {n(n-1)/2}{365}}}=e^{-{\frac {n(n-1)}{730}}}.\end{aligned}}}$

Por lo tanto,

${\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-{\frac {n(n-1)}{730}}}.}$

Una aproximación aún más aproximada está dada por

${\displaystyle p(n)\approx 1-e^{-{\frac {n^{2}}{730}}},}$

lo cual, como ilustra el gráfico, sigue siendo bastante preciso.

Según la aproximación, el mismo enfoque se puede aplicar a cualquier número de "personas" y "días". Si en lugar de 365 días hay d , si hay n personas y si n ≪ d , entonces usando el mismo enfoque anterior logramos el resultado de que si p ( n , d ) es la probabilidad de que al menos dos de n las personas comparten el mismo cumpleaños de un conjunto de d días disponibles, entonces:

${\displaystyle {\begin{aligned}p(n,d)&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\[6pt]&\approx 1-e^{-{\frac {n^{2}}{2d}}}.\end{aligned}}}$

exponenciación simple

La probabilidad de que dos personas cualesquiera no tengan el mismo cumpleaños es ⁠364/365⁠ . En una habitación que contiene n personas, hay (^norte
₂) = ⁠norte ( norte - 1)/2⁠ pares de personas, es decir (^norte
₂) eventos. La probabilidad de que dos personas no compartan el mismo cumpleaños se puede aproximar suponiendo que estos eventos son independientes y, por lo tanto, multiplicando su probabilidad. Ser independiente equivaldría a escoger con reemplazo , cualquier par de personas en el mundo, no sólo en una habitación. En resumen ⁠364/365⁠ se puede multiplicar por sí mismo (^norte
₂) veces, lo que nos da

${\displaystyle {\bar {p}}(n)\approx \left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Dado que esta es la probabilidad de que nadie tenga el mismo cumpleaños, entonces la probabilidad de que alguien comparta el mismo cumpleaños es

${\displaystyle p(n)\approx 1-\left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Y para el grupo de 23 personas, la probabilidad de compartir es

${\displaystyle p(23)\approx 1-\left({\frac {364}{365}}\right)^{\binom {23}{2}}=1-\left({\frac {364}{365}}\right)^{253}\approx 0.500477.}$

Aproximación de Poisson

Aplicando la aproximación de Poisson para el binomio al grupo de 23 personas,

${\displaystyle \operatorname {Poi} \left({\frac {\binom {23}{2}}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0.6932)}$

entonces

${\displaystyle \Pr(X>0)=1-\Pr(X=0)\approx 1-e^{-0.6932}\approx 1-0.499998=0.500002.}$

El resultado es superior al 50% de las descripciones anteriores. Esta aproximación es la misma que la anterior basada en la expansión de Taylor que usa e ^x ≈ 1 + x .

Aproximación cuadrada

Una buena regla general que se puede utilizar para el cálculo mental es la relación

${\displaystyle p(n,d)\approx {\frac {n^{2}}{2d}}}$

que también se puede escribir como

${\displaystyle n\approx {\sqrt {2d\times p(n)}}}$

que funciona bien para probabilidades menores o iguales a ⁠1/2⁠ . En estas ecuaciones, d es el número de días de un año.

Por ejemplo, para estimar la cantidad de personas necesarias para un ⁠1/2⁠ posibilidad de un cumpleaños compartido, tenemos

${\displaystyle n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}}\approx 19}$

Lo cual no está muy lejos de la respuesta correcta de 23.

Aproximación del número de personas.

Esto también se puede aproximar usando la siguiente fórmula para la cantidad de personas necesarias para tener al menos un ⁠1/2⁠ posibilidades de coincidencia:

${\displaystyle n\geq {\tfrac {1}{2}}+{\sqrt {{\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.999943.}$

Esto es el resultado de la buena aproximación que tiene un evento con ⁠1/k⁠ probabilidad tendrá un ⁠1/2⁠ probabilidad de ocurrir al menos una vez si se repite k ln 2 veces. ^[8]

tabla de probabilidad

Comparación del problema de cumpleaños (1) y el ataque de cumpleaños (2):

En (1), las colisiones se encuentran dentro de un conjunto, en este caso, 3 de 276 parejas de 24 astronautas lunares.

En (2), se encuentran colisiones entre dos conjuntos, en este caso, 1 de 256 pares de solo los primeros bytes de hashes SHA-256 de 16 variantes cada uno de contratos benignos y dañinos.

Los campos más claros de esta tabla muestran la cantidad de hashes necesarios para lograr la probabilidad de colisión dada (columna) dado un espacio hash de cierto tamaño en bits (fila). Usando la analogía del cumpleaños: el "tamaño del espacio hash" se parece a los "días disponibles", la "probabilidad de colisión" se parece a la "probabilidad de cumpleaños compartido" y el "número requerido de elementos hash" se parece al "número requerido de personas en Un grupo". También se podría utilizar este gráfico para determinar el tamaño mínimo de hash requerido (dados los límites superiores de los hashes y la probabilidad de error), o la probabilidad de colisión (para un número fijo de hashes y la probabilidad de error).

Para comparacion,10 ⁻¹⁸ a10 ⁻¹⁵ es la tasa de error de bits incorregible de un disco duro típico. ^[9] En teoría, las funciones hash de 128 bits, como MD5 , deberían permanecer dentro de ese rango hasta aproximadamente8,2 × 10 ¹¹ documentos, aunque sus posibles salidas son muchas más.

Un límite superior para la probabilidad y un límite inferior para el número de personas

El siguiente argumento está adaptado de un argumento de Paul Halmos . ^{[nota 1]}

Como se indicó anteriormente, la probabilidad de que no coincidan dos cumpleaños es

${\displaystyle 1-p(n)={\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).}$

Como en párrafos anteriores, el interés reside en el n más pequeño tal que p ( n ) > ⁠1/2⁠ ; o equivalentemente, el n más pequeño tal que p ( n ) < ⁠1/2⁠ .

Usando la desigualdad 1 − x < e ^{− x} en la expresión anterior reemplazamos 1 − ⁠k/365⁠ con mi ^{− k ⁄ 365} . Esto produce

${\displaystyle {\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-{\frac {k}{365}}}\right)=e^{-{\frac {n(n-1)}{730}}}.}$

Por lo tanto, la expresión anterior no es sólo una aproximación, sino también un límite superior de p ( n ) . La desigualdad

${\displaystyle e^{-{\frac {n(n-1)}{730}}}<{\frac {1}{2}}}$

implica p ( n ) < ⁠1/2⁠ . Resolver para n da

${\displaystyle n^{2}-n>730\ln 2.}$

Ahora, 730 ln 2 es aproximadamente 505,997, que está apenas por debajo de 506, el valor de n ² − n alcanzado cuando n = 23 . Por tanto, 23 personas son suficientes. Por cierto, resolver n ² − n = 730 ln 2 para n da la fórmula aproximada de Frank H. Mathis citado anteriormente.

Esta derivación sólo muestra que se necesitan como máximo 23 personas para garantizar que las posibilidades de una coincidencia de cumpleaños sean al menos iguales; deja abierta la posibilidad de que n sea 22 o menos también podría funcionar.

Generalizaciones

Número arbitrario de días.

Dado un año con d días, el problema de cumpleaños generalizado solicita el número mínimo n ( d ) tal que, en un conjunto de n personas elegidas al azar, la probabilidad de que el cumpleaños coincida sea al menos del 50%. En otras palabras, n ( d ) es el entero mínimo n tal que

${\displaystyle 1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots \left(1-{\frac {n-1}{d}}\right)\geq {\frac {1}{2}}.}$

El problema clásico del cumpleaños corresponde, por tanto, a determinar n (365) . Los primeros 99 valores de n ( d ) se dan aquí (secuencia A033810 en OEIS ):

Un cálculo similar muestra que n ( d ) = 23 cuando d está en el rango 341–372.

Se han publicado varios límites y fórmulas para n ( d ) . ^[10] Para cualquier d ≥ 1 , el número n ( d ) satisface ^[11]

${\displaystyle {\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}.}$

Estos límites son óptimos en el sentido de que la secuencia n ( d ) − √ 2 d ln 2 se acerca arbitrariamente a

${\displaystyle {\frac {3-2\ln 2}{6}}\approx 0.27,}$

mientras tiene

${\displaystyle 9-{\sqrt {86\ln 2}}\approx 1.28}$

como máximo, tomado para d = 43 .

Los límites son lo suficientemente ajustados como para dar el valor exacto de n ( d ) en la mayoría de los casos. Por ejemplo, para d = 365 estos límites implican que 22,7633 < n (365) < 23,7736 y 23 es el único número entero en ese rango. En general, de estos límites se deduce que n ( d ) siempre es igual a

${\displaystyle \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{or}}\quad \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil +1}$

donde ⌈·⌉ denota la función techo . La formula

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil }$

se cumple para el 73% de todos los números enteros d . ^[12] La fórmula

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}\right\rceil }$

es válido para casi todos los d , es decir, para un conjunto de números enteros d con densidad asintótica 1. ^[12]

La formula

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}\right\rceil }$

es válido para todo d ≤10, ¹⁸ , pero se conjetura que hay infinitos contraejemplos de esta fórmula. ^[13]

La formula

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}-{\frac {2(\ln 2)^{2}}{135d}}\right\rceil }$

es válido para todo d ≤10 ¹⁸ , y se conjetura que esta fórmula es válida para todo d . ^[13]

Más de dos personas compartiendo un cumpleaños

Es posible ampliar el problema para preguntar cuántas personas en un grupo son necesarias para que haya una probabilidad superior al 50% de que al menos 3, 4, 5, etc. del grupo compartan el mismo cumpleaños.

Los primeros valores son los siguientes: >50 % de probabilidad de que 3 personas compartan el mismo cumpleaños: 88 personas; >50% de probabilidad de que 4 personas compartan un cumpleaños - 187 personas (secuencia A014088 en la OEIS ). ^[14]

Probabilidad de un cumpleaños compartido (colisión)

El problema del cumpleaños se puede generalizar de la siguiente manera:

Dados n enteros aleatorios extraídos de una distribución uniforme discreta con rango [1, d ] , ¿cuál es la probabilidad p ( n ; d ) de que al menos dos números sean iguales? ( d = 365 da el problema habitual de cumpleaños). ^[15]

Los resultados genéricos se pueden derivar utilizando los mismos argumentos dados anteriormente.

${\displaystyle {\begin{aligned}p(n;d)&={\begin{cases}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}}\right)&n\leq d\\1&n>d\end{cases}}\\[8px]&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\&\approx 1-\left({\frac {d-1}{d}}\right)^{\frac {n(n-1)}{2}}\end{aligned}}}$

Por el contrario, si n ( p ; d ) denota el número de enteros aleatorios extraídos de [1, d ] para obtener una probabilidad p de que al menos dos números sean iguales, entonces

${\displaystyle n(p;d)\approx {\sqrt {2d\cdot \ln \left({\frac {1}{1-p}}\right)}}.}$

El problema del cumpleaños en este sentido más genérico se aplica a las funciones hash : el número esperado de hashes de N bits que pueden generarse antes de producirse una colisión no es 2 N ^, sino sólo 2 ^{N ⁄ 2} . Esto se aprovecha mediante ataques de cumpleaños a funciones hash criptográficas y es la razón por la que un pequeño número de colisiones en una tabla hash son, a todos los efectos prácticos, inevitables.

La teoría detrás del problema del cumpleaños fue utilizada por Zoe Schnabel ^[16] bajo el nombre de estadística de captura-recaptura para estimar el tamaño de la población de peces en los lagos.

Generalización a múltiples tipos de personas.

Gráfica de la probabilidad de que al menos un hombre y una mujer compartan al menos un cumpleaños

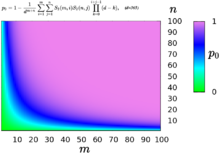
El problema básico considera que todos los ensayos son de un "tipo". El problema del cumpleaños se ha generalizado para considerar un número arbitrario de tipos. ^[17] En la extensión más simple, hay dos tipos de personas, digamos m hombres yn mujeres, y el problema consiste en caracterizar la probabilidad de un cumpleaños compartido entre al menos un hombre y una mujer. (Los cumpleaños compartidos entre dos hombres o dos mujeres no cuentan). La probabilidad de que no haya cumpleaños compartidos aquí es

${\displaystyle p_{0}={\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k}$

donde d = 365 y S ₂ son números de Stirling de segunda especie . En consecuencia, la probabilidad deseada es 1 − p ₀ .

Esta variación del problema del cumpleaños es interesante porque no existe una solución única para el número total de personas m + n . Por ejemplo, el valor de probabilidad habitual del 50% se obtiene tanto para un grupo de 32 miembros de 16 hombres y 16 mujeres como para un grupo de 49 miembros de 43 mujeres y 6 hombres.

Otros problemas de cumpleaños

Primer partido

Una pregunta relacionada es: cuando las personas entran a una habitación de una en una, ¿cuál tiene más probabilidades de ser la primera en tener el mismo cumpleaños que alguien que ya está en la habitación? Es decir, ¿para qué n es p ( n ) − p ( n  − 1) máximo? La respuesta es 20: si hay premio para el primer partido, la mejor posición en la fila es la 20.ª. ^{[ cita necesaria ]}

El mismo cumpleaños que tú.

Comparando p ( n ) = probabilidad de coincidir con su cumpleaños con q ( n ) = probabilidad de coincidir con su cumpleaños

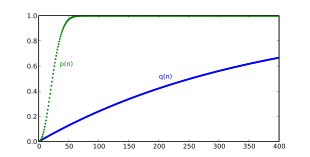
En el problema del cumpleaños, ninguna de las dos personas es elegida de antemano. Por el contrario, la probabilidad q ( n ) de que al menos otra persona en una habitación con n personas tenga el mismo cumpleaños que una persona en particular (por ejemplo, usted) está dada por

${\displaystyle q(n)=1-\left({\frac {365-1}{365}}\right)^{n}}$

y para general d por

${\displaystyle q(n;d)=1-\left({\frac {d-1}{d}}\right)^{n}.}$

En el caso estándar de d = 365 , sustituir n = 23 da aproximadamente un 6,1%, lo que es menos de 1 probabilidad entre 16. Para una probabilidad superior al 50% de que al menos otra persona en una habitación llena de n personas tenga el mismo cumpleaños como usted , n tendría que ser al menos 253. Este número es significativamente mayor que ⁠365/2⁠ = 182,5 : la razón es que es probable que haya algunas coincidencias de cumpleaños entre las demás personas en la sala.

Número de personas con un cumpleaños compartido

Para cualquier persona en un grupo de n personas, la probabilidad de que comparta su cumpleaños con otra persona es , como se explicó anteriormente. El número esperado de personas con un cumpleaños compartido (no único) ahora se puede calcular fácilmente multiplicando esa probabilidad por el número de personas ( n ), por lo que es: ${\displaystyle q(n-1;d)}$

${\displaystyle n\left(1-\left({\frac {d-1}{d}}\right)^{n-1}\right)}$

(Esta multiplicación se puede realizar de esta manera debido a la linealidad del valor esperado de las variables indicadoras). Esto implica que el número esperado de personas con una fecha de nacimiento no compartida (única) es:

${\displaystyle n\left({\frac {d-1}{d}}\right)^{n-1}}$

Se pueden derivar fórmulas similares para el número esperado de personas que comparten con otras tres, cuatro, etc.

Número de personas hasta cumplir cada cumpleaños

El número esperado de personas necesarias hasta que se cumpla cada cumpleaños se denomina problema del coleccionista de cupones . Puede calcularse mediante nH _n , donde H _n es el enésimo número armónico . Para 365 fechas posibles (el problema del cumpleaños), la respuesta es 2365.

Cerca de partidos

Otra generalización es preguntar la probabilidad de encontrar al menos un par en un grupo de n personas con cumpleaños dentro de k días calendario entre sí, si hay d cumpleaños igualmente probables. ^[18]

${\displaystyle {\begin{aligned}p(n,k,d)&=1-{\frac {(d-nk-1)!}{d^{n-1}{\bigl (}d-n(k+1){\bigr )}!}}\end{aligned}}}$

El número de personas necesarias para que la probabilidad de que alguna pareja cumpla años separados por k días o menos sea superior al 50% se da en la siguiente tabla:

Por lo tanto, en un grupo de sólo siete personas al azar, lo más probable es que dos de ellas cumplan años con una semana de diferencia. ^[18]

Número de días con una determinada cantidad de cumpleaños.

Número de días con al menos un cumpleaños

El número esperado de cumpleaños diferentes, es decir, el número de días en los que al menos una persona cumple años, es:

${\displaystyle d-d\left({\frac {d-1}{d}}\right)^{n}}$

Esto se desprende del número esperado de días en los que nadie cumple años:

${\displaystyle d\left({\frac {d-1}{d}}\right)^{n}}$

que se sigue de la probabilidad de que un día determinado no sea el cumpleaños de nadie, ( ⁠re - 1/d⁠ )^norte
 , se suma fácilmente debido a la linealidad del valor esperado.

Por ejemplo, con d = 365 , deberías esperar alrededor de 21 cumpleaños diferentes cuando hay 22 personas, o 46 cumpleaños diferentes cuando hay 50 personas. Cuando hay 1000 personas, habrá alrededor de 341 cumpleaños diferentes (24 cumpleaños no reclamados).

Número de días con al menos dos cumpleaños

Lo anterior se puede generalizar a partir de la distribución del número de personas que cumplen años en un día en particular, que es una distribución binomial con probabilidad ⁠1/d⁠ . Multiplicar la probabilidad relevante por d dará el número esperado de días. Por ejemplo, la cantidad esperada de días que se comparten; es decir, cuál es el cumpleaños de al menos dos (es decir, no cero ni uno) personas es:

$${\displaystyle d-d\left({\frac {d-1}{d}}\right)^{n}-d\cdot {\binom {n}{1}}\left({\frac {1}{d}}\right)^{1}\left({\frac {d-1}{d}}\right)^{n-1}=d-d\left({\frac {d-1}{d}}\right)^{n}-n\left({\frac {d-1}{d}}\right)^{n-1}}$$

Número de personas que repiten cumpleaños

La probabilidad de que el k -ésimo entero elegido aleatoriamente entre [1, d ] repita al menos una elección anterior es igual a q ( k − 1; d ) anterior. El número total esperado de veces que una selección repetirá una selección anterior cuando se eligen n números enteros iguales a ^[19]

${\displaystyle \sum _{k=1}^{n}q(k-1;d)=n-d+d\left({\frac {d-1}{d}}\right)^{n}}$

Se puede ver que esto es igual al número de personas menos el número esperado de cumpleaños diferentes.

Número promedio de personas que tienen al menos un cumpleaños compartido

En una formulación alternativa del problema del cumpleaños, se pregunta cuál es el número promedio de personas necesarias para encontrar un par que tenga el mismo cumpleaños. Si consideramos la función de probabilidad Pr[ n personas tienen al menos un cumpleaños compartido], este promedio determina la media de la distribución, a diferencia de la formulación habitual, que pide la mediana . El problema es relevante para varios algoritmos hash analizados por Donald Knuth en su libro The Art of Computer Programming . Se puede demostrar ^{[20] [21]} que si se toma un muestreo uniforme, con reemplazo, de una población de tamaño M , el número de ensayos necesarios para el primer muestreo repetido de algún individuo tiene el valor esperado n = 1 + Q ( M ). , dónde

${\displaystyle Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.}$

La función

${\displaystyle Q(M)=1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}}+\cdots +{\frac {(M-1)(M-2)\cdots 1}{M^{M-1}}}}$

ha sido estudiado por Srinivasa Ramanujan y tiene expansión asintótica :

${\displaystyle Q(M)\sim {\sqrt {\frac {\pi M}{2}}}-{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi }{2M}}}-{\frac {4}{135M}}+\cdots .}$

Con M = 365 días en un año, el número medio de personas necesarias para encontrar una pareja con el mismo cumpleaños es n = 1 + Q ( M ) ≈ 24,61659 , algo más de 23, el número necesario para un 50% de probabilidad. En el mejor de los casos, bastarán dos personas; en el peor de los casos, se necesita el máximo número posible de M + 1 = 366 personas; pero en promedio sólo se necesitan 25 personas

Un análisis que utilice variables aleatorias indicadoras puede proporcionar un análisis más simple pero aproximado de este problema. ^[22] Para cada par ( i , j ) para k personas en una habitación, definimos la variable aleatoria indicadora X _ij , para , por ${\displaystyle 1\leq i\leq j\leq k}$

$${\displaystyle {\begin{alignedat}{2}X_{ij}&=I\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\[10pt]&={\begin{cases}1,&{\text{if person }}i{\text{ and person }}j{\text{ have the same birthday;}}\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}}$$

$${\displaystyle {\begin{alignedat}{2}E[X_{ij}]&=\Pr\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}={\frac {1}{n}}.\end{alignedat}}}$$

Sea X una variable aleatoria que cuenta los pares de individuos que tienen el mismo cumpleaños.

$${\displaystyle X=\sum _{i=1}^{k}\sum _{j=i+1}^{k}X_{ij}}$$

$${\displaystyle {\begin{alignedat}{3}E[X]&=\sum _{i=1}^{k}\sum _{j=i+1}^{k}E[X_{ij}]\\[8pt]&={\binom {k}{2}}{\frac {1}{n}}\\[8pt]&={\frac {k(k-1)}{2n}}\end{alignedat}}}$$

Para n = 365 , si k = 28 , el número esperado de pares de individuos con el mismo cumpleaños es ⁠28 × 27/2 × 365⁠  ≈ 1,0356. Por lo tanto, podemos esperar al menos una pareja coincidente con al menos 28 personas.

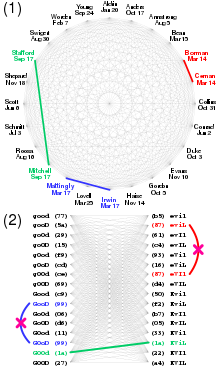
En la Copa Mundial de la FIFA 2014 , cada una de las 32 plantillas contaba con 23 jugadores. Un análisis de las listas oficiales de convocados sugirió que 16 escuadrones tenían parejas de jugadores que compartían cumpleaños, y de estos 5 escuadrones tenían dos parejas: Argentina, Francia, Irán, Corea del Sur y Suiza tenían cada uno dos parejas, y Australia, Bosnia y Herzegovina, Brasil. , Camerún, Colombia, Honduras, Países Bajos, Nigeria, Rusia, España y Estados Unidos cada uno con un par. ^[23]

Voracek, Tran y Formann demostraron que la mayoría de las personas sobreestima marcadamente el número de personas necesarias para lograr una determinada probabilidad de que las personas tengan el mismo cumpleaños, y subestiman notablemente la probabilidad de que las personas tengan el mismo cumpleaños cuando se da un tamaño de muestra específico. . ^[24] Otros resultados mostraron que los estudiantes de psicología y las mujeres obtuvieron mejores resultados en la tarea que los visitantes/personal del casino o los hombres, pero tenían menos confianza en sus estimaciones.

problema inverso

El problema inverso es encontrar, para una probabilidad fija p , el n mayor para el cual la probabilidad p ( n ) es menor que el p dado , o el n más pequeño para el cual la probabilidad p ( n ) es mayor que el p dado . ^{[ cita necesaria ]}

Tomando la fórmula anterior para d  = 365 , se tiene

${\displaystyle n(p;365)\approx {\sqrt {730\ln \left({\frac {1}{1-p}}\right)}}.}$

La siguiente tabla proporciona algunos cálculos de muestra.

Algunos valores que quedan fuera de los límites se han coloreado para mostrar que la aproximación no siempre es exacta.

problema de partición

Un problema relacionado es el problema de la partición , una variante del problema de la mochila de la investigación de operaciones . Algunas pesas se colocan en una balanza ; cada peso es un número entero de gramos elegidos aleatoriamente entre un gramo y un millón de gramos (una tonelada ). La pregunta es si normalmente (es decir, con una probabilidad cercana a 1) se pueden transferir las pesas entre los brazos izquierdo y derecho para equilibrar la balanza. (En caso de que la suma de todos los pesos sea un número impar de gramos, se permite una discrepancia de un gramo.) Si sólo hay dos o tres pesos, la respuesta es muy claramente no; aunque hay algunas combinaciones que funcionan, la mayoría de las combinaciones de tres pesos seleccionadas al azar no lo hacen. Si hay muchísimos pesos, la respuesta es claramente sí. La pregunta es ¿cuántos son suficientes? Es decir, ¿cuál es el número de pesas tales que es tan probable que sea posible equilibrarlas como imposible?

A menudo, la intuición de la gente es que la respuesta está arriba.100 000 . La intuición de la mayoría de las personas es que son miles o decenas de miles, mientras que otros sienten que al menos deberían ser cientos. La respuesta correcta es 23. ^{[ cita necesaria ]}

La razón es que la comparación correcta es el número de particiones de los pesos en izquierda y derecha. Hay 2 ^{N − 1} particiones diferentes para N pesos, y la suma izquierda menos la suma derecha puede considerarse como una nueva cantidad aleatoria para cada partición. La distribución de la suma de pesos es aproximadamente gaussiana , con un pico en500 000 N y ancho1 000 000 √ N , de modo que cuando 2 ^{N − 1} es aproximadamente igual a1 000 000 √ N se produce la transición. 2 ^{23 − 1} es aproximadamente 4 millones, mientras que el ancho de la distribución es sólo 5 millones. ^[25]

En ficción

La novela de Arthur C. Clarke de 1961 , A Fall of Moondust, contiene una sección en la que los personajes principales, atrapados bajo tierra durante un período de tiempo indefinido, celebran un cumpleaños y se encuentran discutiendo la validez del problema del cumpleaños. Como afirmó un físico pasajero: "Si tienes un grupo de más de veinticuatro personas, las probabilidades son mejores que incluso de que dos de ellas tengan el mismo cumpleaños". Finalmente, de los 22 presentes, se revela que dos personajes comparten el mismo cumpleaños, el 23 de mayo.

Notas

1. En su autobiografía, Halmos criticó la forma en que a menudo se presenta la paradoja del cumpleaños, en términos de cálculo numérico. Creía que debería utilizarse como ejemplo en el uso de conceptos matemáticos más abstractos. El escribio:

   El razonamiento se basa en herramientas importantes a las que todos los estudiantes de matemáticas deberían tener fácil acceso. El problema del cumpleaños solía ser un espléndido ejemplo de las ventajas del pensamiento puro sobre la manipulación mecánica; las desigualdades se pueden obtener en uno o dos minutos, mientras que las multiplicaciones tomarían mucho más tiempo y estarían mucho más sujetas a errores, ya sea que el instrumento sea un lápiz o una computadora de escritorio anticuada. Lo que las calculadoras no proporcionan es comprensión, ni facilidad matemática, ni una base sólida para teorías más avanzadas y generalizadas.

Referencias

1. David Singmaster , Fuentes en matemáticas recreativas: una bibliografía comentada , octava edición preliminar, 2004, sección 8.B
2. HSM Coxeter , "Mathematical Recreations and Essays, 11.ª edición", 1940, p. 45, como se informa en IJ Good , Probability and the ponderación de la evidencia , 1950, p. 38
3. Richard Von Mises, "Über Aufteilungs- und Besetzungswahrscheinlichkeiten", Revue de la faculté des sciences de l'Université d'Istanbul 4 :145-163, 1939, reimpreso en Frank, P.; Goldstein, S.; Kac, M.; Prager, W.; Szegö, G.; Birkhoff, G., eds. (1964). Artículos seleccionados de Richard von Mises . vol. 2. Providence, Rhode Island: Amer. Matemáticas. Soc. págs. 313–334.
4. ver Cumpleaños#Distribución a lo largo del año
5. (Floración 1973)
6. Steele, J. Michael (2004). La clase magistral de Cauchy-Schwarz . Cambridge: Prensa de la Universidad de Cambridge. págs.206, 277. ISBN 9780521546775.
7. Mario Cortina Borja; John Haigh (septiembre de 2007). "El problema del cumpleaños". Significado . 4 (3). Real Sociedad de Estadística: 124–127. doi : 10.1111/j.1740-9713.2007.00246.x .
8. Mathis, Frank H. (junio de 1991). "Un problema de cumpleaños generalizado". Revisión SIAM . 33 (2): 265–270. doi :10.1137/1033051. ISSN  0036-1445. JSTOR  2031144. OCLC  37699182.
9. Jim Gray, Catharine van Ingen. Mediciones empíricas de tasas de falla de disco y tasas de error
10. D. Brink, Una solución (probablemente) exacta al problema del cumpleaños, Ramanujan Journal, 2012, [1].
11. Brink 2012, Teorema 2
12. Brink 2012, Teorema 3
13. Brink 2012, Tabla 3, Conjetura 1
14. "Número mínimo de personas para dar un 50% de probabilidad de tener al menos n cumpleaños coincidentes en un año". La enciclopedia en línea de secuencias enteras . OEIS . Consultado el 17 de febrero de 2020 .
15. Suzuki, K.; Tonién, D.; et al. (2006). "Paradoja del cumpleaños de las colisiones múltiples". En Rhee MS, Lee B. (ed.). Apuntes de conferencias sobre informática, vol 4296 . Berlín: Springer. doi :10.1007/11927587_5. Seguridad de la Información y Criptología – ICISC 2006.
16. ZE Schnabel (1938) La estimación de la población total de peces de un lago , American Mathematical Monthly 45 , 348–352.
17. MC Wendl (2003) Probabilidad de colisión entre conjuntos de variables aleatorias , estadísticas y cartas de probabilidad 64 (3), 249–254.
18. M. Abramson y WOJ Moser (1970) Más sorpresas de cumpleaños , American Mathematical Monthly 77 , 856–858
19. Podría, Matt. "Colisiones de hash de colisión con la paradoja del cumpleaños". Blog de Matt Might . Consultado el 17 de julio de 2015 .
20. Knuth, DE (1973). El arte de la programación informática . vol. 3, Clasificación y búsqueda. Reading, Massachusetts: Addison-Wesley. ISBN 978-0-201-03803-3.
21. Flajolet, P.; Grabner, PJ; Kirschenhofer, P.; Prodinger, H. (1995). "Sobre la función Q de Ramanujan". Revista de Matemática Computacional y Aplicada . 58 : 103-116. doi : 10.1016/0377-0427(93)E0258-N .
22. Cormen; et al. Introducción a los algoritmos .
23. Fletcher, James (16 de junio de 2014). "La paradoja del cumpleaños en el Mundial". bbc.com . BBC . Consultado el 27 de agosto de 2015 .
24. Voracek, M.; Tran, Estados Unidos; Formann, Alaska (2008). "Problemas de cumpleaños y pareja de nacimiento: conceptos erróneos sobre la probabilidad entre estudiantes de psicología y visitantes y personal de casinos". Habilidades Perceptuales y Motoras . 106 (1): 91-103. doi :10.2466/pms.106.1.91-103. PMID  18459359. S2CID  22046399.
25. Borgs, C.; Chayés, J.; Pittel, B. (2001). "Transición de fase y escalamiento de tamaño finito en el problema de partición entera". Estructuras aleatorias y algoritmos . 19 (3–4): 247–288. doi :10.1002/rsa.10004. S2CID  6819493.

Bibliografía

• Abramson, M.; Moser, WOJ (1970). "Más sorpresas de cumpleaños". Mensual Matemático Estadounidense . 77 (8): 856–858. doi :10.2307/2317022. JSTOR  2317022.
• Bloom, D. (1973). "Un problema de cumpleaños". Mensual Matemático Estadounidense . 80 (10): 1141-1142. doi :10.2307/2318556. JSTOR  2318556.
• Kemeny, John G.; Snell, J. Laurie; Thompson, Gerald (1957). Introducción a las Matemáticas Finitas (Primera ed.).
• McKinney, EH (1966). "Problema generalizado del cumpleaños". Mensual Matemático Estadounidense . 73 (5): 385–387. doi :10.2307/2315408. JSTOR  2315408.
• Mosteller, F. (1962). "Comprender el problema del cumpleaños". El profesor de matemáticas . 55 (5): 322–325. JSTOR  27956609.Reimpreso en artículos seleccionados de Frederick Mosteller . Serie Springer en Estadística. 2006, págs. 349–353. doi :10.1007/978-0-387-44956-2_21. ISBN 978-0-387-20271-6.
• Schneps, Leila ; Colmez, Coralie (2013). "Error matemático número 5. El caso de Diana Sylvester: análisis del golpe en frío". Matemáticas a prueba. Cómo se utilizan y abusan de los números en los tribunales . Libros básicos. ISBN 978-0-465-03292-1.
• Sy M. Blinder (2013). Guía de matemáticas esenciales: una revisión para estudiantes de física, química e ingeniería. Elsevier. págs. 5–6. ISBN 978-0-12-407163-6.

enlaces externos

• La paradoja del cumpleaños que explica los cumpleaños de los años bisiestos
• Weisstein, Eric W. "Problema de cumpleaños". MundoMatemático .
• Un artículo humorístico que explica la paradoja.
• Experimento de cumpleaños de actividades SOCR EduMaterials
• Comprender el problema del cumpleaños (mejor explicado)
• Eurobirthdays 2012. Un problema de cumpleaños. Un ejemplo práctico futbolístico de la paradoja del cumpleaños.
• Suciedad, James. "23: Probabilidad de cumpleaños". Numéfilo . Brady Harán . Archivado desde el original el 25 de febrero de 2017 . Consultado el 2 de abril de 2013 .
• Calcular las probabilidades del problema del cumpleaños en WolframAlpha