En geometría finita , el plano de Fano (después de Gino Fano ) es un plano proyectivo finito con el menor número posible de puntos y líneas: 7 puntos y 7 líneas, con 3 puntos en cada línea y 3 líneas que pasan por cada punto. Estos puntos y líneas no pueden existir con este patrón de incidencias en la geometría euclidiana , pero se les pueden dar coordenadas usando el campo finito con dos elementos. La notación estándar para este plano, como miembro de una familia de espacios proyectivos , es PG(2, 2) . Aquí, PG significa " geometría proyectiva ", el primer parámetro es la dimensión geométrica (es un plano, de dimensión 2) y el segundo parámetro es el orden (el número de puntos por línea, menos uno).
El plano de Fano es un ejemplo de estructura de incidencia finita , por lo que muchas de sus propiedades pueden establecerse mediante técnicas combinatorias y otras herramientas utilizadas en el estudio de geometrías de incidencia . Al tratarse de un espacio proyectivo, las técnicas algebraicas también pueden ser herramientas eficaces en su estudio.
El plano de Fano se puede construir mediante álgebra lineal como el plano proyectivo sobre el campo finito con dos elementos. De manera similar, se pueden construir planos proyectivos sobre cualquier otro campo finito, siendo el plano de Fano el más pequeño.
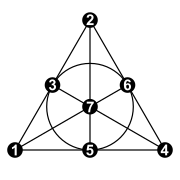
Utilizando la construcción estándar de espacios proyectivos mediante coordenadas homogéneas , los siete puntos del plano de Fano pueden etiquetarse con los siete triples ordenados distintos de cero de dígitos binarios 001, 010, 011, 100, 101, 110 y 111. Esto puede ser hecho de tal manera que por cada dos puntos pyq , el tercer punto en la línea pq tiene la etiqueta formada sumando las etiquetas de pyq módulo 2 dígito por dígito (por ejemplo, 010 y 111, lo que da como resultado 101). En otras palabras, los puntos del plano de Fano corresponden a los puntos distintos de cero del espacio vectorial finito de dimensión 3 sobre el campo finito de orden 2.
Debido a esta construcción, el plano de Fano se considera un plano desarguesiano , aunque el plano es demasiado pequeño para contener una configuración de Desargues no degenerada (que requiere 10 puntos y 10 líneas).
A las líneas del plano de Fano también se les pueden dar coordenadas homogéneas, nuevamente utilizando tripletas de dígitos binarios distintos de cero. Con este sistema de coordenadas, un punto incide sobre una línea si la coordenada del punto y la coordenada de la línea tienen un número par de posiciones en las que ambas tienen bits distintos de cero: por ejemplo, el punto 101 pertenece a la línea 111. , porque tienen bits distintos de cero en dos posiciones comunes. En términos del álgebra lineal subyacente, un punto pertenece a una línea si el producto interno de los vectores que representan el punto y la línea es cero.
Las líneas se pueden clasificar en tres tipos.
Alternativamente, los 7 puntos del plano corresponden a los 7 elementos no identitarios del grupo (Z 2 ) 3 = Z 2 × Z 2 × Z 2 . Las rectas del plano corresponden a los subgrupos de orden 4, isomorfos a Z 2 × Z 2 . El grupo de automorfismo GL(3, 2) del grupo (Z 2 ) 3 es el del plano de Fano y tiene orden 168.
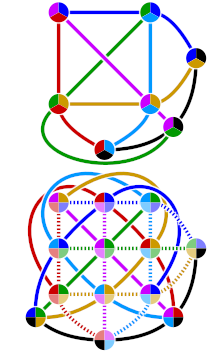
Como ocurre con cualquier estructura de incidencia, el gráfico de Levi del plano de Fano es un gráfico bipartito , representando los vértices de una parte los puntos y la otra las rectas, con dos vértices unidos si el punto y la recta correspondientes son incidentes . Esta gráfica en particular es una gráfica cúbica conexa (regular de grado 3), tiene circunferencia 6 y cada parte contiene 7 vértices. Se trata del gráfico de Heawood , el único de 6 jaulas . [1]
Una colineación , automorfismo o simetría del plano de Fano es una permutación de los 7 puntos que preserva la colinealidad: es decir, lleva puntos colineales (sobre una misma recta) a puntos colineales. Según el teorema fundamental de la geometría proyectiva , el grupo de colineación completo (o grupo de automorfismo , o grupo de simetría ) es el grupo lineal proyectivo PGL(3, 2) , [a] Hirschfeld 1979, p. 131 [2]
Este es un grupo bien conocido de orden 168 = 2 3 ·3·7, el siguiente grupo simple no abeliano después de A 5 de orden 60 (ordenado por tamaño).
Como grupo de permutación que actúa sobre los 7 puntos del plano, el grupo de colineación es doblemente transitivo , lo que significa que cualquier par ordenado de puntos puede asignarse mediante al menos una colineación a cualquier otro par ordenado de puntos. [3] (Ver más abajo).
Las colineaciones también pueden verse como automorfismos que preservan el color del gráfico de Heawood (ver figura).
F 8 es una extensión de campo de grado tres de F 2 , por lo que los puntos del plano de Fano pueden identificarse con F 8 ∖ {0} . El grupo de simetría se puede escribir PGL(3, 2) = Aut( P 2 F 2 ) . De manera similar, PSL(2, 7) = Aut( P 1 F 7 ) . Existe una relación entre los objetos subyacentes, P 2 F 2 y P 1 F 7, llamada mapa de Cat's Cradle. Colorea las siete líneas del plano Fano ROYGBIV, coloca tus dedos en el espacio proyectivo bidimensional en el espacio tridimensional ambiental y estíralos como en el juego infantil Cat's Cradle. Obtendrás un gráfico completo sobre siete vértices con siete triángulos de colores (líneas proyectivas). El origen faltante de F 8 estará en el centro del septágono interior. Ahora etiquete este punto como ∞ y jálelo hacia atrás hasta el origen. Se puede escribir una biyección de F 7 ∪ {∞} a F 8 . Establezca x ∞ = 0 y envíe la pendiente k ↦ x ∞ + x k ∈ F 8 ≅ F 2 [ x ] / ( x 3 + x + 1 ) , donde ahora x k etiqueta los vértices de K 7 con coloración de bordes , observando que f×
8es un grupo cíclico de orden 7. Las simetrías de P 1 F 7 son transformaciones de Möbius , y las transformaciones básicas son reflexiones (orden 2, k ↦ −1/ k ), traslaciones (orden 7, k ↦ k + 1 ) y duplicar (orden 3 ya que 2 3 = 1 , k ↦ 2 k ). Las simetrías correspondientes en el plano de Fano son, respectivamente, intercambiar vértices, rotar el gráfico y rotar triángulos.
Una biyección entre el conjunto de puntos y el conjunto de líneas que preserva la incidencia se llama dualidad y una dualidad de orden dos se llama polaridad . [4]
Las dualidades pueden verse en el contexto del gráfico de Heawood como automorfismos que invierten el color. Un ejemplo de polaridad lo da la reflexión a través de una línea vertical que divide la representación del gráfico de Heawood que se muestra a la derecha. [5] La existencia de esta polaridad muestra que el plano de Fano es autodual . Esto también es una consecuencia inmediata de la simetría entre puntos y rectas en la definición de la relación de incidencia en términos de coordenadas homogéneas, como se detalló en una sección anterior.
El grupo de permutación de los 7 puntos tiene 6 clases de conjugación .
Cada una de estas cuatro estructuras de ciclo define una única clase de conjugación:
La permutación de la identidad
21 permutaciones con dos ciclos de 2
42 permutaciones con 4 ciclos y 2 ciclos.
56 permutaciones con dos 3 ciclos.Las 48 permutaciones con un ciclo completo de 7 forman dos clases de conjugación distintas con 24 elementos:
A se asigna a B , B a C , C a D. Entonces D está en la misma recta que A y B.
A se asigna a B , B a C , C a D. Entonces D está en la misma recta que A y C.(Consulte aquí para obtener una lista completa).
Por lo tanto [ ¿ cómo? ] , según el teorema de enumeración de Pólya , el número de coloraciones no equivalentes del plano de Fano con n colores es (secuencia A241929 en la OEIS ).
En cualquier plano proyectivo, un conjunto de cuatro puntos, de los cuales tres no son colineales, y las seis líneas que unen pares de estos puntos es una configuración conocida como cuadrilátero completo . Las rectas se llaman lados y los pares de lados que no se encuentran en uno de los cuatro puntos se llaman lados opuestos . Los puntos en los que se encuentran lados opuestos se llaman puntos diagonales y hay tres. [6]
Si esta configuración se encuentra en un plano proyectivo y los tres puntos diagonales son colineales, entonces los siete puntos y las siete líneas de la configuración expandida forman un subplano del plano proyectivo que es isomorfo al plano de Fano y se llama subplano de Fano .
Un resultado famoso, debido a Andrew M. Gleason, afirma que si cada cuadrilátero completo en un plano proyectivo finito se extiende hasta un subplano de Fano (es decir, tiene puntos diagonales colineales), entonces el plano es desarguesiano. [7] Gleason llamó a cualquier plano proyectivo que cumpliera esta condición un plano de Fano , creando así cierta confusión con la terminología moderna. Para agravar la confusión, el axioma de Fano establece que los puntos diagonales de un cuadrilátero completo nunca son colineales, una condición que se cumple en los planos proyectivos euclidiano y real. Por tanto, lo que Gleason llamó aviones de Fano no satisfacen el axioma de Fano. [8]
El plano de Fano contiene la siguiente cantidad de configuraciones de puntos y líneas de diferentes tipos. Para cada tipo de configuración, el número de copias de la configuración multiplicado por el número de simetrías del plano que mantienen la configuración sin cambios es igual a 168, el tamaño de todo el grupo de colineación, siempre que cada copia pueda asignarse a cualquier otra copia ( ver teorema del estabilizador de órbita ). Dado que el plano de Fano es autodual, estas configuraciones vienen en pares duales y se puede demostrar que el número de colineaciones que fijan una configuración es igual al número de colineaciones que fijan su configuración dual.
El plano de Fano es un ejemplo de una configuración ( n 3 ) , es decir, un conjunto de n puntos yn líneas con tres puntos en cada línea y tres líneas que pasan por cada punto. El plano de Fano, una configuración (7 3 ), es único y es la configuración más pequeña de este tipo. [10] Según un teorema de Steinitz [11], configuraciones de este tipo se pueden realizar en el plano euclidiano con como máximo una línea curva (todas las demás líneas se encuentran sobre líneas euclidianas). [12]
El plano de Fano es un diseño de bloque simétrico pequeño , específicamente un diseño 2-(7, 3, 1) . Los puntos del diseño son los puntos del plano y los bloques del diseño son las líneas del plano. [13] Como tal, es un ejemplo valioso en la teoría del diseño (de bloques).
Con los puntos etiquetados como 0, 1, 2, ..., 6, las líneas (como conjuntos de puntos) son las traslaciones del conjunto de diferencias planas (7, 3, 1) dado por {0, 1, 3} en el grupo Z. / 7 Z . [13] Con las líneas etiquetadas ℓ 0 , ..., ℓ 6 la matriz de incidencia (tabla) viene dada por:
El avión Fano, como diseño de bloques, es un sistema triple Steiner . [14] Como tal, se le puede dar la estructura de un cuasigrupo . Este cuasigrupo coincide con la estructura multiplicativa definida por los octoniones unitarios e 1 , e 2 , ..., e 7 (omitiendo 1) si se ignoran los signos de los productos de octonión (Báez 2002).
La matroide de Fano F 7 se forma tomando los puntos del plano de Fano como conjunto básico y los subconjuntos no colineales de tres elementos como bases.
El plano de Fano es uno de los ejemplos importantes de la teoría estructural de las matroides . Excluir el plano de Fano como matroide menor es necesario para caracterizar varias clases importantes de matroides, como las regulares , gráficas y cográficas.
Si divide una línea en tres líneas de 2 puntos, obtendrá la "configuración no Fano", que puede incrustarse en el plano real. Es otro ejemplo importante en la teoría matroide, ya que debe excluirse para que se cumplan muchos teoremas.
El plano de Fano se puede extender en una tercera dimensión para formar un espacio proyectivo tridimensional, denotado por PG(3, 2) . Tiene 15 puntos, 35 líneas y 15 planos y es el espacio proyectivo tridimensional más pequeño . [15] También tiene las siguientes propiedades: [16]
