Planos euclidianos en el espacio tridimensional

En la geometría euclidiana , un plano es una superficie plana bidimensional que se extiende indefinidamente . Los planos euclidianos a menudo surgen como subespacios del espacio tridimensional . Un ejemplo prototípico es el de las paredes de una habitación, que se extienden infinitamente y se supone que tienen un espesor infinitesimal. Si bien un par de números reales es suficiente para describir puntos en un plano, la relación con los puntos fuera del plano requiere una consideración especial para su inserción en el espacio circundante . $\mathbb {R} ^{3}$ $\mathbb {R} ^{2}$ $\mathbb {R} ^{3}$

Conceptos derivados

Asegmento plano oUna región plana (o simplemente "plano", en el uso común) es unaregión; es análoga a unsegmento de línea. Un bivector es unsegmento planoorientado los segmentos de línea dirigidos.^[a]Una cara es un segmento plano que delimita unobjeto sólido.^[1]Una losa es una región delimitada por dos planos paralelos. Un paralelepípedo es una región delimitada por tres pares de planos paralelos.

Fondo

Euclides estableció el primer gran hito del pensamiento matemático, un tratamiento axiomático de la geometría. ^[2] Seleccionó un pequeño núcleo de términos no definidos (llamados nociones comunes ) y postulados (o axiomas ) que luego utilizó para demostrar varias afirmaciones geométricas. Aunque el plano en su sentido moderno no recibe una definición directa en ninguna parte de los Elementos , puede considerarse como parte de las nociones comunes. ^{[3] Euclides nunca utilizó números para medir longitud, ángulo o área. El plano euclidiano equipado con un}sistema de coordenadas cartesianas elegido se llama plano cartesiano ; un plano euclidiano no cartesiano equipado con un sistema de coordenadas polares se llamaría plano polar .

Un plano es una superficie reglada .

Plano euclidiano

Sistema de coordenadas cartesianas bidimensional

En matemáticas , un plano euclidiano es un espacio euclidiano de dimensión dos , denotado como . Es un espacio geométrico en el que se requieren dos números reales para determinar la posición de cada punto . Es un espacio afín , que incluye en particular el concepto de líneas paralelas . Tiene también propiedades métricas inducidas por una distancia , lo que permite definir círculos , y la medición de ángulos . ${\textbf {E}}^{2}$ $\mathbb {E} ^{2}$

Un plano euclidiano con un sistema de coordenadas cartesianas elegido se denomina plano cartesiano .

El conjunto de pares ordenados de números reales (el plano de coordenadas reales ), equipado con el producto escalar , a menudo se denomina plano euclidiano o plano euclidiano estándar , ya que todo plano euclidiano es isomorfo a él.

\mathbb {R} ^{2}

Representación

Esta sección se ocupa únicamente de los planos incrustados en tres dimensiones: específicamente, en R 3 .

Determinación por puntos y líneas contenidas

En un espacio euclidiano de cualquier número de dimensiones, un plano está determinado de forma única por cualquiera de los siguientes:

Tres puntos no colineales (puntos que no están en una sola línea).
Una línea y un punto que no está en esa línea.
Dos líneas distintas pero que se cruzan.
Dos líneas distintas pero paralelas .

Propiedades

Las siguientes afirmaciones son válidas en el espacio euclidiano tridimensional, pero no en dimensiones superiores, aunque tienen análogos en dimensiones superiores:

Dos planos distintos son paralelos o se intersecan en una línea .
Una línea es paralela a un plano, lo interseca en un solo punto o está contenida en el plano.
Dos líneas distintas perpendiculares al mismo plano deben ser paralelas entre sí.
Dos planos distintos perpendiculares a la misma línea deben ser paralelos entre sí.

Forma punto-normal y forma general de la ecuación de un plano

De manera análoga a la forma en que las líneas en un espacio bidimensional se describen utilizando una forma punto-pendiente para sus ecuaciones, los planos en un espacio tridimensional tienen una descripción natural utilizando un punto en el plano y un vector ortogonal a él (el vector normal ) para indicar su "inclinación".

En concreto, sea $r 0$ el vector de posición de algún punto $P 0 = (x 0, y 0, z 0)$ , y sea $n = (a, b, c)$ un vector distinto de cero. El plano determinado por el punto $P 0$ y el vector $n$ consta de aquellos puntos $P$ , con vector de posición $r$ , tales que el vector dibujado desde $P 0$ a $P$ es perpendicular a $n$ . Recordando que dos vectores son perpendiculares si y solo si su producto escalar es cero, se deduce que el plano deseado puede describirse como el conjunto de todos los puntos $r$ tales que El punto aquí significa un producto escalar . Desarrollado esto se convierte en que es la forma punto-normal de la ecuación de un plano. ^[4] Esta es solo una ecuación lineal donde que es la forma desarrollada de ${\boldsymbol {n}}\cdot ({\boldsymbol {r}}-{\boldsymbol {r}}_{0})=0.$
$a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0,$ $ax+by+cz+d=0,$ $d=-(ax_{0}+by_{0}+cz_{0}),$ $-{\boldsymbol {n}}\cdot {\boldsymbol {r}}_{0}.$

En matemáticas es una convención común expresar la normal como un vector unitario , pero el argumento anterior es válido para un vector normal de cualquier longitud distinta de cero.

Por el contrario, se demuestra fácilmente que si $a$ , $b$ , $c$ y $d$ son constantes y $a$ , $b$ y $c$ no son todos cero, entonces la gráfica de la ecuación es un plano que tiene como normal el vector $n$ $= ($ $a$ $,$ $b$ $,$ $c$ $) .$ ^[5] Esta ecuación familiar para un plano se denomina forma general de la ecuación del plano o simplemente ecuación del plano . ^[6] $ax+by+cz+d=0,$

Así, por ejemplo, una ecuación de regresión de la forma $y = d + ax + cz$ (con $b = -1$ ) establece un plano de mejor ajuste en el espacio tridimensional cuando hay dos variables explicativas.

Describir un plano con un punto y dos vectores que se encuentran sobre él

Alternativamente, un plano puede describirse paramétricamente como el conjunto de todos los puntos de la forma ${\boldsymbol {r}}={\boldsymbol {r}}_{0}+s{\boldsymbol {v}}+t{\boldsymbol {w}},$

donde $s$ y $t$ abarcan todos los números reales, $v$ y $w$ son vectores linealmente independientes que definen el plano y $r$ $0$ es el vector que representa la posición de un punto arbitrario (pero fijo) en el plano. Los vectores $v$ y $w$ pueden visualizarse como vectores que comienzan en $r$ $0$ y apuntan en diferentes direcciones a lo largo del plano. Los vectores $v$ y $w$ pueden ser perpendiculares , pero no paralelos.

Describiendo un plano a través de tres puntos

Sean $p 1 = (x 1, y 1, z 1)$ , $p 2 = (x 2, y 2, z 2)$ y $p 3 = (x 3, y 3, z 3)$ puntos no colineales.

Método 1

El plano que pasa por $p 1$ , $p 2$ y $p 3$ puede describirse como el conjunto de todos los puntos ( x , y , z ) que satisfacen las siguientes ecuaciones determinantes : ${\begin{vmatrix}x-x_{1}&y-y_{1}&z-z_{1}\\x_{2}-x_{1}&y_{2}-y_{1}&z_{2 }-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\end{vmatrix}}={\begin{vmatrix}x- x_ {1} & y-y_ {1} & z-z_ {1} \\ x-x_ {2} & y-y_ {2} & z-z_ {2} \\ x-x_ {3} & y-y_ {3} &z-z_{3}\end{vmatrix}}=0.$

Método 2

Para describir el plano mediante una ecuación de la forma , resuelva el siguiente sistema de ecuaciones: $ax+by+cz+d=0$ $ax_{1}+by_{1}+cz_{1}+d=0$ $ax_{2}+by_{2}+cz_{2}+d=0$ $ax_{3}+by_{3}+cz_{3}+d=0.$

Este sistema se puede resolver utilizando la regla de Cramer y manipulaciones matriciales básicas. Sea $D={\begin{vmatrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3 }\end{vmatrix}}.$

Si $D$ no es cero (es decir, para planos que no pasan por el origen), los valores de $a$ , $b$ y $c$ se pueden calcular de la siguiente manera: $a={\frac {-d}{D}}{\begin{vmatrix}1&y_{1}&z_{1}\\1&y_{2}&z_{2}\\1&y_{3}&z_{3} \end{vmatriz}}$ $b={\frac {-d}{D}}{\begin{vmatrix}x_{1}&1&z_{1}\\x_{2}&1&z_{2}\\x_{3}&1&z_{3} \end{vmatriz}}$ $c={\frac {-d}{D}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{ 3}&1\end{vmatrix}}.$

Estas ecuaciones son paramétricas en d . Si se establece d igual a cualquier número distinto de cero y se lo sustituye en estas ecuaciones, se obtendrá un conjunto de soluciones.

Método 3

Este plano también se puede describir mediante la § Forma normal puntual y forma general de la ecuación de un plano que se describe anteriormente. Un vector normal adecuado se obtiene mediante el producto vectorial y el punto $r$ $0$ se puede tomar como cualquiera de los puntos $p$ $1$ , $p$ $2$ o $p$ $3$ ^[7] (o cualquier otro punto en el plano). ${\boldsymbol {n}}=({\boldsymbol {p}}_{2}-{\boldsymbol {p}}_{1})\times ({\boldsymbol {p}}_{3}-{\boldsymbol {p}}_{1}),$

Operaciones

Distancia de un punto a un plano

En el espacio euclidiano , la distancia de un punto a un plano es la distancia entre un punto dado y su proyección ortogonal en el plano, la distancia perpendicular al punto más cercano en el plano.

Se puede encontrar a partir de un cambio de variables que desplaza el origen para que coincida con el punto dado y luego se busca el punto en el plano desplazado que esté más cerca del origen . El punto resultante tiene coordenadas cartesianas : $ax+by+cz=d$ ${\estilo de visualización (x,y,z)}$

\displaystyle x={\frac {ad}{a^{2}+b^{2}+c^{2}}},\quad \quad \displaystyle y={\frac {bd}{a^{2}+b^{2}+c^{2}}},\quad \quad \displaystyle z={\frac {cd}{a^{2}+b^{2}+c^{2}}}

La distancia entre el origen y el punto es .

(x,y,z)

{\sqrt {x^{2}+y^{2}+z^{2}}}

Intersección de línea y plano

En geometría analítica , la intersección de una línea y un plano en el espacio tridimensional puede ser el conjunto vacío , un punto o una línea. Es la línea completa si esa línea está inserta en el plano, y es el conjunto vacío si la línea es paralela al plano pero está fuera de él. De lo contrario, la línea corta el plano en un solo punto.

La distinción entre estos casos y la determinación de ecuaciones para el punto y la línea en los últimos casos tienen utilidad en gráficos de computadora , planificación de movimiento y detección de colisiones .

Línea de intersección entre dos planos

En geometría analítica , la intersección de dos planos en el espacio tridimensional es una línea .

Intersección esfera-plano

Cuando la intersección de una esfera y un plano no es un punto vacío o único, se trata de un círculo. Esto se puede ver de la siguiente manera:

Sea S una esfera con centro O , P un plano que interseca a S . Dibuje OE perpendicular a P y que corte a P en E . Sean A y B dos puntos diferentes en la intersección. Entonces AOE y BOE son triángulos rectángulos con un lado común, OE , y las hipotenusas AO y BO iguales. Por lo tanto, los lados restantes AE y BE son iguales. Esto demuestra que todos los puntos en la intersección están a la misma distancia del punto E en el plano P , en otras palabras, todos los puntos en la intersección se encuentran en un círculo C con centro E . ^[8] Esto demuestra que la intersección de P y S está contenida en C . Nótese que OE es el eje del círculo.

Consideremos ahora un punto D del círculo C . Como C se encuentra en P , también lo está D . Por otra parte, los triángulos AOE y DOE son triángulos rectángulos con un lado común, OE , y los catetos EA y ED son iguales. Por lo tanto, las hipotenusas AO y DO son iguales, e iguales al radio de S , de modo que D se encuentra en S . Esto demuestra que C está contenido en la intersección de P y S .

Como corolario, en una esfera hay exactamente un círculo que puede trazarse a través de tres puntos dados. ^[9]

La prueba puede ampliarse para mostrar que los puntos de un círculo están todos a una distancia angular común desde uno de sus polos. ^[10]

Compárense también las secciones cónicas , que pueden producir óvalos .

Ocurrencia en la naturaleza

Un plano sirve como modelo matemático para muchos fenómenos físicos, como la reflexión especular en un espejo plano o los frentes de onda en una onda plana viajera . La superficie libre de líquidos no perturbados tiende a ser casi plana (ver planitud ). La superficie más plana jamás fabricada es un espejo atómico estabilizado cuánticamente. ^[11] En astronomía, se utilizan varios planos de referencia para definir posiciones en órbita. Los planos anatómicos pueden ser laterales ("sagital"), frontales ("coronales") o transversales. En geología, los lechos (capas de sedimentos) a menudo son planos. Los planos están involucrados en diferentes formas de imágenes , como el plano focal , el plano de imagen y el plano de imagen .

Índices de Miller

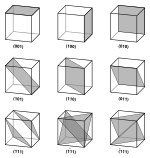
La actitud de un plano reticular es la orientación de la línea normal al plano, ^[12] y se describe mediante los índices de Miller del plano . En el espacio tridimensional, una familia de planos (una serie de planos paralelos) se puede denotar mediante sus índices de Miller ( hkl ), ^[13]^[14] por lo que la familia de planos tiene una actitud común a todos sus planos constituyentes.

Huelga y inmersión

Línea de rumbo y pendiente de un avión que describe la actitud relativa a un plano horizontal y un plano vertical perpendicular a la línea de rumbo

Muchas de las características que se observan en geología son planos o líneas, y su orientación se conoce comúnmente como actitud . Estas actitudes se especifican con dos ángulos.

En el caso de una línea, estos ángulos se denominan tendencia y caída . La tendencia es la dirección de la brújula de la línea y la caída es el ángulo descendente que forma con un plano horizontal. ^[15]

En el caso de un plano, los dos ángulos se denominan rumbo (ángulo) y buzamiento (ángulo) . Una línea de rumbo es la intersección de un plano horizontal con la característica plana observada (y, por lo tanto, una línea horizontal), y el ángulo de rumbo es el rumbo de esta línea (es decir, en relación con el norte geográfico o con respecto al norte magnético ). El buzamiento es el ángulo entre un plano horizontal y la característica plana observada, tal como se observa en un tercer plano vertical perpendicular a la línea de rumbo.

Véase también

Notas

Notas explicativas

^ Más precisamente, una entidad algebraica análoga a una clase de equivalencia de segmentos planos orientados.

Citas

^ Diccionario colegiado de Merriam-Webster (undécima edición). Springfield, MA: Merriam-Webster . 2004.
^ Eves 1963, pág. 19
^ Joyce, DE (1996), Elementos de Euclides, Libro I, Definición 7, Clark University , consultado el 8 de agosto de 2009
^ Anton 1994, pág. 155
^ Anton 1994, pág. 156
^ Weisstein, Eric W. (2009), "Plane", MathWorld--A Wolfram Web Resource , consultado el 8 de agosto de 2009
^ Dawkins, Paul, "Ecuaciones de planos", Cálculo III
^ La prueba sigue a Hobbs, Prop. 304
^ Hobbs, Proposición 308
^ Hobbs, Proposición 310
^ Evans, Jon (22 de agosto de 2008). «La superficie más lisa jamás vista es un espejo para los átomos». New Scientist . Consultado el 5 de marzo de 2023 .
^ William Anthony Granville (1904). "§178 Línea normal a una superficie". Elementos del cálculo diferencial e integral. Ginn & Company. pág. 275.
^ Augustus Edward Hough Love (1892). Tratado sobre la teoría matemática de la elasticidad. Vol. 1. Cambridge University Press. pág. 79 y siguientes .
^ Marcus Frederick Charles Ladd; Rex Alfred Palmer (2003). "§2.3 Familias de planos y espaciamientos interplanares". Determinación de la estructura mediante cristalografía de rayos X (4.ª ed.). Springer. pág. 62 y siguientes . ISBN 0-306-47454-9.
^ Stephen Mark Rowland; Ernest M. Duebendorfer; Ilsa M. Schiefelbein (2007). "Actitudes de líneas y planos". Análisis estructural y síntesis: un curso de laboratorio en geología estructural (3.ª ed.). Wiley-Blackwell. pág. 1 y siguientes . ISBN 978-1-4051-1652-7.

Referencias

Anton, Howard (1994), Álgebra lineal elemental (7.ª ed.), John Wiley & Sons, ISBN 0-471-58742-7
Eves, Howard (1963), Un estudio de geometría , vol. I, Boston: Allyn y Bacon, Inc.
Hobbs, Charles Austen (1921). Geometría sólida. Cambridge, GH Kent. págs. 396-400. LCCN 21016427.

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Planos euclidianos en el espacio tridimensional .

"Plano", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
Weisstein, Eric W. "Avión". MathWorld .
"Aliviando la dificultad de la aritmética y la geometría plana" es un manuscrito árabe, del siglo XV, que sirve como tutorial sobre geometría plana y aritmética.