Mecánica de contacto por fricción.

Estudio de la deformación de cuerpos en presencia de efectos de fricción.

La mecánica de contacto es el estudio de la deformación de sólidos que se tocan entre sí en uno o más puntos. ^{[1] [2]} Esto se puede dividir en fuerzas de compresión y adherencia en la dirección perpendicular a la interfaz, y fuerzas de fricción en la dirección tangencial. La mecánica de contacto por fricción es el estudio de la deformación de los cuerpos en presencia de efectos de fricción, mientras que la mecánica de contacto sin fricción supone la ausencia de tales efectos.

La mecánica de contacto por fricción se ocupa de una amplia gama de escalas diferentes.

• A escala macroscópica, se aplica para la investigación del movimiento de cuerpos en contacto (ver Dinámica de contacto ). Por ejemplo, el rebote de una pelota de goma sobre una superficie depende de la interacción de fricción en la interfaz de contacto. Aquí la principal preocupación es la fuerza total versus la indentación y el desplazamiento lateral.
• En la escala intermedia, uno está interesado en las tensiones , deformaciones y deformaciones locales de los cuerpos en contacto dentro y cerca del área de contacto. Por ejemplo, para derivar o validar modelos de contacto a escala macroscópica, o para investigar el desgaste y daño de las superficies de los cuerpos en contacto. Las áreas de aplicación de esta escala son la interacción neumático-pavimento, la interacción rueda-carril del ferrocarril, el análisis de rodamientos, etc.
• Finalmente, a escala microscópica y nanométrica, la mecánica de contacto se utiliza para aumentar nuestra comprensión de los sistemas tribológicos (por ejemplo, investigar el origen de la fricción ) y para la ingeniería de dispositivos avanzados como microscopios de fuerza atómica y dispositivos MEMS .

Esta página se ocupa principalmente de la segunda escala: obtener información básica sobre las tensiones y deformaciones en y cerca de la zona de contacto, sin prestar demasiada atención a los mecanismos detallados por los cuales se producen.

Historia

Varios científicos, ingenieros y matemáticos famosos contribuyeron a nuestra comprensión de la fricción. ^[3] Incluyen a Leonardo da Vinci , Guillaume Amontons , John Theophilus Desaguliers , Leonhard Euler y Charles-Augustin de Coulomb . Más tarde, Nikolai Pavlovich Petrov , Osborne Reynolds y Richard Stribeck complementaron esta comprensión con teorías de la lubricación .

La deformación de materiales sólidos fue investigada en los siglos XVII y XVIII por Robert Hooke , Joseph Louis Lagrange , y en los siglos XIX y XX por d'Alembert y Timoshenko . Respecto a la mecánica de contactos destaca la aportación clásica de Heinrich Hertz ^{[4] .} Además, las soluciones fundamentales de Boussinesq y Cerruti son de primordial importancia para la investigación de problemas de contacto por fricción en el régimen (linealmente) elástico .

En aplicaciones ferroviarias, se desea conocer la relación entre la fuga (diferencia de velocidad) y la fuerza de fricción . ${\displaystyle \xi }$ ${\displaystyle F_{w}}$

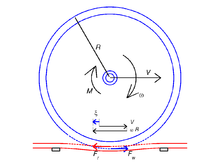
Los resultados clásicos para un verdadero problema de contacto por fricción se refieren a los artículos de FW Carter (1926) y H. Fromm (1927). Presentaron de forma independiente la relación de fluencia versus fuerza de fluencia para un cilindro en un plano o para dos cilindros en contacto rodante estable utilizando la ley de fricción seca de Coulomb (ver más abajo). ^[5] Estos se aplican a la tracción de locomotoras ferroviarias y para comprender la oscilación de caza de los vehículos ferroviarios. Con respecto al deslizamiento, las soluciones clásicas se deben a C. Cattaneo (1938) y RD Mindlin (1949), quienes consideraron el desplazamiento tangencial de una esfera sobre un plano (ver más abajo). ^[1]

En la década de 1950 creció el interés por el contacto de rodadura de las ruedas de ferrocarril. En 1958, Kenneth L. Johnson presentó un enfoque aproximado para el problema de fricción 3D con geometría hertziana, con fuga lateral o de espín. Entre otras cosas, descubrió que la fuga del espín, que es simétrica con respecto al centro de la zona de contacto, conduce a una fuerza lateral neta en condiciones de rodadura. Esto se debe a las diferencias longitudinales en la distribución de las tracciones en la zona de contacto.

En 1967, Joost Jacques Kalker publicó su importante tesis doctoral sobre la teoría lineal del contacto rodante. ^[6] Esta teoría es exacta para la situación de un coeficiente de fricción infinito, en cuyo caso el área de deslizamiento desaparece, y es aproximada para fugas que no desaparecen. Supone la ley de fricción de Coulomb, que requiere más o menos superficies (escrupulosamente) limpias. Esta teoría es para cuerpos masivos como el contacto rueda-carril del ferrocarril. Con respecto a la interacción carretera-neumático, una contribución importante se refiere a la llamada fórmula mágica del neumático de Hans Pacejka . ^[7]

En la década de 1970 se idearon muchos modelos numéricos. Enfoques particularmente variacionales , como los que se basan en las teorías de existencia y unicidad de Duvaut y Lion. Con el tiempo, estos se convirtieron en enfoques de elementos finitos para problemas de contacto con geometrías y modelos de materiales generales, y en enfoques basados ​​en el medio espacio para los llamados problemas de contacto de bordes lisos para materiales linealmente elásticos. Los modelos de la primera categoría fueron presentados por Laursen ^[8] y Wriggers. ^[9] Un ejemplo de la última categoría es el modelo CONTACT de Kalker. ^[10]

Un inconveniente de los métodos variacionales bien fundamentados es su elevado tiempo de cálculo. Por lo tanto, también se idearon muchos enfoques aproximados diferentes. Varias teorías aproximadas bien conocidas para el problema del contacto rodante son el enfoque FASTSIM de Kalker, la fórmula Shen-Hedrick-Elkins y el enfoque de Polach.

En el artículo de Knothe se proporciona más información sobre la historia del problema de contacto rueda/carril. ^[5] Además, Johnson recopiló en su libro una enorme cantidad de información sobre la mecánica de contacto y temas relacionados. ^[1] Con respecto a la mecánica de contacto rodante, Kalker también presenta una visión general de varias teorías. ^[10] Finalmente, son de interés las actas de un curso CISM, que proporcionan una introducción a aspectos más avanzados de la teoría del contacto rodante. ^[11]

Formulación del problema

En el análisis de los problemas de contacto por fricción es fundamental comprender que las tensiones en la superficie de cada cuerpo varían espacialmente. En consecuencia, las tensiones y deformaciones de los cuerpos también varían con la posición. Y el movimiento de las partículas de los cuerpos en contacto puede ser diferente en diferentes lugares: en una parte de la zona de contacto, las partículas de los cuerpos opuestos pueden adherirse (pegarse) entre sí, mientras que en otras partes de la zona de contacto se produce un movimiento relativo. Este deslizamiento relativo local se llama microdeslizamiento .

Esta subdivisión del área de contacto en áreas de adherencia y deslizamiento se manifiesta, entre otras cosas, en el desgaste por fricción . Tenga en cuenta que el desgaste ocurre sólo donde se disipa la potencia , lo que requiere tensión y desplazamiento relativo local (deslizamiento) entre las dos superficies.

El tamaño y la forma de la propia zona de contacto y de sus zonas de adherencia y deslizamiento generalmente se desconocen de antemano. Si se conocieran, entonces los campos elásticos en los dos cuerpos podrían resolverse independientemente uno del otro y el problema ya no sería un problema de contacto.

En un problema de contacto se pueden distinguir tres componentes diferentes.

1. En primer lugar, se produce la deformación de los cuerpos separados como reacción a las cargas aplicadas sobre sus superficies. Este es el tema de la mecánica general del continuo . Depende en gran medida de la geometría de los cuerpos y de su comportamiento material ( constitutivo ) (por ejemplo, respuesta elástica versus plástica , estructura homogénea versus estratificada, etc.).
2. En segundo lugar, está el movimiento general de los cuerpos entre sí. Por ejemplo, los cuerpos pueden estar en reposo (estática) o acercándose rápidamente uno al otro ( impacto ), y pueden desplazarse (deslizarse) o rotarse ( rodar ) uno sobre el otro. Estos movimientos generales se estudian generalmente en la mecánica clásica , véase, por ejemplo, la dinámica multicuerpo .
3. Finalmente están los procesos en la interfaz de contacto : compresión y adhesión en la dirección perpendicular a la interfaz, y fricción y microdeslizamiento en las direcciones tangenciales .

El último aspecto es la principal preocupación de la mecánica de contactos. Se describe en términos de las llamadas condiciones de contacto . Para la dirección perpendicular a la interfaz, el problema de contacto normal, los efectos de adhesión suelen ser pequeños (a escalas espaciales más grandes) y normalmente se emplean las siguientes condiciones:

1. El espacio entre las dos superficies debe ser nulo (contacto) o estrictamente positivo (separación ); ${\displaystyle e_{n}}$ ${\displaystyle e_{n}>0}$
2. La tensión normal que actúa sobre cada cuerpo es nula (separación) o de compresión ( en contacto). ${\displaystyle p_{n}}$ ${\displaystyle p_{n}>0}$

Matemáticamente: . Aquí hay funciones que varían con la posición a lo largo de las superficies de los cuerpos. ${\displaystyle e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\!}$ ${\displaystyle e_{n},p_{n}}$

En las direcciones tangenciales se suelen utilizar las siguientes condiciones:

1. El esfuerzo cortante local (tangencial) (asumiendo la dirección normal paralela al eje) no puede exceder un cierto máximo dependiente de la posición, el llamado límite de tracción ; ${\displaystyle {\vec {p}}=(p_{x},p_{y})^{\mathsf {T}}\,\!}$ ${\displaystyle z}$ ${\displaystyle g}$
2. Cuando la magnitud de la tracción tangencial cae por debajo del límite de tracción , las superficies opuestas se adhieren entre sí y el microdeslizamiento desaparece ; ${\displaystyle \|{\vec {p}}\|<g\,\!}$ ${\displaystyle {\vec {s}}=(s_{x},s_{y})^{\mathsf {T}}={\vec {0}}\,\!}$
3. El microdeslizamiento ocurre cuando las tracciones tangenciales están en el límite de tracción; la dirección de la tracción tangencial es entonces opuesta a la dirección del microdeslizamiento . ${\displaystyle {\vec {p}}=-g{\vec {s}}/\|{\vec {s}}\|\,\!}$

La forma exacta de la cota de tracción es la llamada ley de fricción local. Para esto, la ley de fricción (global) de Coulomb a menudo se aplica localmente: , con el coeficiente de fricción. También son posibles fórmulas más detalladas, por ejemplo dependiendo de la temperatura , la velocidad de deslizamiento local , etc. ${\displaystyle \|{\vec {p}}\|\leq g=\mu p_{n}\,\!}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle T}$ ${\displaystyle \|{\vec {s}}\|}$

Soluciones para casos estáticos

Cuerda sobre un bolardo, la ecuación del cabrestante

Ilustración de una cuerda elástica enrollada alrededor de un elemento fijo, como un bolardo. El área de contacto se divide en zonas de adherencia y de deslizamiento, dependiendo de las cargas ejercidas en ambos extremos y del historial de carga.

Considere una cuerda donde se ejercen fuerzas iguales (p. ej., ) en ambos lados. De este modo, la cuerda se estira un poco y se induce una tensión interna ( en cada posición a lo largo de la cuerda). La cuerda se enrolla alrededor de un elemento fijo, como un bolardo ; está doblado y hace contacto con la superficie del artículo en un ángulo de contacto (por ejemplo, ). Entre el cable y el bolardo se genera una presión normal, pero todavía no se produce fricción. A continuación, la fuerza en un lado del bolardo se aumenta a un valor mayor (p. ej., ). Esto causa tensiones de corte por fricción en el área de contacto. En la situación final el bolardo ejerce una fuerza de fricción sobre la cuerda tal que se produce una situación estática. ${\displaystyle F_{\text{hold}}=400\,\mathrm {N} }$ ${\displaystyle T}$ ${\displaystyle T=400\,\mathrm {N} }$ ${\displaystyle 180^{\circ }}$ ${\displaystyle F_{\text{load}}=600\,\mathrm {N} }$

La distribución de tensiones en el cable en esta situación final se describe mediante la ecuación del cabrestante , con solución:

${\displaystyle {\begin{aligned}T(\phi )&=T_{\text{hold}},&\phi &\in \left[\phi _{\text{hold}},\phi _{\text{intf}}\right]\\T(\phi )&=T_{\text{load}}e^{-\mu \phi },&\phi &\in \left[\phi _{\text{intf}},\phi _{\text{load}}\right]\\\phi _{\text{intf}}&={\frac {1}{\mu }}\log \left({\frac {T_{\text{load}}}{T_{\text{hold}}}}\right)&\end{aligned}}}$

La tensión aumenta desde el lado flojo ( ) hasta el lado alto . Cuando se ve desde el lado alto, la tensión cae exponencialmente, hasta que alcanza la carga inferior en . A partir de ahí es constante en este valor. El punto de transición está determinado por la relación de las dos cargas y el coeficiente de fricción. Aquí las tensiones están en Newtons y los ángulos en radianes. ${\displaystyle T_{\text{hold}}}$ ${\displaystyle \phi =\phi _{\text{hold}}}$ ${\displaystyle T_{\text{load}}}$ ${\displaystyle \phi =\phi _{\text{load}}}$ ${\displaystyle \phi =\phi _{\text{intf}}}$ ${\displaystyle \phi _{\text{intf}}}$ ${\displaystyle T}$ ${\displaystyle \phi }$

La tensión en la cuerda en la situación final aumenta respecto al estado inicial. Por tanto, la cuerda se alarga un poco. Esto significa que no todas las partículas superficiales del cable pueden haber mantenido su posición inicial en la superficie del bolardo. Durante el proceso de carga, la cuerda se deslizó un poco a lo largo de la superficie del bolardo en el área de deslizamiento . Este deslizamiento es precisamente lo suficientemente grande como para llegar al alargamiento que se produce en el estado final. Tenga en cuenta que no se produce ningún deslizamiento en el estado final; El término área de deslizamiento se refiere al deslizamiento que ocurrió durante el proceso de carga. Tenga en cuenta además que la ubicación del área de deslizamiento depende del estado inicial y del proceso de carga. Si la tensión inicial es y la tensión se reduce al lado flojo, entonces el área de deslizamiento ocurre en el lado flojo del área de contacto. Para tensiones iniciales entre y , puede haber áreas de deslizamiento en ambos lados con un área de palo en el medio. ${\displaystyle T}$ ${\displaystyle \phi \in [\phi _{\text{intf}},\phi _{\text{load}}]}$ ${\displaystyle 600\,\mathrm {N} }$ ${\displaystyle 400\,\mathrm {N} }$ ${\displaystyle 400}$ ${\displaystyle 600\,\mathrm {N} }$

Generalización para una cuerda que descansa sobre una superficie ortotrópica arbitraria.

Si una cuerda se encuentra en equilibrio bajo fuerzas tangenciales sobre una superficie ortotrópica rugosa, entonces se satisfacen las tres condiciones siguientes (todas ellas):

1. Sin separación: la reacción normal es positiva para todos los puntos de la curva de la cuerda: ${\displaystyle N}$

   ${\displaystyle N=-k_{n}T>0}$, donde es una curvatura normal de la curva de la cuerda. ${\displaystyle k_{n}}$

2. El coeficiente de fricción y el ángulo de arrastre satisfacen los siguientes criterios para todos los puntos de la curva. ${\displaystyle \mu _{g}}$ ${\displaystyle \alpha }$
   ${\displaystyle -\mu _{g}<\tan \alpha <+\mu _{g}}$
3. Valores límite de las fuerzas tangenciales:

   Las fuerzas en ambos extremos de la cuerda satisfacen la siguiente desigualdad ${\displaystyle T}$ ${\displaystyle T_{0}}$

   ${\displaystyle T_{0}e^{-\int _{s}\omega \mathrm {d} s}\leq T\leq T_{0}e^{\int _{s}\omega \mathrm {d} s}}$

   con , ${\displaystyle \omega =\mu _{\tau }{\sqrt {k_{n}^{2}-{\frac {k_{g}^{2}}{\mu _{g}^{2}}}}}=\mu _{\tau }k{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}$

   donde es una curvatura geodésica de la curva de la cuerda, es una curvatura de una curva de la cuerda, es un coeficiente de fricción en la dirección tangencial. ${\displaystyle k_{g}}$ ${\displaystyle k}$ ${\displaystyle \mu _{\tau }}$

   Si es constante entonces . ${\displaystyle \omega }$ ${\displaystyle T_{0}e^{-\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}\leq T\leq T_{0}e^{\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}}$

Esta generalización ha sido obtenida por Konyukhov A., ^{[12] [13]}

Esfera en un avión, el problema (3D) de Cattaneo

Considere una esfera que se presiona contra un plano (medio espacio) y luego se desplaza sobre la superficie del plano. Si la esfera y el plano se idealizan como cuerpos rígidos, entonces el contacto se produciría en un solo punto y la esfera no se movería hasta que la fuerza tangencial que se aplica alcance la fuerza de fricción máxima. Luego comienza a deslizarse sobre la superficie hasta que la fuerza aplicada se reduce nuevamente.

En realidad, si se tienen en cuenta los efectos elásticos, la situación es muy diferente. Si se presiona una esfera elástica sobre un plano elástico del mismo material, ambos cuerpos se deforman, se crea una superficie de contacto circular y se produce una distribución de presión normal (hertziana). El centro de la esfera se mueve hacia abajo una distancia llamada aproximación , que equivale a la máxima penetración de las superficies no deformadas. Para una esfera de radio y constantes elásticas, esta solución hertziana dice: ${\displaystyle \delta _{n}}$ ${\displaystyle R}$ ${\displaystyle E,\nu }$

${\displaystyle {\begin{aligned}p_{n}(x,y)&=p_{0}{\sqrt {1-{\frac {r^{2}}{a^{2}}}}}&r&={\sqrt {x^{2}+y^{2}}}\leq a&a&={\sqrt {R\delta _{n}}}\\p_{0}&={\frac {2}{\pi }}E^{*}{\sqrt {\frac {\delta _{n}}{R}}}&F_{n}&={\frac {4}{3}}E^{*}{\sqrt {R}}\delta _{n}^{\frac {3}{2}}&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}\end{aligned}}}$

Ahora considere que se aplica una fuerza tangencial que es menor que el límite de fricción de Coulomb . Luego, el centro de la esfera se moverá hacia los lados una pequeña distancia que se llama desplazamiento . Se obtiene un equilibrio estático en el que se producen deformaciones elásticas así como tensiones de corte por fricción en la interfaz de contacto. En este caso, si se reduce la fuerza tangencial, las deformaciones elásticas y los esfuerzos cortantes también se reducen. La esfera regresa en gran medida a su posición original, excepto por las pérdidas por fricción que surgen debido al deslizamiento local en la zona de contacto. ${\displaystyle F_{x}}$ ${\displaystyle \mu F_{n}}$ ${\displaystyle \delta _{x}}$

Cattaneo resolvió aproximadamente este problema de contacto mediante un enfoque analítico. La distribución de tensiones en el estado de equilibrio consta de dos partes:

${\displaystyle {\begin{aligned}p_{x}(x,y)&=\mu p_{0}\left({\sqrt {1-{\frac {r^{2}}{a^{2}}}}}-{\frac {c}{a}}{\sqrt {1-{\frac {r^{2}}{c^{2}}}}}\right)&0\leq {}&r\leq c\\p_{x}(x,y)&=\mu p_{n}(x,y)&c\leq {}&r\leq a\\p_{x}(x,y)&=0&a\leq {}&r\end{aligned}}}$

En la región central pegajosa , las partículas superficiales del plano se desplazan hacia la derecha, mientras que las partículas superficiales de la esfera se desplazan hacia la izquierda. Aunque la esfera en su conjunto se mueve con respecto al plano, estas partículas superficiales no se mueven entre sí. En el anillo exterior , las partículas de la superficie se movían entre sí. Su desplazamiento local se obtiene como ${\displaystyle 0\leq r\leq c}$ ${\displaystyle u_{x}=\delta _{x}/2}$ ${\displaystyle u_{x}=-\delta _{x}/2}$ ${\displaystyle \delta _{x}}$ ${\displaystyle c\leq r\leq a}$

${\displaystyle s_{x}(x,y)=\delta _{x}+u_{x}^{\text{sphere}}(x,y)-u_{x}^{\text{plane}}(x,y)}$

Este desplazamiento es precisamente tan grande que se obtiene un equilibrio estático con tensiones de corte en la tracción limitada en esta llamada zona de deslizamiento. ${\displaystyle s_{x}(x,y)}$

Entonces, durante la carga tangencial de la esfera, se produce un deslizamiento parcial . De este modo, el área de contacto se divide en un área de deslizamiento donde las superficies se mueven entre sí y un área de adherencia donde no lo hacen. En el estado de equilibrio no se produce más deslizamiento.

Soluciones para problemas de deslizamiento dinámico.

La solución de un problema de contacto consiste en el estado en la interfaz (dónde está el contacto, división del área de contacto en zonas de adherencia y deslizamiento, y las distribuciones de tensión normal y cortante) más el campo elástico en el interior de los cuerpos. Esta solución depende del historial del contacto. Esto puede verse como una extensión del problema de Cattaneo descrito anteriormente.

• En el problema de Cattaneo, primero se presiona la esfera sobre el plano y luego se desplaza tangencialmente. Esto produce un deslizamiento parcial como se describe anteriormente.
• Si primero se desplaza la esfera tangencialmente y luego se presiona sobre el plano, entonces no hay diferencia de desplazamiento tangencial entre las superficies opuestas y, en consecuencia, no hay tensión tangencial en la interfaz de contacto.
• Si se aumentan simultáneamente la aproximación en dirección normal y el desplazamiento tangencial ("compresión oblicua"), entonces se puede lograr una situación con tensión tangencial pero sin deslizamiento local. ^[2]

Esto demuestra que el estado en la interfaz de contacto no sólo depende de las posiciones relativas de los dos cuerpos, sino también de su historial de movimiento. Otro ejemplo de esto ocurre si la esfera vuelve a su posición original. Inicialmente no hubo tensión tangencial en la interfaz de contacto. Después del cambio inicial se ha producido el microdeslizamiento. Este microdeslizamiento no se deshace por completo al retroceder. Así, en la situación final, las tensiones tangenciales permanecen en la interfaz, en lo que parece una configuración idéntica a la original.

El efecto de la fricción sobre los contactos dinámicos (impactos) se analiza detalladamente en ^[14]

Solución de problemas de contacto rodante.

Contacto rodante entre un cilindro y un avión. Las partículas se mueven a través del área de contacto de derecha a izquierda, siendo tensadas cada vez más hasta que comienza el deslizamiento local.

Los problemas de contacto rodante son problemas dinámicos en los que los cuerpos en contacto se mueven continuamente entre sí. Una diferencia con los problemas de contacto deslizante dinámico es que hay más variedad en el estado de las diferentes partículas superficiales. Mientras que en un problema de deslizamiento la zona de contacto está formada continuamente por más o menos las mismas partículas, en un problema de contacto rodante las partículas entran y salen de la zona de contacto incesantemente. Además, en un problema de deslizamiento, las partículas de la superficie en la zona de contacto están todas sujetas más o menos al mismo desplazamiento tangencial en todas partes, mientras que en un problema de rodadura las partículas de la superficie se esfuerzan de maneras bastante diferentes. Están libres de tensión al entrar en la zona de contacto, luego se adhieren a una partícula de la superficie opuesta, son tensos por la diferencia general de movimiento entre los dos cuerpos, hasta que se excede el límite de tracción local y se produce el deslizamiento local. Este proceso está en diferentes etapas para diferentes partes del área de contacto.

Si el movimiento general de los cuerpos es constante, entonces se puede alcanzar un estado estacionario general. Aquí el estado de cada partícula de la superficie varía con el tiempo, pero la distribución general puede ser constante. Esto se formaliza mediante el uso de un sistema de coordenadas que se mueve junto con la zona de contacto.

Cilindro rodando sobre un plano, la solución Carter-Fromm (2D)

Considere un cilindro que rueda sobre un plano (medio espacio) en condiciones estacionarias, con una fuga longitudinal independiente del tiempo . (Relativamente) lejos de los extremos de los cilindros se produce una situación de deformación plana y el problema es bidimensional. ${\displaystyle \xi }$

Si el cilindro y el plano están hechos del mismo material, entonces el problema de contacto normal no se ve afectado por el esfuerzo cortante. El área de contacto es una tira y la presión se describe mediante la solución (2D) Hertz. ${\displaystyle x\in [-a,a]}$

${\displaystyle {\begin{aligned}p_{n}(x)&={\frac {p_{0}}{a}}{\sqrt {a^{2}-x^{2}}}&|x|&\leq a&a^{2}&={\frac {4F_{n}R}{\pi E^{*}}}\\p_{0}&={\frac {2F_{n}}{\pi a}}&&&E^{*}&={\frac {E}{2\left(1-\nu ^{2}\right)}}&\end{aligned}}}$

La distribución del esfuerzo cortante se describe mediante la solución de Carter-Fromm. Consiste en un área de adhesión en el borde de ataque del área de contacto y un área de deslizamiento en el borde de salida. Se indica la longitud del área de adhesión . Además, la coordenada de adhesión se introduce mediante . En caso de una fuerza positiva (fuga negativa ) es: ${\displaystyle 2a'}$ ${\displaystyle x'=x+a-a'}$ ${\displaystyle F_{x}>0}$ ${\displaystyle \xi <0}$

${\displaystyle {\begin{aligned}p_{x}(x)&=0&|&x|\geq a\\p_{x}(x)&={\frac {\mu p_{0}}{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a-2a'\leq {}&x\leq a\\p_{x}(x)&=\mu p_{n}(x)&&x\leq a-2a'\end{aligned}}}$

El tamaño del área de adherencia depende de la fuga, el radio de la rueda y el coeficiente de fricción.

${\displaystyle {\begin{aligned}a'&=a{\sqrt {1-{\frac {|F_{x}|}{\mu F_{n}}}}},&{\mbox{for }}|F_{x}|\leq \mu F_{n}\\\xi &=-\operatorname {sign} (F_{x})\,{\frac {\mu (a-a')}{R}},&{\mbox{i.e. }}|\xi |\leq {\frac {\mu a}{R}}\\F_{x}&=-\operatorname {sign} (\xi )\,\mu F_{n}\left(1-\left(1+{\frac {R|\xi |}{\mu a}}\right)^{2}\right)\end{aligned}}}$

Para fugas más grandes , tales como que se produzca un deslizamiento total. ${\displaystyle a'=0}$

Enfoques basados ​​en el medio espacio

Al considerar problemas de contacto en escalas espaciales intermedias, se ignoran las faltas de homogeneidad del material a pequeña escala y la rugosidad de la superficie. Se considera que los cuerpos están formados por superficies lisas y materiales homogéneos. Se adopta un enfoque continuo donde las tensiones, deformaciones y desplazamientos se describen mediante funciones continuas (por partes).

El enfoque del medio espacio es una estrategia de solución elegante para los llamados problemas de contacto de "bordes lisos" o "concentrados".

1. Si un cuerpo elástico masivo se carga en una pequeña sección de su superficie, entonces las tensiones elásticas se atenúan proporcionalmente y los desplazamientos elásticos cuando uno se aleja de esta área de superficie. ${\displaystyle 1/distance^{2}}$ ${\displaystyle 1/distance}$
2. Si un cuerpo no tiene esquinas afiladas en o cerca de la región de contacto, entonces su respuesta a una carga superficial puede aproximarse bien mediante la respuesta de un semiespacio elástico (por ejemplo, todos los puntos con ). ${\displaystyle (x,y,z)^{\mathsf {T}}\in \mathbb {R} ^{3}\,\!}$ ${\displaystyle z>0\,\!}$
3. El problema del semiespacio elástico se resuelve analíticamente, ver solución de Boussinesq-Cerruti .
4. Debido a la linealidad de este enfoque, se pueden superponer múltiples soluciones parciales.

Utilizando la solución fundamental para el medio espacio, el problema de contacto 3D completo se reduce a un problema 2D para las superficies delimitadoras de los cuerpos.

Se produce una simplificación adicional si los dos cuerpos son "geométrica y elásticamente iguales". En general, la tensión dentro de un cuerpo en una dirección induce también desplazamientos en direcciones perpendiculares. En consecuencia, existe una interacción entre la tensión normal y los desplazamientos tangenciales en el problema de contacto, y una interacción entre la tensión tangencial y los desplazamientos normales. Pero si la tensión normal en la interfaz de contacto induce los mismos desplazamientos tangenciales en ambos cuerpos en contacto, entonces no hay desplazamiento tangencial relativo de las dos superficies. En ese caso, los problemas de contacto normal y tangencial están desacoplados. Si este es el caso entonces los dos cuerpos se llaman casi idénticos . Esto sucede, por ejemplo, si los cuerpos son simétricos respecto al plano de contacto y tienen las mismas constantes elásticas.

Las soluciones clásicas basadas en el enfoque del medio espacio son:

1. Hertz resolvió el problema del contacto en ausencia de fricción, para una geometría simple (superficies curvas con radios de curvatura constantes).
2. Carter consideró el contacto rodante entre un cilindro y un plano, como se describió anteriormente. Se proporciona una solución analítica completa para la tracción tangencial.
3. Cattaneo consideró la compresión y el desplazamiento de dos esferas, como se describió anteriormente. Tenga en cuenta que esta solución analítica es aproximada. En realidad se producen pequeñas tracciones tangenciales que se ignoran. ${\displaystyle p_{y}}$

Ver también

• Ferrocarril de adhesión  : ferrocarril que depende de la tracción de adhesión para mover un tren.
• Cojinete  : mecanismo para restringir el movimiento relativo al movimiento deseado y reducir las fricciones.
• Mecánica de contacto  – Estudio de la deformación de sólidos que se tocan entre sí.
• Elasticidad (lineal)  : propiedad física cuando los materiales u objetos vuelven a su forma original después de la deformación.
• Cemento modificado energéticamente  : clase de cementos procesados ​​mecánicamente para transformar la reactividad.
• Fricción  : fuerza que resiste el movimiento deslizante.
• Accionamiento por fricción  : transmisión de potencia mecánica por fricción entre componentes.
• Lubricación  : presencia de un material para reducir la fricción entre dos superficies.
• Metalurgia  : campo de la ciencia que estudia el comportamiento físico y químico de los metales.
• Sistema multicuerpo  : herramienta para estudiar el comportamiento dinámico de cuerpos rígidos o flexibles interconectados
• Plasticidad  : deformación irreversible de un material sólido en respuesta a fuerzas aplicadas.
• Laminado (metalurgia)  – Proceso de conformado de metales
• Mecánica de sólidos  : rama de la mecánica que se ocupa de los materiales sólidos y sus comportamientos.
• CVT toroidal o de rodillos (Extroid CVT)  : tecnología de transmisión automotriz
• Tribología  : ciencia e ingeniería de superficies que interactúan en movimiento relativo.
• Dinámica del vehículo  : el estudio de los cambios de movimiento del vehículo en respuesta a la interacción con las acciones del conductor, las condiciones de la carretera y otras condiciones ambientales.Pages displaying wikidata descriptions as a fallback
• Desgaste  : daño, eliminación gradual o deformación del material en superficies sólidas.

Referencias

1. Johnson, KL (1985). Contacta con Mecánica . Cambridge: Prensa de la Universidad de Cambridge.
2. Popov, VL (2010). Contacta con Mecánica y Fricción. Principios físicos y aplicaciones . Berlín: Springer-Verlag.
3. "Introducción a la Tribología - Fricción" . Consultado el 21 de diciembre de 2008 .
4. Hertz, Heinrich (1882). "Contacto entre cuerpos sólidos elásticos". Journal für die Reine und Angewandte Mathematik . 92 .
5. Knothe, K. (2008). "Historia de la mecánica de contacto rueda/carril: de Redtenbacher a Kalker". Dinámica del sistema del vehículo . 46 (1–2): 9–26. doi :10.1080/00423110701586469.
6. Kalker, Joost J. (1967). Sobre el contacto rodante de dos cuerpos elásticos en presencia de fricción seca . Universidad Tecnológica de Delft.
7. Pacejka, Hans (2002). Dinámica de neumáticos y vehículos . Oxford: Butterworth-Heinemann.
8. Laursen, TA, 2002, Mecánica de impacto y contacto computacional, fundamentos del modelado de fenómenos interfaciales en análisis de elementos finitos no lineales , Springer, Berlín
9. Wriggers, P., 2006, Mecánica de contacto computacional, 2ª ed. , Springer, Heidelberg
10. Kalker, JJ (1990). Cuerpos Elásticos Tridimensionales en Contacto Rodante . Dordrecht: Editores académicos de Kluwer.
11. B. Jacobsen y JJ Kalker, ed. (2000). Fenómenos de contacto rodante . Viena Nueva York: Springer-Verlag.
12. Konyukhov, Alexander (1 de abril de 2015). "Contacto de cuerdas y superficies rugosas ortotrópicas". Revista de Matemáticas y Mecánica Aplicadas . 95 (4): 406–423. Código Bib : 2015ZaMM...95..406K. doi : 10.1002/zamm.201300129 . ISSN  1521-4001.
13. Konyukhov A., Izi R. "Introducción a la mecánica de contacto computacional: un enfoque geométrico". Wiley.
14. Willert, Emanuel (2020). Stoßprobleme in Physik, Technik und Medizin: Grundlagen und Anwendungen (en alemán). Springer Vieweg.

enlaces externos

• [1] ^{[ enlace muerto permanente ]} Biografía del Prof.dr.ir. JJ Kalker (Universidad Tecnológica de Delft).
• [2] Software CONTACT hertziano/no hertziano de Kalker.