En geografía , la latitud es una coordenada que especifica la posición norte - sur de un punto en la superficie de la Tierra u otro cuerpo celeste. La latitud se expresa como un ángulo que va desde -90° en el polo sur hasta 90° en el polo norte, con 0° en el ecuador . Las líneas de latitud constante , o paralelos , corren de este a oeste como círculos paralelos al ecuador. La latitud y la longitud se utilizan juntas como un par de coordenadas para especificar una ubicación en la superficie de la Tierra.
Por sí solo, el término "latitud" normalmente se refiere a la latitud geodésica tal como se define a continuación. Brevemente, la latitud geodésica de un punto es el ángulo formado entre el vector perpendicular (o normal ) a la superficie elipsoidal desde el punto y el plano del ecuador .
En las definiciones de latitud y longitud se emplean dos niveles de abstracción. En el primer paso, la superficie física se modela mediante el geoide , una superficie que se aproxima al nivel medio del mar sobre los océanos y su continuación bajo las masas terrestres. El segundo paso es aproximar el geoide mediante una superficie de referencia matemáticamente más simple. La opción más simple para la superficie de referencia es una esfera , pero el geoide se modela con mayor precisión mediante un elipsoide de revolución . Las definiciones de latitud y longitud en dichas superficies de referencia se detallan en las siguientes secciones. Las líneas de latitud y longitud constantes constituyen juntas una retícula en la superficie de referencia. La latitud de un punto en la superficie real es la del punto correspondiente en la superficie de referencia, siendo la correspondencia a lo largo de la normal a la superficie de referencia, que pasa por el punto en la superficie física. La latitud y la longitud junto con alguna especificación de altura constituyen un sistema de coordenadas geográficas según se define en la especificación de la norma ISO 19111. [1]
Dado que existen muchos elipsoides de referencia diferentes , la latitud precisa de una característica en la superficie no es única: esto se enfatiza en la norma ISO que establece que "sin la especificación completa del sistema de referencia de coordenadas, las coordenadas (es decir, latitud y longitud) son ambiguas en el mejor de los casos y sin sentido en el peor". Esto es de gran importancia en aplicaciones precisas, como un Sistema de Posicionamiento Global (GPS), pero en el uso común, donde no se requiere alta precisión, el elipsoide de referencia no suele indicarse.
En los textos en inglés, el ángulo de latitud, definido a continuación, se suele indicar con la letra griega minúscula phi ( ϕ o φ ). Se mide en grados , minutos y segundos o grados decimales , al norte o al sur del ecuador. Para fines de navegación, las posiciones se dan en grados y minutos decimales. Por ejemplo, el faro de The Needles está a 50°39.734′ N 001°35.500′ O. [2]
Este artículo se refiere a los sistemas de coordenadas de la Tierra: puede adaptarse para cubrir la Luna, los planetas y otros objetos celestes ( latitud planetográfica ).
Para una breve historia, consulte Historia de la latitud .
En la navegación astronómica , la latitud se determina con el método de la altitud meridiana . Para una medición más precisa de la latitud es necesario conocer el campo gravitatorio de la Tierra, ya sea para instalar teodolitos o para determinar las órbitas de los satélites GPS. El estudio de la figura de la Tierra junto con su campo gravitatorio es la ciencia de la geodesia .
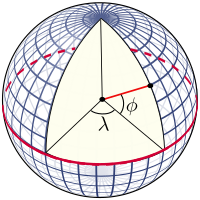
La retícula está formada por las líneas de latitud y longitud constantes, que se construyen con referencia al eje de rotación de la Tierra. Los puntos de referencia primarios son los polos donde el eje de rotación de la Tierra interseca la superficie de referencia. Los planos que contienen el eje de rotación intersecan la superficie en los meridianos ; y el ángulo entre cualquier plano meridiano y el que pasa por Greenwich (el Meridiano de Greenwich) define la longitud: los meridianos son líneas de longitud constante. El plano que pasa por el centro de la Tierra y es perpendicular al eje de rotación interseca la superficie en un gran círculo llamado Ecuador . Los planos paralelos al plano ecuatorial intersecan la superficie en círculos de latitud constante; estos son los paralelos. El Ecuador tiene una latitud de 0°, el Polo Norte tiene una latitud de 90° Norte (escrito 90° N o +90°), y el Polo Sur tiene una latitud de 90° Sur (escrito 90° S o −90°). La latitud de un punto arbitrario es el ángulo entre el plano ecuatorial y la normal a la superficie en ese punto: la normal a la superficie de la esfera está a lo largo del vector radial.
La latitud, tal como se define de esta manera para la esfera, a menudo se denomina latitud esférica, para evitar ambigüedades con la latitud geodésica y las latitudes auxiliares definidas en secciones posteriores de este artículo.
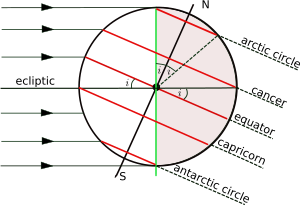
Además del ecuador, hay otros cuatro paralelos importantes:
El plano de la órbita de la Tierra alrededor del Sol se llama eclíptica y el plano perpendicular al eje de rotación de la Tierra es el plano ecuatorial. El ángulo entre la eclíptica y el plano ecuatorial se llama de diversas formas inclinación axial, oblicuidad o inclinación de la eclíptica y se denota convencionalmente por i . La latitud de los círculos tropicales es igual a i y la latitud de los círculos polares es su complemento (90° - i ). El eje de rotación varía lentamente con el tiempo y los valores dados aquí son los de la época actual . La variación temporal se analiza con más detalle en el artículo sobre la inclinación axial . [a]
La figura muestra la geometría de una sección transversal del plano perpendicular a la eclíptica y que pasa por los centros de la Tierra y el Sol en el solsticio de diciembre , cuando el Sol se encuentra en lo alto en algún punto del Trópico de Capricornio . Las latitudes polares sur por debajo del Círculo Antártico son de día, mientras que las latitudes polares norte por encima del Círculo Polar Ártico son de noche. La situación se invierte en el solsticio de junio, cuando el Sol se encuentra en lo alto en el Trópico de Cáncer. Solo en latitudes entre los dos trópicos es posible que el Sol se encuentre directamente en lo alto (en el cenit ).
En las proyecciones cartográficas no existe una regla universal sobre cómo deben aparecer los meridianos y los paralelos. Los ejemplos siguientes muestran los paralelos nombrados (como líneas rojas) en la proyección Mercator, que se utiliza habitualmente , y en la proyección Mercator transversal . En la primera, los paralelos son horizontales y los meridianos son verticales, mientras que en la segunda no existe una relación exacta entre los paralelos y los meridianos y la horizontal y la vertical: ambas son curvas complicadas.
En 1687, Isaac Newton publicó los Philosophiæ Naturalis Principia Mathematica , en los que demostró que un cuerpo fluido autogravitatorio giratorio en equilibrio adopta la forma de un elipsoide achatado . [3] (En este artículo se utiliza el término elipsoide en lugar del término más antiguo esferoide ). El resultado de Newton fue confirmado por mediciones geodésicas en el siglo XVIII. (Véase Arco meridiano ). Un elipsoide achatado es la superficie tridimensional generada por la rotación de una elipse sobre su eje más corto (eje menor). "Elipsoide achatado de revolución" se abrevia como "elipsoide" en el resto de este artículo. (Los elipsoides que no tienen un eje de simetría se denominan triaxiales ).
En la historia de la geodesia se han utilizado muchos elipsoides de referencia diferentes . En la época anterior a los satélites, se idearon para dar un buen ajuste al geoide sobre el área limitada de un estudio, pero con la llegada del GPS , se ha vuelto natural utilizar elipsoides de referencia (como WGS84 ) con el centro en el centro de masa de la Tierra y el eje menor alineado con el eje de rotación de la Tierra. Estos elipsoides geocéntricos suelen estar a 100 m (330 pies) del geoide. Dado que la latitud se define con respecto a un elipsoide, la posición de un punto dado es diferente en cada elipsoide: no se puede especificar exactamente la latitud y la longitud de una característica geográfica sin especificar el elipsoide utilizado. Muchos mapas mantenidos por agencias nacionales se basan en elipsoides más antiguos, por lo que se debe saber cómo se transforman los valores de latitud y longitud de un elipsoide a otro. Los dispositivos GPS incluyen software para realizar transformaciones de datos que vinculan WGS84 con el elipsoide de referencia local con su cuadrícula asociada.
La forma de un elipsoide de revolución está determinada por la forma de la elipse que gira sobre su eje menor (el más corto). Se requieren dos parámetros. Uno es invariablemente el radio ecuatorial, que es el semieje mayor , a . El otro parámetro suele ser (1) el radio polar o semieje menor , b ; o (2) el (primer) aplanamiento , f ; o (3) la excentricidad , e . Estos parámetros no son independientes: están relacionados por
Muchos otros parámetros (ver elipse , elipsoide ) aparecen en el estudio de la geodesia, la geofísica y las proyecciones cartográficas, pero todos ellos pueden expresarse en términos de uno o dos miembros del conjunto a , b , f y e . Tanto f como e son pequeños y a menudo aparecen en expansiones en serie en los cálculos; son del orden1/298 y 0,0818 respectivamente. Los valores para varios elipsoides se dan en la Figura de la Tierra . Los elipsoides de referencia suelen definirse por el semieje mayor y el aplanamiento inverso , 1/F . Por ejemplo, los valores que definen el elipsoide WGS84 , utilizado por todos los dispositivos GPS, son [4]
de donde se derivan
La diferencia entre los semiejes mayor y menor es de unos 21 km (13 millas) y, como fracción del semieje mayor, equivale al aplanamiento; en un monitor de ordenador, el elipsoide podría tener un tamaño de 300 por 299 píxeles. Esto apenas se distinguiría de una esfera de 300 por 300 píxeles, por lo que las ilustraciones suelen exagerar el aplanamiento.
La retícula del elipsoide se construye exactamente de la misma manera que en la esfera. La normal en un punto de la superficie de un elipsoide no pasa por el centro, excepto en los puntos del ecuador o de los polos, pero la definición de latitud permanece inalterada como el ángulo entre la normal y el plano ecuatorial. La terminología de latitud debe ser más precisa distinguiendo:
La latitud geográfica debe utilizarse con cuidado, ya que algunos autores la utilizan como sinónimo de latitud geodésica, mientras que otros la utilizan como alternativa a la latitud astronómica. "Latitud" (sin calificativos) normalmente debería hacer referencia a la latitud geodésica.
La importancia de especificar el datum de referencia se puede ilustrar con un ejemplo sencillo. En el elipsoide de referencia de WGS84, el centro de la Torre Eiffel tiene una latitud geodésica de 48° 51′ 29″ N, o 48,8583° N y una longitud de 2° 17′ 40″ E o 2,2944° E. Las mismas coordenadas en el datum ED50 definen un punto en el terreno que está a 140 metros (460 pies) de distancia de la torre. [ cita requerida ] Una búsqueda en la web puede producir varios valores diferentes para la latitud de la torre; el elipsoide de referencia rara vez se especifica.
La longitud de un grado de latitud depende de la figura de la Tierra asumida.
En la esfera, la normal pasa por el centro y la latitud ( ϕ ) es, por tanto, igual al ángulo subtendido en el centro por el arco meridiano desde el ecuador hasta el punto en cuestión. Si la distancia meridiana se denota por m ( ϕ ) , entonces
donde R denota el radio medio de la Tierra. R es igual a 6.371 km o 3.959 millas. No es apropiada una precisión mayor para R ya que los resultados de mayor precisión requieren un modelo de elipsoide. Con este valor para R, la longitud del meridiano de 1 grado de latitud en la esfera es 111,2 km (69,1 millas terrestres) (60,0 millas náuticas). La longitud de 1 minuto de latitud es 1,853 km (1,151 millas terrestres) (1,00 millas náuticas), mientras que la longitud de 1 segundo de latitud es 30,8 m o 101 pies (véase milla náutica ).
En los textos de arco meridiano y estándar [5] [6] [7] se muestra que la distancia a lo largo de un meridiano desde la latitud ϕ hasta el ecuador está dada por ( ϕ en radianes)
donde M ( ϕ ) es el radio de curvatura meridional .
La distancia del cuarto meridiano desde el ecuador hasta el polo es
Para WGS84 esta distancia es10 001 .965 729 kilómetros .
La evaluación de la integral de la distancia meridiana es fundamental para muchos estudios en geodesia y proyección de mapas. Se puede evaluar expandiendo la integral por la serie binomial e integrando término por término: véase Arco meridiano para más detalles. La longitud del arco meridiano entre dos latitudes dadas se obtiene reemplazando los límites de la integral por las latitudes en cuestión. La longitud de un arco meridiano pequeño se obtiene mediante [6] [7]
Cuando la diferencia de latitud es de 1 grado, corresponde a π/180 radianes, la distancia del arco es aproximadamente
La distancia en metros (correcta a 0,01 metros) entre las latitudes − 0,5 grados y + 0,5 grados en el esferoide WGS84 es
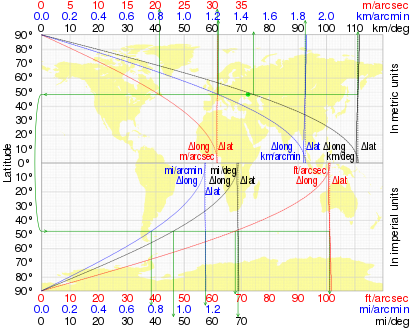
La variación de esta distancia con la latitud (en WGS84 ) se muestra en la tabla junto con la longitud de un grado de longitud (distancia este-oeste):
La Agencia Nacional de Inteligencia Geoespacial (NGA) del Gobierno de los EE. UU. proporciona una calculadora para cualquier latitud. [8]
El siguiente gráfico ilustra la variación de un grado de latitud y un grado de longitud con la latitud.
Hay seis latitudes auxiliares que tienen aplicaciones en problemas especiales de geodesia, geofísica y teoría de proyecciones cartográficas:
Las definiciones que se dan en esta sección se refieren a ubicaciones en el elipsoide de referencia, pero las dos primeras latitudes auxiliares, como la latitud geodésica, se pueden ampliar para definir un sistema de coordenadas geográficas tridimensional , como se explica a continuación. Las latitudes restantes no se utilizan de esta manera; se utilizan solo como construcciones intermedias en proyecciones cartográficas del elipsoide de referencia al plano o en cálculos de geodésicas en el elipsoide. Sus valores numéricos no son de interés. Por ejemplo, nadie necesitaría calcular la latitud auténtica de la Torre Eiffel.
Las expresiones que aparecen a continuación indican las latitudes auxiliares en términos de la latitud geodésica, el semieje mayor, a , y la excentricidad, e . (Para las inversas, véase más abajo). Las formas que se dan son, aparte de las variantes de notación, las que aparecen en la referencia estándar para proyecciones cartográficas, a saber, "Map projections: a working manual" de JP Snyder. [9] Se pueden encontrar derivaciones de estas expresiones en Adams [10] y en las publicaciones en línea de Osborne [6] y Rapp. [7]
La latitud geocéntrica es el ángulo entre el plano ecuatorial y el radio desde el centro hasta un punto de interés.
Cuando el punto está en la superficie del elipsoide, la relación entre la latitud geocéntrica ( θ ) y la latitud geodésica ( ϕ ) es:
Para los puntos que no están en la superficie del elipsoide, la relación implica adicionalmente la altura elipsoidal h :
donde N es el radio de curvatura vertical principal. Las latitudes geodésicas y geocéntricas son iguales en el ecuador y en los polos, pero en otras latitudes difieren en unos pocos minutos de arco. Si tomamos el valor de la excentricidad al cuadrado como 0,0067 (depende de la elección del elipsoide), la diferencia máxima de puede demostrarse que es de unos 11,5 minutos de arco en una latitud geodésica de aproximadamente 45° 6′. [b]
La latitud paramétrica o latitud reducida , β , se define por el radio trazado desde el centro del elipsoide hasta ese punto Q en la esfera circundante (de radio a ) que es la proyección paralela al eje de la Tierra de un punto P en el elipsoide en latitud ϕ . Fue introducida por Legendre [11] y Bessel [12] quienes resolvieron problemas para geodésicas en el elipsoide transformándolos en un problema equivalente para geodésicas esféricas utilizando esta latitud más pequeña. La notación de Bessel, u ( ϕ ) , también se utiliza en la literatura actual. La latitud paramétrica está relacionada con la latitud geodésica por: [6] [7]
El nombre alternativo surge de la parametrización de la ecuación de la elipse que describe una sección meridiana. En términos de coordenadas cartesianas p , la distancia desde el eje menor, y z , la distancia sobre el plano ecuatorial, la ecuación de la elipse es:
Las coordenadas cartesianas del punto están parametrizadas por
Cayley sugirió el término latitud paramétrica debido a la forma de estas ecuaciones. [13]
La latitud paramétrica no se utiliza en la teoría de proyecciones cartográficas. Su aplicación más importante es en la teoría de geodésicas elipsoidales ( Vincenty , Karney [14] ).
La latitud rectificadora , μ , es la distancia del meridiano escalada de modo que su valor en los polos sea igual a 90 grados oπ/2 radianes:
donde la distancia meridiana desde el ecuador hasta una latitud ϕ es (ver Arco meridiano )
y la longitud del cuadrante meridiano desde el ecuador hasta el polo (la distancia polar ) es
Utilizando la latitud rectificadora para definir una latitud en una esfera de radio
define una proyección desde el elipsoide a la esfera de manera que todos los meridianos tengan longitud verdadera y escala uniforme. La esfera puede entonces proyectarse al plano con una proyección equirectangular para dar una proyección doble desde el elipsoide al plano de manera que todos los meridianos tengan longitud verdadera y escala meridiana uniforme. Un ejemplo del uso de la latitud rectificadora es la proyección cónica equidistante . (Snyder, Sección 16). [9] La latitud rectificadora también es de gran importancia en la construcción de la proyección transversal de Mercator .
La latitud autálica (del griego "misma área"), ξ , da una proyección de área igual a una esfera.
dónde
y
y el radio de la esfera se toma como
Un ejemplo del uso de la latitud autálica es la proyección cónica de áreas iguales de Albers . [9] : §14
La latitud conforme , χ , proporciona una transformación que preserva el ángulo ( conforme ) a la esfera. [15]
donde gd( x ) es la función de Gudermann . (Véase también proyección de Mercator .)
La latitud conforme define una transformación del elipsoide a una esfera de radio arbitrario , de modo que el ángulo de intersección entre dos líneas cualesquiera del elipsoide sea el mismo que el ángulo correspondiente en la esfera (de modo que se conserve bien la forma de los elementos pequeños ). Otra transformación conforme de la esfera al plano da una proyección doble conforme del elipsoide al plano. Esta no es la única forma de generar una proyección conforme de este tipo. Por ejemplo, la versión "exacta" de la proyección transversal de Mercator sobre el elipsoide no es una proyección doble (no obstante, implica una generalización de la latitud conforme al plano complejo).
La latitud isométrica , ψ , se utiliza en el desarrollo de las versiones elipsoidales de la proyección normal de Mercator y la proyección transversal de Mercator . El nombre "isométrica" surge del hecho de que en cualquier punto del elipsoide incrementos iguales de ψ y longitud λ dan lugar a desplazamientos de distancia iguales a lo largo de los meridianos y paralelos respectivamente. La retícula definida por las líneas de constante ψ y constante λ divide la superficie del elipsoide en una malla de cuadrados (de tamaño variable). La latitud isométrica es cero en el ecuador pero diverge rápidamente de la latitud geodésica, tendiendo al infinito en los polos. La notación convencional se da en Snyder (página 15): [9]
Para la proyección normal de Mercator (sobre el elipsoide), esta función define el espaciamiento de los paralelos: si la longitud del ecuador en la proyección es E (unidades de longitud o píxeles), entonces la distancia, y , de un paralelo de latitud ϕ desde el ecuador es
La latitud isométrica ψ está estrechamente relacionada con la latitud conforme χ :
Las fórmulas de las secciones anteriores dan la latitud auxiliar en términos de la latitud geodésica. Las expresiones para las latitudes geocéntrica y paramétrica pueden invertirse directamente, pero esto es imposible en los cuatro casos restantes: las latitudes rectificadoras, autálicas, conformes e isométricas. Hay dos métodos para proceder.
El gráfico de la derecha muestra la diferencia entre la latitud geodésica y las latitudes auxiliares distintas de la latitud isométrica (que diverge hasta el infinito en los polos) para el caso del elipsoide WGS84. Las diferencias que se muestran en el gráfico se expresan en minutos de arco. En el hemisferio norte (latitudes positivas), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ ; en el hemisferio sur (latitudes negativas), las desigualdades se invierten, con igualdad en el ecuador y los polos. Aunque el gráfico parece simétrico alrededor de 45°, los mínimos de las curvas en realidad se encuentran entre 45° 2′ y 45° 6′. En la tabla siguiente se dan algunos puntos de datos representativos. Las latitudes conformes y geocéntricas son casi indistinguibles, un hecho que se explotó en la época de las calculadoras manuales para acelerar la construcción de proyecciones cartográficas. [9] : 108
Para el primer orden en el aplanamiento f , las latitudes auxiliares se pueden expresar como ζ = ϕ − Cf sen 2 ϕ donde la constante C toma los valores [ 1 ⁄ 2 , 2 ⁄ 3 , 3 ⁄ 4 , 1, 1] para ζ = [ β , ξ , μ , χ , θ ].
La latitud geodésica, o cualquiera de las latitudes auxiliares definidas en el elipsoide de referencia, constituye junto con la longitud un sistema de coordenadas bidimensional en dicho elipsoide. Para definir la posición de un punto arbitrario es necesario extender dicho sistema de coordenadas a tres dimensiones. De esta manera se utilizan tres latitudes: la latitud geodésica, la latitud geocéntrica y la latitud paramétrica, que se utilizan en coordenadas geodésicas, coordenadas polares esféricas y coordenadas elipsoidales respectivamente.
En un punto arbitrario P, considere la línea PN que es normal al elipsoide de referencia. Las coordenadas geodésicas P( ɸ , λ , h ) son la latitud y longitud del punto N en el elipsoide y la distancia PN . Esta altura difiere de la altura sobre el geoide o una altura de referencia como la que se encuentra sobre el nivel medio del mar en una ubicación específica. La dirección de PN también diferirá de la dirección de una plomada vertical. La relación de estas diferentes alturas requiere el conocimiento de la forma del geoide y también del campo gravitatorio de la Tierra.
La latitud geocéntrica θ es el complemento del ángulo polar o colatitud θ′ en coordenadas polares esféricas convencionales en las que las coordenadas de un punto son P( r , θ ′, λ ) donde r es la distancia de P al centro O , θ′ es el ángulo entre el radio vector y el eje polar y λ es la longitud. Dado que la normal en un punto general del elipsoide no pasa por el centro, es evidente que los puntos P' de la normal, que tienen todos la misma latitud geodésica, tendrán diferentes latitudes geocéntricas. Los sistemas de coordenadas polares esféricas se utilizan en el análisis del campo gravitatorio.
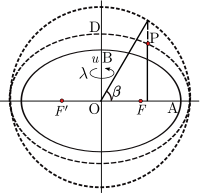
La latitud paramétrica también se puede extender a un sistema de coordenadas tridimensional. Para un punto P que no está en el elipsoide de referencia (semiejes OA y OB ) construya un elipsoide auxiliar que sea confocal (mismos focos F , F′ ) con el elipsoide de referencia: la condición necesaria es que el producto ae del semieje mayor y la excentricidad sea el mismo para ambos elipsoides. Sea u el semieje menor ( OD ) del elipsoide auxiliar. Además, sea β la latitud paramétrica de P en el elipsoide auxiliar. El conjunto ( u , β , λ ) define las coordenadas elipsoidales-armónicas [19] o simplemente coordenadas elipsoidales [5] : §4.2.2 (aunque ese término también se usa para referirse a las coordenadas geodésicas). Estas coordenadas son la elección natural en los modelos del campo de gravedad para un cuerpo elipsoidal giratorio. Lo anterior se aplica a un elipsoide biaxial (un esferoide, como en coordenadas esferoidales oblatas ); para una generalización, consulte coordenadas elipsoidales triaxiales .
Las relaciones entre los sistemas de coordenadas anteriores y las coordenadas cartesianas no se presentan aquí. La transformación entre coordenadas geodésicas y cartesianas se puede encontrar en conversión de coordenadas geográficas . La relación entre las coordenadas cartesianas y esféricas se da en sistema de coordenadas esféricas . La relación entre las coordenadas cartesianas y elipsoidales se analiza en Torge. [5]
La latitud astronómica ( Φ ) es el ángulo entre el plano ecuatorial y la dirección vertical verdadera en un punto de la superficie. La vertical verdadera, la dirección de una plomada , es también la dirección de la gravedad (la resultante de la aceleración gravitacional (basada en la masa) y la aceleración centrífuga ) en esa latitud. [5] La latitud astronómica se calcula a partir de los ángulos medidos entre el cenit y las estrellas cuya declinación se conoce con precisión.
En general, la vertical verdadera en un punto de la superficie no coincide exactamente ni con la normal al elipsoide de referencia ni con la normal al geoide. El geoide es una forma idealizada y teórica "a nivel medio del mar". Los puntos de la tierra no se encuentran exactamente sobre el geoide, y la vertical en un punto en un momento específico está influenciada por las fuerzas de marea que el geoide teórico promedia. El ángulo entre las normales astronómica y geodésica se denomina desviación vertical y suele ser de unos pocos segundos de arco, pero es importante en geodesia. [5] [20]
La latitud astronómica no debe confundirse con la declinación , la coordenada que los astrónomos utilizan de manera similar para especificar la posición angular de las estrellas al norte-sur del ecuador celeste (ver coordenadas ecuatoriales ), ni con la latitud eclíptica , la coordenada que los astrónomos utilizan para especificar la posición angular de las estrellas al norte-sur de la eclíptica (ver coordenadas eclípticas ).
Definiciones de Wikcionario
Medios de comunicación de Commons
Noticias de Wikinoticias
Citas de Wikiquote
Textos de Wikisource
Libros de texto de Wikilibros
Recursos de Wikiversidad
![{\displaystyle {\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{ 2}\phi }}-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e\sin \phi }{1+e\sin \phi }} \right)\\[2pt]&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }} +{\frac {1-e^{2}}{e}}\tanh ^{-1}(e\sin \phi )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b256b2b2f95ca49231dfb329dd724cdbd2de7d1)
![{\displaystyle {\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {1+\sin \phi }{1-\sin \phi } }\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{e}\right]^{\frac {1}{2}} -{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{\frac {e}{2}} \right]-{\frac {\pi }{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\nombredeloperador {gd} \left[ \operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi )\right]\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea5beec16e6a78772ab9d8ffd9123b9ae6e89e0)
![{\displaystyle {\begin{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}} \right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\& =\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e \tanh ^{-1}(e\sin \phi ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2999bd8461a831ee601ecad69062c5b30adec5f)
