Cuadrilátero tangencial

Polígono cuyos cuatro lados tocan un círculo

Un cuadrilátero tangencial con su círculo inscrito

En geometría euclidiana , un cuadrilátero tangencial (a veces simplemente cuadrilátero tangente ) o cuadrilátero circunscrito es un cuadrilátero convexo cuyos lados pueden ser todos tangentes a un solo círculo dentro del cuadrilátero. Este círculo se llama incírculo del cuadrilátero o su círculo inscrito, su centro es el incentro y su radio se llama inradio . Dado que estos cuadriláteros se pueden dibujar rodeando o circunscribiendo sus incírculos, también se han llamado cuadriláteros circunscribibles , cuadriláteros circunscriptos y cuadriláteros circunscriptibles . ^[1] Los cuadriláteros tangenciales son un caso especial de polígonos tangenciales .

Otros nombres menos utilizados para esta clase de cuadriláteros son cuadrilátero inscribible , cuadrilátero inscribible , cuadrilátero inscribible , cuadrilátero circuncíclico y cuadrilátero cocíclico . ^{[1] [2]} Debido al riesgo de confusión con un cuadrilátero que tiene un círculo circunscrito, que se llama cuadrilátero cíclico o cuadrilátero inscrito, es preferible no utilizar ninguno de los últimos cinco nombres. ^[1]

Todos los triángulos pueden tener un incírculo, pero no todos los cuadriláteros lo tienen. Un ejemplo de cuadrilátero que no puede ser tangencial es un rectángulo no cuadrado . La sección de caracterizaciones que se encuentra a continuación establece qué condiciones necesarias y suficientes debe satisfacer un cuadrilátero para poder tener un incírculo.

Casos especiales

Ejemplos de cuadriláteros tangenciales son las cometas , que incluyen a los rombos , que a su vez incluyen a los cuadrados . Las cometas son exactamente los cuadriláteros tangenciales que también son ortodiagonales . ^[3] Una cometa recta es una cometa con una circunferencia circunscrita . Si un cuadrilátero es a la vez tangencial y cíclico , se denomina cuadrilátero bicéntrico , y si es a la vez tangencial y trapezoide , se denomina trapezoide tangencial .

Caracterizaciones

En un cuadrilátero tangencial, las cuatro bisectrices de los ángulos se encuentran en el centro de la circunferencia inscrita. Por el contrario, un cuadrilátero convexo en el que las cuatro bisectrices de los ángulos se encuentran en un punto debe ser tangencial y el punto común es el incentro. ^[4]

Según el teorema de Pitot , los dos pares de lados opuestos de un cuadrilátero tangencial suman la misma longitud total, que es igual al semiperímetro s del cuadrilátero:

${\displaystyle a+c=b+d={\frac {a+b+c+d}{2}}=s.}$

Por el contrario, un cuadrilátero convexo en el que a + c = b + d debe ser tangencial. ^{[1] : p.65  [4]}

Si los lados opuestos de un cuadrilátero convexo ABCD (que no es un trapezoide ) se intersecan en E y F , entonces es tangencial si y solo si cualquiera de ^[4]

${\displaystyle \displaystyle BE+BF=DE+DF}$

o

${\displaystyle \displaystyle AE-EC=AF-FC:}$

Otra condición necesaria y suficiente es que un cuadrilátero convexo ABCD es tangente si y sólo si los círculos inscritos en los dos triángulos ABC y ADC son tangentes entre sí. ^{[1] : p.66}

La caracterización de los ángulos formados por la diagonal BD y los cuatro lados de un cuadrilátero ABCD se debe a Iosifescu, quien demostró en 1954 que un cuadrilátero convexo tiene un incírculo si y sólo si ^[5]

${\displaystyle \tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.}$

Un cuadrilátero tangente (en azul) con su círculo inscrito (línea discontinua) y los cuatro círculos tangentes externamente (en rojo), cada uno tangente a un lado dado y las extensiones de los lados adyacentes.

Además, un cuadrilátero convexo con lados sucesivos a , b , c , d es tangencial si y sólo si

${\displaystyle R_{a}R_{c}=R_{b}R_{d}}$

donde R _a , R _b , R _c , R _d son los radios en los círculos externamente tangentes a los lados a , b , c , d respectivamente y las extensiones de los dos lados adyacentes para cada lado. ^{[6] : p.72}

Se conocen varias caracterizaciones más en los cuatro subtriángulos formados por las diagonales.

Puntos de contacto y longitudes de tangentes

Un cuadrilátero tangencial (en azul) y su cuadrilátero de contacto (en verde) que une los cuatro puntos de contacto entre la circunferencia inscrita y los lados. También se muestran las cuerdas de tangencia que unen los puntos de contacto opuestos (en rojo) y las longitudes de las tangentes en los lados.

La circunferencia inscrita es tangente a cada lado en un punto de contacto . Estos cuatro puntos definen un nuevo cuadrilátero dentro del cuadrilátero inicial: el cuadrilátero de contacto, que es cíclico ya que está inscrito en la circunferencia inscrita del cuadrilátero inicial.

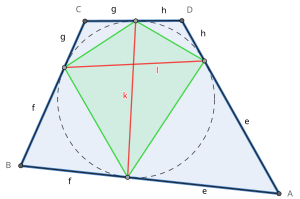
Las ocho longitudes de tangentes ( e , f , g , h en la figura de la derecha) de un cuadrilátero tangencial son los segmentos de línea que van desde un vértice hasta los puntos de contacto. Desde cada vértice hay dos longitudes de tangentes congruentes .

Las dos cuerdas tangentes ( k y l en la figura) de un cuadrilátero tangente son los segmentos de línea que unen los puntos de contacto en lados opuestos. También son las diagonales del cuadrilátero de contacto.

Área

Fórmulas no trigonométricas

El área K de un cuadrilátero tangencial está dada por

${\displaystyle \displaystyle K=r\cdot s,}$

donde s es el semiperímetro y r es el radio interno . Otra fórmula es ^[7]

${\displaystyle \displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-(ac-bd)^{2}}}}$

que da el área en términos de las diagonales p , q y los lados a , b , c , d del cuadrilátero tangencial.

El área también se puede expresar en términos de las cuatro longitudes tangentes. Si estas son e , f , g , h , entonces el cuadrilátero tangencial tiene el área ^[3]

${\displaystyle \displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.}$

Además, el área de un cuadrilátero tangencial se puede expresar en términos de los lados a, b, c, d y las longitudes tangentes sucesivas e, f, g, h como ^{[3] : p.128}

${\displaystyle K={\sqrt {abcd-(eg-fh)^{2}}}.}$

Dado que eg = fh si y solo si el cuadrilátero tangencial también es cíclico y, por lo tanto, bicéntrico, ^[8] esto demuestra que el área máxima ocurre si y solo si el cuadrilátero tangencial es bicéntrico. ${\displaystyle {\sqrt {abcd}}}$

Fórmulas trigonométricas

Una fórmula trigonométrica para el área en términos de los lados a , b , c , d y dos ángulos opuestos es ^{[7] [9] [10] [11]}

${\displaystyle \displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}}.}$

Para longitudes de lados dadas, el área es máxima cuando el cuadrilátero también es cíclico y, por lo tanto, un cuadrilátero bicéntrico . Entonces, dado que los ángulos opuestos son ángulos suplementarios , esto se puede demostrar de otra manera usando el cálculo . ^[12] ${\displaystyle K={\sqrt {abcd}}}$

Otra fórmula para el área de un cuadrilátero tangencial ABCD que involucra dos ángulos opuestos es ^{[10] : p.19}

${\displaystyle K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C}{2}}}$

donde I es el incentro.

De hecho, el área se puede expresar en términos de sólo dos lados adyacentes y dos ángulos opuestos como ^[7]

${\displaystyle K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.}$

Otra fórmula de área es ^[7]

${\displaystyle K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,}$

donde θ es cualquiera de los ángulos entre las diagonales. Esta fórmula no se puede utilizar cuando el cuadrilátero tangente es una cometa, ya que entonces θ es 90° y la función tangente no está definida.

Desigualdades

Como se señaló indirectamente anteriormente, el área de un cuadrilátero tangencial con lados a , b , c , d satisface

${\displaystyle K\leq {\sqrt {abcd}}}$

con igualdad si y sólo si es un cuadrilátero bicéntrico .

Según TA Ivanova (en 1976), el semiperímetro s de un cuadrilátero tangencial satisface

${\displaystyle s\geq 4r}$

donde r es el radio interno. Hay igualdad si y solo si el cuadrilátero es un cuadrado . ^[13] Esto significa que para el área K = rs , existe la desigualdad

${\displaystyle K\geq 4r^{2}}$

con igualdad si y sólo si el cuadrilátero tangencial es un cuadrado.

Propiedades de la partición

Cuadrilátero tangencial con radio interno r

Los cuatro segmentos de línea entre el centro del círculo inscrito y los puntos donde es tangente al cuadrilátero dividen el cuadrilátero en cuatro cometas rectas .

Si una línea corta un cuadrilátero tangencial en dos polígonos con áreas iguales y perímetros iguales , entonces esa línea pasa por el incentro . ^[4]

Inradio

El radio interno de un cuadrilátero tangencial con lados consecutivos a , b , c , d se da por ^[7]

${\displaystyle r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{b+d}}}$

donde K es el área del cuadrilátero y s es su semiperímetro. Para un cuadrilátero tangencial con lados dados, el radio interno es máximo cuando el cuadrilátero también es cíclico (y por lo tanto un cuadrilátero bicéntrico ).

En términos de las longitudes de las tangentes, el incírculo tiene radio ^{[8] : Lema 2  [14]}

${\displaystyle \displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.}$

El inradio también puede expresarse en términos de las distancias desde el incentro I a los vértices del cuadrilátero tangencial ABCD . Si u = AI , v = BI , x = CI e y = DI , entonces

${\displaystyle r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}}}$

donde . ^[15] ${\displaystyle \sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)}$

Si los círculos inscritos en los triángulos ABC , BCD , CDA y DAB tienen radios respectivamente, entonces el radio interno de un cuadrilátero tangencial ABCD está dado por ${\displaystyle r_{1},r_{2},r_{3},r_{4}}$

${\displaystyle r={\frac {G+{\sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}}}$

donde . ^[16] ${\displaystyle G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}}$

Fórmulas de ángulos

Si e , f , g y h son las longitudes tangentes desde los vértices A , B , C y D respectivamente hasta los puntos donde el incírculo es tangente a los lados de un cuadrilátero tangencial ABCD , entonces los ángulos del cuadrilátero se pueden calcular a partir de ^[3]

${\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},}$

${\displaystyle \sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},}$

${\displaystyle \sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},}$

${\displaystyle \sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.}$

El ángulo entre las cuerdas tangentes k y l está dado por ^[3]

${\displaystyle \sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.}$

Diagonales

Si e , f , g y h son las longitudes tangentes desde A , B , C y D respectivamente a los puntos donde el incírculo es tangente a los lados de un cuadrilátero tangencial ABCD , entonces las longitudes de las diagonales p = AC y q = BD son ^{[8] : Lema 3}

${\displaystyle \displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\Big (}(e+g)(f+h)+4fh{\Big )}}},}$

${\displaystyle \displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.}$

Acordes de tangencia

Si e , f , g y h son las longitudes tangentes de un cuadrilátero tangencial, entonces las longitudes de las cuerdas tangentes son ^[3]

${\displaystyle \displaystyle k={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},}$

${\displaystyle \displaystyle l={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}}$

donde la cuerda tangente de longitud k une los lados de longitudes a = e + f y c = g + h , y la de longitud l une los lados de longitudes b = f + g y d = h + e . La razón al cuadrado de las cuerdas tangentes satisface ^[3]

${\displaystyle {\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.}$

Los dos acordes de tangencia

• son perpendiculares si y sólo si el cuadrilátero tangencial también tiene un círculo circunscrito (es bicéntrico ). ^{[3] : p.124}
• tienen longitudes iguales si y sólo si el cuadrilátero tangencial es una cometa . ^{[17] : p.166}

La cuerda tangente entre los lados AB y CD en un cuadrilátero tangencial ABCD es más larga que la entre los lados BC y DA si y sólo si la bimediana entre los lados AB y CD es más corta que la entre los lados BC y DA . ^{[18] : p.162}

Si el cuadrilátero tangencial ABCD tiene puntos de tangencia W en AB e Y en CD , y si la cuerda de tangencia WY interseca la diagonal BD en M , entonces la relación de las longitudes de las tangentes es igual a la relación de los segmentos de la diagonal BD . ^[19] ${\displaystyle {\tfrac {BW}{DY}}}$ ${\displaystyle {\tfrac {BM}{DM}}}$

Puntos colineales

Construcción de la recta de Newton (en rojo) de un cuadrilátero tangencial (en azul), mostrando la alineación del incentro I , los puntos medios de las diagonales M ₁ y M ₂ y el punto medio M ₃ del segmento JK (en verde) que une la intersección de los lados opuestos.

Si M ₁ y M ₂ son los puntos medios de las diagonales AC y BD respectivamente en un cuadrilátero tangencial ABCD con incentro I , y si los pares de lados opuestos se encuentran en J y K siendo M ₃ el punto medio de JK , entonces los puntos M ₃ , M ₁ , I y M ₂ son colineales . ^{[4] : p.42} La línea que los contiene es la línea de Newton del cuadrilátero.

Si las extensiones de los lados opuestos en un cuadrilátero tangencial se intersecan en J y K , y las extensiones de los lados opuestos en su cuadrilátero de contacto se intersecan en L y M , entonces los cuatro puntos J , L , K y M son colineales. ^{[20] : Cor.3}

Un cuadrilátero tangencial está dividido en cuatro triángulos que se encuentran en su incentro I , sus ortocentros (en violeta) y la intersección de las diagonales P (en verde) son todos colineales.

Si el incírculo es tangente a los lados AB , BC , CD , DA en T ₁ , T ₂ , T ₃ , T ₄ respectivamente, y si N ₁ , N ₂ , N ₃ , N ₄ son los conjugados isotómicos de estos puntos con respecto a los lados correspondientes (es decir, AT ₁ = BN ₁ y así sucesivamente), entonces el punto de Nagel del cuadrilátero tangencial se define como la intersección de las líneas N ₁ N ₃ y N ₂ N ₄ . Ambas líneas dividen el perímetro del cuadrilátero en dos partes iguales. Más importante aún, el punto de Nagel N , el "centroide del área" G y el incentro I son colineales en este orden, y NG = 2 GI . Esta línea se llama línea de Nagel de un cuadrilátero tangencial. ^[21]

En un cuadrilátero tangencial ABCD con incentro I y cuyas diagonales se cortan en P , sean H _X , H _Y , H _Z , H _W los ortocentros de los triángulos AIB , BIC , CID , DIA . Entonces los puntos P , H _X , H _Y , H _Z , H _W son colineales. ^{[10] : p.28}

Rectas concurrentes y perpendiculares

Las dos diagonales y las dos cuerdas tangentes son concurrentes . ^{[11] [10] : p.11} Una forma de ver esto es como un caso límite del teorema de Brianchon , que establece que un hexágono cuyos lados son todos tangentes a una única sección cónica tiene tres diagonales que se encuentran en un punto. A partir de un cuadrilátero tangencial, se puede formar un hexágono con dos ángulos de 180°, colocando dos nuevos vértices en dos puntos opuestos de tangencia; los seis lados de este hexágono se encuentran en líneas tangentes al círculo inscrito, por lo que sus diagonales se encuentran en un punto. Pero dos de estas diagonales son las mismas que las diagonales del cuadrilátero tangencial, y la tercera diagonal del hexágono es la línea que pasa por dos puntos opuestos de tangencia. Repetir este mismo argumento con los otros dos puntos de tangencia completa la prueba del resultado.

Si las extensiones de los lados opuestos en un cuadrilátero tangencial se intersecan en J y K , y las diagonales se intersecan en P , entonces JK es perpendicular a la extensión de IP donde I es el incentro. ^{[20] : Cor.4}

Incentrado

El incentro de un cuadrilátero tangencial se encuentra en su línea de Newton (que conecta los puntos medios de las diagonales). ^{[22] : Teoría 3}

La relación de dos lados opuestos en un cuadrilátero tangencial se puede expresar en términos de las distancias entre el incentro I y los vértices según ^{[10] : p.15}

${\displaystyle {\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}}.}$

El producto de dos lados adyacentes en un cuadrilátero tangencial ABCD con incentro I satisface ^[23]

${\displaystyle AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.}$

Si I es el incentro de un cuadrilátero tangencial ABCD , entonces ^{[10] : p.16}

${\displaystyle IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.}$

El incentro I en un cuadrilátero tangencial ABCD coincide con el "centroide del vértice" del cuadrilátero si y sólo si ^{[10] : p.22}

${\displaystyle IA\cdot IC=IB\cdot ID.}$

Si M _p y M _q son los puntos medios de las diagonales AC y BD respectivamente en un cuadrilátero tangencial ABCD con incentro I , entonces ^{[10] : p.19  [24]}

${\displaystyle {\frac {IM_{p}}{IM_{q}}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}}$

donde e , f , g y h son las longitudes de las tangentes en A , B , C y D respectivamente. Combinando la primera igualdad con una propiedad anterior, el "centroide del vértice" del cuadrilátero tangencial coincide con el incentro si y solo si el incentro es el punto medio del segmento de línea que une los puntos medios de las diagonales.

Si se hace un enlace de cuatro barras en forma de cuadrilátero tangencial, entonces permanecerá tangencial sin importar cómo se flexione el enlace, siempre que el cuadrilátero permanezca convexo. ^{[25] [26]} (Así, por ejemplo, si un cuadrado se deforma en un rombo, permanece tangencial, aunque a un incírculo más pequeño). Si un lado se mantiene en una posición fija, entonces, a medida que el cuadrilátero se flexiona, el incentro traza un círculo de radio donde a, b, c, d son los lados en secuencia y s es el semiperímetro. ${\displaystyle {\sqrt {abcd}}/s}$

Caracterizaciones en los cuatro subtriángulos

Caracterización de Chao y Simeonov en términos de los radios de los círculos dentro de cada uno de los cuatro triángulos

En los triángulos no superpuestos APB , BPC , CPD , DPA formados por las diagonales de un cuadrilátero convexo ABCD , donde las diagonales se intersecan en P , existen las siguientes caracterizaciones de cuadriláteros tangenciales.

Sean r ₁ , r ₂ , r ₃ y r ₄ los radios de los círculos inscritos en los cuatro triángulos APB , BPC , CPD y DPA respectivamente. Chao y Simeonov demostraron que el cuadrilátero es tangencial si y solo si ^[27]

${\displaystyle {\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.}$

Esta caracterización ya había sido demostrada cinco años antes por Vaynshtejn. ^{[17] : p.169  [28]} En la solución de su problema, Vasilyev y Senderov dieron una caracterización similar. Si h ₁ , h ₂ , h ₃ y h ₄ denotan las alturas en los mismos cuatro triángulos (desde la intersección diagonal hasta los lados del cuadrilátero), entonces el cuadrilátero es tangencial si y solo si ^{[5] [28]}

${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}.}$

Otra caracterización similar se refiere a los radios excéntricos r _a , r _b , r _c y r _d en los mismos cuatro triángulos (los cuatro círculos excéntricos son tangentes a un lado del cuadrilátero y a las extensiones de sus diagonales). Un cuadrilátero es tangente si y sólo si ^{[1] : p.70}

${\displaystyle {\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1}{r_{d}}}.}$

Si R ₁ , R ₂ , R ₃ y R ₄ denotan los radios en los círculos circunscritos de los triángulos APB , BPC , CPD y DPA respectivamente, entonces el cuadrilátero ABCD es tangencial si y solo si ^{[29] : págs. 23–24}

${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}.}$

En 1996, Vaynshtejn fue probablemente el primero en demostrar otra hermosa caracterización de los cuadriláteros tangenciales, que luego apareció en varias revistas y sitios web. ^{[1] : pp. 72–73} Establece que cuando un cuadrilátero convexo se divide en cuatro triángulos no superpuestos por sus dos diagonales, entonces los incentros de los cuatro triángulos son concíclicos si y solo si el cuadrilátero es tangencial. De hecho, los incentros forman un cuadrilátero cíclico ortodiagonal . ^{[1] : p.74} Un resultado relacionado es que los incírculos se pueden intercambiar por los excírculos de los mismos triángulos (tangentes a los lados del cuadrilátero y las extensiones de sus diagonales). Por lo tanto, un cuadrilátero convexo es tangencial si y solo si los excentros en estos cuatro excírculos son los vértices de un cuadrilátero cíclico . ^{[1] : p. 73}

Un cuadrilátero convexo ABCD , con diagonales que se cortan en P , es tangencial si y solo si los cuatro excentros en los triángulos APB , BPC , CPD y DPA opuestos a los vértices B y D son concíclicos. ^{[1] : p. 79} Si R _a , R _b , R _c y R _d son los exradios en los triángulos APB , BPC , CPD y DPA opuestos respectivamente a los vértices B y D , entonces otra condición es que el cuadrilátero es tangencial si y solo si ^{[1] : p. 80}

${\displaystyle {\frac {1}{R_{a}}}+{\frac {1}{R_{c}}}={\frac {1}{R_{b}}}+{\frac {1}{R_{d}}}.}$

Además, un cuadrilátero convexo ABCD con diagonales que se intersecan en P es tangencial si y solo si ^[5]

${\displaystyle {\frac {a}{\triangle (APB)}}+{\frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}}$

donde ∆( APB ) es el área del triángulo APB .

Denotemos los segmentos en los que la intersección diagonal P divide la diagonal AC como AP = p ₁ y PC = p ₂ , y de manera similar P divide la diagonal BD en los segmentos BP = q ₁ y PD = q ₂ . Entonces el cuadrilátero es tangencial si y solo si cualquiera de las siguientes igualdades es verdadera: ^[30]

${\displaystyle ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}}$

o ^{[1] : pág. 74}

${\displaystyle {\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}}$

o ^{[1] : pág. 77}

${\displaystyle {\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.}$

Condiciones para que un cuadrilátero tangencial sea otro tipo de cuadrilátero

Rombo

Un cuadrilátero tangencial es un rombo si y sólo si sus ángulos opuestos son iguales. ^[31]

Cometa

Un cuadrilátero tangencial es una cometa si y sólo si se cumple alguna de las siguientes condiciones: ^[17]

• El área es la mitad del producto de las diagonales .
• Las diagonales son perpendiculares .
• Los dos segmentos de línea que conectan puntos de tangencia opuestos tienen longitudes iguales.
• Un par de longitudes tangentes opuestas tienen longitudes iguales.
• Los bimedianos tienen longitudes iguales.
• Los productos de lados opuestos son iguales.
• El centro del círculo inscrito se encuentra en la diagonal que es el eje de simetría.

Cuadrilátero bicéntrico

Un cuadrilátero bicéntrico ABCD : el cuadrilátero de contacto (rosa) es ortodiagonal.

Si el incírculo es tangente a los lados AB , BC , CD , DA en W , X , Y , Z respectivamente, entonces un cuadrilátero tangencial ABCD también es cíclico (y por lo tanto bicéntrico ) si y solo si se cumple alguna de las siguientes condiciones: ^{[2] [3] : p.124  [20]}

• WY es perpendicular a XZ
• ${\displaystyle AW\cdot CY=BW\cdot DY}$
• ${\displaystyle {\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}}$

El primero de estos tres significa que el cuadrilátero de contacto WXYZ es un cuadrilátero ortodiagonal .

Un cuadrilátero tangencial es bicéntrico si y sólo si su radio interno es mayor que el de cualquier otro cuadrilátero tangencial que tenga la misma secuencia de longitudes de lados. ^{[32] : pp.392–393}

Trapecio tangencial

Si el círculo inscrito es tangente a los lados AB y CD en W e Y respectivamente, entonces un cuadrilátero tangencial ABCD también es un trapezoide con lados paralelos AB y CD si y solo si ^{[33] : Teo. 2}

${\displaystyle AW\cdot DY=BW\cdot CY}$

y AD y BC son los lados paralelos de un trapezoide si y solo si

${\displaystyle AW\cdot BW=CY\cdot DY.}$

Véase también

• Círculo circunscrito
• Cuadrilátero ex-tangencial
• Triángulo tangencial
• Polígono tangencial

Referencias

1. Josefsson, Martin (2011), "Más caracterizaciones de cuadriláteros tangenciales" (PDF) , Forum Geometricorum , 11 : 65–82.
2. Bryant, Victor; Duncan, John (2010), "Ruedas dentro de ruedas", The Mathematical Gazette , 94 (noviembre): 502–505.
3. Josefsson, Martin (2010), "Cálculos relativos a las longitudes de tangentes y cuerdas de tangencia de un cuadrilátero tangencial" (PDF) , Forum Geometricorum , 10 : 119–130.
4. Andreescu, Titu; Enescu, Bogdan (2006), Tesoros de la Olimpiada Matemática , Birkhäuser, págs. 64–68.
5. Minculete, Nicusor (2009), "Caracterizaciones de un cuadrilátero tangencial" (PDF) , Forum Geometricorum , 9 : 113–118.
6. Josefsson, Martin (2012), "Caracterizaciones métricas similares de cuadriláteros tangenciales y extangenciales" (PDF) , Forum Geometricorum , 12 : 63–77
7. Durell, CV; Robson, A. (2003), Trigonometría avanzada , reimpresión de Dover, págs. 28-30.
8. Hajja, Mowaffaq (2008), "Una condición para que un cuadrilátero circunscriptible sea cíclico" (PDF) , Forum Geometricorum , 8 : 103–106.
9. Siddons, AW; Hughes, RT (1929), Trigonometría , Cambridge Univ. Press, pág. 203.
10. Grinberg, Darij, Cuadriláteros circunscritos revisitados, 2008
11. Yiu, Paul, Geometría euclidiana , [1], 1998, págs. 156–157.
12. Hoyt, John P. (1986), "Maximización del área de un trapecio", American Mathematical Monthly , 93 (1): 54–56, doi :10.2307/2322549.
13. Publicado en El arte de resolver problemas, 2012
14. Hoyt, John P. (1984), "Quickies, Q694", Revista de Matemáticas , 57 (4): 239, 242.
15. Josefsson, Martin (2010), "Sobre el radio interno de un cuadrilátero tangencial" (PDF) , Forum Geometricorum , 10 : 27–34.
16. Bogomolny, Alexander (2016), Una relación de Inradii en un cuadrilátero inscriptible, Cut-the-knot , [2].
17. Josefsson, Martin (2011), "¿Cuándo un cuadrilátero tangencial es una cometa?" (PDF) , Forum Geometricorum , 11 : 165–174.
18. Josefsson, Martin (2011), "El área de un cuadrilátero bicéntrico" (PDF) , Forum Geometricorum , 11 : 155–164.
19. Gutierrez, Antonio, "Cuadrilátero circunscrito, diagonal, cuerda, proporción", [3], consultado 2012-04-09.
20. Josefsson, Martin (2010), "Caracterizaciones de cuadriláteros bicéntricos" (PDF) , Forum Geometricorum , 10 : 165–173.
21. Myakishev, Alexei (2006), "Sobre dos líneas notables relacionadas con un cuadrilátero" (PDF) , Forum Geometricorum , 6 : 289–295.
22. Dergiades, Nikolaos; Christodoulou, Dimitris M. (2017), "Los dos incentros de un cuadrilátero convexo arbitrario" (PDF) , Forum Geometricorum , 17 : 245–254.
23. Andreescu, Titu; Feng, Zuming (2005), 103 problemas de trigonometría del entrenamiento del equipo IMO de EE. UU. , Birkhäuser, págs. 176-177.
24. "Determinar la relación OM/ON", publicación en Art of Problem Solving, 2011
25. Barton, Helen (1926), "Sobre un círculo unido a una barra de cuatro barras plegable", American Mathematical Monthly , 33 (9): 462–465, doi :10.2307/2299611, JSTOR  2299611.
26. Bogomolny, Alexander, "¿Cuándo un cuadrilátero es inscriptible?", Miscelánea y rompecabezas matemáticos interactivos , [4].
27. Chao, Wu Wei; Simeonov, Plamen (2000), "Cuando los cuadriláteros tienen círculos inscritos (solución al problema 10698)", American Mathematical Monthly , 107 (7): 657–658, doi :10.2307/2589133.
28. Vaynshtejn, I.; Vasiliev, N.; Senderov, V. (1995), "(Solución al problema) M1495", Kvant (6): 27–28.
29. Josefsson, Martin (2012), "Caracterizaciones de cuadriláteros ortodiagonales" (PDF) , Forum Geometricorum , 12 : 13–25.
30. Hoehn, Larry (2011), "Una nueva fórmula sobre las diagonales y los lados de un cuadrilátero" (PDF) , Forum Geometricorum , 11 : 211–212.
31. De Villiers, Michael (2011), "Polígonos cíclicos equiangulares y polígonos circunscritos equiláteros", Mathematical Gazette , 95 (marzo): 102–107.
32. Hess, Albrecht (2014), "Sobre un círculo que contiene los incentros de cuadriláteros tangenciales" (PDF) , Forum Geometricorum , 14 : 389–396.
33. Josefsson, Martin (2014), "El triángulo de punta diagonal revisitado" (PDF) , Forum Geometricorum , 14 : 381–385.

Enlaces externos

• Weisstein, Eric W. , "Cuadrilátero tangencial", MathWorld