Relación entre el perímetro de la lemniscata de Bernoulli y su diámetro
Lemniscata de Bernoulli En matemáticas , la constante lemniscata ϖ es una constante matemática trascendental que es la relación entre el perímetro de la lemniscata de Bernoulli y su diámetro , análoga a la definición de π para el círculo. [1] De manera equivalente, el perímetro de la lemniscata es 2 ϖ funciones elípticas lemniscatas y es aproximadamente igual a 2,62205755. [2] También aparece en la evaluación de la función gamma y beta en ciertos valores racionales. El símbolo ϖ es una variante cursiva de π ; véase Pi § Variante pi . ( incógnita 2 + y 2 ) 2 = incógnita 2 − y 2 {\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
A veces las cantidades 2 ϖ o ϖ/2 lemniscata . [3] [4]
A partir de 2024 se habrán calculado más de 1,2 billones de dígitos de esta constante. [5]
Historia La constante de Gauss , denotada por G , es igual a ϖ / π ≈ 0,8346268 [6] y lleva el nombre de Carl Friedrich Gauss , quien la calculó a través de la media aritmético-geométrica como . En 1799, Gauss tenía dos pruebas del teorema de que donde es la constante lemniscata. [8] 1 / METRO ( 1 , 2 ) {\displaystyle 1/M{\bigl (}1,{\sqrt {2}}{\bigr )}} METRO ( 1 , 2 ) = π / ϖ {\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}=\pi /\varpi } ϖ {\estilo de visualización \varpi}
John Todd nombró dos constantes lemniscatas más, la primera constante lemniscata A = ϖ /2 ≈ 1,3110287771segunda constante lemniscata B = π /(2 ϖ ) ≈ 0,5990701173[9] [10] [11]
La constante lemniscata y la primera constante lemniscata de Todd fueron demostradas trascendentales por Carl Ludwig Siegel en 1932 y más tarde por Theodor Schneider en 1937 y la segunda constante lemniscata de Todd y la constante de Gauss fueron demostradas trascendentales por Theodor Schneider en 1941. [9] [12] [13] En 1975, Gregory Chudnovsky demostró que el conjunto es algebraicamente independiente sobre , lo que implica que y también son algebraicamente independientes. [14] [15] Pero el conjunto (donde el primo denota la derivada con respecto a la segunda variable) no es algebraicamente independiente sobre . [16] En 1996, Yuri Nesterenko demostró que el conjunto es algebraicamente independiente sobre . [17] ϖ {\estilo de visualización \varpi} A {\estilo de visualización A} B {\estilo de visualización B} GRAMO {\estilo de visualización G} { π , ϖ } {\displaystyle \{\pi ,\varpi \}} Q {\displaystyle \mathbb {Q}} A {\estilo de visualización A} B {\estilo de visualización B} { π , METRO ( 1 , 1 / 2 ) , METRO " ( 1 , 1 / 2 ) } {\displaystyle {\bigl \{}\pi ,M{\bigl (}1,1/{\sqrt {2}}{\bigr )},M'{\bigl (}1,1/{\sqrt {2}}{\bigr )}{\bigr \}}} Q {\displaystyle \mathbb {Q}} { π , ϖ , mi π } {\displaystyle \{\pi ,\varpi ,e^{\pi }\}} Q {\displaystyle \mathbb {Q}}
Formularios Generalmente se define por la primera igualdad a continuación, pero tiene muchas formas equivalentes: [18] ϖ {\estilo de visualización \varpi}
ϖ = 2 ∫ 0 1 d a 1 − a 4 = 2 ∫ 0 ∞ d a 1 + a 4 = ∫ 0 1 d a a − a 3 = ∫ 1 ∞ d a a 3 − a = 4 ∫ 0 ∞ ( 1 + a 4 4 − a ) d a = 2 2 ∫ 0 1 1 − a 4 4 d a = 3 ∫ 0 1 1 − a 4 d a = 2 K ( i ) = 1 2 B ( 1 4 , 1 2 ) = 1 2 2 B ( 1 4 , 1 4 ) = Γ ( 1 / 4 ) 2 2 2 π = 2 − 2 4 o ( 3 / 4 ) 2 o ( 1 / 4 ) 2 = 2.62205 75542 92119 81046 48395 89891 11941 … , {\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}= {\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0} ^{1}{\frac {\mathrm {d} t}{\sqrt {tt^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t} {\sqrt {t^{3}-t}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t ^{4}}}-t{\Más grande )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\matop { \mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&=2K(i )={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={ \tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3 /4)^{2}}{\zeta (1/4)^{2}}}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{alineado}}}
donde K es la integral elíptica completa de primer tipo con módulo k , Β es la función beta , Γ es la función gamma y ζ es la función zeta de Riemann .
La constante lemniscata también se puede calcular mediante la media aritmético-geométrica , METRO {\estilo de visualización M}
ϖ = π METRO ( 1 , 2 ) . {\displaystyle \varpi ={\frac {\pi }{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}.}
La constante de Gauss se define típicamente como el recíproco de la media aritmético-geométrica de 1 y la raíz cuadrada de 2 , según su cálculo publicado en 1800: Las constantes lemniscatas de John Todd se pueden dar en términos de la función beta B: METRO ( 1 , 2 ) {\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}} GRAMO = 1 METRO ( 1 , 2 ) {\displaystyle G={\frac {1}{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}} A = ϖ 2 = 1 4 B ( 1 4 , 1 2 ) , B = π 2 ϖ = 1 4 B ( 1 2 , 3 4 ) . {\displaystyle {\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{ 4}},{\tfrac {1}{2}}{\bigr )},\\[3mu]B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4} }\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}
Como valor especial de las funciones L β " ( 0 ) = registro ϖ π {\displaystyle \beta '(0)=\log {\frac {\varpi }{\sqrt {\pi }}}}
que es análogo a
o " ( 0 ) = registro 1 2 π {\displaystyle \zeta '(0)=\log {\frac {1}{\sqrt {2\pi }}}}
donde es la función beta de Dirichlet y es la función zeta de Riemann . [20] β {\displaystyle \beta } ζ {\displaystyle \zeta }
Análogamente a la fórmula de Leibniz para π ,
tenemos [21] [22] [23] [24] [25]
donde es la función L de la curva elíptica sobre ; esto significa que es la función multiplicativa dada por
donde es el número de soluciones de la congruencia
en variables que son números enteros no negativos ( es el conjunto de todos los primos). Equivalentemente, viene dada por
donde tales que y es la función eta . [26] [27] [28]
El resultado anterior se puede escribir de forma equivalente como
(el número es el conductor de ) y también nos dice que la conjetura BSD es verdadera para el anterior . [29]
Los primeros valores de vienen dados por la siguiente tabla; si tal que no aparece en la tabla, entonces : β ( 1 ) = ∑ n = 1 ∞ χ ( n ) n = π 4 , {\displaystyle \beta (1)=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n}}={\frac {\pi }{4}},} L ( E , 1 ) = ∑ n = 1 ∞ ν ( n ) n = ϖ 4 {\displaystyle L(E,1)=\sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}={\frac {\varpi }{4}}} L {\displaystyle L} E : y 2 = x 3 − x {\displaystyle E:\,y^{2}=x^{3}-x} Q {\displaystyle \mathbb {Q} } ν {\displaystyle \nu } ν ( p n ) = { p − N p , p ∈ P , n = 1 0 , p = 2 , n ≥ 2 ν ( p ) ν ( p n − 1 ) − p ν ( p n − 2 ) , p ∈ P ∖ { 2 } , n ≥ 2 {\displaystyle \nu (p^{n})={\begin{cases}p-{\mathcal {N}}_{p},&p\in \mathbb {P} ,\,n=1\\[5mu]0,&p=2,\,n\geq 2\\[5mu]\nu (p)\nu (p^{n-1})-p\nu (p^{n-2}),&p\in \mathbb {P} \setminus \{2\},\,n\geq 2\end{cases}}} N p {\displaystyle {\mathcal {N}}_{p}} a 3 − a ≡ b 2 ( mod p ) , p ∈ P {\displaystyle a^{3}-a\equiv b^{2}\,(\operatorname {mod} p),\quad p\in \mathbb {P} } a , b {\displaystyle a,b} P {\displaystyle \mathbb {P} } ν {\displaystyle \nu } F ( τ ) = η ( 4 τ ) 2 η ( 8 τ ) 2 = ∑ n = 1 ∞ ν ( n ) q n , q = e 2 π i τ {\displaystyle F(\tau )=\eta (4\tau )^{2}\eta (8\tau )^{2}=\sum _{n=1}^{\infty }\nu (n)q^{n},\quad q=e^{2\pi i\tau }} τ ∈ C {\displaystyle \tau \in \mathbb {C} } ℑ τ > 0 {\displaystyle \operatorname {\Im } \tau >0} η {\displaystyle \eta } ∑ n = 1 ∞ ν ( n ) n e − 2 π n / 32 = ϖ 8 {\displaystyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}e^{-2\pi n/{\sqrt {32}}}={\frac {\varpi }{8}}} 32 {\displaystyle 32} E {\displaystyle E} E {\displaystyle E} ν {\displaystyle \nu } 1 ≤ n ≤ 113 {\displaystyle 1\leq n\leq 113} n {\displaystyle n} ν ( n ) = 0 {\displaystyle \nu (n)=0} n ν ( n ) n ν ( n ) 1 1 53 14 5 − 2 61 − 10 9 − 3 65 − 12 13 6 73 − 6 17 2 81 9 25 − 1 85 − 4 29 − 10 89 10 37 − 2 97 18 41 10 101 − 2 45 6 109 6 49 − 7 113 − 14 {\displaystyle {\begin{array}{|c|c|c|c|}\hline n&\nu (n)&n&\nu (n)\\\hline 1&1&53&14\\\hline 5&-2&61&-10\\\hline 9&-3&65&-12\\\hline 13&6&73&-6\\\hline 17&2&81&9\\\hline 25&-1&85&-4\\\hline 29&-10&89&10\\\hline 37&-2&97&18\\\hline 41&10&101&-2\\\hline 45&6&109&6\\\hline 49&-7&113&-14\\\hline \end{array}}}
Como valor especial de otras funciones Sea el nivel de peso mínimo de la nueva forma. Entonces [30]
El coeficiente de es la función tau de Ramanujan . Δ {\displaystyle \Delta } 1 {\displaystyle 1} Δ ( i ) = 1 64 ( ϖ π ) 12 . {\displaystyle \Delta (i)={\frac {1}{64}}\left({\frac {\varpi }{\pi }}\right)^{12}.} q {\displaystyle q} Δ {\displaystyle \Delta }
Serie La fórmula de Viète para π se puede escribir:
2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1 2 1 2 ⋯ {\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
Una fórmula análoga para ϖ es: [31]
2 ϖ = 1 2 ⋅ 1 2 + 1 2 / 1 2 ⋅ 1 2 + 1 2 / 1 2 + 1 2 / 1 2 ⋯ {\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
El producto de Wallis para π es:
π 2 = ∏ n = 1 ∞ ( 1 + 1 n ) ( − 1 ) n + 1 = ∏ n = 1 ∞ ( 2 n 2 n − 1 ⋅ 2 n 2 n + 1 ) = ( 2 1 ⋅ 2 3 ) ( 4 3 ⋅ 4 5 ) ( 6 5 ⋅ 6 7 ) ⋯ {\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }
Una fórmula análoga para ϖ es: [32]
ϖ 2 = ∏ n = 1 ∞ ( 1 + 1 2 n ) ( − 1 ) n + 1 = ∏ n = 1 ∞ ( 4 n − 1 4 n − 2 ⋅ 4 n 4 n + 1 ) = ( 3 2 ⋅ 4 5 ) ( 7 6 ⋅ 8 9 ) ( 11 10 ⋅ 12 13 ) ⋯ {\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }
Un resultado relacionado para la constante de Gauss ( ) es: [33] G = ϖ / π {\displaystyle G=\varpi /\pi }
ϖ π = ∏ n = 1 ∞ ( 4 n − 1 4 n ⋅ 4 n + 2 4 n + 1 ) = ( 3 4 ⋅ 6 5 ) ( 7 8 ⋅ 10 9 ) ( 11 12 ⋅ 14 13 ) ⋯ {\displaystyle {\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }
Una serie infinita descubierta por Gauss es: [34]
ϖ π = ∑ n = 0 ∞ ( − 1 ) n ∏ k = 1 n ( 2 k − 1 ) 2 ( 2 k ) 2 = 1 − 1 2 2 2 + 1 2 ⋅ 3 2 2 2 ⋅ 4 2 − 1 2 ⋅ 3 2 ⋅ 5 2 2 2 ⋅ 4 2 ⋅ 6 2 + ⋯ {\displaystyle {\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }
La fórmula de Machin para π es y se pueden desarrollar varias fórmulas similares para π utilizando identidades trigonométricas de suma de ángulos, por ejemplo, la fórmula de Euler . Se pueden desarrollar fórmulas análogas para ϖ , incluidas las siguientes encontradas por Gauss: , donde es el arcoseno de la lemniscata . [35] 1 4 π = 4 arctan 1 5 − arctan 1 239 , {\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},} 1 4 π = arctan 1 2 + arctan 1 3 {\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}} 1 2 ϖ = 2 arcsl 1 2 + arcsl 7 23 {\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}} arcsl {\displaystyle \operatorname {arcsl} }
La constante lemniscata se puede calcular rápidamente mediante la serie [36] [37]
ϖ = 2 − 1 / 2 π ( ∑ n ∈ Z e − π n 2 ) 2 = 2 1 / 4 π e − π / 12 ( ∑ n ∈ Z ( − 1 ) n e − π p n ) 2 {\displaystyle \varpi =2^{-1/2}\pi {\biggl (}\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}{\biggr )}^{2}=2^{1/4}\pi e^{-\pi /12}{\biggl (}\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}{\biggr )}^{2}} donde (estos son los números pentagonales generalizados ). También [38] p n = 1 2 ( 3 n 2 − n ) {\displaystyle p_{n}={\tfrac {1}{2}}(3n^{2}-n)}
∑ m , n ∈ Z e − 2 π ( m 2 + m n + n 2 ) = 1 + 3 ϖ 12 1 / 8 π . {\displaystyle \sum _{m,n\in \mathbb {Z} }e^{-2\pi (m^{2}+mn+n^{2})}={\sqrt {1+{\sqrt {3}}}}{\dfrac {\varpi }{12^{1/8}\pi }}.} En un espíritu similar al del problema de Basilea ,
∑ z ∈ Z [ i ] ∖ { 0 } 1 z 4 = G 4 ( i ) = ϖ 4 15 {\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}} donde son los números enteros gaussianos y es la serie de Eisenstein de pesos ( ver Funciones elípticas lemniscatas § Números de Hurwitz para un resultado más general). [39] Z [ i ] {\displaystyle \mathbb {Z} [i]} G 4 {\displaystyle G_{4}} 4 {\displaystyle 4}
Un resultado relacionado es
∑ n = 1 ∞ σ 3 ( n ) e − 2 π n = ϖ 4 80 π 4 − 1 240 {\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}} donde es la suma de los divisores positivos de la función . [40] σ 3 {\displaystyle \sigma _{3}}
En 1842, Malmsten encontró
β ′ ( 1 ) = ∑ n = 1 ∞ ( − 1 ) n + 1 log ( 2 n + 1 ) 2 n + 1 = π 4 ( γ + 2 log π ϖ 2 ) {\displaystyle \beta '(1)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)} donde es la constante de Euler y es la función Dirichlet-Beta. γ {\displaystyle \gamma } β ( s ) {\displaystyle \beta (s)}
La constante de lemniscata viene dada por la serie rápidamente convergente
ϖ = π 32 4 e − π 3 ( ∑ n = − ∞ ∞ ( − 1 ) n e − 2 n π ( 3 n + 1 ) ) 2 . {\displaystyle \varpi =\pi {\sqrt[{4}]{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.}
La constante también viene dada por el producto infinito
ϖ = π ∏ m = 1 ∞ tanh 2 ( π m 2 ) . {\displaystyle \varpi =\pi \prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).} También [41]
∑ n = 0 ∞ ( − 1 ) n 6635520 n ( 4 n ) ! n ! 4 = 24 5 7 / 4 ϖ 2 π 2 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{6635520^{n}}}{\frac {(4n)!}{n!^{4}}}={\frac {24}{5^{7/4}}}{\frac {\varpi ^{2}}{\pi ^{2}}}.}
Fracciones continuas Una fracción continua (generalizada) para π es
Una fórmula análoga para ϖ es [10] π 2 = 1 + 1 1 + 1 ⋅ 2 1 + 2 ⋅ 3 1 + 3 ⋅ 4 1 + ⋱ {\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}} ϖ 2 = 1 + 1 2 + 2 ⋅ 3 2 + 4 ⋅ 5 2 + 6 ⋅ 7 2 + ⋱ {\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}
Defina la fracción continua de Brouncker [42]
Sea excepto por la primera igualdad donde . Entonces [43] [44]
Por ejemplo, b ( s ) = s + 1 2 2 s + 3 2 2 s + 5 2 2 s + ⋱ , s > 0. {\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.} n ≥ 0 {\displaystyle n\geq 0} n ≥ 1 {\displaystyle n\geq 1} b ( 4 n ) = ( 4 n + 1 ) ∏ k = 1 n ( 4 k − 1 ) 2 ( 4 k − 3 ) ( 4 k + 1 ) π ϖ 2 b ( 4 n + 1 ) = ( 2 n + 1 ) ∏ k = 1 n ( 2 k ) 2 ( 2 k − 1 ) ( 2 k + 1 ) 4 π b ( 4 n + 2 ) = ( 4 n + 1 ) ∏ k = 1 n ( 4 k − 3 ) ( 4 k + 1 ) ( 4 k − 1 ) 2 ϖ 2 π b ( 4 n + 3 ) = ( 2 n + 1 ) ∏ k = 1 n ( 2 k − 1 ) ( 2 k + 1 ) ( 2 k ) 2 π . {\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}} b ( 1 ) = 4 π , b ( 2 ) = ϖ 2 π , b ( 3 ) = π , b ( 4 ) = 9 π ϖ 2 . {\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }},&b(2)&={\frac {\varpi ^{2}}{\pi }},&b(3)&=\pi ,&b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}
De hecho, los valores de y , acoplados con la ecuación funcional,
determinan los valores de para todo . b ( 1 ) {\displaystyle b(1)} b ( 2 ) {\displaystyle b(2)} b ( s + 2 ) = ( s + 1 ) 2 b ( s ) , {\displaystyle b(s+2)={\frac {(s+1)^{2}}{b(s)}},} b ( n ) {\displaystyle b(n)} n {\displaystyle n}
Fracciones continuas simples Las fracciones continuas simples para la constante lemniscata y constantes relacionadas incluyen [45] [46] ϖ = [ 2 , 1 , 1 , 1 , 1 , 1 , 4 , 1 , 2 , … ] , 2 ϖ = [ 5 , 4 , 10 , 2 , 1 , 2 , 3 , 29 , … ] , ϖ 2 = [ 1 , 3 , 4 , 1 , 1 , 1 , 5 , 2 , … ] , ϖ π = [ 0 , 1 , 5 , 21 , 3 , 4 , 14 , … ] . {\displaystyle {\begin{aligned}\varpi &=[2,1,1,1,1,1,4,1,2,\ldots ],\\[8mu]2\varpi &=[5,4,10,2,1,2,3,29,\ldots ],\\[5mu]{\frac {\varpi }{2}}&=[1,3,4,1,1,1,5,2,\ldots ],\\[2mu]{\frac {\varpi }{\pi }}&=[0,1,5,21,3,4,14,\ldots ].\end{aligned}}}
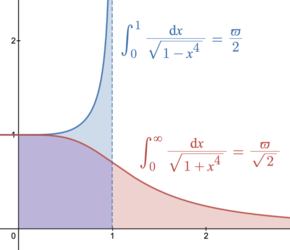
Integrales Una representación geométrica de y ϖ / 2 {\displaystyle \varpi /2} ϖ / 2 {\displaystyle \varpi /{\sqrt {2}}} La constante lemniscata ϖ está relacionada con el área bajo la curva . Definiendo , el doble del área en el cuadrante positivo bajo la curva es En el caso cuártico, x 4 + y 4 = 1 {\displaystyle x^{4}+y^{4}=1} π n := B ( 1 n , 1 n ) {\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}} x n + y n = 1 {\displaystyle x^{n}+y^{n}=1} 2 ∫ 0 1 1 − x n n d x = 1 n π n . {\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.} 1 4 π 4 = 1 2 ϖ . {\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}
En 1842, Malmsten descubrió que [47]
∫ 0 1 log ( − log x ) 1 + x 2 d x = π 2 log π ϖ 2 . {\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}
Además, ∫ 0 ∞ tanh x x e − x d x = log ϖ 2 π {\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}
y [48]
∫ 0 ∞ e − x 4 d x = 2 ϖ 2 π 4 , analogous to ∫ 0 ∞ e − x 2 d x = π 2 , {\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},} integral gaussiana .
La constante lemniscata aparece en la evaluación de las integrales
π ϖ = ∫ 0 π 2 sin ( x ) d x = ∫ 0 π 2 cos ( x ) d x {\displaystyle {\frac {\pi }{\varpi }}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}
ϖ π = ∫ 0 ∞ d x cosh ( π x ) {\displaystyle {\frac {\varpi }{\pi }}=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}
Las constantes lemniscatas de John Todd se definen mediante integrales: [9]
A = ∫ 0 1 d x 1 − x 4 {\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}
B = ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Circunferencia de una elipse La constante lemniscata satisface la ecuación
π ϖ = 2 ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle {\frac {\pi }{\varpi }}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Euler descubrió en 1738 que para la elástica rectangular (constantes de primera y segunda lemniscata) [50]
arc length ⋅ height = A ⋅ B = ∫ 0 1 d x 1 − x 4 ⋅ ∫ 0 1 x 2 d x 1 − x 4 = ϖ 2 ⋅ π 2 ϖ = π 4 {\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}
Ahora, considerando la circunferencia de la elipse con ejes y , satisfaciendo , Stirling notó que C {\displaystyle C} 2 {\displaystyle {\sqrt {2}}} 1 {\displaystyle 1} 2 x 2 + 4 y 2 = 1 {\displaystyle 2x^{2}+4y^{2}=1}
C 2 = ∫ 0 1 d x 1 − x 4 + ∫ 0 1 x 2 d x 1 − x 4 {\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Por lo tanto la circunferencia completa es
C = π ϖ + ϖ = 3.820197789 … {\displaystyle C={\frac {\pi }{\varpi }}+\varpi =3.820197789\ldots }
Esta es también la longitud del arco de la curva sinusoidal en medio período: [52]
C = ∫ 0 π 1 + cos 2 ( x ) d x {\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}
Otros límites De manera análoga a
donde están los números de Bernoulli , tenemos
donde están los números de Hurwitz . 2 π = lim n → ∞ | ( 2 n ) ! B 2 n | 1 2 n {\displaystyle 2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}} B n {\displaystyle \mathrm {B} _{n}} 2 ϖ = lim n → ∞ ( ( 4 n ) ! H 4 n ) 1 4 n {\displaystyle 2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}} H n {\displaystyle \mathrm {H} _{n}}
Notas ^ Ver:Gauss, CF (1866). Werke (Banda III) (en latín y alemán). Herausgegeben der Königlichen Gesellschaft der Wissenschaften zu Göttingen. Cox 1984, pág. 281 Eymard, Pierre; Lafon, Jean-Pierre (2004). El número Pi . Sociedad Matemática Estadounidense. ISBN 0-8218-3246-8 Bottazzini, Umberto ; Gray, Jeremy (2013). Armonía oculta: fantasías geométricas: el auge de la teoría de funciones complejas . Springer. doi :10.1007/978-1-4614-5725-1. ISBN . 978-1-4614-5724-4 Arakawa, Tsuneo; Ibukiyama, Tomoyoshi; Kaneko, Masanobu (2014). Números de Bernoulli y funciones Zeta . Saltador. ISBN 978-4-431-54918-5 ^ Ver:Finch 2003, pág. 420 Kobayashi, Hiroyuki; Takeuchi, Shingo (2019), "Aplicaciones de funciones trigonométricas generalizadas con dos parámetros", Communications on Pure & Applied Analysis , 18 (3): 1509–1521, arXiv : 1903.07407 , doi :10.3934/cpaa.2019072, S2CID 102487670 Asai, Tetsuya (2007), Sumas de Gauss elípticas y valores L de Hecke en s=1 , arXiv : 0707.3711 "A062539 - Oís". ^ "A064853 - Oís". ^ "Constante de lemniscata". ^ "Récords establecidos por y-cruncher". numberworld.org . Consultado el 20 de agosto de 2024 . ^ "A014549 - Oís". ^ Ninguna de estas pruebas era rigurosa desde el punto de vista moderno. Véase Cox 1984, p. 281. ^ abc Todd, John (enero de 1975). "Las constantes lemniscatas". Comunicaciones de la ACM . 18 (1): 14–19. doi : 10.1145/360569.360580 . S2CID 85873. ^ desde "A085565 - Oeis". "A076390 - Oeis". ^ Carlson, BC (2010), "Integrales elípticas", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual del NIST de funciones matemáticas , Cambridge University Press, ISBN 978-0-521-19225-5 ^ En particular, Siegel demostró que si y con son algebraicas, entonces o es trascendental. Aquí, y son series de Eisenstein . El hecho de que es trascendental se sigue de y G 4 ( ω 1 , ω 2 ) {\displaystyle \operatorname {G} _{4}(\omega _{1},\omega _{2})} G 6 ( ω 1 , ω 2 ) {\displaystyle \operatorname {G} _{6}(\omega _{1},\omega _{2})} Im ( ω 2 / ω 1 ) > 0 {\displaystyle \operatorname {Im} (\omega _{2}/\omega _{1})>0} ω 1 {\displaystyle \omega _{1}} ω 2 {\displaystyle \omega _{2}} G 4 {\displaystyle \operatorname {G} _{4}} G 6 {\displaystyle \operatorname {G} _{6}} ϖ {\displaystyle \varpi } G 4 ( ϖ , ϖ i ) = 1 / 15 {\displaystyle \operatorname {G} _{4}(\varpi ,\varpi i)=1/15} G 6 ( ϖ , ϖ i ) = 0. {\displaystyle \operatorname {G} _{6}(\varpi ,\varpi i)=0.}
Apostol, TM (1990). Funciones modulares y series de Dirichlet en la teoría de números (segunda edición). Springer. pág. 12. ISBN 0-387-97127-0
Siegel, CL (1932). "Über die Perioden elliptischer Funktionen". Journal für die reine und angewandte Mathematik 167 : 62–69. ^ En particular, Schneider demostró que la función beta es trascendental para todos los tales que . El hecho de que es trascendental se sigue de y de manera similar para B y G de B ( a , b ) {\displaystyle \mathrm {B} (a,b)} a , b ∈ Q ∖ Z {\displaystyle a,b\in \mathbb {Q} \setminus \mathbb {Z} } a + b ∉ Z 0 − {\displaystyle a+b\notin \mathbb {Z} _{0}^{-}} ϖ {\displaystyle \varpi } ϖ = 1 2 B ( 1 4 , 1 2 ) {\displaystyle \varpi ={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}} B ( 1 2 , 3 4 ) . {\displaystyle \mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.}
Schneider, Theodor (1941). "Zur Theorie der Abelschen Funktionen und Integrale". Journal für die reine und angewandte Mathematik . 183 (19): 110-128. doi :10.1515/crll.1941.183.110. S2CID 118624331. ^ GV Choodnovsky: Independencia algebraica de las constantes relacionadas con las funciones de análisis , Avisos de la AMS 22, 1975, pág. A-486 ^ GV Chudnovsky: Contribuciones a la teoría de los números trascendentales , American Mathematical Society, 1984, pág. 6 ^ De hecho, π = 2 2 M 3 ( 1 , 1 2 ) M ′ ( 1 , 1 2 ) = 1 G 3 M ′ ( 1 , 1 2 ) . {\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.}
Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi y el AGM: un estudio sobre teoría analítica de números y complejidad computacional (Primera edición). Wiley-Interscience. ISBN 0-471-83138-7 ^ Nesterenko, YV; Philippon, P. (2001). Introducción a la teoría de la independencia algebraica . Springer. pág. 27. ISBN 3-540-41496-7 ^ Ver:Cox 1984, pág. 281 Finch 2003, págs. 420–422 Schappacher, Norbert (1997). "Algunos hitos de la lemniscatomía" (PDF) . En Sertöz, S. (ed.). Geometría algebraica (Actas de la Escuela de verano de Bilkent, 7-19 de agosto de 1995, Ankara, Turquía). Marcel Dekker. pp. 257-290. ^ "A113847 - Oís". ^ Cremona, JE (1997). Algoritmos para curvas elípticas modulares (2.ª ed.). Cambridge University Press . ISBN 0521598206 ^ De hecho, la serie converge para . ∑ n = 1 ∞ ν ( n ) n s {\textstyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n^{s}}}} ℜ s > 5 / 6 {\displaystyle \operatorname {\Re } s>5/6} ^ Murty, Vijaya Kumar (1995). Seminario sobre el último teorema de Fermat . American Mathematical Society . pág. 16. ISBN. 9780821803134 ^ Cohen, Henri (1993). Un curso de teoría algebraica computacional de números . Springer-Verlag. pág. 382–406. ISBN 978-3-642-08142-2 ^ "Curva elíptica con etiqueta LMFDB 32.a3 (etiqueta Cremona 32a2)". Base de datos de funciones L y formas modulares . ^ La función es la nueva forma del nivel de peso único y satisface la ecuación funcional F {\displaystyle F} 2 {\displaystyle 2} 32 {\displaystyle 32} F ( − 1 τ ) = − τ 2 32 F ( τ 1 32 ) . {\displaystyle F\left(-{\frac {1}{\tau }}\right)=-{\frac {\tau ^{2}}{32}}F\left({\frac {\tau {\vphantom {1}}}{32}}\right).} ^ La función está estrechamente relacionada con la función que es la función multiplicativa definida por ν {\displaystyle \nu } ξ {\displaystyle \xi } ξ ( p n ) = { N p ′ , p ∈ P , n = 1 ξ ( p n − 1 ) + χ ( p ) n , p ∈ P , n ≥ 2 {\displaystyle \xi (p^{n})={\begin{cases}{\mathcal {N}}_{p}',&p\in \mathbb {P} ,\,n=1\\[5mu]\xi (p^{n-1})+\chi (p)^{n},&p\in \mathbb {P} ,\,n\geq 2\end{cases}}} N p ′ {\displaystyle {\mathcal {N}}_{p}'} a 2 + b 2 = p , p ∈ P {\displaystyle a^{2}+b^{2}=p,\quad p\in \mathbb {P} } el teorema de Fermat sobre las sumas de dos cuadrados ) y es el carácter de Dirichlet de la fórmula de Leibniz para π; también a , b {\displaystyle a,b} χ {\displaystyle \chi } ∑ d | n χ ( d ) = ξ ( n ) {\displaystyle \sum _{d|n}\chi (d)=\xi (n)} n {\displaystyle n} ν {\displaystyle \nu } ξ {\displaystyle \xi } ∑ k = 0 n ( − 1 ) k ξ ( 4 k + 1 ) ξ ( 4 n − 4 k + 1 ) = ν ( 2 n + 1 ) {\displaystyle \sum _{k=0}^{n}(-1)^{k}\xi (4k+1)\xi (4n-4k+1)=\nu (2n+1)} n {\displaystyle n} ^ La función también aparece en ν {\displaystyle \nu } ∑ z ∈ G ; z z ¯ = n z = ν ( n ) {\displaystyle \sum _{z\in \mathbb {G} ;\,z{\overline {z}}=n}z=\nu (n)} los enteros gaussianos de la forma n {\displaystyle n} G {\displaystyle \operatorname {\mathbb {G} } } ( − 1 ) a ± b − 1 2 ( a ± b i ) {\displaystyle (-1)^{\frac {a\pm b-1}{2}}(a\pm bi)} a {\displaystyle a} b {\displaystyle b} ξ {\displaystyle \xi } | { z : z ∈ G ∧ z z ¯ = n } | = ξ ( n ) {\displaystyle \left|\{z:z\in \mathbb {G} \land z{\overline {z}}=n\}\right|=\xi (n)} n {\displaystyle n} ^ Rubin, Karl (1987). "Grupos de Tate-Shafarevich y funciones L de curvas elípticas con multiplicación compleja". Inventiones mathematicae . 89 : 528. ^ "Newform orbit 1.12.aa". Base de datos de funciones L y formas modulares . ^ Levin (2006) ^ Hyde (2014) demuestra la validez de una fórmula más general tipo Wallis para las curvas de trébol; aquí el caso especial de la lemniscata se transforma ligeramente para mayor claridad. ^ Hyde, Trevor (2014). "Un producto de Wallis sobre tréboles" (PDF) . The American Mathematical Monthly . 121 (3): 237–243. doi :10.4169/amer.math.monthly.121.03.237. S2CID 34819500. ^ Bottazzini, Umberto ; Gray, Jeremy (2013). Armonía oculta: fantasías geométricas: el auge de la teoría de funciones complejas . Springer. doi :10.1007/978-1-4614-5725-1. ISBN . 978-1-4614-5724-4 ^ Todd (1975) ^ Cox 1984, p. 307, ecuación 2.21 para la primera igualdad. La segunda igualdad se puede demostrar utilizando el teorema del número pentagonal . ^ Berndt, Bruce C. (1998). Cuadernos de Ramanujan, parte V. Springer. ISBN 978-1-4612-7221-2 ^ Esta fórmula se puede demostrar por inversión hipergeométrica : Sea a ( q ) = ∑ m , n ∈ Z q m 2 + m n + n 2 {\displaystyle \operatorname {a} (q)=\sum _{m,n\in \mathbb {Z} }q^{m^{2}+mn+n^{2}}} q ∈ C {\displaystyle q\in \mathbb {C} } | q | < 1 {\displaystyle \left|q\right|<1} a ( q ) = 2 F 1 ( 1 3 , 2 3 , 1 , z ) {\displaystyle \operatorname {a} (q)={}_{2}F_{1}\left({\frac {1}{3}},{\frac {2}{3}},1,z\right)} q = exp ( − 2 π 3 2 F 1 ( 1 / 3 , 2 / 3 , 1 , 1 − z ) 2 F 1 ( 1 / 3 , 2 / 3 , 1 , z ) ) {\displaystyle q=\exp \left(-{\frac {2\pi }{\sqrt {3}}}{\frac {{}_{2}F_{1}(1/3,2/3,1,1-z)}{{}_{2}F_{1}(1/3,2/3,1,z)}}\right)} z ∈ C ∖ { 0 , 1 } {\displaystyle z\in \mathbb {C} \setminus \{0,1\}} z = 1 4 ( 3 3 − 5 ) {\textstyle z={\tfrac {1}{4}}{\bigl (}3{\sqrt {3}}-5{\bigr )}} ^ Eymard, Pedro; Lafon, Jean-Pierre (2004). El número Pi . Sociedad Matemática Estadounidense. ISBN 0-8218-3246-8 ^ Garrett, Paul. "Formas modulares elípticas de nivel uno" (PDF) . Universidad de Minnesota . ^ La fórmula se deduce de la transformación hipergeométrica 3 F 2 ( 1 4 , 1 2 , 3 4 , 1 , 1 , 16 z ( 1 − z ) 2 ( 1 + z ) 4 ) = ( 1 + z ) 2 F 1 ( 1 2 , 1 2 , 1 , z ) 2 {\displaystyle {}_{3}F_{2}\left({\frac {1}{4}},{\frac {1}{2}},{\frac {3}{4}},1,1,16z{\frac {(1-z)^{2}}{(1+z)^{4}}}\right)=(1+z)\,{}_{2}F_{1}\left({\frac {1}{2}},{\frac {1}{2}},1,z\right)^{2}} función lambda modular . z = λ ( 1 + 5 i ) {\displaystyle z=\lambda (1+5i)} λ {\displaystyle \lambda } ^ Khrushchev, Sergey (2008). Polinomios ortogonales y fracciones continuas (Primera edición). Cambridge University Press. ISBN 978-0-521-85419-1 4 [ Γ ( 3 + s / 4 ) / Γ ( 1 + s / 4 ) ] 2 {\displaystyle 4[\Gamma (3+s/4)/\Gamma (1+s/4)]^{2}} 4 [ Γ ( ( 3 + s ) / 4 ) / Γ ( ( 1 + s ) / 4 ) ] 2 {\displaystyle 4[\Gamma ((3+s)/4)/\Gamma ((1+s)/4)]^{2}} ^ Khrushchev, Sergey (2008). Polinomios ortogonales y fracciones continuas (Primera edición). Cambridge University Press. ISBN 978-0-521-85419-1 ^ Perron, Oskar (1957). Die Lehre von den Kettenbrüchen: Band II (en alemán) (Tercera ed.). BG Teubner. ^ "A062540 - OEIS". oeis.org . Consultado el 14 de septiembre de 2022 . ^ "A053002 - OEIS". oeis.org . ^ Blagouchine, Iaroslav V. (2014). "Redescubrimiento de las integrales de Malmsten, su evaluación mediante métodos de integración de contornos y algunos resultados relacionados". The Ramanujan Journal . 35 (1): 21–110. doi :10.1007/s11139-013-9528-5. S2CID 120943474. ^ "A068467 - Oís". ^ Levien (2008) ^ Adlaj, Semjon (2012). "Una fórmula elocuente para el perímetro de una elipse" (PDF) . American Mathematical Society . pág. 1097. También se podría observar que la longitud de la curva "seno" durante medio período, es decir, la longitud del gráfico de la función sin(t) desde el punto donde t = 0 hasta el punto donde t = π, es . 2 l ( 1 / 2 ) = L + M {\displaystyle {\sqrt {2}}l(1/{\sqrt {2}})=L+M} M = 1 / G = π / ϖ {\displaystyle M=1/G=\pi /\varpi } L = π / M = G π = ϖ {\displaystyle L=\pi /M=G\pi =\varpi }
Referencias Weisstein, Eric W. "Constante de lemniscata". MundoMatemático Secuencias A014549, A053002 y A062539 en OEIS Cox, David A. (enero de 1984). «La media aritmético-geométrica de Gauss» (PDF) . L'Enseignement Mathématique . 30 (2): 275–330. doi :10.5169/seals-53831 . Consultado el 25 de junio de 2022 . Finch, Steven R. (18 de agosto de 2003). Constantes matemáticas. Cambridge University Press. pp. 420–422. ISBN 978-0-521-81805-6
Enlaces externos "La constante de Gauss y dónde se encuentra". www.johndcook.com . 2021-10-17.