Análisis de frecuencia acumulada
Existen otras propuestas para el denominador N+1, pero éstas a la vez son consideradas incorrectas.
[3] Una manerea alternativa para calcular Pc es mediante ordenación de los datos por magnitud.
Cuando los datos X están ordenados por magnitud en una serie ascendente, primero el mínimo y al fin el máximo, y Ri es el número del rango de un cierto Xi en la serie, la probabilidad acumulada se escribe como: o en breve: Por otro lado, cuando los datos están ordenados en una secuencia descendente, primero el máximo y finalmente el mínimo, y Rj es el número de rango de un cierto Xj, la expresión de la probabilidad acumulada es: o en breve:
[4] Se puede cuestionar si la distribución de frecuencias acumuladas es utilizable para predicciones.
Por ejemplo, es que se puede predecir cuantas veces una cierta descarga de un río será sobrepasado en los años 2000 a 2050, dado una serie de descargas medidas durante los años 1950 a 2000.
La respuesta es: sí, a condición de que las circunstancias ambientales del río se cambiarán.
Aún, cuando no haya alteraciones sistemáticas, el pronóstico puede ser sujeto a un error al azar, porque las descargas obeservadas durante 1950 a 2000 por casualidad podrían haber sido mayores o menores que normal, y al contrario las descargas de 2000 a 2050 por casualidad podrán ser menores o mayores de lo normal.
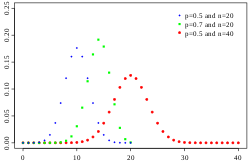
Por ello la distribución binomial se deja utilizar para estimar el intervalo de confianza.
El límite inferior (Li) y el límite superior (Ls) del intervalo de confianza de Pc bajo la condición que este tenga una distribución simétrica se calculan como: No obstante, aunque la distribución binomial es simétrica alrededor del medio (cuando Pc es 0.5), ella se vuelve más y más ladeado cuando Pc se aproxima a 0 o 1.
Por ello, el período de retorno estimado para eventos extremos está sujeto a un error al azar grande.
Además, los intervalos de confianza calculados son válidos a largo plazo.