Número real
[2] Los números reales pueden ser descritos y construidos de varias formas, algunas simples, aunque carentes del rigor necesario para los propósitos formales de las matemáticas, y otras más complejas, pero con el rigor necesario para el trabajo matemático formal.
Durante los siglos XVI y XVII, el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en aquel momento prescindían del rigor y fundamento lógico, tan exigente en los enfoques teóricos de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa.
Los números negativos fueron ideados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, pero no se utilizaron en Europa hasta el siglo XII, si bien a finales del XVIII Leonhard Euler descartó las soluciones negativas de las ecuaciones porque las consideraba irreales.
Ambos matemáticos lograron la sistematización de los números reales en la historia, no de manera espontánea, sino utilizando todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass.
En la matemática griega, dos magnitudes son conmensurables si es posible encontrar una tercera tal que las primeras dos sean múltiplos de la última, es decir, es posible encontrar una unidad común para que las dos magnitudes tengan una medida entera.
Repitiendo el proceso nuevamente se obtienen mayores números que dan una mejor aproximación.
[7] Dado que las longitudes que expresan los números irracionales podían ser obtenidas mediante procesos geométricos sencillos pero, aritméticamente, solo mediante procesos de infinitas aproximaciones, originó que durante 2000 años la teoría de los números reales fuese esencialmente geométrica, identificando los números reales con los puntos de una línea recta.
Por ejemplo, se encontraron fórmulas para resolver ecuaciones de segundo y tercer grado de forma mecánica mediante algoritmos, los cuales incluían raíces e incluso, en ocasiones, «números no reales» (lo que ahora conocemos como números complejos).
Incluso con el desarrollo de la geometría analítica este punto de vista se mantenía vigente, pues Descartes rechazaba la idea que la geometría pudiera fundamentarse en números, puesto que para él la nueva área era simplemente una herramienta para resolver problemas geométricos.
Posteriormente, la invención del cálculo abrió un período de grandes avances matemáticos, con nuevos y poderosos métodos que permitieron por vez primera atacar los problemas relacionados con lo infinito mediante el concepto de límite.
Como muestra, el número π puede estudiarse de forma algebraica (sin apelar a la intuición geométrica) mediante la serie:
Pero el análisis no contaba con definiciones rigurosas y muchas de las demostraciones apelaban aún a la intuición geométrica.
Las medidas en las ciencias físicas son siempre una aproximación a un número real.
No solo es más conciso escribirlos con forma de fracción decimal (es decir, números racionales que pueden ser escritos como proporciones, con un denominador exacto) sino que, en cualquier caso, cunde íntegramente el concepto y significado del número real.
En el análisis matemático los números reales son objeto principal de estudio.
Aun así, la escuela rusa de constructivismo supone que todos los números reales son recursivos.
, la letra "R" en negrita) para representar el conjunto de todos los números reales.
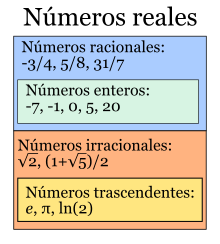
Otra forma de clasificar los números reales es en algebraicos y trascendentes.
Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario.
es un número racional, con p entero y q natural, entonces es raíz de la ecuación
[9] Se presenta una variante axiomática, mediante las siguientes tres propiedades: Un conjunto
Cualquier cuerpo ordenado que cumpla las tres propiedades mencionadas es isomorfo al conjunto de los números reales.
Los axiomas del 1 al 15 corresponden a la estructura más general de cuerpo ordenado.
y se le llama el conjunto de los números reales positivos.
y se le llama el conjunto de los números reales negativos.
[cita requerida] Tómese por ejemplo, la igualdad Es claro que esta suma opera solo con los números racionales de la forma: sin embargo, el resultado final es el número irracional
Las sucesiones de Cauchy generalizan este concepto para definir a los números reales.
Primero se define una sucesión de números racionales como una función
, en el que se puede definir una relación de orden y una topología.
EL cálculo con números reales suele llevar a resultados de numerosas cifras decimales que son inmanejables, haciéndose necesario optar por aproximaciones que introducen errores.