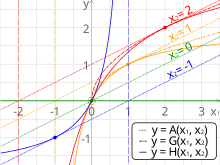
Medias pitagóricas
En matemáticas, las tres clásicas medidas pitagóricas son la media aritmética (AM), la media geométrica (GM), y la media armónica (HM).
Cada medio tiene las siguientes propiedades: Estos medios se estudiaron con proporciones en pitagóricos y posteriores generaciones de matemáticos griegos[1] debido a su importancia en la geometría y la música.
Los medios armónicos y aritméticas son duales recíprocas de uno al otro para argumentos positivos (
Mientras que la media geométrica es su propio dual recíproco.
Hay un pedido a estos medios (para todad
son todos iguales Esta es una generalización de la Desigualdad de las medias aritmética y geométrica y un caso especial de una desigualdad para las Media generalizadas.
La prueba se sigue de la desigualdad media aritmético-geométrica,
El estudio de los medios pitagóricos está estrechamente relacionado con la Mayorización y las funciones Schur-convexas.
Los medios armónicos y geométricos son funciones simétricas cóncavas de sus argumentos, y por lo tanto Schur-cóncavo, mientras que la media aritmética es una función lineal de sus argumentos, por lo que son cóncavos y convexos.