Martingala

En teoría de probabilidad, un proceso estocástico de tipo martingala (galicismo de martingale) es una secuencia de variables aleatorias en la que, en un tiempo dado, la esperanza condicional del siguiente valor de la secuencia, dado todos los valores anteriores, es igual al valor presente.El siglo XIX también se considera el nacimiento de la ruleta francesa, donde a menudo se usaba la estrategia de martingala.[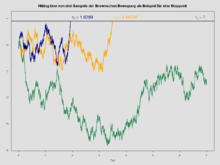1]​ La estrategia de la martingala consiste en volver a apostar por el total perdido al momento de incurrir en una pérdida en un juego de azar.En la nueva apuesta, el jugador tiene la posibilidad de recobrar todas sus pérdidas, por lo que podría parecer que a largo plazo la esperanza de ganancia con esta estrategia se mantienen constantes y a favor del jugador.De hecho, estadísticamente es así: el capital medio del jugador (esto es, el dinero que el jugador tiene a su disposición para jugar) se mantiene constante.El problema reside en que, al incurrir en sucesivas pérdidas, el jugador que siga la estrategia de la martingala se ve obligado a apostar de nuevo cantidades cada vez mayores (las pérdidas acumuladas), que tienden a crecer exponencialmente.La estrategia de la martingala se popularizó en el siglo XVIII con fama de ser una estrategia ingenua y propia de mentes simples, puesto que aunque en apariencia es infalible, está, sin embargo, abocada a arruinar al jugador.El concepto de la martingala en la teoría de probabilidades fue introducido por Paul Pierre Lévy, en 1934; el término martingala fue introducido en 1939 por Jean Ville[2]​.Una gran parte del desarrollo original de la teoría lo realizó Joseph Leo Doob; también realizó importantes contribuciones sobre aplicaciones analíticas el matemático japonés Kiyoshi Itō.El concepto fue inmediatamente aplicado al análisis de procesos bursátiles.siempre que se satisfagan los puntos siguientes: Una propiedad interesante de las martingalas es que su esperanza se mantiene constante a lo largo de todos los valores deSe adjunta una sencilla prueba a continuación:Aplicando la ley de la probabilidad total a la esperanza (también conocida como propiedad de la torre,se tiene que las martingalas poseen esperanza constante.Otras definiciones importantes (muy relacionadas con el concepto de martingala) son la sub y supermatingala.A continuación establecemos una definición para cada una de ellas.siempre que se satisfagan los puntos siguientes: Seasiempre que se satisfagan los puntos siguientes: La diferencia fundamental entre las supermartingalas y las submartingalas estriba en la dirección de la desigualdad en el segundo punto de la definición.Algunas observaciones interesantes pueden condensarse en los puntos siguientes: Notar que en las observaciones anteriores estamos abusando del lenguaje.Sea un espacio de probabilidad definido poruna sucesión de variables aleatorias que forman un proceso estocástico.Esto es, un proceso estocástico es una martingala si su esperanza en tiempo 't', consujeta a la condición de que la información conocida sobre el proceso en un instante anterior 's' sea la dada por, sea precisamente el valor que la variable aleatoria que define el proceso tomó en dicho instante 's'.Dicho de otro modo, un proceso estocástico es una martingala cuando su esperanza en tiempo futuro es precisamente el valor que la variable tiene en tiempo presente.Esto significa que el proceso no tiene deriva estadística.Cuando el mismo proceso estocástico cumple que entonces se dice que el proceso es una supermartingala.La esperanza estadística cumple la propiedad de linealidad, por lo que La esperanza estadística detodos los valores de la variable son conocidos.Así, Finalmente, un proceso estocástico se dice Browniano si la esperanza de cualquier incremento futuro es independiente de los valores presentes.