Lenia
Lenia es una familia de autómatas celulares creada por Bert Wang-Chak Chan.
[1][2][3] Lenia pretende ser una generalización continua del Juego de la vida de Conway, con estados, y espacio continuos.
la red o cuadrícula conteniendo un conjunto de estados
Este es el conjunto de estados del autómata y caracteriza los posibles estados que se pueden encontrar en cada sitio.
Muchos autómatas celulares utilizan la resolución de estado más baja posible, es decir
Lenia permite resoluciones mucho más altas.
Tenga en cuenta que el valor real en cada sitio no está en
sino más bien un múltiplo entero de
; es decir, un cuadrado de tamaño 3 centrado en cada sitio.
, que puede incluir el propio sitio original.
Tenga en cuenta que los vectores de vecindad no son la posición absoluta de los elementos, sino más bien un conjunto de posiciones relativas (deltas) con respecto a cualquier sitio determinado.
Existen variantes discretas y continuas de Lenia.
representando la posición de un sitio dado, y
Ambas variaciones comprenden dos etapas: Una vez
es calculado, se escala según la resolución de tiempo elegida
y es agregado al valor del estado original:
Aquí, la función de corte (clip) está definida por
Para Lenia discreta y continua, las reglas locales se definen de la siguiente manera:
, Chan da varias funciones que se definen radialmente .
Las funciones del kernel de ejemplo incluyen:
se utiliza para expandirlo y calcular los valores reales del kernel transformando el shell en una serie de anillos concéntricos .
, que es análogo a una función de activación, puede ser cualquier función unimodal, no monótona y que acepte parámetros
En este caso, el kernel sería rectangular, con la función
y la regla de crecimiento también rectangular, con
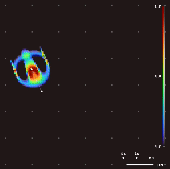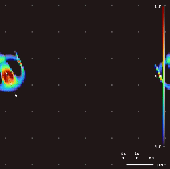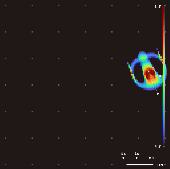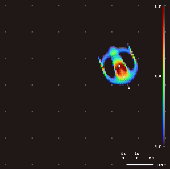
Al variar el kernel convolucional, el mapeo de crecimiento y la condición inicial, se han descubierto en Lenia más de 400 "especies" de "vida", que muestran "autoorganización, autorreparación, simetrías bilaterales y radiales, dinámica locomotora y, a veces, una naturaleza caótica".
[7] Chan ha creado una taxonomía para estos patrones.
[1] Otros trabajos han notado la gran similitud entre las reglas de actualización de los autómatas celulares y las convoluciones.
De hecho, estos trabajos se han centrado en la reproducción de autómatas celulares utilizando redes neuronales convolucionales simplificadas.
[9] Gilpin descubrió que cualquier autómata celular podría representarse como una red neuronal convolucional y entrenó redes neuronales para reproducir autómatas celulares existentes [8] Desde este punto de vista, los autómatas celulares pueden verse como un caso especial de redes neuronales convolucionales recurrentes .
Sin embargo, Lenia utiliza kernels fijos mucho más grandes y no se entrenan mediante el descenso de gradiente.